Research
Vertical-Mode Decomposition under Nonlinear and Topographic Effects
Motivation
Vertical modes are one of the standard tools to analyze stratified flows. They are calculated from background stratification assuming hydrostatic linear flows over flat bottom. However, they have been applied to field-data analysis despite the assumptions, as well as theoretical studies of weakly nonlinear and nonhydrostatic flows4),5) over mild slopes7),8) using the perturbation method. Furthermore, they are more recently found to be useful for developing fully-nonlinear internal-wave theories (see Fully-nonlinear Simple Internal Waves). My aim was to extend the theory of vertical modes to allow nonlinear and topographic effects.
Approach
The main advantage of vertical modes is that they are often efficient in describing the vertical structure of flows in oceans and lakes. Under the assumptions of hydrostaticity, linearity, and flat bottom, individual vertical modes follow decoupled equations equivalent to the shallow-water equations1),6). My idea was to extend this to include large topographic effects by defining vertical modes using the local water depth (hence vertical modes become spatially variable). We can still decompose the governing equations into individual modal components but with additional topographic interaction terms.
While I worked on the linear version of the theory, I became aware that Griffiths and Grimshaw2) previously used this approach for linear flows, so the originality of the idea goes back to their study (to my knowledge). I also became aware that Sam M. Kelly and coworkers3) independently worked on the same idea for linear flows around the same time as my study. My formulation has advantages in its simpler and more general form, which allowed a later extension of the idea to fully nonlinear cases.
Theory
I initially presented the linear, multi-layer stratification version of the theory in Shimizu (2011), but the theory has been extended to full nonlinearity in continuously stratified fluids in Shimizu (2019). The fully nonlinear version of the theory is briefly presented below.
We assume stably stratified flows in shallow water, and neglect the Coriolis effect. We assume variable water depth $H(x)$, and horizontally uniform background stratification with the density profile $\rho_{\text{ref}}(z)$. My formulation uses a generalized isopycnal coordinate, but the equations below are written using the height of undisturbed isopycnals $Z$, so that the equations are similar to those in the standard height ($z$) coordinate.
Vertical modes for vertical motion, $\phi_n(x, Z)$, are defined in the standard way1) except the use of the undisturbed height $Z$:
\begin{align} c_n^2 \frac{d}{dZ} \left( \rho \frac{d\phi_n}{dZ} \right)+&\rho N^2 \phi_n = 0, \\ c_n^2 \frac{d\phi_n}{dZ}=g \phi_n \quad &\text{at} \quad Z=0, \\ \phi_n=0 \quad &\text{at} \quad Z=-H(x), \end{align}where $N(Z)$ is the buoyancy frequency, $c_n(x)$ is the celerity, and the subscript $n$ is the modal index. We also introduce vertical modes for horizontal motion, $\pi_n(x, Z)$ through
\begin{align} \pi_n = h_n \frac{d\phi_n}{dZ}, \end{align}where $h_n(x)$ is an arbitrary normalization factor of $n$th mode with the unit of water depth. Using the above vertical modes, we can project the isopycnal displacement $\eta$ and horizontal velocity $u$ as
\begin{align} \eta(x,Z,t)&= \sum_n \phi_n(x,Z) \eta_n(x,t), \\ u(x,Z,t) &= \sum_n \pi_n(x,Z) u_n(x,t). \\ \end{align}Using the above modal expansion and the orthogonality of vertical modes, we can decompose the governing equations into modal components. The resulting evolutionary equations for individual vertical modes with 2nd-order (moderately strong) topographic effects are
\begin{align} \underline{\frac{\partial \eta_n}{\partial t}} = &\underline{-\frac{\partial}{\partial x} \left( \left( h_n \delta_{nm} + \epsilon N_{mln} \eta_l \right) u_m \right)} \\ & + \delta \left( L_{mn} h_m + \epsilon M_{mln} \eta_l \right) u_m - \delta \left( B^L_{mn} + \epsilon B^M_{mln} \frac{\eta_l}{h_l} \right) u_m - \delta \frac{\rho^b}{\hat{\rho}} \pi_n^b \frac{\partial \eta_B}{\partial t}, \\ \underline{\frac{\partial u_n}{\partial t}} =& \underline{-\frac{\partial}{\partial x} \left( \frac{c_n^2}{h_n} \eta_n \right) - \epsilon N_{lnm} u_l \frac{\partial u_m}{\partial x}} \\ & - \delta \left( L_{nm} \frac{c_m^2}{h_m} \eta_m + \epsilon M_{lnm} u_l u_m \right), \\ \frac{\partial \eta_B}{\partial t} =& - \epsilon \frac{\partial}{\partial x} \left( \pi_m^b u_m \eta_B \right) - \left( 1 + \epsilon \pi_l^b \frac{\eta_l}{h_l} \right) \pi_m^b u_m \theta, \\ \end{align}where the sums on $l$ and $m$ are assumed, $\eta_B$ is effectively the isopycnal displacement at the bottom, $\theta(x)$ is the bottom slope, $\hat{\rho}$ is a constant reference density, and the superscript $b$ indicates the value at the bottom. Dimensionless parameters $\epsilon$ and $\delta$ indicate the magnitudes of nonlinear and topographic effects, respectively. In the above equations, the following variables are modal interaction coefficients defined as
\begin{align} N_{nlm}&=\frac{1}{\hat{\rho} h_l} \int_{-H}^{0} {\rho \pi_n \pi_l \pi_m dZ}, \\ L_{nm}&=\frac{1}{\hat{\rho} h_n} \int_{-H}^{0} {\rho \pi_n \frac{\partial \pi_m}{\partial x} dZ}, \\ M_{nlm}&=\frac{1}{\hat{\rho} h_l} \int_{-H}^{0} {\rho \pi_n \pi_l \frac{\partial \pi_m}{\partial x} dZ}, \\ B^L_{nm}&= \frac{\rho^b}{\hat{\rho}} \pi^b_n \pi^b_m \theta, \\ B^M_{nlm}&= \frac{\rho^b}{\hat{\rho}} \pi^b_n \pi^b_l \pi^b_m \theta. \end{align}From the top, they represent interactions due to the advection of horizontal momentum and isopycnal heaving, linear and nonlinear topographic effects, and linear and nonlinear effects of varying bottom boundary density, respectively. Setting $\epsilon=\delta=0$ yields equations equivalent to the shallow water equations for individual vertical modes, and $\delta=0$ recovers the fully-nonlinear version for flat bottom used in Shimizu (2017). The assumption of small $\delta$ becomes unnecessary for linear problems, and setting $\epsilon=0$ conveniently recovers the linear, steep-slope version of the theory in Shimizu (2011).
Applications
The above fully nonlinear theory forms the basis for the theory of topography-modified simple internal waves (see here). This is because it was essential to separate so-called "adiabatic" (or conservative) and "diabatic" processes, and the above theory provides a convenient way of separating different physical processes. For example, the underlined terms in the above equations are the adiabatic terms.
As an example application in which the total water-depth change is large, I applied the theory to Wunsch's subcritical wedge problem9) (Fig. 1). The problem is linear, but large water-depth change and the existence of an analytic solution make it an important example application. The solution to this problem based on the above theory has the form
\begin{align} u_n = A_n (\theta x)^{\text{i} \gamma} \text{exp}(- \text{i} \omega t), \end{align}where the exponent $\gamma$ needs to be determined numerically. This semi-analytic solution converges to the Wunsch's analytic solution as more vertical modes are included in the calculation. They are compared to topography-modified simple-wave solutions with 1st- (weak) and 2nd-order (moderately strong) topographic effects in Fig. 1.
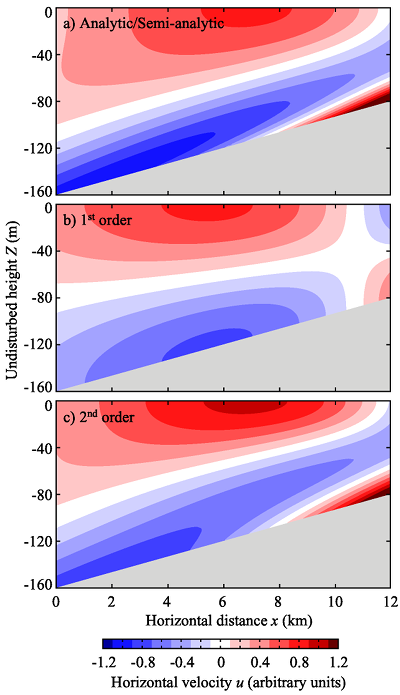
Fig. 1. Horizontal velocity fields of linear solutions under linear stratification and bottom slope of 0.0066. (a) Wunsch's analytic solution or semi-analytic solution based on the above theory, and topography-modified simple-wave solutions with (b) 1st-order and (c) 2nd-order topographic effects.
Related Publications
The linear, multi-layer stratification version of the theory was presented in
Details of the topography-modified simple-wave solution are available in
The fully nonlinear and nonhydrostatic but flat-bottom version of the theory is available in
Acknowledgements
The early ideas and the theory for this study were developed while I was studying at Centre for Water Research, University of Western Australia, with the financial support of Japanese government (MEXT) scholarship and Tokyo Tech Long-Term Study Support Program.
References
- Gill, A. E. 1982. Atmosphere–Ocean Dynamics. Academic Press, 662 pp.
- Griffiths, S. D., and R. H. J. Grimshaw. 2007. Internal tide generation at the continental shelf modeled using a modal decomposition: Two-dimensional results. Journal of Physical Oceanography, 37: 428–451.
- Kelly, S. M., J. D. Nash, K. I. Martini, M. H. Alford, and E. Kunze. 2012. The cascade of tidal energy from low to high modes on a continental slope. Journal of Physical Oceanography, 42: 1217-1232.
- Lamb, K. G., and L. Yan, 1996. The evolution of internal wave undular bores: Comparisons with a fully nonlinear numerical model with weakly nonlinear theory. Journal of Physical Oceanography, 26: 2712–2734.
- Lee, C.-Y., and R. C. Beardsley. 1974. The generation of long nonlinear internal waves in a weakly stratified shear flow. Journal of Geophysical Research - Oceans, 79: 453–462.
- Lighthill, M. J. 1969. Dynamic response of the Indian Ocean to onset of the southwest monsoon. Philosophical Transactions of Royal Society of London, 265A: 45–92.
- Llewellyn-Smith, S. G., and W. R. Young, 2002. Conversion of the barotropic tide. Journal of Physical Oceanography, 32: 1554–1566.
- Maugé, R., and T. Gerkema. 2008: Generation of weakly nonlinear nonhydrostatic internal tides over large topography: A multi-modal approach. Nonlinear Processes in Geophysics, 15: 233–244.
- Wunsch, C. 1969. Progressive internal waves on slopes. Journal of Fluid Mechanics, 35, 131-144.