Research
Fully-nonlinear Simple Internal Waves
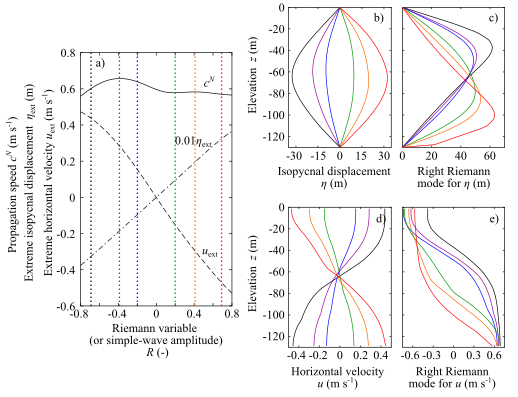
Fig.1. Semi-analytic solution for 1st-baroclinic-mode right-propagating simple internal wave and associated Riemann modes. (a) Nonlinear propagation speed, and extreme (minimum or maximum) isopycnal displacement and horizontal velocity over water column; and selected (b,c) isopycnal-displacement and (d,e) horizontal-velocity profiles and corresponding right Riemann modes. Line colour in panel (b-e) corresponds to a dotted line with the same colour in panel (a).
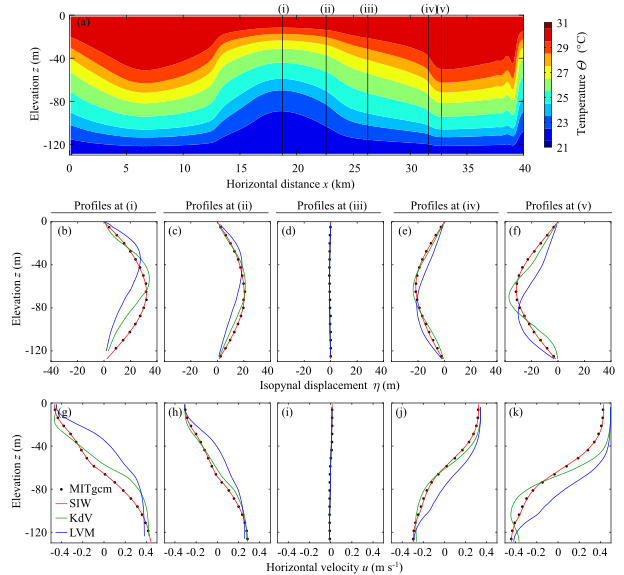
Fig.2. Comparisons of MITgcm outputs and (semi-) analytic solutions. (a) Temperature cross-section from MITgcm, and comparisons of (b-f) isopycnal-displacement and (g-k) horizontal-velocity profiles at locations indicated by vertical lines in panel (a). Abbreviations are SIW: simple-internal-wave theory, KdV: 2nd-order KdV theory, and LVM: linear vertical-mode theory.
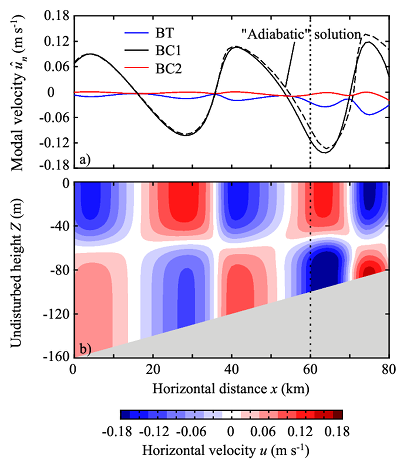
Fig. 3. Fully nonlinear simple-wave solution with 2nd-order topographic effects under hyperbolic-tangent stratification and uniform bottom slope of 0.001. (a) Modal velocities of the barotropic (BT), 1st baroclinic (BC1), and 2nd baroclinic (BC2) modes, and (b) horizontal velocity field. Dashed line in (a) shows adiabatic solution for BC1.
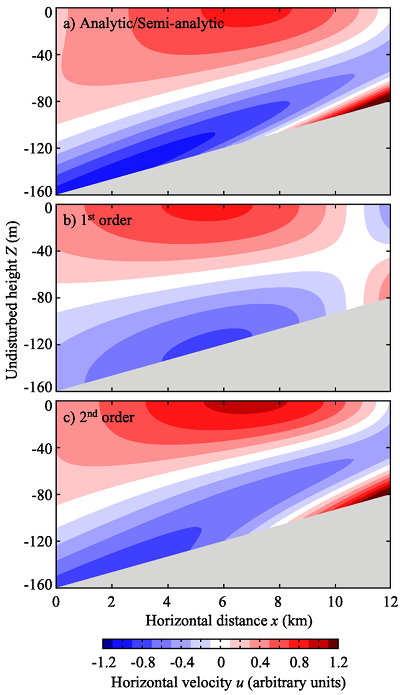
Fig. 4. Horizontal velocity fields of linear solutions under linear stratification and bottom slope of 0.0066. (a) Analytic solution, and perturbation solutions with (b) 1st-order and (c) 2nd-order topographic effects.
Motivation
The theory of fully-nonlinear, one-directional, non-dispersive waves, called simple waves, provides an important basis to understand fully-nonlinear waves in various fields of physics and engineering2,4,5). However, simple-wave solution was not available for internal waves in continuously stratified fluids. Furthermore, the solution has several bottlenecks for realistic geophysical application, and one of them was the lack of topographic effects. I have derived semi-analytic fully-nonlinear simple-wave solution for internal waves under continuous stratification, and extended it to include 2nd-order (moderately strong) topographic effects.
Theory
The theory was developed based on vertical-mode decomposition of the governing equations in the presence of bottom slopes (see Vertical Mode Decomposition under Nonlinear and Topographic Effects). As a first step, I developed the simple-internal-wave theory over flat bottom in Shimizu (2017). Similar to the well-known vertical modes1), the simple-internal-wave solution provides the propagation speed $c^N$ and the associated vertical structure (right Riemann mode) of fully-nonlinear internal waves. The solution can be calculated semi-analytically using the power-series solution. Then, the horizontally and temporally varying amplitude (Riemann variable or invariant) $R$ follows the wave-propagation equation \begin{align} \left( \frac{\partial}{\partial t} + c^N \frac{\partial}{\partial t} \right) R = 0. \\ \end{align} As for simple waves in other fields of physics2,5), $R$ remains constant along the characteristic (or propagation path) $dx/dt = c^N$.
As a second step, I developed a theory of fully-nonlinear simple internal waves with 2nd-order topographic effects. This was done by using the perturbation method to add so-called "diabatic" (non-conservative) topographic adjustments to "adiabatic" (conservative) simple-internal-wave solution over a mild slope (Shimizu, 2019). After extending the definition of Riemann variable $R$ so that it remains constant under adiabatic topographic effects, the governing equations are \begin{align} \left( \frac{\partial}{\partial t} + c^N \frac{\partial}{\partial t} \right) R = S_R, \\ \left( \frac{\partial}{\partial t} + u^b \frac{\partial}{\partial t} \right) \eta_B = S_{\eta}, \end{align} where $\eta_B$ is effectively the isopycnal displacement at the bottom, $u^b(R, \eta_B)$ is the near-bottom horizontal velocity, and $S_R(R, \eta_B)$ and $S_{\eta}(R, \eta_B)$ are diabatic source terms due to topographic effects. Now, the Riemann variable $R$ varies along the characteristic because of diabatic effects (topographic interaction with other modes). An important feature of the theory is the applicability to large water-depth change over a long distance, provided that the local bottom slopes are mild.
Results
For illustration purposes, the flat-bottom simple-internal-wave solution was compared to numerical simulations using MITgcm3), linear vertical-mode theory, and 2nd-order Korteweg-de Vries (KdV) theory, which includes moderately strong nonlinearity. The stratification was taken from observations on Australian North West Shelf. Fig. 1 shows the semi-analytic simple-internal-wave solution. The small amplitude limit ($R\sim0$) corresponds to the linear vertical-mode theory. Fig. 2 show the comparisons of the (semi-)analytic and numerical solutions. The linear and 2nd-order KdV theories deviate from the fully nonlinear solution beyond roughly 20-m (semi-)amplitude. The agreement of simple-internal-wave solution and the MITgcm outputs shows that MITgcm is capable of simulating the propagation of fully nonlinear internal waves.
Fig. 3 shows an example of simple internal waves for a very mild slope under hyperbolic-tangent stratification. The adiabatic part of the solution provides a good first approximation to the wave field, but the diabatic adjustments become substantial as waves shoal. The separation of adiabatic part allows the application to relatively large water-depth change (160 m to 80 m in this example), because the Riemann variable $R$ remains constant under adiabatic topographic effects.
Fig. 4 shows an example for a relatively steep slope under linear stratification. Linear solutions with 1st- (weak) and 2nd-order (moderately strong) topographic effects are compared to the analytic solution to the Wunsch's subcritical wedge problem6). Since the bottom slope is 2/3 of the propagation angle of internal wave rays (so-called critical angle), a beam-like structure (blue patch) is apparent in the analytic solution. The 1st-order topographic effects fail to reproduce feature, but the 2nd-order topographic effects capture the essential features of the solution. This illustrates that the theory is applicable to subcritical slopes, much steeper slopes than those initially assumed in the perturbation method.
Discussion
To my knowledge, my studies were the first to derive the theory and solution for fully-nonlinear simple internal waves over flat bottom, and then to incorporate topographic effects. More generally, the theory might be novel as a theory of fully-nonlinear simple waves in a gradually varying cross-section, although comprehensive literature survey is difficult because there are vast fields of physics in which the simple-wave theory can be applied.
The proposed simple-internal-wave solution provides a generic new tool that can be used for many purposes, such as the analysis of field and model data, and numerical model set-up. There are still a few bottlenecks for the application of fully nonlinear internal-wave theory to internal waves in realistic geophysical application, such as the lack of the Coriolis effect and horizontal two-dimensionality. I plan to tackle these problems in the future.
Related Publications
Details of the flat-bottom simple-internal-wave solution are available in
Details of the topography-modified simple-internal-wave solution are available in
Comparisons with MITgcm and other theories are presented in
References
- Gill, A. E. 1982. Atmosphere-Ocean dynamics. Academic Press.
- Lighthill, J. 1978. Waves in fluids. Cambridge University Press.
- Marshall, J., A. Adcroft, C. Hill, L. Perelman, and C. Heisey. 1997. A finite-volume, incompressible Navier-Stokes model for studies of the ocean on parallel computers. Journal of Geophysical Research - Oceans, 102: 5753–5766.
- Ostrovsky, L. A., and J. Grue. 2003. Evolution equations for strongly nonlinear internal waves, Physics of Fluids, 15, 2934-2948.
- Whitham, G. B. 1974. Linear and nonlinear waves. Wiley.
- Wunsch, C. 1969. Progressive internal waves on slopes. Journal of Fluid Mechanics, 35, 131-144.