Research
Fully-nonlinear Ekman-layer solution and its application to Tokyo Bay

Fig. 1. Schematics of Ekman and nonlinear pumping under negative wind stress curl (in Northern Hemisphere).
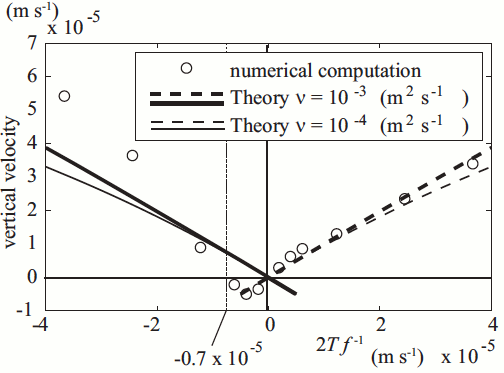
Fig. 2. Comparison of theoretical fully-nonlinear Ekman layer solutions with idealized numerical simulations in a cylindrical basin under spatially uniform wind stress curl. Horizontal axis is wind stress curl normalized by water density and Coriolis parameter (i.e., Ekman pumping velocity for linear Ekman layer), and vertical axis is vertical velocity at the base of surface Ekman layer. Dashed and solid lines indicate the first and second branches, respectively. Taken from Nakayama et al. (2014, J. Geophys. Res.)
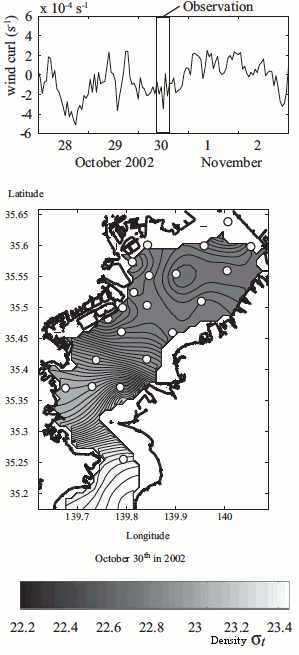
Fig. 3. Field observations of wind-driven downwelling in Tokyo Bay on 28 October 2002. Top panel shows low-pass filtered wind curl with a cut-off period of 24 h. Bottom panel shows water density at 10 m depth. Taken from Nakayama et al. (2014, J. Geophys. Res.)
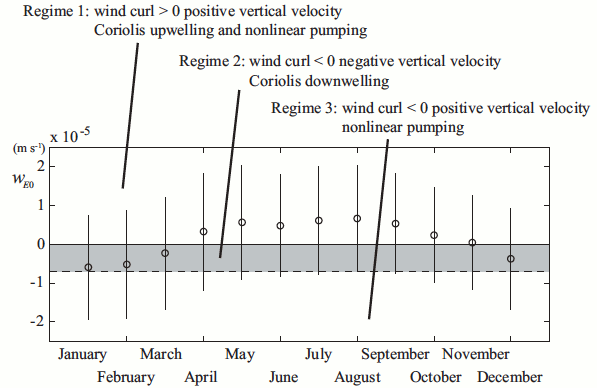
Fig. 4. Monthly statistics of wind stress curl normalized by water density and Coriolis parameter over the head of Tokyo Bay. Circles and bars indicate monthly average and one standard deviation, respectively. Taken from Nakayama et al. (2014, J. Geophys. Res.)
Introduction
Wind-driven upwelling is important for the water quality and ecology in coastal zone. The traditional spin-up theory tells that wind stress curl determines the sign of vertical velocity at the base of the surface boundary layer, or Ekman layer. However, during their study of horizontal and residual circulation in Tokyo Bay, my collaborators, Prof. Keisuke Nakayama at Kobe Uni. and Dr. Tetsuya Shintani at Tokyo Metropolitan Uni., came up with an idea that the centrifugal force can induces upwelling regardless of the sign of wind stress curl (Fig. 1). I was asked to investigate the effects of strong nonlinearity in the surface Ekman layer from a theoretical perspective. Previous studies in oceanography considered only the traditional Ekman downwelling under weak2),4),6-7) and strong1),3) anti-cyclonic forcing (i.e., negative, or clockwise, wind stress curl in Northern Hemisphere).
Fully-nonlinear Ekman layer solution
Following previous studies on the von Karman swirling flow problem5),8), we numerically solved a set of ordinary differential equations for fully-nonlinear (steady) Ekman layer. We imposed wind stress curl at the surface and a slip condition at the base, which approximates reduced mixing (eddy viscosity) due to stratification.
There are two important branches of the solution, one corresponding to the traditional Ekman layer, and the other corresponding to upwelling under anti-cyclonic forcing. Numerical solutions in an idealized cylindrical basin under spatially uniform wind stress curl suggests bifurcation from the first to second branch (Fig. 2). The second branch appears to be physically realisable only under strong anti-cyclonic forcing, when the centrifugal force exceeds the Coriolis force. This suggests the following three Regimes in nonlinear surface Ekman layer:
- Ekman and nonlinear upwelling under cyclonic forcing (positive wind stress curl in Northern Hemisphere)
- Ekman downwelling under weak anti-cyclonic forcing
- Nonlinear upwelling under strong anti-cyclonic forcing
The idealized numerical simulations suggest that the threshold between Regimes 2 and 3 is $(\nabla \times \vec{\tau})/(\rho f) \approx -7 \times 10^{-6} \text{(m/s)}$, where $\vec{\tau}$ is the wind stress vector, $\rho$ is the water density, and $f$ is the Coriolis parameter.
Application to Tokyo Bay
Tokyo Bay is an semi-enclosed bay with a length and width of about 60 and 15 km, respectively. The depth changes sharply from a few hundreds of meters at the bay mouth to 15 m at the bay head. Fig. 3 shows an example of observed downwelling under weak anti-cyclonic forcing.
Statistics of wind stress curl over Tokyo Bay shows that anti-cyclonic forcing is strong enough to induce nonlinear upwelling in winter (Fig. 4). However, time-dependent numerical simulations show that it takes approximately an inertial period (~18 h in Tokyo Bay) for an Ekman layer to induce nonlinear upwelling under anti-cyclonic forcing. Since typical duration of anti-cyclonic forcing over Tokyo Bay is less than ~6 h, Regimes 3 would occur only under exceptional conditions.
Implications to other sites
The magnitude of wind stress curl over Tokyo bay, O(10-6 N/m3), is an order of magnitude larger than over Great Lakes or open ocean, O(10-7 N/m3), which is probably due to orographic effects. It implies that strongly nonlinear Ekman layer is relevant to medium-sized bays and lakes surrounded by complex terrain.
Related Publications
Details are available in
Acknowledgements
This work was supported by the Japan Society for the Promotion of Science. I appreciates the financial support from the Max Planck Society for the Advancement of Science through the Klaus Hasselmann Postdoctoral Fellowship during the write-up of the above paper.
References
- Benton, G. S., F. B. Lipps, and S. Y. Tuann. 1964. The structure of the Ekman layer for geostrophic flows with lateral shear. Tellus, 16: 186–199.
- Brink, K. H. 1997. Time-dependent motions and the nonlinear bottom Ekman layer. Journal of Marine Research, 55: 613–631.
- Hart, J. E. 2000. A note on nonlinear corrections to the Ekman layer pumping velocity. Physics of Fluids, 12: 131–135.
- Pedlosky, J. 2008. On the weakly nonlinear Ekman layer: Thickness and flux. Journal of Physical Oceanography, 38: 1334–1339.
- Rogers, M. H., and G. N. Lance. 1960. The rotationally symmetric flow of a viscous fluid in the presence of an infinite rotating disk. Journal of Fluid Mechanics, 7: 617–631.
- Stern, M. E. 1965. Interaction of a uniform wind stress curl with a geostrophic vortex. Deep Sea Research Oceanographic Abstrast, 12: 355–367.
- Thomas, L. N., and P. B. Rhines. 2002. Nonlinear stratified spin-up. Journal of Fluid Mechanics, 473: 211–244.
- Zandbergen, P. J., and D. Dijkstra. 1987. Von Karman swirling flows. Annual Review of Fluid Mechanics, 19: 465–491.