Research

Damping Mechanisms of Internal Waves in Continuously Stratified Rotating Basins

Fig. 1. Bottom-corner region in a linearly stratified rotating circular basin. (a) Schematics of a circular basin and the definition of variables, and b,c) flow field under fundamental-mode internal Kelvin wave with $S=0.3$ and Poincaré wave with $S=1.0$, respectively. $E/S=3 \times 10^{−3}$ is used for plotting. In the inviscid limit, no radial and vertical velocities are induced at the phase shown, and the azimuthal velocities above the bottom boundary layer are into the display. Blue lines indicate the angle of internal-wave ray, with the vertical distance corresponding to the bottom-boundary-layer thickness $\Delta_z$. Modified from a figure in Shimizu and Imberger (2009, J. Fluid Mech.).

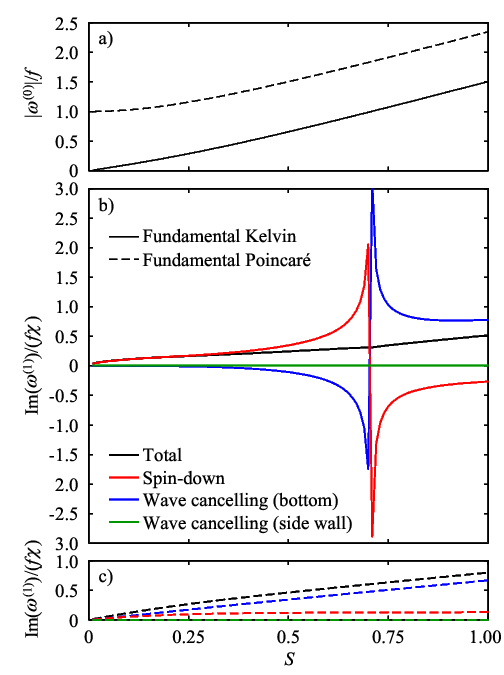
Fig. 2. Dispersion relationships and damping rates of fundamental-mode internal Kelvin and Poincaré waves in a circular basin. Coloured lines show contributions of different mechanisms. $\chi$ is a non-dimensional factor that depends on the vertical mode of interest, and $\chi \approx 2$ for vertical mode 1 under linear stratification and the Boussinesq approximation. Modified from a figure in Shimizu and Imberger (2009, J. Fluid Mech.).

Fig. 3. Horizontal structure of fundamental-mode internal Kelvin and Poincaré waves. (1st row): weakly viscous solution, (2nd row): inviscid solution, and (3rd-5th row) 1st-order correction due to spin-down, internal wave cancelling by bottom friction, and that by side wall friction, respectively. Colour shading and vector show isopycnal displacements and horizontal velocities, respectively, at $z/H=−0.75$. Isopycnal displacements $\eta$ and horizontal velocity $\vec{v}$ are respectively scaled by $a$ and $ca/R$, where $a$ is the maximum isopycnal displacement. Weakly viscous solution (top) is given by $\xi=\xi^{(0)}+(E/S)^{1/2} \left( \xi_{sp}^{(1)} + \xi_{iwc}^{(1)} + (H/R) \xi_{sw}^{(1)} \right)$, where $\xi=\eta, \vec{v}$. $E/S=0.08$ is used for plotting. Modified from a figure in Shimizu and Imberger (2009, J. Fluid Mech.).

Motivation

In our study on the damping of basin-scale internal waves in Lake Kinneret, we found that the waves are damped within a few days in a 40-m-deep lake by bottom friction. When we got this result, my PhD supervisor, Jörg Imberger, asked me how this is possible, because the momentum or energy loss within the boundary layer cannot diffuse into the interior so rapidly. It turned out that this was an unsolved problem for gravity waves under the Coriolis effect. The answer to this question is essential to model damping of internal waves in a physically plausible way.

Approach

Our approach was to solve the problem analytically using a singular perturbation method by combining the following limiting cases:

  • The well-known spin-down problem of low-frequency motions (compared to the inertial frequency) under the Coriolis effect3),5); and
  • The damping of progressive gravity waves without the Coriolis effect, which is probably not well-known but have been solved originally (to my knowledge) by Johns (1968).

Conveniently, these processes could be combined in a singular perturbation theory because both of them occur through boundary-normal velocity (or unsteady Ekman pumping velocity), which is induced by the divergence of volume-transport deficit due to boundary friction (or unsteady Ekman transport). Note, however, that the processes within the interior are different in the two cases.

  • In spin-down, boundary-normal velocity excites quasi-geostrophic currents, through the conservation of potential vorticity, that counteracts against the existing interior flow.
  • In gravity wave damping, boundary-normal velocity excites additional gravity waves, through processes similar to the lee-wave generation, that partly cancel the existing wave. This process is called (internal) wave cancelling in this study.

These damping processes are much faster than diffusional damping because the damping of the interior flow occurs through inviscid processes.

In addition to the two known cases, solving the problem required two additional processes: side-wall boundary layer, induces additional wave-cancelling process, and Boundary-layer/interior flow communication in the bottom corner region.

Results

To derive an analytic solution, we considered a rotating, linearly stratified basin with cylindrical shape and flat bottom. Schematics of the problem and the definition of variables are shown in Fig. 1a. The solution is written in a perturbation expansion of the form:

\begin{align} \xi=\xi^{(0)}&+(E/S)^{1/2}\xi^{(1)}+\cdots,\\ E&=\frac{\nu}{fH^2},\\ S&=\frac{c}{fR}, \end{align}

where $\xi=\omega, \eta, \vec{v}$, $E$ is the Ekman number, $S$ is the Burger number 1), $\omega$ is the complex-valued angular frequency (the imaginary part represents the damping rate), $c$ is the celerity of the vertical mode of interest, and $\nu$ is the kinematic viscosity. We use $H/R=0.01$ in our examples.

Zoom-up of the solution in the bottom corner region is shown in Fig. 1b,c. Bottom friction creates the bottom boundary layer (grey shading) and the side-wall boundary layer (too thin to be seen in the figure), which modify the interior flow from the inviscid solution. Note that the boundary layer flow has a transverse component to the left of the interior flow when $\omega/f < 1$, but to the right when $\omega/f > 1$. Note also that the discontinuity of the Ekman transport at the bottom corner induces a corner jet when $\omega/f \ll 1$2),7), but an internal wave beam when $\omega/f \approx 1$. As a result, the contributions of different processes change rapidly near $\omega/f = 1$ (Fig. 2b).

Damping rates and horizontal structure of the fundamental-mode (i.e., vertical mode 1, radial mode 1, azimuthal mode 1) internal Kelvin and Poincaré waves are illustrated in Fig. 2 and Fig. 3.

Application to Lake Kinneret
The analytic solution for a circular basin was applied to Lake Kinneret. Using typical stratification in summer and eddy viscosity in the bottom boundary layer ($E \approx 1.4 \times 10^{−3}$ and $S \approx 0.6$), the e-folding damping times of the fundamental-mode Kelvin and Poincaré waves were estimated to be ~6 and ~3 days, respectively. These numbers were comparable to the estimates from field data (~2 and ~1 days, respectively). This encouraging result led us to a separate study, which included the damping mechanisms considered here into the numerical scheme of modal analysis. By taking bottom friction and realistic bathymetry into account, we were able to predict the observed damping rates in Lake Kinneret (see Modal analysis - Lake Kinneret).
Related Publications

Details are available in

Shimizu, K., and J. Imberger. 2009. Damping mechanisms of internal waves in a continuously-stratified rotating basin. Journal of Fluid Mechanics, 637: 137-172. doi:10.1017/S0022112009008039.

Acknowledgements

This study was conducted when I was a PhD candidate at Centre for Water Research, University of Western Australia, with financial support of Japanese government (MEXT) scholarship and Tokyo-Tech Long-term Overseas Study Support Program.

References
  1. Antenucci, J. P., and J. Imberger. 2001. Energetics of long internal gravity waves in large lakes. Limnology and Oceanography, 46: 1760–1773.
  2. Duck, P. W., and M. R. Foster. 2001. Spin-up of homogeneous and stratified fluid. Annual Review of Fluid Mechanics, 33: 231–263.
  3. Greenspan, H. P. 1968. Theory of Rotating Fluid. Cambridge University Press.
  4. Johns, B. 1968. A boundary layer method for the determination of the viscous damping of small amplitude gravity waves. Quarterly Journal of Mechanics and Applied Mathematics, 21: 93–103.
  5. Pedlosky, J. 1979. Geophysical Fluid Dynamics. Springer.
  6. Shimizu, K., and J. Imberger. 2009. Damping mechanisms of internal waves in a continuously-stratified rotating basin. Journal of Fluid Mechanics, 637: 137-172.
  7. Walin, G. 1969. Some aspects of time-dependent motion of a stratified rotating fluid. Journal of Fluid Mechanics, 36: 289–307.

© 2017-2024 Kenji Shimizu