Research
Oblique Interaction of Internal Solitary-like Waves (or Solitons) in the Andaman Sea
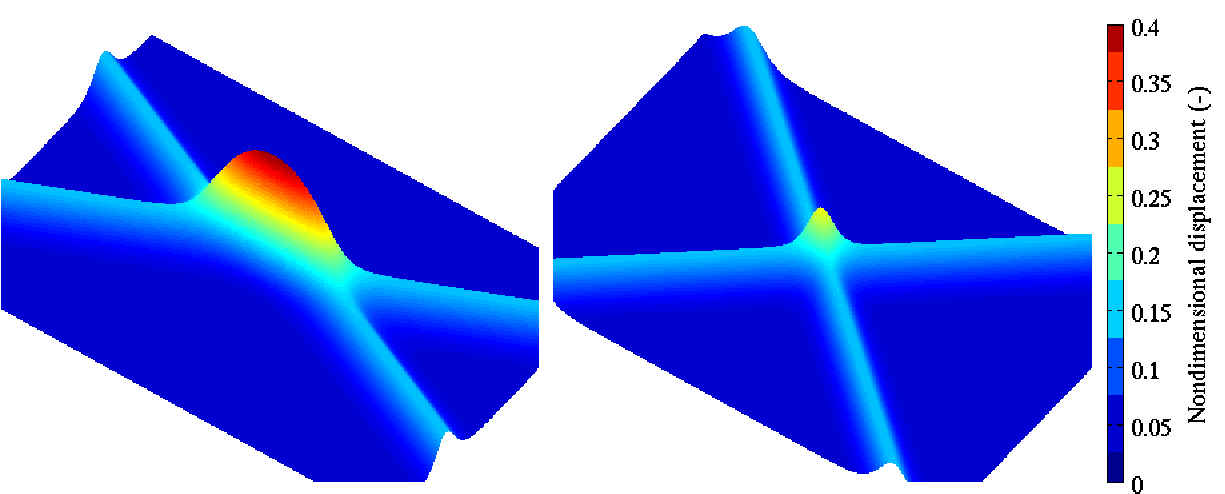
Fig. 1. A bird's-eye-view of obliquely interacting solitary waves (left) with and (right) without nonlinear amplitude enhancement.
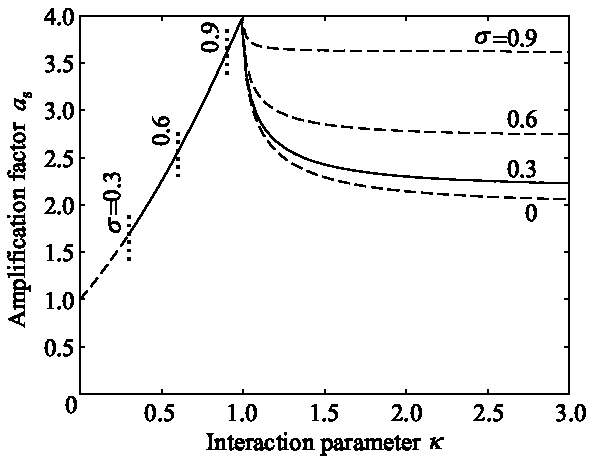
Fig. 2. Relationship between extended Miles interaction parameter $\kappa$ and amplification factor $a_s$. Solid line shows relationship for $\sigma$=0.3, and dashed lines for $\sigma$=0.0, 0.6, and 0.9. Vertical dotted lines indicate lower limit of applicable $\kappa$ for given $\sigma$. Figure taken from Shimizu and Nakayama (2017, J. Geophys. Res.-Oceans).
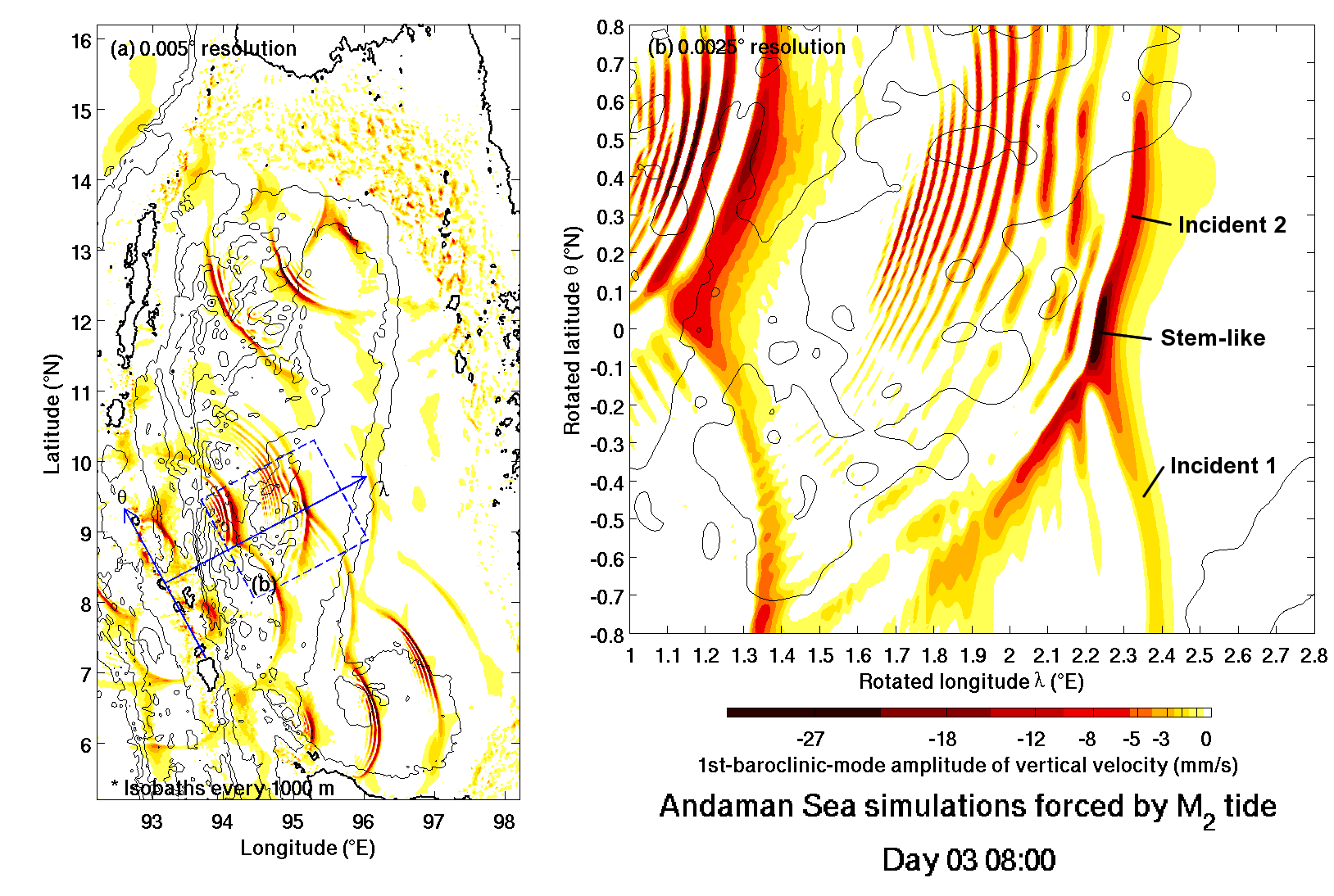
Fig. 3. A snapshot of modelled vertical velocity in the Andaman Sea (Full Coriolis case). (a) Model output from 0.005° grid, and (b) that from 0.0025° grid in region of interest, shown in rotated coordinates defined in (a). Note that only negative velocity is shown and that colour scale is nonlinear. Click image to see the movie (1.9MB, not for small screen).
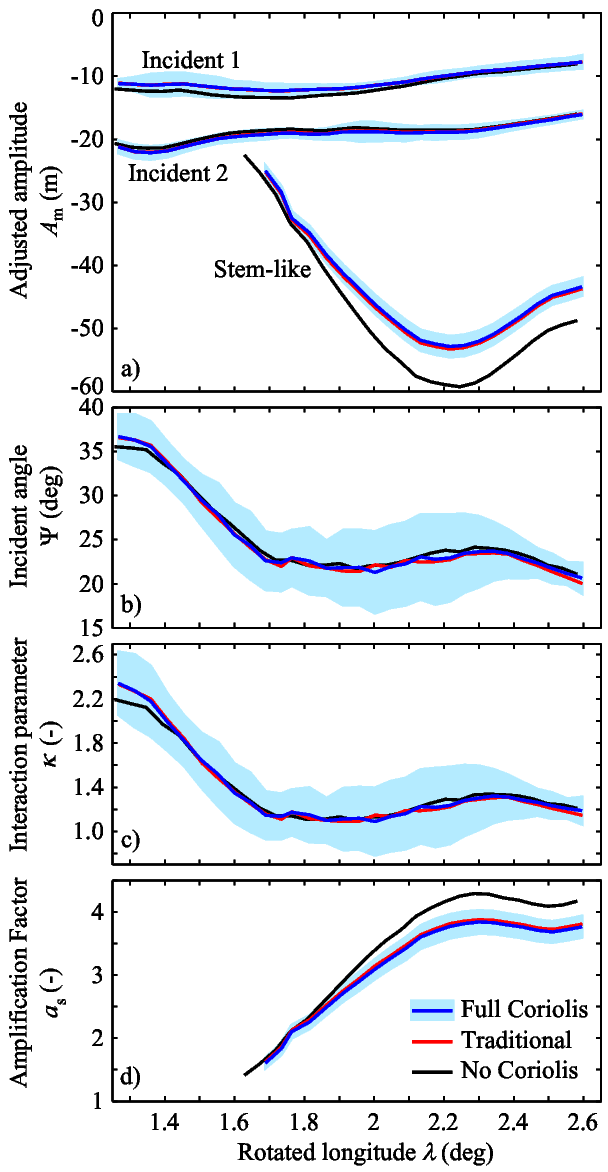
Fig. 4. Parameters relevant to oblique ISW interaction. (a) Amplitudes of incident and stem-like ISWs, (b) incident angle, (c) extended Miles interaction parameter, and (d) amplification factor. Note that we use negative amplitude for ISW of depression. Shading indicates uncertainty in Full Coriolis case. Uncertainties in Traditional and No Coriolis cases are similar to Full Coriolis case. Reformatted from Shimizu and Nakayama (2017, J. Geophys. Res.-Oceans).
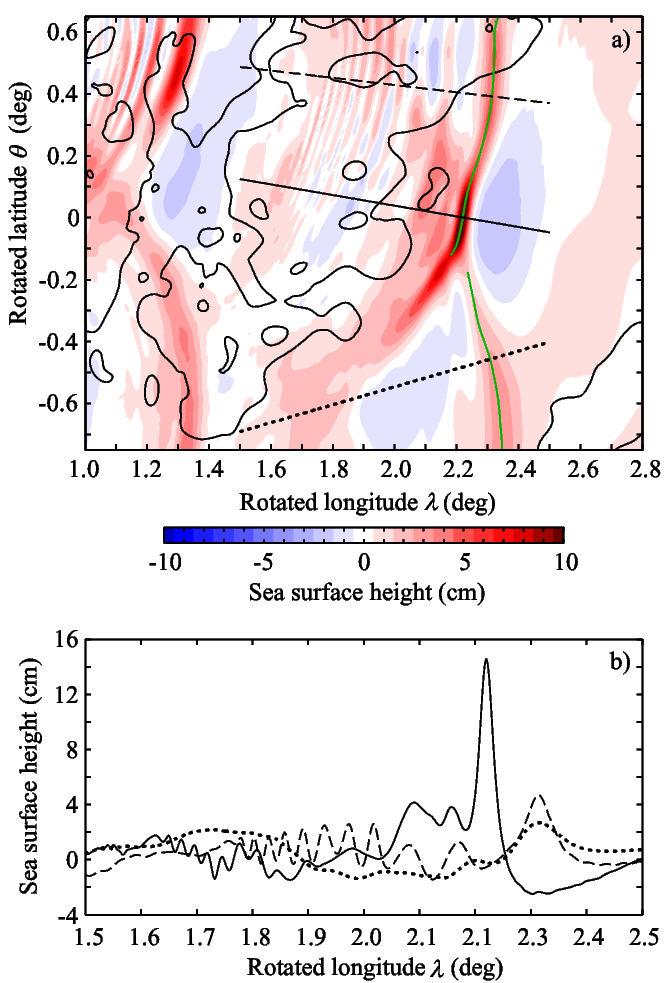
Fig. 5. Sea-surface-height (SSH) expression of modelled oblique ISW interaction under M2 tidal forcing (Full Coriolis case, amplitude unadjusted for topographic variation). (a) SSH in the region shown in Fig. 3b, and (b) profiles of SSH along solid, dashed, and dotted lines shown in panel (a). Green line in (a) shows ISW trough line calculated from vertical velocity. Mean sea level and M2 tide are removed by subtracting mean of modelled SSH time-series at each grid point, and then by least-square fitting of sinusoidal function with M2 tidal frequency to SSH time-series. Figure taken from Shimizu and Nakayama (2017, J. Geophys. Res.-Oceans).
Motivation
In the fields of surface water waves and plasma, it is well-known that the oblique interaction of two solitary waves could enhance the amplitude by a factor of up to 4 (i.e., twice the linear superposition) through the development of a (Mach) stem1),8),12),14),15),17)(Fig. 1). However, this process has seldom been investigated for internal solitary-like waves (ISWs, or internal solitons) in the ocean, despite observations of its surface signature by remote sensing4),11),16),18),19). We investigate oblique ISW interaction in the Andaman Sea with particular focus on the effects of topography and Earth's rotation, because they make the oblique ISW interaction in the ocean different from that in other fields of physics. This study began when my collaborator, Prof. Keisuke Nakayama, identified the occurrence of oblique ISW interaction in early results of my MITgcm ISW modelling, and introduced me to the topic.
Methods
To analyse oblique ISW interaction under realistic oceanic conditions, we use the Miles theory13) but with the following extensions:
- Small-but-finite incident angles, based on studies on surface water waves7),9),20);
- Unequal incident wave amplitudes, based on mathematical studies7); and
- Transitional response, based on studies in plasma physics6).
The theory for the asymptotic state (after sufficiently long interaction) depends on the following parameters: \begin{align} a_s&=\frac{A_s}{\bar{A}}, \\ \kappa&=\frac{\text{tan} \Psi}{\sqrt{2\alpha \bar{A}/c} \text{cos} \Psi}, \\ \sigma&=\frac{1}{2}\sqrt{\frac{\Delta A}{\bar{A}}}, \\ \sqrt{\alpha \bar{A}}&=\left( \sqrt{\alpha A_2}+\sqrt{\alpha A_1} \right)/2, \\ \sqrt{\alpha \Delta A}&= \sqrt{\alpha A_2}-\sqrt{\alpha A_1}, \end{align}
where $A_1$, $A_2$, $A_s$ are respectively the amplitude of the first incident, second incident, and stem-like ISWs, $\alpha$ is the quadratic nonlinear coefficient in the KdV theory, and $\Psi$ is the incident angle. The theory shows that the maximum amplification $a_s=4$ occurs when $\kappa=1$ (Fig. 2).
For our 3-D ISW modelling, we use MITgcm10), realistic topography and stratification, and (spatially-varying) monochromatic M2 tidal forcing. To investigate the effects of Earth’s rotation, we consider the following 3 cases:
- Full Coriolis (including both vertical and horizontal components of Earth’s angular velocity);
- Traditional Coriolis (including only the vertical component)2); and
- No Coriolis.
Results
The model output for Full Coriolis case (Fig. 3) shows that the interaction of ISWs with ~10-m and ~20-m amplitudes ('Incident 1' and 'Incident 2') produced an ISW with >50-m amplitude (labelled as 'Stem-like'), confirming the nonlinear enhancement of ISW amplitudes under realistic topographic and Coriolis effects. After adjusting the amplitudes for significant lateral topographic amplitude variation (by a factor of up to 2) and considering the transitional response, the simulated interaction is found to be approximately consistent with the extended Miles theory (i.e., $a_s \approx 4 $ when $\kappa \approx 1$ after sufficiently long interaction in Fig. 4). Although Earth's rotation has little effect on ISW propagation due to the low latitude (~9°N), Earth's rotation has considerable effects on the oblique interaction.
Implications
- Amplitude variation due to lateral topographic effects does not appear to have been studied, and we had to resort to empirical amplitude adjustment. It needs to be investigated in the future.
- Since the horizontal component of Earth's rotation is unimportant, the effects of Earth's rotation can be studied using rotation-modified Kadomtsev-Petviashvili (KP) equation3),5).
- Oblique ISW interaction is potentially important for mixing, sediment resuspension, and offshore structures and operations, because it could decrease the gradient Richardson number, and increase bottom shear stress and forces on offshore structures, by an order of magnitude.
- Although it appears difficult to estimate the spatial and temporal distribution of stem-like ISW development with the current observational and modelling capabilities, potential observation by the next-generation swath-wide satellite altimeter might begin to shed light on the distribution (Fig. 5).
Related Publications
Details are available in
Data are available in
Acknowledgements
This modelling project was partly funded by Research Connections Grant from Australian Department of Industry, Innovation, and Science, RPS MetOcean Pty Ltd., and CSIRO.
References
- Funakoshi, M. 1980. Reflection of obliquely incident solitary waves. Journal of the Physical Society of Japan, 49: 2371-2379.
- Gerkema, T., J. T. F. Zimmerman, L. R. M. Maas, and H. van Haren. 2008. Geophysical and astrophyisical fluid dynamics beyond the traditional approximation. Reviews of Geophysics, 46: RG2004, doi:10.1029/2006RG000220.
- Grimshaw, R., C. Guo, K. Helfrich, and V. Vlasenko. 2014. Combined effect of rotation and topography on shoaling oceanic internal solitary waves. Journal of Physical Oceanography, 44: 1116-1132, doi:10.1175/JPO-D-13-0194.1.
- Helfrich, K. R., and W. K. Melville. 2006. Long nonlinear internal waves. Annual Review of Fluid Mechanics, 38: 395-425.
- Kadomtsev, B. B., and V. I. Petviashivili. 1970. On the stability of solitary waves in weakly dispersing media. Soviet Physics, Doklady, 15: 539-541.
- Kaup, D. J. 1981. Nonlinear resonances and colliding spherical ion-acoustic solitons. Physica, 2D: 389–394.
- Kodama, Y. 2010. KP solitons in shallow water. Journal of Physics A: Mathematical and Theoretical, 43: 434004, doi:10.1088/1751-8113/43/43/434004.
- Lonngren, K. E. 1983. Soliton experiments in plasmas. Plasma Physics, 25: 943-982.
- Li, W., H. Yeh, and Y. Kodama. 2011. On the Mach reflection of a solitary wave: revisited, Journal of Fluid Mechanics, 672: 326-357, doi:10.1017/S0022112010006014.
- Marshall, J., A. Adcroft, C. Hill, L. Perelman, and C. Heisey. 1997. A finite-volume, incompressible Navier-Stokes model for studies of the ocean on parallel computers. Journal of Geophysical Research - Oceans, 102: 5753–5766.
- Maxworthy, T. 1980. On the formation of nonlinear internal waves from the gravitational collapse of mixed regions in two and three dimensions. Journal of Fluid Mechanics, 96: 47-64.
- Melville, W. K. 1980. On the Mach reflexion of a solitary wave. Journal of Fluid Mechanics, 98: 285-297.
- Miles, J. W. 1977. Resonantly interacting solitary waves. Journal of Fluid Mechanics, 79: 171-179.
- Miles, J. W. 1980. Solitary waves. Annual Review of Fluid Mechanics, 12: 11-43.
- Nakamura, Y. 1982. Experiments on ion-acoustic solitons in plasma. IEEE Transactions on Plasma Science, PS-10: 180-195.
- New, A. L., J. M. Magalhaes, and J. C. B. da Silva. 2013. Internal solitary waves on the Saya de Malha bank of the Mascarene Plateau: SAR observations and interpretation. Deep Sea Research, 179: 50-61, doi:10.1016/j.dsr.2013.05.008.
- Tanaka, M. 1993. Mach reflection of a large-amplitude solitary wave. Journal of Fluid Mechanics, 248: 637-661.
- Wang, C., and R. Pawlowicz. 2012. Oblique wave-wave interactions of nonlinear near-surface internal waves in the Strait of Georgia. Journal of Geophysical Research - Oceans, 117: C06031, doi:10.1029/2012JC008022.
- Xue, J., H. C. Graber, B. Lund, and R. Romeister. 2013. Satellite observation of a zipper-like internal wave-wave interaction pattern in the mid-Atlantic Bight. 2013 IEEE International Geosciences and Remote Sensing Symposium - IGARSS, 1571-1574, doi: 10.1109/IGARSS.2013.6723089.
- Yeh, H., W. Li, and Y. Kodama. 2010. Mach reflection and KP solitons in shallow water. European Physical Journal - Special Topics, 185: 97-111, doi:10.1140/epjst/e2010-01241-0.