Research
Physical uniqueness of higher-order KdV theory for continuously stratified fluids
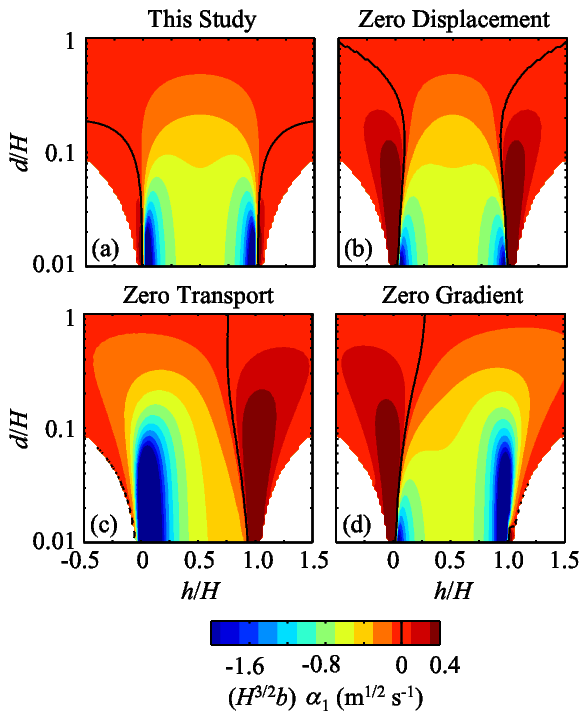
Fig. 1. Comparison of normalized cubic nonlinear coefficient $\alpha_1$ for 1st baroclinic mode under different auxiliary conditions, which has been considered arbitrary. Stratification is hyperbolic tangent $\rho(Z) = \rho_0 + 0.5 \Delta \rho \left( 1- \text{tanh} ((Z+h)/d) \right)$, where $Z$ is the undisturbed height of isopycnals, $\rho_0$ is the reference density, and $\Delta \rho$, $h$, and $d$ are free parameters. (a) Proposed spectral theory, and (b-d) previous theory with different auxiliary condition. Normalization uses water depth $H$ and $b=\sqrt{10^{-3} \rho_0 / \Delta \rho}$.
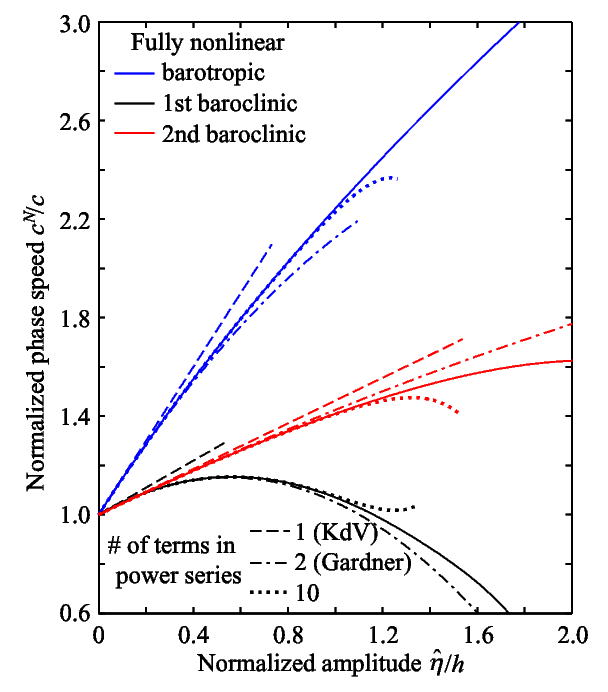
Fig. 2. An example of hydrostatic, fully nonlinear phase speeds $c^N$ for barotropic, 1st baroclinic, and 2nd baroclinic modes under hyperbolic tangent stratification. Solid and broken lines show full and power-series solutions, respectively. Horizontal axis is scaled isopycnal-displacement amplitude of corresponding vertical mode.
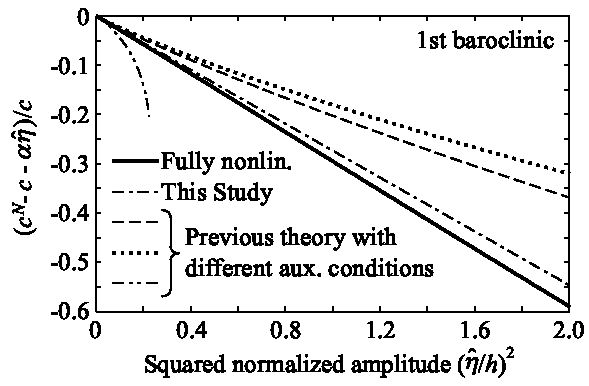
Fig. 3. An example of normalized deviation of nonlinear phase speeds $c^N$ from 1st-order theory under different auxiliary conditions. Results are for 1st baroclinic mode, and stratification is hyperbolic tangent (but different from that used in Fig. 2). Note that slope at $\hat{\eta}=0$ is normalized cubic nonlinear coefficient when amplitude is defined as $\hat{\eta}$, since horizontal axis is squared normalized amplitude.
Motivation
The 2nd-order Korteweg-de Vries (KdV) equation and the Gardner equation are often used to study internal solitary waves with relatively large amplitudes. The Gardner equation is4)
\begin{align} A_t+\left(c+\alpha A + \alpha_1 A^2\right) A_x+\beta A_{xxx} = 0, \end{align}and the associated wave field is
\begin{align} \eta \sim \phi A+T_n A^2, \end{align}where $A$ is some amplitude of isopycnal displacement, $c$ is the linear phase speed for long waves, $\alpha$, $\alpha_1$, and $\beta$ are coefficients, $\eta$ is the (vertically dependent) isopycnal displacement field, $\phi$ is hydrostatic linear vertical mode of interest, and $T_n$ is the nonlinear correction function. Unfortunately, the application of higher-order KdV-type equations to geophysical problems is hindered because higher-order corrections, such as $\alpha_1$ and $T_n$, are considered to be nonunique (or arbitrary) in continuously stratified fluids7) (see Fig. 1 for an example). This study aims to reduce the arbitrariness by proposing that the higher-order KdV theory can be made unique in physical senses.
Methods
The previous higher-order KdV theories3),5),7) are based on the asymptotic approach by Benney1). I use the generalized Fourier (or spectral) approach based on vertical modes, also used by Benney1). This is because there is no need to specify arbitrary auxiliary conditions in the spectral approach, and because it allows the derivation of hydrostatic fully nonlinear gravity wave solutions, which can be used to check the results of the previous asymptotic theories. I also use the isopycnal coordinate, so that the results can be checked against the well-known formulae for two-layer stratification2),6).
Results from Spectral Approach
The derivation of the Gardner equation by the spectral approach yields the following results without arbitrariness:
\begin{align} \alpha =& \frac{3c_p}{2h_p} N_{ppp},\\ \alpha_1=&-\frac{\alpha^2}{6 c_p}+\frac{3}{4} \sum_{q \neq p} { \frac{c_p N_{ppq}^2}{h_p h_q} \frac{5 c_p^2+4 c_q^2}{c_p ^2- c_q^2}},\\ T_n=&\frac{3}{2} \sum_{q \neq p} \frac{N_{ppq}}{h_p} \frac{c_p^2}{c_p^2-c_q^2} \phi_q, \end{align}where the subscripts $p$ and $q$ respectively indicate the mode of interest and the rest of the modes,
\begin{align} \frac{1}{h_n} \equiv \int^0_{-H} {\frac{d \phi_n}{dZ} \frac{d \phi_n}{dZ} dZ} \:\: (n=p,q),\\ N_{ppq} \equiv h_p h_q \int^0_{-H} {\frac{d \phi_p}{dZ} \frac{d \phi_p}{dZ} \frac{d \phi_q}{dZ} dZ}, \end{align}$Z$ is the undisturbed height of isopycnals, and $H$ is the water depth. Note that the amplitude $A$ in the spectral approach is given by the generalized Fourier coefficient under arbitrary nonlinearity
\begin{align} \hat{\eta}_p = c_p^{-2} h_p \left< \phi_p, \eta \right>, \end{align}where the inner product is defined as
\begin{align} \left< a, b \right> \equiv a_s g b_s + \int^0_{-H}{a \frac{d \rho}{dZ} b dZ}, \end{align}and the subscript $s$ indicates the value at the water surface.
Comparisons with Simple Internal Wave Solution
I compared the above results with hydrostatic fully nonlinear solutions, or simple (or Riemann) wave solutions8),10), for continuously stratified fluids (Fig. 2; see also Fully-nonlinear Simple Internal Waves). They extend the solutions for homogeneous8) and two-layer9) fluids to continuously stratified fluids. The power-sereis expansion of the fully nonlinear solution yields the above $\alpha_1$ and $T_n$, confirming that they are unique in the physical sense of Holloway et al.5) (i.e., the solutions need to be unique for "physical" variables, such as phase speed, although "modal" variables, such as modal amplitudes, are nonunique.)
Reason for uniqueness in spectral approach
Why does no arbitrariness appear in the spectral approach? To answer this question, it is convenient to compare the vertically integrated available potential energy of the original (Euler) equations, $P=\rho_0 \left< \eta, \eta \right>/2$, which is positive definite by definition. In the previous and proposed theories, $P$ is respectively given by
\begin{align} P \sim& \frac{\rho_0 }{2} \left< \phi, \phi \right>A^2+ \left< \phi, T_n \right> A^3,\\ P \sim& \frac{\rho_0 }{2} \left< \phi, \phi \right>\hat{\eta}_p^2. \end{align}Note that the available potential energy is positive definite in the lower (proposed) expression, but not so in the upper (previous) expression. The consistency of the two requires
\begin{align} \left< \phi, T_n \right>=0. \end{align}This is implicitly assumed in the spectral approach, and provides a unique auxiliary condition. The argument can be extended to arbitrary nonlinearity because the positive definiteness of $P$ in the spectral approach is guaranteed by Parseval's theorem.
Discussion
This study shows two ways to reduce/remove the nonuniqueness (or arbitrariness) of the higher-order KdV-type theory.
1. Consistent definitions of wave amplitude and nonlinear correction
The simple-wave solutions show that the previous theories also provide correct asymptotic expansion of the fully nonlinear solution (the physical uniqueness of Holloway et al.5)), provided that consistent definitions are used for the wave amplitude and nonlinear correction (e.g., the amplitude $A$ is converted to equivalent $\hat{\eta}_p$ in Fig. 3; note that the slope at $\hat{\eta}_p=0$ is the same under an arbitrary auxiliary condition). The consistent definitions is essential when a KdV-type theory is compared against measurements or outputs from a fully nonlinear numerical model.
2. Positive definiteness of vertically-integrated available potential energy
This provides a unique auxiliary condition. In some applications, it might be desirable to reduce the error in the phase speed by "tuning" against some reference7), with accepting error in $P$. However, such reference is often unavailable in geophysical applications. Furthermore, unlike the amplitude $A$ in the asymptotic theory, the generalized Fourier coefficient $\hat{\eta}_p$ always exists and provides a good prognostic variable even under full nonlinearity (Fig. 2). This auxiliary condition might be useful as a reasonable default choice when reference data for "tuning" is unavailable.
Related Publications
Details are available in
References
- Benney, D. J. 1966. Long non-linear waves in fluid flows. Journal of Mathematical Physics, 45: 52-63.
- Djordjevic, V. D., and L. G. Redekopp. 1978. The fission and disintegration of internal solitary waves moving over two-dimensional topography. Journal of Physical Oceanography, 8: 1016-1024.
- Grimshaw, R., E. Pelinovsky, and O. Poloukhina. 2002. Higher-order Korteweg-de Vries models for internal solitary waves in a stratified shear flow with a free surface. Nonlinear Procesees in Geophysics, 9: 221-235.
- Helfrich, K. R., and W. K. Melville. 2006. Long nonlinear internal waves. Annual Review of Fluid Mechanics, 38: 395–425.
- Holloway, P. E., E. Pelinovsky, and T. Talipova. 1999. A generalized Korteweg-de Vries model of internal tide transformation in the coastal zone. Journal of Geophysical Research - Oceans, 104: 18333-18350.
- Koop, C. G., and G. Butler. 1981. An investigation of internal solitary waves in a two-fluid system. Journal of Fluid Mechanics, 112: 225-251.
- Lamb, K. G., and L. Yan. 1996. The evolution of internal wave undular bores: comparisons of a fully nonlinear numerical model with weakly nonlinear theory. Journal of Physical Oceanography, 26: 2712-2734.
- Lighthill, J. 1978. Waves in fluids. Cambridge University Press.
- Ostrovsky, L. A., and J. Grue. 2003. Evolution equations for strongly nonlinear internal waves. Physics of Fluids, 15: 2934-2948.
- Whitham, G. B. 1974. Linear and nonlinear waves. Wiley.