Research
Linear Modal Analysis with Damping
Energetics and Damping of Basin-Scale Internal Waves in Lake Kinneret
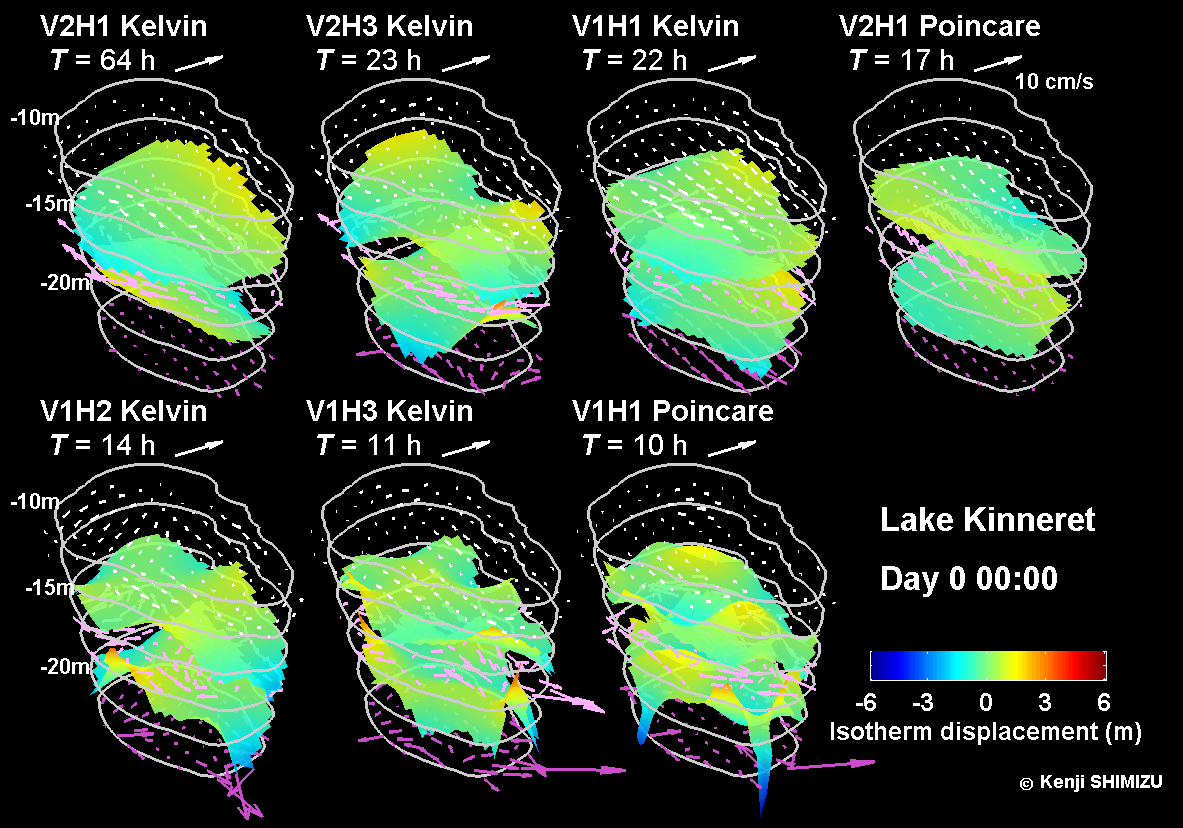
Fig. 1. Internal wave modes in Lake Kinneret computed assuming three-layer stratification. Color shading and arrows show interface displacements and layer-averaged velocities, respectively.
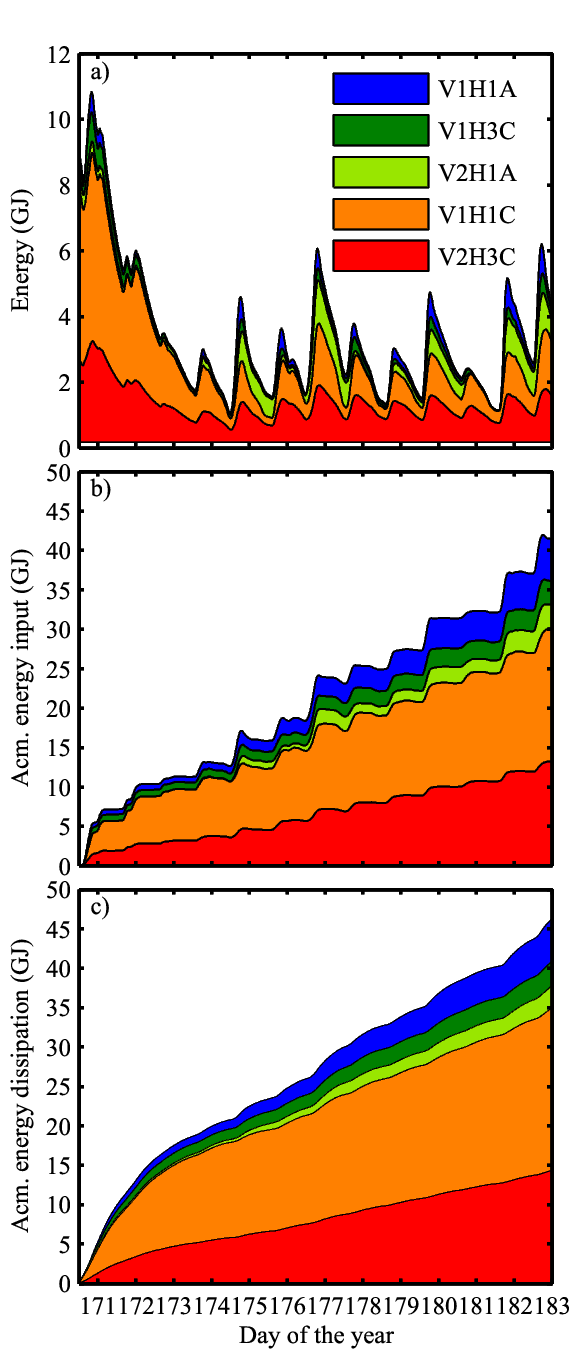
Fig. 2. Estimated energetics of basin-scale internal waves over 2001 field campaign. Partitioning of (a) total energy, (b) accumulated rate of work done by winds, and (c) accumulated rate of energy dissipation. Lines show accumulation for each internal wave so that top lines show the sum for five internal waves. V#H#C/A indicates vertical and horizontal modal indices and direction of rotation (C for cyclonic Kelvin waves, A for anticyclonic Poincaré waves). Reformatted from Shimizu and Imberger (2008, Limnol. Oceanogr.).
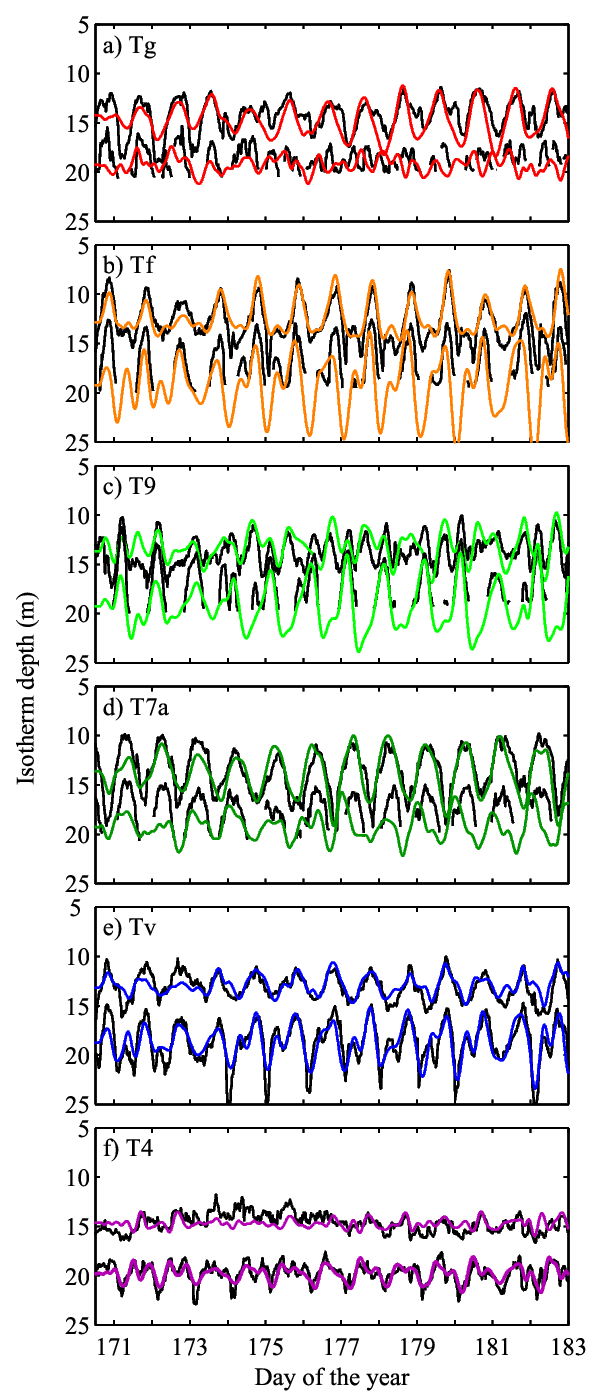
Fig. 3. Comparison of 25°C and 19°C isotherm displacements at six stations distributed throughout Lake Kinneret over 2001 field campaign. Black: observation (detrended), colour: predicted. Reformatted from Shimizu and Imberger (2010, Limnol. Oceanogr.).
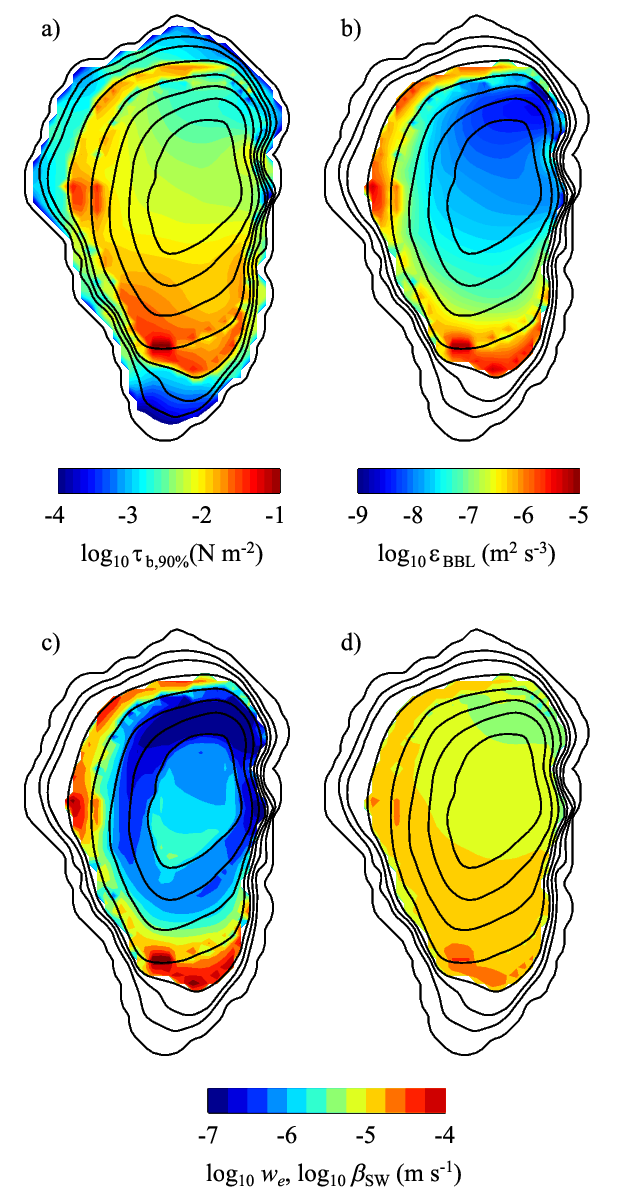
Fig. 4. Spatial distribution of parameters related to near-bottom mass transport. (a) Bottom shear stress, (b) dissipation rate averaged in bottom boundary layer (BBL), (c) entrainment rate at the top of BBL, and (d) mass transfer coefficient at sediment–water interface. Values shown are 90th percentile for panel (a) and average for panels (b–d) over 2001 field campaign. BBL thickness is assumed to be a function of depth8), and Schmidt number of 500 (corresponding to O2) is used to estimate the mass transfer coefficient. Black lines show water depth at 5-m intervals. Reformatted from Shimizu and Imberger (2008, Limnol. Oceanogr.).
Motivation
We previously proposed modal analysis for stratified rotating lakes (see Modal analysis - Lake Biwa), which provides a useful tool to conceptually understand the dynamics of basin-scale motions. We initially assumed no damping, but including damping would expand the range of potential applications of the method. In this study, we aimed to extend the modal analysis to include linear damping, and then applied it to Lake Kinneret to investigate damping mechanism, evolution, and energetics of the basin-scale internal waves, and their contribution to near-bottom mass transport.
Approach
Achieving our aim required much more work than we initially expected. In the end, this study had four components.
- To extend the theory of modal analysis to include linear damping.
- To estimate damping rates of the basin-scale internal waves from field data without assuming damping processes. The resulting damping rates and the structure of the waves allowed us to investigate the damping mechanisms.
- To predict damping rates and evolution of the basin-scale internal waves by including a damping mechanism in the numerical method for basin-scale mode computation.
- To estimate parameters related to near-bottom mass transport due to the basin-scale internal waves.
Study Site and Field Data
Lake Kinneret is located in the Jordan Valley in northern Israel. It is about 20-km long, 10-km wide, and 40-m deep. During summer, the lake is forced by a diurnal Mediterranean westerly sea breeze with the typical wind speed of around 10 m/s2). The vertical mode 1, horizontal mode 1 (V1H1) Kelvin wave with ~1 d period often resonates with the wind1). The near-bottom currents induced by the basin-scale internal waves is known to cause resuspension of the sediment, and to create a well-mixed BBL6),8) with distinct water quality3),9).
We used thermistor chain data collected at 6 stations in summer, 20015), and at 2 stations in spring, 200812).
Theory of Modal Analysis with Weak Linear Damping
Following Platzman (1984), we extended the previous theory of modal analysis and the numerical method of basin-scale mode computation to include weak linear damping. The extended numerical scheme provides not only the spatial structure of basin-scale modes and their angular frequency $\omega^{(n)}$, but also their damping rates $\gamma^{(n)}$, where the superscript $n$ is the modal index. The evolutionary equation of modal amplitudes, $a^{(n)}$, is still decoupled for individual modes, and is given by
\begin{align} \frac{d a^{(n)}}{dt} = i \omega^{(n)} a^{(n)} - \gamma^{(n)} a^{(n)} + \frac{f^{(n)}}{e^{(n)}}, \end{align}where $f^{(n)}$ represents forcing due to wind stress, and $e^{(n)}$ is an arbitrary normalization factor of $n$th mode. The corresponding energy equation is
\begin{align} \frac{d E^{(n)}}{dt} = \dot{W}^{(n)} - \dot{D}^{(n)}, \end{align}where $E^{(n)}=\tfrac{1}{2}e^{(n)}|a^{(n)}|^2$ is the total (i.e., available potential plus kinetic) energy, $\dot{W}^{(n)}= a^{(n)*} f^{(n)}$ is the rate of work done by winds, and $\dot{D}^{(n)}=2 \gamma^{(n)} E^{(n)}$ is the rate of energy dissipation.
Fig. 1 shows the structure of the major basin-scale internal waves in Lake Kinneret in summer, calculated assuming three-layer stratification.
Results - Damping Mechanism
To investigate damping mechanisms of the basin-scale internal waves, we initially calculated internal wave modes without damping, but used the modal amplitude equation to look for damping rates that yield best fit of isotherm displacements to the thermistor chain data. The resulting energetics is shown in Fig. 2. We found that the rate of total energy dissipation can be explained by bottom friction with a drag coefficient of $C_b=2.9 \times 10^{-3}$, which is within the typical range in lakes. Therefore, the dominant damping mechanism of the basin-scale internal waves in Lake Kinneret is bottom friction.
Results - Predicting Evolution
Developing a numerical method of basin-scale mode calculation with bottom friction required separate studies on the damping mechanisms of internal waves by boundary friction and simple models of capped bottom boundary layers (BBLs). The use of unsteady Ekman pumping velocity and a layer-averaged BBL model enabled prediction of the damping rates of basin-scale internal waves, and as a result their evolution under periodic wind forcing. The modal analysis successfully predicted the observed isotherm displacements in spring and summer in Lake Kinneret (see Fig. 3 for summer, and Shimizu and Imberger (2010) for spring).
Implications for Near-Bottom Mass Transport
The currents and dissipation rates predicted by modal analysis can be used to investigate the spatial and temporal variability of parameters related to near-bottom mass transport, such as bottom shear stress (for sediment resuspension), entrainment rate at the top of the BBL4), and mass transfer coefficient at the sediment-water interface7). We found that the basin-scale internal waves induce large spatial variability of these parameters in Lake Kinneret (Fig. 4).
Related Publications
Details are available in
Acknowledgements
Substantial part of this study was conducted when I was a PhD candidate at Centre for Water Research, University of Western Australia, with the financial support of Japanese government (MEXT) scholarship and Tokyo-Tech Long-term Overseas Study Support Program. The the field experiment carried out in 2008 was supported under Australian Research Council’s Discovery Projects funding scheme (project DP0773823).
References
- Antenucci, J. P., and J. Imberger. 2003. The seasonal evolution of wind/internal wave resonance in Lake Kinneret. Limnology and Oceanography, 48: 2055–2061.
- Avissar, R., and H. Pan. 2000. Simulations of the summer hydrometeorological processes of Lake Kinneret. Journal of Hydrometeorology, 1: 95–109.
- Eckert, W., J. Imberger, and A. Saggio. 2002. Biogeochemical response to physical forcing in the water column of a warm monomictic lake. Biogeochemistry, 61: 291–307.
- Gloor, M., A. Wüest, and D. M. Imboden. 2000. Dynamics of mixed bottom boundary layers and its implications for diapycnal transport in a stratified, natural water basin. Journal of Geophysical Research - Oceans, 105: 8629–8646.
- Gómez-Giraldo, A., J. Imberger, and J. P. Antenucci. 2006. Spatial structure of the dominant basin-scale internal waves in Lake Kinneret. Limnology and Oceanography, 51: 229–246.
- Lemckert, C., J. Antenucci, A. Saggio, and J. Imberger. 2004. Physical properties of turbulent benthic boundary layers generated by internal waves. Journal of Hydraulic Engineering, ASCE, 130: 58–69.
- Lorke, A., B. Müller, M. Maerki, and A. Wüest. 2003. Breathing sediments: The control of diffusive transport across the sediment-water interface by periodic boundary-layer turbulence. Limnology and Oceanography, 48: 2077–2085.
- Marti, C. L., and J. Imberger. 2006. Dynamics of the benthic boundary layer in a strongly forced stratified lake. Hydrobiologia, 568: 217–233.
- Nishri, A., J. Imberger, W. Eckert, I. Ostrovsky, AND Y. Geifman. 2000. The physical regime and the respective biogeochemical processes in the lower water mass of Lake Kinneret. Limnology and Oceanography, 45: 972–981.
- Platzman, G. W. 1984. Normal modes of the world ocean. Part III: A procedure for tidal synthesis. Journal of Physical Oceanography, 14: 1521–1531.
- Shimizu, K., and J. Imberger. 2008. Energetics and damping of internal waves in a strongly stratified lake. Limnology and Oceanography, 53: 1574-1588.
- Shimizu, K., and J. Imberger. 2010. Seasonal differences in the evolution of damped internal waves in a stratified lake. Limnology and Oceanography, 57: 1449-1462.