Research
Highlights
+ Statistical Model of Nonharmonic Internal Tides
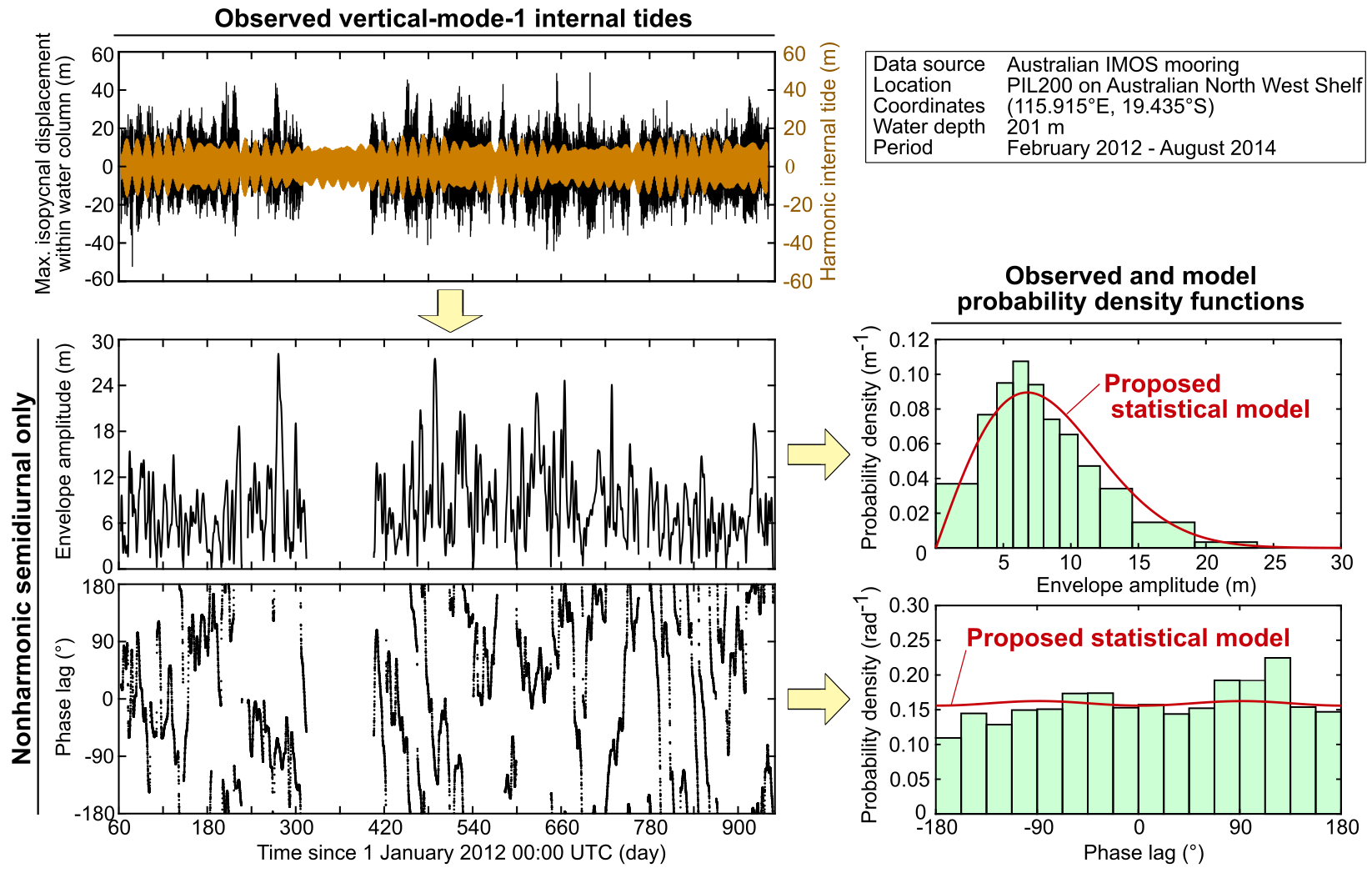
Internal tides are internal waves at tidal frequencies. Although they appear to oscillate like the usual tides, they are known to contain substantial random components because oceanic variability modulates their amplitudes and phases. I developed the first detailed statistical model for the random component of internal tides. The model probability density functions (PDFs) agree with those from observations on Australian North West Shelf. The statistical information is useful for many purposes, as seen in the example of surface waves for engineering applications.
See Statistical Model of Nonharmonic Internal Tides for the details.
+ Combined Adjoint, Statistical, and Stochastic Modelling of Nonharmonic Internal Tides
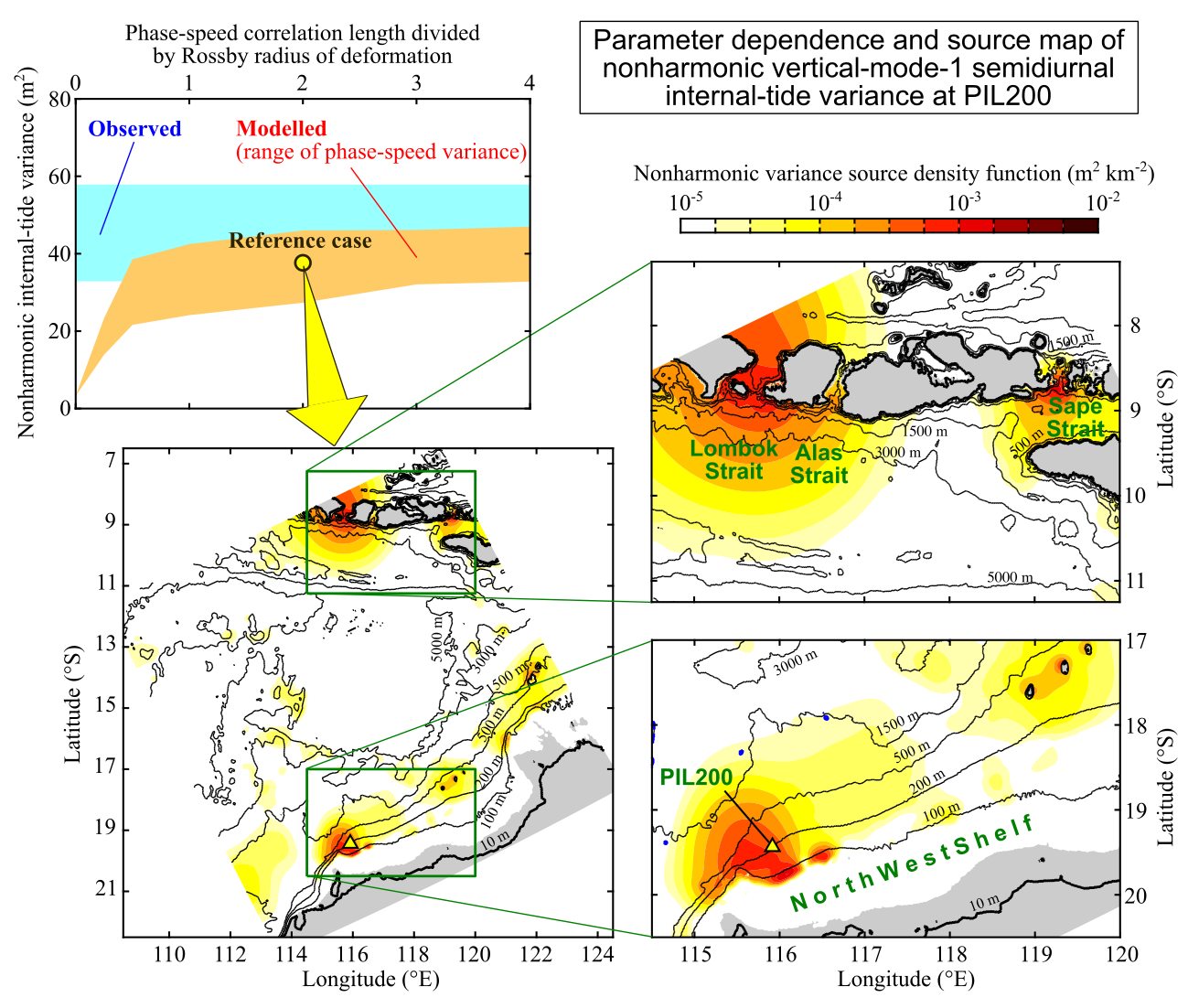
Internal tides are internal waves at tidal frequencies. Although they appear to oscillate like the usual tides, they are known to contain substantial random components because oceanic variability modulates their amplitudes and phases. I developed a completely new process-based model suite for modelling the variance of random internal tides, and for mapping their sources. The results with realistic range of model parameters agree with the observed variance, and revealed new essential parameters for the modulation process. The source maps are useful for planning field measurements and data assimilation in the future.
See Combined Adjoint, Statistical, and Stochastic Modelling of Nonharmonic Internal Tides for the details.
+ Properties of Adjoint Sensitivity under Internal Waves

Fig.3. Adjoint sensitivity of simple-wave amplitude (Riemann variable) $R$ at x ~ 33 km to temperature under semi-diurnal internal waves. (a) "Initial" condition, (b) 5 hrs earlier, and (c) 10 hrs earlier. Black lines show 22 to 30°C isotherms from the forward model at 2°C intervals. Click image to see the movie (1.0MB, not for small screen).
Adjoint sensitivity modeling is a common technique used to solve inverse problems, including so-called four-dimensional variational (4D-Var) data assimilation used in weather forecasts and ocean reanalysis. However, it remains unclear whether physically-sensible and stable adjoint sensitivity modeling is feasible in the presence of internal waves. To my knowledge, this is the first study to demonstrate the feasibility using careful theoretical and numerical analyses. However, the results also imply that the standard form of the objective function, which has been used in data assimilation studies for quasi-geostrophic flows and barotropic tides, could be problematic for internal tides. This study suggests an alternative definition of the objective function.
See Properties of Adjoint Model and Adjoint Sensitivity under Fully-Nonlinear Internal Waves for the details.
+ Fully-Nonlinear Simple Internal Waves
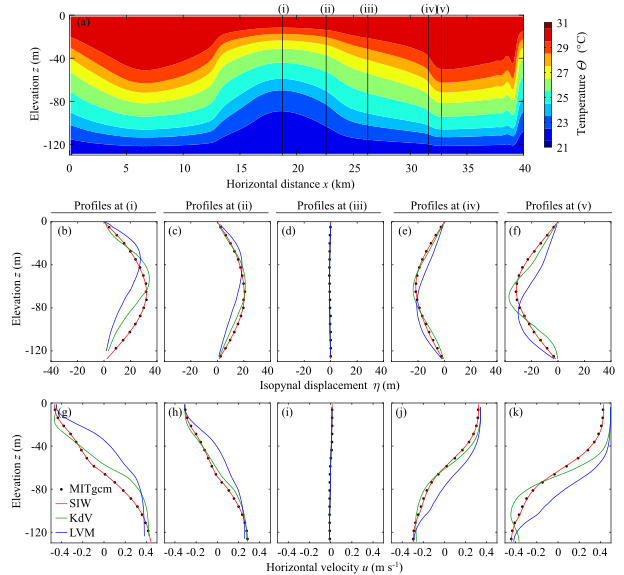
Fig.4. Comparisons of MITgcm outputs and (semi-) analytic solutions. (a) Temperature cross-section from MITgcm, and comparisons of (b-f) isopycnal-displacement and (g-k) horizontal-velocity profiles at locations indicated by vertical lines in panel (a). Abbreviations are SIW: simple-internal-wave theory, KdV: 2nd-order KdV theory, and LVM: linear vertical-mode theory.
The theory of fully-nonlinear, one-directional, non-dispersive waves, called simple waves, provides an important basis to understand fully-nonlinear waves in various fields of physics and engineering. However, simple-wave solution was not available for internal waves in continuously stratified fluids. I have derived semi-analytic fully-nonlinear simple-wave solution for internal waves under continuous stratification, and extended it to include 2nd-order (moderately strong) topographic effects. The figure shows the comparisons with MITgcm simulation and linear and 2nd-order Korteweg-de Vries theories. Note the agreement between red lines (theory) and black dots (MITgcm simulations).
See Fully-nonlinear Simple Internal Waves for the details.
+ 3D Internal Solitary Wave Modelling

Fig. 5. A snapshot of MITgcm ISW modelling output on Australian North West Shelf (around 116.4°E, 19.5°N). From the top, left panels show time-series of surface elevation, time-series of temperature profiles at RPS mooring, and a snapshot of a temperature cross-section along B-B’ line in right panel. Right panel shows a snapshot of temperature at 60 m below mean sea level. Abbreviations are NRA: North Rankin platform by Woodside Energy Ltd., and PIL100: Pilbara 100-m mooring by Australian Integrated Marine Observing System (IMOS). Note the different temperature scales for left and right panels. Image shown by courtesy of RPS MetOcean. © 2016 RPS MetOcean Pty Ltd. Click image to see the movie (1.5MB, not for small screen).
I have been conducting 3D internal solitary wave (ISW) modelling for research and engineering purposes using MITgcm. The movie shows my earliest example of 3D ISW modelling. See Modelling Internal Solitary-like Waves on Australian North West Shelf for the details.
Another example from Andaman Sea is available in Oblique Interaction of Internal Solitary-like Waves in the Andaman Sea.