Research
Linear Modal Analysis
Horizontal Structure and Excitation of Basin-Scale Motions in Lake Biwa

Fig. 1. Internal wave modes in Lake Biwa computed assuming two-layer stratification. Color and arrows show interface displacement and average velocity in upper layer, respectively.
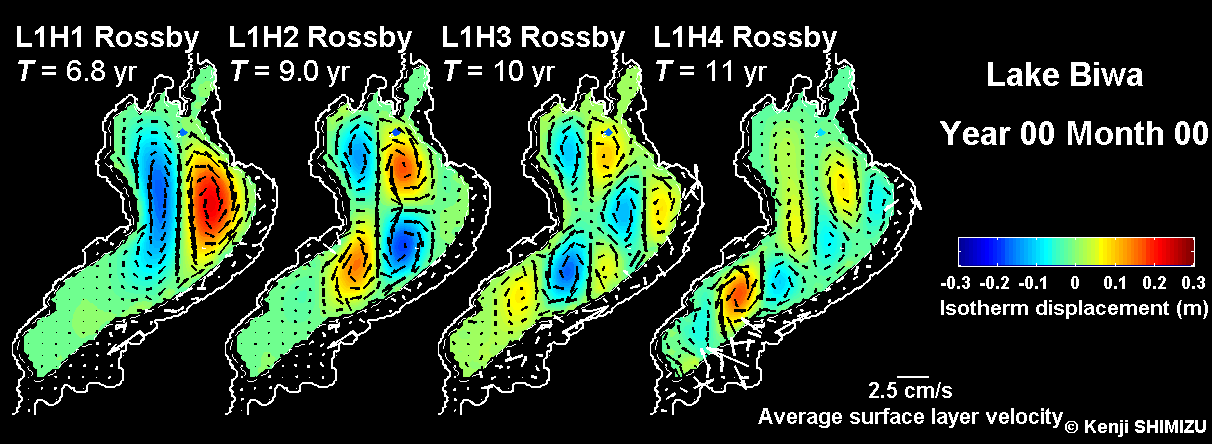
Fig. 2. Rossby wave modes in Lake Biwa computed assuming two-layer stratification. Color and arrows show interface displacement and average velocity in upper layer, respectively. Although phases of these waves keep moving to east, they are standing waves from an energetics point of view.
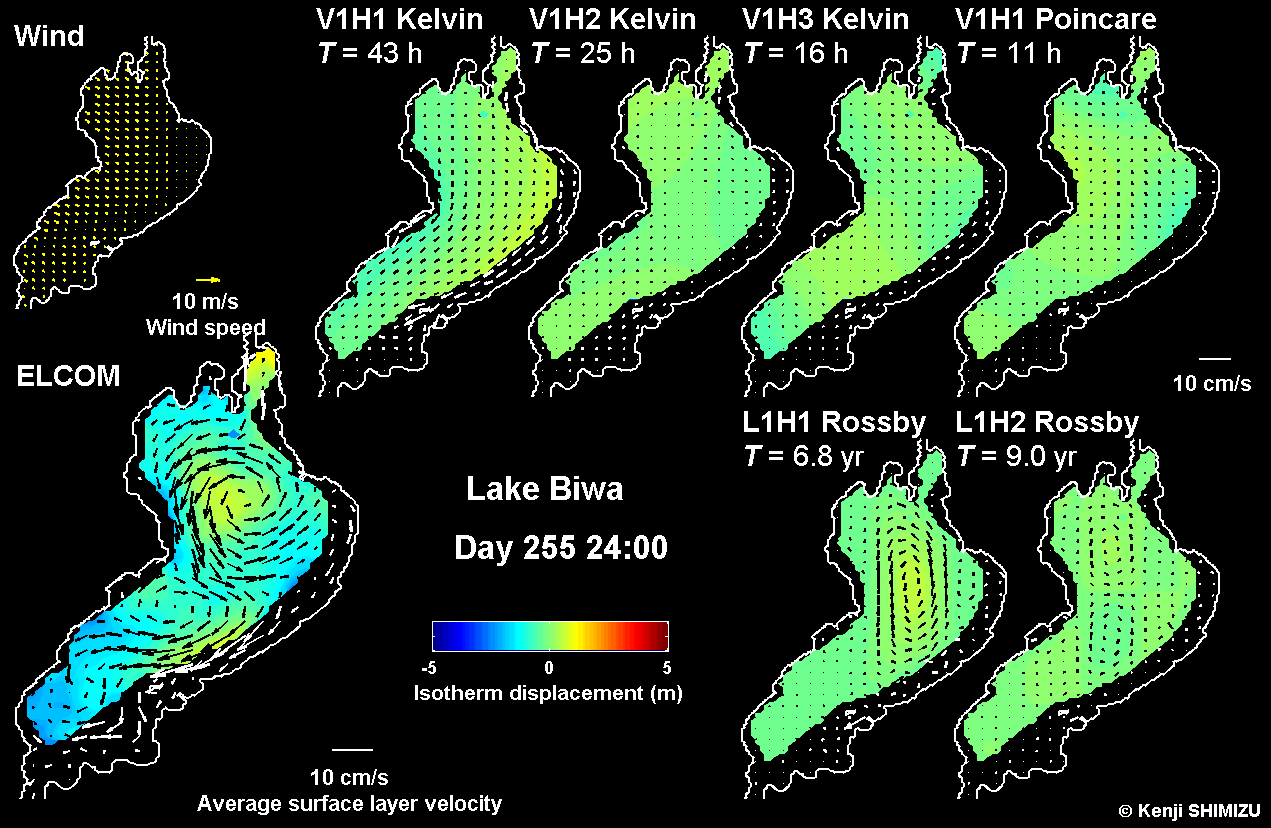
Fig. 3. Results of a CWR-ELCOM simulation with extracted 4 internal wave modes and 2 Rossby wave modes. Color and arrows show interface displacement and average velocity in upper layer, respectively.
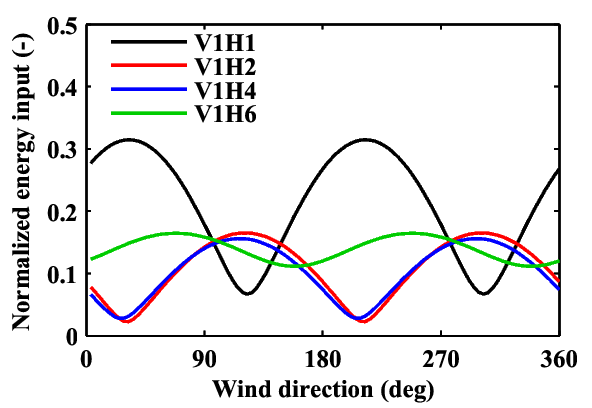
Fig. 4. Effect of wind direction on excitation of different internal wave modes. Vertical axis is normalized maximum energy input from spatially uniform winds. Wind direction is positive clockwise, and 0 when the wind is blowing from the north. V#H#: vertical and horizontal mode number. Reformatted from Shimizu et al. (2007, Limnol. Oceanogr.).
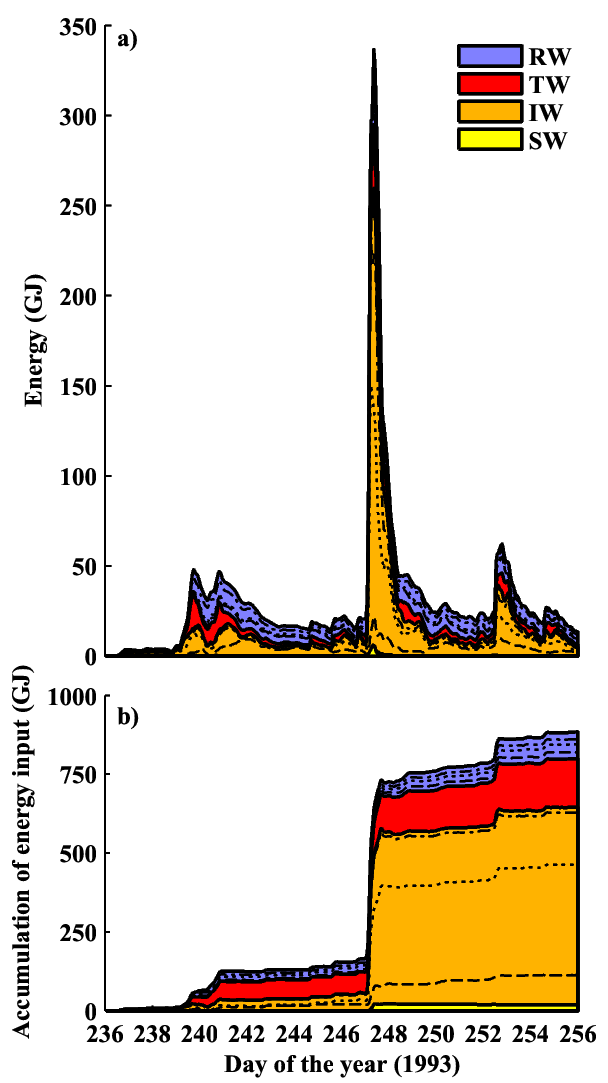
Fig. 5. Energy partitioning among different classes of modes, extracted from the results of a CWR-ELCOM simulation using two-layer approximation. (a) Total energy and (b) accumulated energy input from winds. Solid lines show accumulation for each class, and dashed, dotted, and dash-dot lines correspond to accumulation up to the 1st, 5th, and 10th internal wave modes, but up to 1st, 20th, and 50th Rossby wave modes. RW: Rossby wave, TW: topographic wave, SW: surface wave, and IW: internal wave. Reformatted from Shimizu et al. (2007, Limnol. Oceanogr.).
Motivation
Modal analysis is a common method used to analyse vibration problems in physics and engineering. For two-layer-stratified lakes, the method of calculating basin-scale modes has been known for many years1),7). However, a lack of theoretical understanding prevented physical limnologists from taking full advantage of the method. My idea was to enable a wide range of applications of this method as in other fields, by developing the theory of modal analysis for stratified rotating lakes. We made a first step in theoretical development, and then applied it to Lake Biwa to investigate horizontal structure and excitation of the basin-scale motions.
Study Site
Lake Biwa is the largest lake in Japan, with ~60-km length, ~20-km width, and ~100-m maximum depth. During the stratified period, Lake Biwa supports many basin-scale internal wave modes, as well as strong and persistent gyres (typical current speed ~0.1 m/s).
Basin-Scale Modes
Basin-scale modes in Lake Biwa were computed using two-layer approximation. The internal wave modes are shown in Fig. 1, and the Rossby wave modes in Fig. 2. (The Rossby wave modes have very long periods, and effectively represent quasi-geostropic flows, such as gyres.)
Theory and Applications of Modal Analysis
Following previous theories for homogeneous rotating basins9)-12), basin-scale modes can be used as basis functions for generalized Fourier series. For example, averaged velocity in $k$th layer $\vec{v}_k (\vec{x}, t)$ ($k=1$ and $2$ for upper and lower layer) can be decomposed into modal components as
\begin{align} \vec{v}_k=\sum_n{\vec{v}_k^{(n)} a^{(n)}}, \end{align}where $\vec{v}_k^{(n)}(\vec{x})$ is the complex-valued layer-average velocity due to $n$th mode, and $a^{(n)}(t)$ is its amplitude. Then, neglecting nonlinearity and damping, $a^{(n)}$ follows an decoupled modal amplitude equation:
\begin{align} \frac{d a^{(n)}}{dt} =& i \omega^{(n)} a^{(n)} + \frac{f^{(n)}}{e^{(n)}}, \\ f^{(n)}=&\int{}\vec{v}_1^{(n)*} \cdot \vec{\tau} dS, \end{align}where $\vec{\tau}$ is the wind stress vector, $e^{(n)}$ is an arbitrary normalization factor of $n$th mode, and the integral is taken over the lake surface.
Based on this theory, we proposed the following new applications of modal analysis:
- To understand the effectiveness of wind forcing in exciting different modes using the modal force $f^{(n)}$.
- To extract the amplitudes and energetics of individual modes from the results of numerical simulations based on the modal decomposition (Fig. 3).
Results and Implications for Lake Biwa
- The structure and periods of the computed internal waves agree well with previous observations in Lake Biwa2)-6),8),13).
- The internal wave modes can be preferentially excited by winds depending on wind direction (Fig. 4).
- Excitation of the gyres (Rossby wave modes) requires by wind stress curl.
- The internal waves are effectively excited by winds but dampened within few days, whereas gyres are excited ineffectively but dampened slowly (Fig. 5). This implies the importance of internal waves as energy sources for mixing, and gyres for long-term horizontal transport.
Related Publications
Details are available in
The modal analysis has also been applied to Lake Biwa in winter:
Acknowledgements
This study was conducted when I was a PhD candidate at Centre for Water Research, University of Western Australia, with financial support of Japanese government (MEXT) scholarship and Tokyo-Tech Long-term Overseas Study Support Program.
References
- Bäuerle, E. 1985. Internal free oscillations in the Lake of Geneva. Annals of Geophysics 3: 199–206.
- Endoh, S. 1986. Diagnostic study on the vertical circulation and the maintenance mechanism of the cyclonic gyre in Lake Biwa. Journal of Geophysiscal Research 91: 869-876.
- Endoh, S., and Y. Okumura. 1993. Gyre system in Lake Biwa derived from recent current measurements. Japanese Journal of Limnology 54: 191-197.
- Endoh, S., Y. Okumura, and I. Okamoto. 1995. Field Observation in the North Basin, p. 15-29. In S. Okuda, J. Imberger and M. Kumagai [eds.], Physical Processes in a large lake: Lake Biwa, Japan. American Geophysical Union.
- Kanari, S. 1975. The long-period internal waves in Lake Biwa. Limnology and Oceanography 20: 544-553.
- Kumagai M., Y. Asada, and S. Nakano. 1998. Gyres measured by ADCP in Lake Biwa, p. 199-208. In J. Imberger [ed.], Physical Processes in Lakes and Oceans. American Geophysical Union.
- Lemmin, U., C. H. Mortimer, and E. Bäuerle. 2005. Internal seiche dynamics in Lake Geneva. Limnology and Oceanography 50: 207–216.
- Okamoto, I., and S. Endoh. 1995. Water mass exchange between the main basin and Shiozu Bay, p. 31-42. In S. Okuda, J. Imberger and M. Kumagai [eds.], Physical Processes in a large lake: Lake Biwa, Japan. American Geophysical Union.
- Platzman, G. W. 1972. Two-dimensional free oscillations in natural basins. Journal of Physical Oceanography 2: 117–138.
- Platzman, G. W. 1975. Normal modes of the Atlantic and Indian Oceans. Journal of Physical Oceanography 5: 201–221.
- Platzman, G. W. 1984. Normal modes of the world ocean. Part III: A procedure for tidal synthesis. Journal of Physical Oceanography 14: 1521–1531.
- Proudman, J. 1928. On a general expansion in the theory of the tides. Proceedings of the London Mathematical Society 29: 527–536.
- Saggio, A., and J. Imberger. 1998. Internal wave weather in a stratified lake. Limnology and Oceanography 43: 1780-1795.
- Shimizu, K., J. Imberger, and M. Kumagai. 2007. Horizontal structure and excitation of primary motions in a strongly stratified lake. Limnology and Oceanography 52:2641-2655.