Research
Fully-nonlinear Modal Analysis
Nonlinear Evolution of Internal Kelvin Waves in Lake Constance
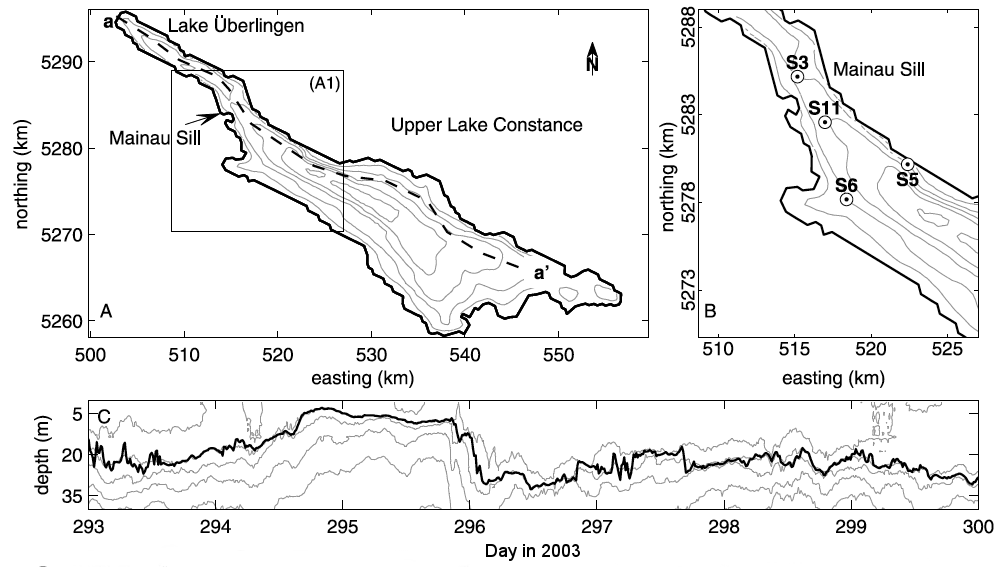
Fig. 1. Field observations in Lake Constance in 2003. (A) Bathymetry of the whole lake, (B) zoom-up of A1 and measurement locations, and (C) thermistor-chain observations at S5. Contours in (A) show isobaths at 50 m intervals, and those in (C) show 6-11 ℃ isotherms. Black line in (C) shows interface depths, calculated as the depths of maximum buoyancy frequency. Reformatted from de la Fuente et al. (2010, J. Geophys. Res. - Oceans)
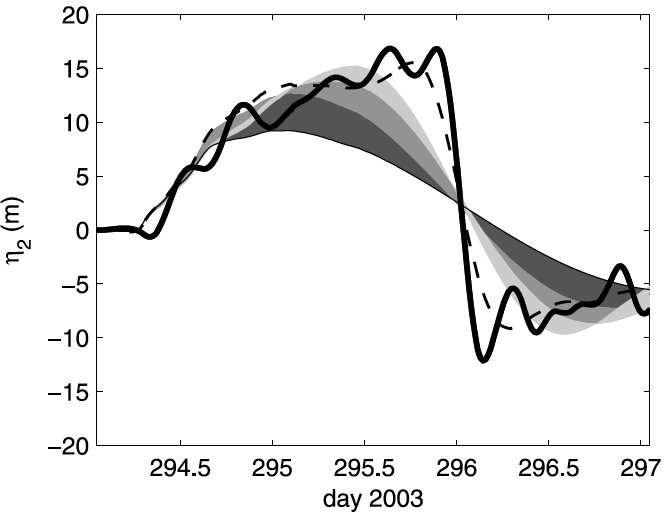
Fig. 2. Evolution of interface displacement at S5 calculated by nonlinear modal analysis. Thin line shows the contribution of fundamental-mode Kelvin wave. Shaded areas, dashed line, and thick solid line show the contributions of the first 3 higher azimuthal modes, the first 10 modes, and all the modes used, respectively. Figure taken from de la Fuente et al. (2010, J. Geophys. Res. - Oceans)
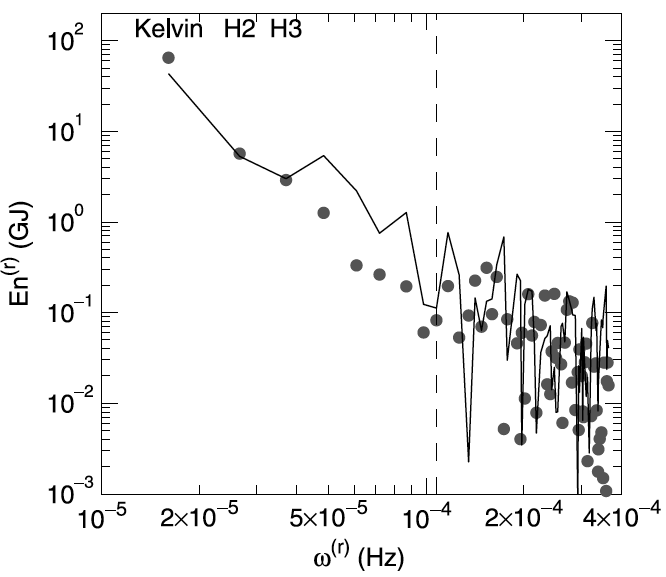
Fig. 3. Pseudo-energy contained in basin-scale internal gravity-wave modes as a function of their natural frequency. Dots and line show "spectra" at Days 295 and 296.4 (before and after Kelvin wave steepening), respectively. Vertical dashed line indicates the inertial frequency. Figure taken from de la Fuente et al. (2010, J. Geophys. Res. - Oceans)
Motivation
Linear modal analysis for a stratified rotating lake was proven to be a useful tool to understand basin-scale internal waves in medium-sized lakes (see examples from Lake Biwa and Lake Kinneret). Since basin-scale internal waves in lakes can steepen and degenerate into solitary waves, it is natural to extend the method to include nonlinearity. I developed the nonlinear theory during my PhD3), but it was my collaborator, Alberto de la Fuente (Uni. of Chile, Santiago), who applied the theory to Lake Constance.
Theory of Fully-nonlinear Modal Analysis
I had to come up with a mathematical trick to extend the theory of the modal analysis to include full nonlinearity. This is because it is much preferred to have the kinetic energy in a quadratic form from a mathematical view point, but nonlinearity introduces cubic terms. One solution was to expand the layer-averaged velocity $\vec{v}_k$ and the layer transport $\vec{q}_k=h_k \vec{v}_k$ ($h_k$ is the layer thickness and $k$ is a layer index) into modal components individually, following the idea by Imai2) who proposed a similar approach to define energy in electromagnetism. Omitting further details, the amplitude of individual modes $a^{(n)}$ follow evolutionary equations that look like, neglecting forcing and damping terms, \begin{align} \frac{d a^{(n)}}{dt} = i \omega^{(n)} a^{(n)} + \sum_{l,m} n^{(n,l,m)} a^{(l)} a^{(m)}, \end{align} where $\omega^{(n)}$ is the angular frequency of $n$th mode, and $n^{(n,l,m)}$ is the nonlinear interaction coefficient among $n$th, $l$th, and $m$th modes. There is also equations corresponding to the modal energy equations \begin{align} \frac{d E^{(n)}}{dt} = \sum_{l,m} \dot{F}^{(n,m)}, \end{align} where $\dot{F}^{(n,m)}$ is the nonlinear "energy" transfer rate. Although the sum of $E^{(n)}$ over all the modes is equal to the total energy, $E^{(n)}$ is not a positive definite quantity under strong nonlinearity. So $E^{(n)}$ should be regarded as a pseudo-energy.
Study Site and Observations
Lake Constance is a long, deep lake located between Germany and Switzerland (Fig. 1A,B). It consists of the main basin (Upper Lake Constance) and a sub-basin (Lake Überlingen) separated by Mainau Sill. Previous studies showed that the fundamental mode Kelvin wave with ~90 h period transforms into an internal surge as it travels along the northern shore1), and then degenerates into solitary and other high-frequency internal waves4).
Fig. 1C shows an example of the steepened basin-scale internal Kelvin wave in the lake, observed near the northern shore by a thermistor chain in 2003.
Model Set-up
Assuming two-layer stratification, we calculated 360 basin-scale modes with periods between 5.4 and 105 d. The modes include Kelvin and Poincaré (gravity) waves, and topographic waves.
The nonlinear model is run for 3 days from Day 294 in 2003. To excite lower-mode internal Kelvin waves, the model is forced with a measured northwesterly wind event with ~10 m/s wind speed and ~12 h duration. Then the model is left free for 2.5 days to investigate the nonlinear evolution of the Kelvin waves.
Results and Discussion
The model reproduced the steepened Kelvin wave at S5 with reasonable amplitude and shape (Fig. 2). In modal analysis, the steepening is represented by superposition of higher azimuthal-mode Kelvin waves that are excited by nonlinear interaction among different modes. The nonlinear transfer towards higher modes (or cascade) can also be seen in the "energy spectra" before and after the wave steepening (Fig. 3).
The above results are familiar from the spectral approach in fluid mechanics, for example, that used in the turbulence theory and Direct Numerical Simulation (DNS). This is not surprising because the two becomes equivalent if we simplify the Kelvin waves in Lake Constance as internal seiche in a non-rotating rectangular basin. The theory proposed in this study extends the nonlinear spectral method to a stratified rotating basin with realistic bathymetry.
Related Publications
Details are available in
Acknowledgements
This study was supported by the project Mecesup UCH0310, the office facilities at Laboratoire Magma et Volcans of Universite Blaise Pascal of Clermont-Ferrand, the University of Western Australia, and the Western Australian Water Corporation.
References
- Appt, J., J. Imberger, and H. Kobus. 2004. Basin‐scale motion in stratified Upper Lake Constance. Limnology and Oceanography, 49: 919–933.
- Imai, I. 1991. On the definition of macroscopic electromagnetic quantities. Journal of the Physical Society of Japan, 60: 41000-4118.
- Shimizu, K. 2008. Application of modal analysis to strongly stratified lakes. Ph.D. Thesis, University of Western Australia, Crawley, Western Australia, Australia.
- Vlasenko, V. I., and K. Hutter 2002. Transformation and disintegration of strongly nonlinear internal waves by topography in stratified lakes. Annales of Geophysics, 20: 2087–2103.