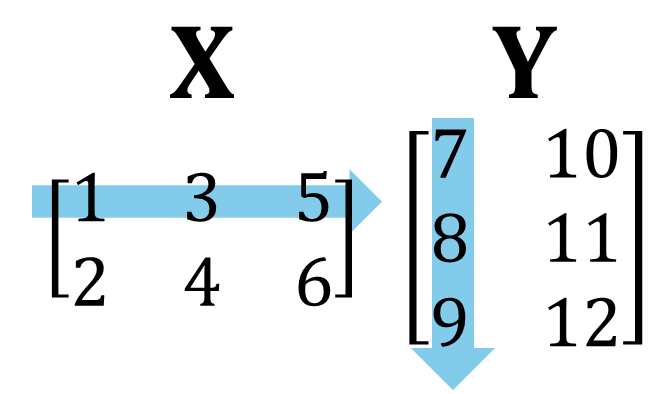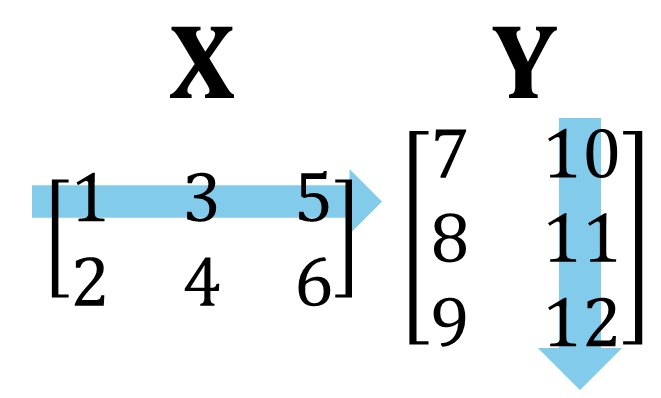本講義資料では，因子分析および構造方程式モデリングの数理的な性質を線形代数によって説明しています。 そのため， チャプター 5 で回帰分析を線形代数的に表現するところから始まり，ベクトルや行列の演算がところどころに登場します。
そこで本補足チャプターでは，線形代数の表記の意味や基本的な演算など，この講義資料を理解するうえで必要な最低限の知識を確認していきます。
B.1 ベクトルと行列
線形代数では，「ベクトル」や「行列」を使っていろいろな計算を行います。 高校数学では（世代によっても異なるのですが）ベクトルを「座標空間上の矢印の足し算・引き算」という感じで学んでいた人が多いかもしれません。 確かに線形代数はそのように幾何学的に利用されるものではあるのですが，本講義の資料を理解するにあたっては，とりあえずベクトルや行列は単に複数のデータ・変数を簡潔にまとめて表すためのツールくらいに思っておいてもOKです。
B.1.1 ベクトル
ベクトル (vector) は，複数の数字が縦または横に並んだものです。 一般的にはアルファベット小文字のボールド体で表され，例えば\(K\)個の数字が縦あるいは横に並んだ \[ \mathbf{x} = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_K \end{bmatrix} \qquad \mathbf{y} = \begin{bmatrix} y_1 & y_2 & \cdots & y_K \end{bmatrix} \tag{B.1}\] はそれぞれ\(K\)次元（縦）ベクトル，\(K\)次元横ベクトルと呼ばれたりします1。 このあとの様々な演算では，ベクトル（および）行列の大きさがとても重要になるので，できる限り常にベクトルのサイズは意識して把握しておいてください。
B.1.2 行列
行列 (matrix) は，複数の数字が縦横に並んだものです。 一般的にはアルファベット大文字のボールド体で表され，例えば以下の行列 \[ \mathbf{X} = \begin{bmatrix} x_{11} & x_{12} &\cdots & x_{1K} \\ x_{21} & x_{22} &\cdots & x_{2K} \\ \vdots & \vdots &\ddots & \vdots \\ x_{P1} & x_{P2} &\cdots & x_{PK} \end{bmatrix} \tag{B.2}\] は，\(P\times K\)行列などと呼ばれます。 ベクトルのときと同様に，行列のサイズはとても重要です。 また，行列\(\mathbf{X}\)の中で上から\(p\)番目，左から\(k\)番目（すなわち\(p\)行目・\(k\)列目）の要素のことを(p,k)要素と呼んだりもします。
行列は，ベクトルを拡張したものという位置づけでもあります。 すなわち(B.2)式の行列は，\(K\)個の（\(P\)次元）縦ベクトルが横に並んだ形 \[ \mathbf{X} = \begin{bmatrix} \mathbf{x}_1 & \mathbf{x}_2 & \cdots & \mathbf{x}_K \end{bmatrix}, \quad \text{ただし} \mathbf{x}_k = \begin{bmatrix} x_{1k} \\ x_{2k} \\ \vdots \\ x_{Pk} \end{bmatrix} \tag{B.3}\] あるいは\(P\)個の（\(K\)次元）横ベクトルが縦に積み重なった形 \[ \mathbf{X} = \begin{bmatrix} \mathbf{x}_1 \\ \mathbf{x}_2 \\ \vdots \\ \mathbf{x}_P \end{bmatrix}, \quad \text{ただし} \mathbf{x}_p = \begin{bmatrix} x_{p1} &x_{p2} &\cdots &x_{pK} \end{bmatrix} \tag{B.4}\] とも表すことができます。
このように，ベクトルを「行列の一要素」として見る場合には，それぞれ列ベクトル（column vector: B.3 式の\(\mathbf{x}_k\)），行ベクトル（row vector: B.4 式の\(\mathbf{x}_p\)）とも呼ばれます。 あらゆる行列は，常に行ベクトルの集合とも列ベクトルの集合ともみなせるわけですが，どちらの見方をするかは行列の中身や計算の都合によってコロコロ変わります。
更にいうと，ベクトルや行列の縦横は自由に入れ替えることができます。 この操作を転置 (transpose) と呼び，本資料では転置されたベクトル（転置ベクトル）および行列（転置行列）は上付き添字（\(^{\top}\)）で表すことにします2。 例えば (B.1) 式のベクトルをそれぞれ転置すると， \[ \mathbf{x}^{\top} = \begin{bmatrix} x_1 & x_2 & \cdots & x_K \end{bmatrix} \qquad \mathbf{y}^{\top} = \begin{bmatrix} y_1 \\ y_2 \\ \cdots \\ y_K \end{bmatrix} \tag{B.5}\] となります。同様に，(B.2) 式の行列を転置したものも \[ \mathbf{X}^{\top} = \begin{bmatrix} x_{11} & x_{21} &\cdots & x_{P1} \\ x_{12} & x_{22} &\cdots & x_{P2} \\ \vdots & \vdots &\ddots & \vdots \\ x_{1K} & x_{2K} &\cdots & x_{PK} \end{bmatrix} \tag{B.6}\] となるわけです。
ベクトル・行列の転置は，多くの場合単に計算の都合上行っていることが多いので，あまり深い意味は考えなくても「単に行と列を入れ替えたもの」くらいに思っておけばひとまず大丈夫です。
B.1.3 データとベクトル・行列
そもそもなぜ多変量解析を線形代数で表す必要があるのでしょうか。 それは，データはそのまま行列として扱える形をしているためです。 データが行列の形で与えられている以上，線形代数は非常に都合が良いのです。 例えば本講義で使用するデータ（chapter04.rds）は，そのままでは2432行 \(\times\) 34列の行列とみなすこともできます。
また チャプター 1 では，Rのデータフレーム型オブジェクトが「列の集合」であると紹介しました。 したがって，Rでは基本的にはデータ行列は列ベクトルが横に並んだ形として扱っている，ということですね。
Rには，オブジェクトの型として，ベクトルを表すvector型と，行列を表すmatrix型があります。 データフレームを変換する場合には，as.vector()およびas.matrix()という関数が使えます。
Q1_1 Q1_2 Q1_3 Q1_4 Q1_5 Q1_6 Q1_7 Q1_8 Q1_9 Q1_10 Q1_11 Q1_12 Q1_13
1 5 4 3 4 4 2 3 3 3 3 4 4 3
2 5 4 5 2 5 5 4 4 4 3 6 6 6
3 2 4 5 4 4 4 5 4 5 2 5 3 4
4 3 4 6 5 5 4 4 3 2 2 2 4 4
Q1_14 Q1_15 Q1_16 Q1_17 Q1_18 Q1_19 Q1_20 Q1_21 Q1_22 Q1_23 Q1_24 Q1_25
1 4 4 3 4 2 2 3 3 1 3 4 4
2 4 3 3 3 3 5 5 4 5 4 3 4
3 4 5 4 5 4 2 3 4 5 5 5 5
4 4 4 2 5 2 4 1 3 4 4 3 2
[ reached getOption("max.print") -- omitted 2 rows ]ということで，dat[cols]を行列っぽく表すならば \[
\mathrm{dat} = \begin{bmatrix}
\mathbf{x}_1 & \mathbf{x}_2 & \mathbf{x}_3 & \cdots & \mathbf{x}_{25}
\end{bmatrix} = \begin{bmatrix}
5 & 4 & 3 & \cdots & 4 \\
5 & 4 & 5 & \cdots & 4 \\
2 & 4 & 5 & \cdots & 5 \\
\vdots & \vdots & \vdots & \vdots & \vdots \\
\end{bmatrix}
\] という感じになっているわけです。
matrix型オブジェクトから1行または1列だけを取り出したものは，Rではいずれも列（縦）ベクトルとして扱われます。 その上Rでは，縦ベクトルの要素であっても横並びに表示される点には注意が必要です。 つまりあるベクトルを表示したときに要素が横並びに表示されたからと言って，横ベクトルとは限らないということです。
1 2 3 4 5 6 7 8 10 11 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
5 5 2 3 5 1 5 3 5 3 2 2 3 3 3 2 3 3 2 6 6 5 3 6 5
28 29 30 31 32 33 34 36 37 38 39 40 41 43 44 45 46 47 48 49 50 51 52 53 54
5 5 3 6 5 6 5 2 6 6 6 6 6 6 2 5 6 2 5 6 6 6 6 4 3
[ reached getOption("max.print") -- omitted 2382 entries ]答えとしては「それがR言語の仕様だから」となってしまいます。
まず，Rのvector型は「オブジェクトが複数並んだもの」という意味の型なのですが，線形代数的な意味のベクトルとしては必ず縦ベクトルとして扱われるという性質があります。 例えばc()関数でくっつけて作成したベクトルも，自動的に縦ベクトルとなるのです。 一方横ベクトルは，Rでは1行P列の行列つまりmatrix型として表す必要があります。
これに加えて，Rには「型のドロップ」という特殊？な仕組みがあります。 これは，もとのオブジェクトよりも次元が小さくなる場合，小さくなった次元に合わせてオブジェクトの型が勝手に変換されるというものです。
……といってもよくわからないと思うので，具体例で説明しましょう。 matはmatrix型のオブジェクトでした。 「matrix型」は，行数と列数がある2次元のオブジェクトです。 次にここから1列だけを取り出した場合を考えてみます。 mat[, 1]は，値が縦に並んでいるので1次元のオブジェクトになります。 このとき，考え方によっては「2432行1列の行列」とみなすこともできそうなのですが，Rでは「値が1次元に並んでいるならvector型として扱おう」となり，結果的にmat[, 1]はvector型オブジェクトとなっているのです。 同様に，mat[1,]についても「1行34列の行列」としては扱われず，値が1次元に並んでいるためにvector型オブジェクトとして扱われ，さらにvector型オブジェクトには縦ベクトルしか存在しないので，結果的にこれも縦ベクトルとなっているのです。
型のドロップを避ける方法としては[]の中にdrop=FALSEを追記するというものがあります。
一見するとdrop=FALSEがないときとの違いがわかりませんが，出力の左に1という数字があることから判別可能です。 この1は「行列の1行目だよ」ということを意味しているため，確かにmatrix型（行ベクトル）になっていることがわかります。
また，t()という関数をかけると行列やベクトルを転置させることができます。
B.2 線形代数の基本演算
ここからは最低限知っておくべき演算をおさえていきます。 といっても高校数学のように実際に手計算で値を求められる必要はなく（できるに越したことはないですが），各操作がどんな計算を意味しているかをきちんと理解できればOKです。 とはいえ，その理解のために最初は少しでも手計算してみると良いのかもしれないので，計算については定義の後で簡単な数値例およびRでのやり方を載せておくことにします。 Rにおける線形代数の具体的な計算方法は，実際に本講義の内容を理解するだけなら知る必要はないのですが，いつの日か具体的な行列の手計算をする羽目になったときに役立つかもということでやり方も載せておきます。
B.2.1 足し算・引き算
大前提として，足し算および引き算は，同じサイズのベクトル・行列同士でしか行うことができません。 というのも，線形代数での足し算・引き算は，同じ位置の要素ごとの足し算・引き算をするためです。
ベクトルの足し算・引き算
単に同じ位置の要素ごとに足し算・引き算をするだけなので， \[ \mathbf{x}=\begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ \vdots \\ x_K \end{bmatrix}, \qquad \mathbf{y}=\begin{bmatrix} y_1 \\ y_2 \\ y_3 \\ \vdots \\ y_K \end{bmatrix} \] とすると， \[ \mathbf{x} + \mathbf{y}=\begin{bmatrix} x_1 + y_1 \\ x_2 + y_2 \\ x_3 + y_3 \\ \vdots \\ x_K + y_K \end{bmatrix} \] となります（横ベクトルどうしでも同じ要領でOK）。
例えば \[ \mathbf{x}=\begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix}, \qquad \mathbf{y}=\begin{bmatrix} 4 \\ 5 \\ 6 \end{bmatrix} \] のときには， \[ \mathbf{x} + \mathbf{y}=\begin{bmatrix} 1 + 4 \\ 2 + 5 \\ 3 + 6 \end{bmatrix} =\begin{bmatrix} 5 \\ 7 \\ 9 \end{bmatrix}, \qquad \mathbf{x} - \mathbf{y}=\begin{bmatrix} 1 - 4 \\ 2 - 5 \\ 3 - 6 \end{bmatrix} =\begin{bmatrix} -3 \\ -3 \\ -3 \end{bmatrix} \] ということです。
vector型オブジェクトを作るためにはc()関数が使えました。 ただしここでは，今後のことも考えて「3行1列の行列」として定義してみましょう。 Rでmatrix型オブジェクトを定義するためには，matrix()という関数を使います。
そして，足し算は普通に+記号を，引き算は-記号を使えばOKです。
行列の足し算・引き算
ベクトルのときと要領は全く同じです。
\[ \mathbf{X} = \begin{bmatrix} x_{11} & x_{12} &\cdots & x_{1K} \\ x_{21} & x_{22} &\cdots & x_{2K} \\ \vdots & \vdots &\ddots & \vdots \\ x_{P1} & x_{P2} &\cdots & x_{PK} \end{bmatrix}, \qquad \mathbf{Y} = \begin{bmatrix} y_{11} & y_{12} &\cdots & y_{1K} \\ y_{21} & y_{22} &\cdots & y_{2K} \\ \vdots & \vdots &\ddots & \vdots \\ y_{P1} & y_{P2} &\cdots & y_{PK} \end{bmatrix} \] とすると， \[ \mathbf{X} + \mathbf{Y} = \begin{bmatrix} x_{11} + y_{11} & x_{12} + y_{12} &\cdots & x_{1K} + y_{1K} \\ x_{21} + y_{21} & x_{22} + y_{22} &\cdots & x_{2K} + y_{2K} \\ \vdots & \vdots &\ddots & \vdots \\ x_{P1} + y_{P1} & x_{P2} + y_{P2} &\cdots & x_{PK} + y_{PK} \end{bmatrix} \] となります（引き算も同じなので省略）。
例えば \[ \mathbf{X}=\begin{bmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{bmatrix}, \quad \mathbf{Y}=\begin{bmatrix} 7 & 10 \\ 8 & 11 \\ 9 & 12 \end{bmatrix} \] のときには， \[ \begin{aligned} \mathbf{X} + \mathbf{Y}&=\begin{bmatrix} 1+7 & 4+10 \\ 2+8 & 5+11 \\ 3+9 & 6+12 \end{bmatrix} =\begin{bmatrix} 8 & 14 \\ 10 & 16 \\ 12 & 18 \end{bmatrix} \\ \mathbf{X} - \mathbf{Y}&=\begin{bmatrix} 1-7 & 4-10 \\ 2-8 & 5-11 \\ 3-9 & 6-12 \end{bmatrix} =\begin{bmatrix} -6 & -6 \\ -6 & -6 \\ -6 & -6 \end{bmatrix} \end{aligned} \] となります。
matrix()関数の引数nrowおよびncolを変えるだけで任意の行列を作成可能です。
そして，足し算は普通に+記号を，引き算は-記号を使えばOKです。
B.2.2 掛け算
ベクトル・行列は，スカラー（定数）との掛け算が可能です（足し算引き算はダメでしたが）。 この場合，ベクトルが座標空間上で矢印で表されたことを思い出すと，単に各要素をスカラー倍したら良い，というだけです。簡単ですね。
ベクトルとスカラーの掛け算
\[ \mathbf{x}=\begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ \vdots \\ x_K \end{bmatrix} \] のとき， \[ c\mathbf{x}=\begin{bmatrix} cx_1 \\ cx_2 \\ cx_3 \\ \vdots \\ cx_K \end{bmatrix} \] となります（横ベクトルの場合も同じ要領でOK）。
\[ \mathbf{x}=\begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} \] とすると， \[ 10\mathbf{x}=\begin{bmatrix} 10\times 1 \\ 10\times 2 \\ 10\times 3 \end{bmatrix} =\begin{bmatrix} 10 \\ 20\\ 30 \end{bmatrix} \] となります。
行列とスカラーの掛け算
ベクトルのときと全く同じですが念の為。
\[ \mathbf{X} = \begin{bmatrix} x_{11} & x_{12} &\cdots & x_{1K} \\ x_{21} & x_{22} &\cdots & x_{2K} \\ \vdots & \vdots &\ddots & \vdots \\ x_{P1} & x_{P2} &\cdots & x_{PK} \end{bmatrix} \] とすると， \[ c\mathbf{X} = \begin{bmatrix} cx_{11} & cx_{12} &\cdots & cx_{1K} \\ cx_{21} & cx_{22} &\cdots & cx_{2K} \\ \vdots & \vdots &\ddots & \vdots \\ cx_{P1} & cx_{P2} &\cdots & cx_{PK} \end{bmatrix} \] となります。
\[ \mathbf{X}=\begin{bmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{bmatrix} \] のとき， \[ 10\mathbf{X}=\begin{bmatrix} 10\times 1 & 10\times 4 \\ 10\times 2 & 10\times 5 \\ 10\times 3 & 10\times 6 \end{bmatrix} = \begin{bmatrix} 10 & 40 \\ 20 & 50 \\ 30 & 60 \end{bmatrix} \] となります。
ベクトル・行列どうしの掛け算
ここからが線形代数の厄介ポイントです。 とりあえず計算の仕方を紹介していきますが，なぜこんなことになってしまったのかはもう少し後で説明するので，今は頑張って理解しようとしてください。
掛け算を理解するために，まずは簡単な計算例から示します。 例えば \[ \mathbf{X}=\begin{bmatrix} 1 & 3 & 5 \\ 2 & 4 & 6 \end{bmatrix}, \quad \mathbf{Y}=\begin{bmatrix} 7 & 10 \\ 8 & 11 \\ 9 & 12 \end{bmatrix} \] の場合，行列の積\(\mathbf{XY}\)の各要素は以下のように求められます。
まず左上の(1,1)要素は，左側の行列（ここでは\(\mathbf{X}\)）の1行目と，右側の行列（\(\mathbf{Y}\)）の1列目の要素を順番にかけたものの合計になります。 すなわち，\((1\times 7) + (3\times 8) + (5\times 9)=76\)となります。
同様に，(1,2)要素は左側の行列（ここでは\(\mathbf{X}\)）の1行目と，右側の行列（\(\mathbf{Y}\)）の2列目の要素を順番にかけたものの合計です。 すなわち，\((1\times 10) + (3\times 11) + (5\times 12)=103\)となります。
このように行列の積の(\(i,j\))要素は，左側の行列の\(i\)行目と右側の行列の\(j\)列目の要素をそれぞれ左・上から順にかけたものの総和となります。 結果として，上の\(\mathbf{X}\)と\(\mathbf{Y}\)の積は \[ \begin{aligned} \mathbf{XY}&=\begin{bmatrix} 1 & 3 & 5 \\ 2 & 4 & 6 \end{bmatrix}\begin{bmatrix} 7 & 10 \\ 8 & 11 \\ 9 & 12 \end{bmatrix} \\ &= \begin{bmatrix} (1\times 7) + (3\times 8) + (5\times 9) & (1\times 10) + (3\times 11) + (5\times 12) \\ (2\times 7) + (4\times 8) + (6\times 9) & (2\times 10 )+ (4\times 11) + (6\times 12) \end{bmatrix} \\ &= \begin{bmatrix} 76 & 103 \\ 100 & 136 \end{bmatrix} \end{aligned} \] となるのです。
行列の積がこのように定義されている関係上，積が計算できるのは「左側の行列の列数」と「右側の行列の行数」が一致している場合に限られます。 また，積の行数と列数はそれぞれ「左側の行列の行数」と「右側の行列の列数」に一致します。
更に注意しておくべき点として，普通の掛け算のように\(\mathbf{XY}=\mathbf{YX}\)になるとは限りません。 実際に\(\mathbf{YX}\)を計算してみると， \[ \begin{aligned} \mathbf{YX}&=\begin{bmatrix} 7 & 10 \\ 8 & 11 \\ 9 & 12 \end{bmatrix}\begin{bmatrix} 1 & 3 & 5 \\ 2 & 4 & 6 \end{bmatrix} \\ &= \begin{bmatrix} (7\times 1) + (10\times 2) & (7\times 3) + (10\times 4) & (7\times 5) + (10\times 6) \\ (8\times 1) + (11\times 2) & (8\times 3) + (11\times 4) & (8\times 5) + (11\times 6) \\ (9\times 1) + (12\times 2) & (9\times 3) + (12\times 4) & (9\times 5) + (12\times 6) \end{bmatrix} \\ &= \begin{bmatrix} 27 & 61 & 95 \\ 30 & 68 & 106 \\ 33 & 75 & 117 \end{bmatrix} \end{aligned} \] となります。 上の例の場合，そもそも\(\mathbf{XY}\)と\(\mathbf{YX}\)は計算結果の行列のサイズすら異なるのですが，\(\mathbf{XY}\)と\(\mathbf{YX}\)のサイズが同じになる（2つの行列の行数と列数が同じ）場合であっても，多くの場合で掛け算の向きによって結果は変わってしまいます。 線形代数では，掛け算の順序が超重要なのです。
Rで実装
普通の掛け算として*記号を使った場合，要素ごとの掛け算（アダマール積と呼ばれます）になります。 ただしこれは，2つの行列のサイズが一致していないとエラーを返します。
線形代数的に行列の積を求めたい場合には，%*%という記号を使う必要があります。
B.2.3 連立方程式を行列で表す
掛け算がこんなややこしい形になっている理由は，そもそも線形代数が「連立方程式を解く」場面で生み出されたためらしいです。 そこで，簡単な連立方程式を行列の積によって表してみましょう。
以下のような連立方程式を考えます。 \[ \left\{ \begin{alignedat}{4} 2&a&+&3&b&=7 \\ &a&+&&b&=2 \end{alignedat} \right. \] この連立方程式の左辺は，行列の積が先ほど紹介したように計算されると定義されているならば， \[ \begin{bmatrix} 2a + 3b \\ a + b \end{bmatrix} = \begin{bmatrix} 2 & 3 \\ 1 & 1 \end{bmatrix}\begin{bmatrix} a \\ b \end{bmatrix} \] というように，行列の積で表せるように分解することができます。 すなわち，行列の積を先ほど説明したように定義することで，連立方程式の左辺は「係数の行列」と「求めたい未知数の行列（ベクトル）」に分解できるわけです。 そして右辺も含めて連立方程式全体を行列で表していくと， \[ \begin{bmatrix} 2 & 3 \\ 1 & 1 \end{bmatrix}\begin{bmatrix} a \\ b \end{bmatrix} = \begin{bmatrix} 7 \\ 2 \end{bmatrix} \tag{B.7}\] となります。 ここで，左辺の係数行列を\(\mathbf{X}\)，左辺の未知数ベクトルを\(\boldsymbol{\theta}\)，右辺のベクトルを\(\mathbf{Y}\)とそれぞれ置くと，(B.7)式はシンプルに \[ \begin{alignedat}{2} &&\begin{bmatrix} 7 \\ 2 \end{bmatrix} &= \begin{bmatrix} 2 & 3 \\ 1 & 1 \end{bmatrix}\begin{bmatrix} a \\ b \end{bmatrix} \\ \longrightarrow &\quad&\mathbf{Y} &= \mathbf{X}\boldsymbol{\theta} \end{alignedat} \tag{B.8}\] というように，もともと複数あった方程式をまるでひとつの式であるかのように表すことができました。 この表記のポイントは，各ベクトル・行列のサイズを適切に設定したならば，連立方程式の数と未知数の数がいくつであっても，常に同じ式\(\mathbf{Y} = \mathbf{X}\boldsymbol{\theta}\)で表せるという点です。 これによって，数理的な説明が非常にラクに一般化できるようになりました。
とはいえここまでの説明はあくまでも連立方程式の話です。 多変量解析においてこのような表記がどう役に立つのか，意味が分からないかもしれません。 ですがこのような構造（モデル式）は，多変量解析では様々な場面でお目にかかるものです。 例えば回帰分析では，\(\mathbf{Y}, \mathbf{X}, \boldsymbol{\theta}\)はそれぞれ「被説明変数ベクトル」，「説明変数の行列」，「回帰係数のベクトル」に相当します。 同様に因子分析では\(\mathbf{Y}, \mathbf{X}, \boldsymbol{\theta}\)は「観測変数の行列」，「因子得点の行列」，「因子負荷の行列」に対応しているのです。 多変量解析では，たびたびこのようにデータのベクトル・行列を（潜在変数または観測変数の）2つの行列の積に分解して表現することが行われているのです。
話を連立方程式に戻すと，あとはこの式を\(\boldsymbol{\theta} =\) (なにか)の形になるように変形させていけば，解を求められそうな気がしてきますね。 直感的には，両辺を\(\mathbf{X}\)で割るような操作ができれば解が求められそうです。 別の言い方をすると，行列の逆数にあたるものをかけてあげることでも目的は達成できそうです。
B.2.4 逆行列（割り算に相当するもの）
行列の逆数にあたるものは，逆行列 (inverse of a matrx) と呼ばれます。 逆行列を考える前に，逆数について思い出してみましょう。 例えばスカラー\(x\)の逆数は，\(\frac{1}{x}\)または\(x^{-1}\)と表すことができました。 これは，言葉で言うならば「かけると1になる数」ということです。
同じように考えると，ある行列に対する逆行列は「かけると1に相当する行列になる行列」ということができそうです。 では，行列における「1に相当する」とは何なのでしょうか。
単位行列
「1に相当する」行列は，単位行列 (unit matrix) と呼ばれます。 例えば\(2\times 2\)単位行列は \[ \mathbf{I}=\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \] という形をしています。 単位行列は，慣習的に\(\mathbf{I}\)で表されます3。
より一般化して表すと，\(k \times k\)単位行列は \[ \mathbf{I}=\begin{bmatrix} 1 & 0 & 0 & \cdots & 0\\ 0 & 1 & 0 & \cdots & 0\\ 0 & 0 & 1 & \cdots & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & 0 & \cdots & 1\\ \end{bmatrix} \] という形をしています。 すなわち，単位行列とは「行数と列数が同じ行列のなかでも，対角成分が1で，残りの非対角成分がすべて0の行列」です。
実際にいくつか計算してみるとすぐに分かるのですが，単位行列はどんな行列に右からかけても左からかけても（積が計算できる限りは）必ずもとの行列と全く同じになります。 これは，特定の数字に1をかけてももとの数字から変わらないことと意味的には全く同じであり，単位行列が「1に相当する」と言われてる理由です。
単位行列の掛け算の一例を見てみましょう。 \[ \mathbf{X}=\begin{bmatrix} 1 & 3 & 5 \\ 2 & 4 & 6 \end{bmatrix} \] という行列に対して，右から掛け算ができる\(3\times 3\)単位行列をかけてみると， \[ \mathbf{XI}=\begin{bmatrix} 1 & 3 & 5 \\ 2 & 4 & 6 \end{bmatrix}\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}=\begin{bmatrix} 1 & 3 & 5 \\ 2 & 4 & 6 \end{bmatrix} = \mathbf{X} \] と，確かにもとの行列\(\mathbf{X}\)と同じになることがわかります。
ということで，行列\(\mathbf{X}\)に対する逆行列を（通常の逆数と同じように）\(\mathbf{X}^{-1}\)と表すと，これは「\(\mathbf{XX}^{-1}=\mathbf{X}^{-1}\mathbf{X}=\mathbf{I}\)となるような行列」と定義することができます。
逆行列を求める
逆行列\(\mathbf{X}^{-1}\)を手計算で求める方法には，掃き出し法や余因子法といったものがありますが，多変量解析においては手計算をすることはまあないので説明は省略します。 また，\(2\times 2\)行列に対する逆行列には公式があることが知られており，一応手計算も簡単に可能です（この講義の範囲で言えば覚える必要はないかも）。 公式によれば， \[ \mathbf{X}=\begin{bmatrix} a & b \\ c & d \end{bmatrix} \] とすると，逆行列は \[ \mathbf{X}^{-1}=\frac{1}{ad-bc} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix} \] となります。 例えば，先程の(B.7)式における係数の行列 \[ \begin{bmatrix} 2 & 3 \\ 1 & 1 \end{bmatrix} \] に対する逆行列は， \[ \frac{1}{2-3} \begin{bmatrix} 1 & -3 \\ -1 & 2 \end{bmatrix}=\begin{bmatrix} -1 & 3 \\ 1 & -2 \end{bmatrix} \] となります。実際に\(\mathbf{X}\)と\(\mathbf{X}^{-1}\)を掛けてみると， \[ \begin{aligned} \mathbf{X}\mathbf{X}^{-1}&=\begin{bmatrix} 2 & 3 \\ 1 & 1 \end{bmatrix}\begin{bmatrix} -1 & 3 \\ 1 & -2 \end{bmatrix}\\ &= \begin{bmatrix} (2\times -1) + (3\times 1) & (2\times 3) + (3\times -2) \\ (1\times -1) + (1\times 1) & (1\times 3) + (1\times -2) \end{bmatrix}\\ &= \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \end{aligned} \] となり，確かに積が単位行列となっていることがわかります。 また，逆行列を左からかけたとしても \[ \begin{aligned} \mathbf{X}^{-1}\mathbf{X}&=\begin{bmatrix} -1 & 3 \\ 1 & -2 \end{bmatrix}\begin{bmatrix} 2 & 3 \\ 1 & 1 \end{bmatrix}\\ &= \begin{bmatrix} (-1\times 2) + (3\times 1) & (-1\times 3) + (3\times 1) \\ (1\times 2) + (-2\times 1) & (1\times 3) + (-2\times 1) \end{bmatrix}\\ &= \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \end{aligned} \] と，やはり積は単位行列になりました。
なお，Rでは逆行列を求める関数としてsolve()という関数が用意されています。
B.2.5 連立方程式を線形代数で解く
それでは，逆行列・単位行列を用いて(B.7)式を変換してみましょう。 といってもやることは簡単で，両辺に係数行列の逆行列を左からかけてあげるだけです。 \[ \begin{aligned} (\mathbf{X}^{-1}\mathbf{X}\boldsymbol{\theta} &= \mathbf{X}^{-1}\mathbf{Y}) \\ \begin{bmatrix} -1 & 3 \\ 1 & -2 \end{bmatrix}\begin{bmatrix} 2 & 3 \\ 1 & 1 \end{bmatrix}\begin{bmatrix} a \\ b \end{bmatrix} &= \begin{bmatrix} -1 & 3 \\ 1 & -2 \end{bmatrix}\begin{bmatrix} 7 \\ 2 \end{bmatrix} \end{aligned} \] を整理すると，左辺は単位行列が消せるため， \[ \begin{aligned} (\boldsymbol{\theta} &= \mathbf{X}^{-1}\mathbf{Y}) \\ \begin{bmatrix} a \\ b \end{bmatrix} &= \begin{bmatrix} -1 \\ 3 \end{bmatrix} \end{aligned} \] というようにして，連立方程式の解を求めることができるのでした。
実は，逆行列はどんな行列にも存在しているわけではありません。 まず，逆行列は右からかけても左からかけても計算結果が単位行列\(\mathbf{I}\)になる必要があるため，行数と列数が同じ行列（正方行列）にしか存在しません。
それだけでなく，正方行列の中にも逆行列が存在しないものがあります。 例えば以下の行列 \[ \mathbf{X}=\begin{bmatrix} 1 & 2 \\ 3 & 6 \end{bmatrix} \] には，\(\mathbf{XX}^{-1}=\mathbf{I}\)となるような逆行列\(\mathbf{X}^{-1}\)は存在しません。
「逆行列がない」とはどんな状態なのでしょうか。 試しに\(\mathbf{X}\)を係数に持つような適当な連立方程式を考えると，例えば \[ \left\{ \begin{aligned} a+2b&=3 \\ 3a+6b&=9 \end{aligned} \right. \] のようなものが思いつきます。 この連立方程式をよく見ると，2つめの式は，単に1つめの式の両辺を3倍したものになっています。 したがって，これは連立方程式に見えて1つの方程式しかないのと同じことを意味していると言えます。 その結果，この連立方程式では解が1つに定まりません。
同様に，係数は同じで右辺が異なる以下のような連立方程式でも良いでしょう。 \[ \left\{ \begin{aligned} a+2b&=1 \\ 3a+6b&=5 \end{aligned} \right. \] このように，連立方程式の2つ目の式の右辺の値が，1つ目の式の3倍以外の値になっている場合は，これを満たす解は無い状態になります。 いずれにしても，この係数行列\(\mathbf{X}\)が使われている時点で，連立方程式が「唯一の解」を持つことはないのです。
先ほど，連立方程式の解を求める際には両辺に逆行列をかけていました。 そのため，「逆行列が存在しないこと」と「連立方程式の解が1つに決まらないこと」は同じことであると言えるのです。
ある行列に逆行列が存在しているとき，その行列は正則であるという言い方をします。 行列が正則でなくなる最もシンプルなケースは，上記の例のようにある行または列が，他の行または列のスカラー倍になっている場合です。 同様に，他の行または列のスカラー倍の重み付け和になっている場合も逆行列は存在しなくなってしまいます。 これは，データ行列で言えば「ある説明変数\(x_1\)が別の説明変数\(x_2\)の倍数になっている」状態などに相当します。 このとき，\(x_1\)と\(x_2\)はどちらかがあれば十分な状態なので，一方の変数はなくても良いと言えます。
このように，逆行列が存在するためにはデータ行列の変数がすべて「他の変数では説明できないユニークな成分を持っている」ことが求められるのです。 （これは，回帰分析の多重共線性の概念に直接結びつく話です。）
B.3 データ分析に登場するあれこれ
本当は，線形代数の幾何学的な意味などについても知っておくとデータの見通しが良くなったりはするのですが，そんな余裕もないので，ここからはデータ分析（多変量解析）において見られるいくつかの行列・ベクトルの話を列挙していきます。
B.3.1 ベクトルの積
あるベクトル \[ \mathbf{x} = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_K \end{bmatrix} \] を「\(K\)行1列の行列」としてみると，このベクトル自身どうしの積は以下の2種類考えることができます。
まず，左に転置ベクトルをおいた積（内積）は \[ \mathbf{x}^{\top}\mathbf{x} = \begin{bmatrix} x_1 & x_2 & \cdots & x_K \end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_K \end{bmatrix} = \sum_{k=1}^{K}x_k^2 \] というように，ベクトルの各要素の二乗和を意味します。 これはデータ分析においては，例えば\(\mathbf{x}\)を平均値からの偏差ベクトル \[ \mathbf{x} = \begin{bmatrix} x_1-\bar{x} \\ x_2-\bar{x} \\ \vdots \\ x_K-\bar{x} \end{bmatrix} \] とした際に，分散が \[ \frac{1}{n}\mathbf{x}^{\top}\mathbf{x} \tag{B.9}\] と表せる，といったような形で現れます。 これ以外にも，「二乗和を取る」という操作はデータ分析でちょくちょく出現しますが，線形代数的にはこのように表すことができるのです。
一方で，右に転置ベクトルをおいた積は \[ \begin{aligned} \mathbf{x}\mathbf{x}^{\top} &= \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_K \end{bmatrix}\begin{bmatrix} x_1 & x_2 & \cdots & x_K \end{bmatrix} \\ &= \begin{bmatrix} x_1^2 & x_1x_2 & \cdots & x_1x_K \\ x_2x_1 & x_2^2 & \cdots & x_2x_K \\ \vdots & \vdots & \ddots & \vdots \\ x_Kx_1 & x_Kx_2 & \cdots & x_K^2 \end{bmatrix} \end{aligned} \] という形になります。 この形は，因子分析において観測変数間の相関行列を表現する際などに出現する形です。
また，異なるベクトル \[ \mathbf{w} = \begin{bmatrix} w_1 \\ w_2 \\ \vdots \\ w_K \end{bmatrix} \] との積\(\mathbf{w}^{\top}\mathbf{x}\)は，\(\mathbf{x}\)の各要素を\(\mathbf{w}\)によって重みづけた和を意味します。 これは，例えば回帰分析において「説明変数\(\times\)回帰係数の和」といった形で出現したりします。
B.3.2 分散共分散行列
データフレームの全変数の組み合わせに対して求めた共分散を行列の形式で表したものは，分散共分散行列 (variance-covariance matrix) と呼ばれます。 なお「変数\(x\)の分散」は，「変数\(x\)と変数\(x\)の共分散」と同じものを意味しているため，単に共分散行列と呼ばれることもあります。
分散共分散行列の\((i,j)\)要素は，データフレーム内の\(i\)番目の変数と\(j\)番目の変数の共分散を表しています。 そのため，分散共分散行列では
- 行数・列数がともに「データフレームの変数の数」の正方行列である
- 対角成分は各変数の分散を表す
- 非対角成分は各変数のペアの共分散を表す
- (\(i,j\))成分と(\(j,i\))成分は必ず同じ値になる
という性質があります。特に最後の性質によって，分散共分散行列は転置しても全く変わらないということが言えます。 このような行列を対称行列 (symmetric matrix)と呼びます。 また，分散共分散行列は基本的には逆行列が存在するため，多変量解析においても様々な形で利用されています。
Rでは，cov()という関数を使うことで分散共分散行列が求められます。
B.3.3 相関行列
分散共分散行列と同じように，各変数間の相関係数を要素に持つ行列を相関行列 (correlation matrix) と呼びます。 多くの性質は分散共分散行列と同じで，
- 行数・列数がともに「データフレームの変数の数」の正方行列である
- 対角成分は1（同じ変数どうしの相関係数なので）
- 非対角成分は各変数のペアの相関係数を表す
- (\(i,j\))成分と(\(j,i\))成分は必ず同じ値になる
- 基本的には逆行列が存在する
といった性質を持っています。これも多変量解析では様々な方法で利用されています。
Rでは，cor()という関数が用意されています。
B.3.4 対角行列
対角行列 (diagonal matrix) とは，対角成分のみが0以外の値で，非対角成分がすべて0の行列のことです。 もしも分散共分散行列に対角行列を仮定すると，これはすべての変数が無相関であることを意味します。
実際に，因子分析においては一般的に，各観測変数に対する独自因子（または誤差）の分散共分散行列には対角行列が置かれます。 ……という感じで，無相関の変数間の分散共分散行列として対角成分が用いられることがあります。
Rでは，diag()という関数を使うと簡単に対角行列を作ることができます。
（他に重要な話を書き忘れていたらあとで追加しておくかもしれません）