3 データの前処理

abstract

データを分析できる状態にするための前処理（欠測値の削除・適当な回答の検出・逆転項目の処理）の考え方およびRでの実行方法を紹介しています。

チャプター 2 では，データを読み込み，元データのレベルでのチェックを行いました。ただ，まだデータを確認しただけで，このまま分析しても思ったような結果が得られない可能性があります。というのもデータには多かれ少なかれノイズ（ゴミ）が混ざっており，そのまま残しておくと今後の分析に良くない影響を与えかねません。ということで今回は主にデータの前処理を行っていきたいと思います。

データの読み込み

まずは前回保存したデータを読み込みましょう。 .rdsファイルを読み込む場合には，readRDS()関数を使います。

コード 3.1: .rdsファイルを読み込む

# 保存したときのオブジェクト名(dat)と同じである必要はありません
dat <- readRDS("chapter02.rds")

もしsave()やsave.image()関数で保存した.rdataファイルを読み込みたい場合には，load()関数を使います。

コード 3.2: まとめて環境を読み込む

load("chapter02_all.rdata")

load()関数では，代入の記号（<-）を使用していません。これは，save()関数で保存した.rdataファイルにはオブジェクトが中身から名前まで丸ごと保存されており，load()関数はそれを丸ごと読み込んでいるためです。一方saveRDS()関数で保存した場合にはオブジェクトの中身だけが保存されるため，保存前と別の名前をあてても問題ないわけです。そういった理由から，保存する際の拡張子を.rdsと.rdataと使い分けています（と私は思っています）。

3.1 欠測値の処理

はじめに無回答の処理の仕方について少し説明します。一般的に分析の際には，無回答は欠測値 (missing value) として扱われます。テクニカルな話をすると欠測値には以下の3つのタイプがあり，そのタイプに応じた対処が求められます（Schafer & Graham, 2002）。ここでは，「体重」を尋ねた質問への無回答を例に考えてみましょう。

MCAR: Missing Completely At Random とは，欠測値が完全にランダムに発生している状態です。簡単にいえばたまたま体重を記入し忘れた，という場合や明らかに異常値であるためにデータが使えない場合にはMCARとして扱うことが出来ます。
MAR: Missing At Random とは，欠測値がその変数以外に関連して発生している状態です。体重で言えば，女性の方が体重を答えるのをためらう傾向が強いと思われるので，「女性の方が体重の欠測が多い」と考えられる場合はMARとして扱います。名前に”At Random”と入っているのが少し違和感かもしれませんが，MARでは一応欠測の発生は確率的に発生する（ただし発生確率が他の変数によって変わる）と考えています。
MNAR: Missing Not At Random とは，欠測値がその変数自体に関連して発生している状態です。体重で言えば，肥満傾向の人のほうが体重を答えるのをためらう傾向が強いと思われるので，「肥満の人の方が体重の欠測が多い」と考えられる場合や，体重計のスペック的に「測定不能」となってしまった場合はMNARとして扱います。

具体的な対処法まで話すと長くなってしまうので省略しますが¹，簡単に言うとMNARでなければ統計的に欠測値を埋める方法があると考えて良さそうです²。したがって，特定の属性について欠測値が多くなっていてもバイアスを補正した推定が可能となるわけです。ということで，質問紙調査を行う段階で，MNARが発生しそうなセンシティブな項目などには特段の注意が必要となります。

実際にデータで見られた欠測がどのタイプなのかについては，ドメイン知識やデータの状況などによって総合的に判断する必要があります。先程説明したように，同じ「体重」という変数をとっても，その背後に異なるメカニズムを想像するだけでどのタイプにも該当しそうでした。というわけで，欠測値のタイプを判断するための統計的な指標は今のところほぼ存在しないと思います³。ちなみに今回のデータにおける欠測値を考えてみると，

心理尺度の25項目に関する欠測値はMCARと考えてもよさそう
educationの欠測はMNARのような気もするけど…

という感じでしょうか。とりあえず心理尺度の25項目に関してはMCARとみなして，以後の分析では「25項目の中には欠測値がない人」だけを残して使用したいと思います。今回は全体で2800人いるので，多少減っても問題ないでしょう。

ただし，一つでも欠測値がある人を除外する場合は，事前に項目ごとの無回答率を確認しておいたほうが良いです。もしかしたら特定の項目が回答しにくくて無回答を誘発していたり，後半の設問ほど無回答率が高くなっていたり…ということがあるかもしれません。こうした状態を無視して機械的に除外してしまうと，「特定の項目に回答できる人」や「飽きっぽくない・回答が早い人」が多めに残ってしまい，何らかの偏りが発生してしまう可能性もあります。

Rでは欠測はNAとして扱われています。そのため，列ごとにNAとなっているデータの数（割合）を計算することで無回答率が算出できそうです。ちょっと厄介なのは，NAは比較演算では特殊な挙動をする，という点です。「NAと一致するか」はシンプルに考えると等号(==)を用いて以下のように書けそうですが，実際にはそうはいきません。

コード 3.3: 等号の演算子を使ってNAかどうかを判定すると

c(1, NA, 3, NA, 5, 6) == NA

[1] NA NA NA NA NA NA

このように，NAとの比較は「判断不能」的な感じで結果もNAになってしまいます。代わりにRには，NAかどうかを判断する関数として，is.na()という関数が用意されているのでこれを使いましょう⁴。 is.na()関数は，引数に与えたものに関して，NAであればTRUE，そうでなければFALSEを返します。ベクトルや行列・データフレームを与えた場合はその要素ごとにTRUE/FALSEを出してくれます。

コード 3.4: [is.na] NAであるかを判定する

is.na(c(1, NA, 3, NA, 5, 6))

[1] FALSE  TRUE FALSE  TRUE FALSE FALSE

これを使えば，それぞれの値が「NAであるか」を判定できるようになります。あとはNAの数を数えるだけです。

is.na()関数の出力はlogical型（TRUE/FALSEしかとらない）のベクトルなのですが，実は内部的にはTRUEは1，FALSEは0としても扱われます。

コード 3.5: 1列まるごとis.na()

is.na(dat[, "education"])

 [1]  TRUE  TRUE  TRUE  TRUE  TRUE FALSE  TRUE FALSE FALSE  TRUE FALSE
[12]  TRUE  TRUE  TRUE FALSE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
[23] FALSE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE  TRUE FALSE FALSE
[34]  TRUE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE
[45] FALSE FALSE FALSE FALSE FALSE FALSE
 [ reached getOption("max.print") -- omitted 2750 entries ]

コード 3.6: is.na()の出力を強制的に数値に変換してみる

as.numeric(is.na(dat[, "education"]))

  [1] 1 1 1 1 1 0 1 0 0 1 0 1 1 1 0 1 1 1 1 1 1 1 0 0 0 0 0 1 0 0 1 0
 [33] 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 [65] 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0
 [97] 0 0 0 0
 [ reached getOption("max.print") -- omitted 2700 entries ]

そのため，is.na()の出力は何も考えずにそのままmean()に突っ込むことで，TRUEの割合（無回答率）がカウントできます。同様に，sum()をとればTRUEの人数（この場合欠測の人数）をカウントすることも可能です。

コード 3.7: １項目の欠測（無回答）率を出す

mean(is.na(dat[, "education"]))

[1] 0.07964286

コード 3.8: １項目の欠測人数を出す

sum(is.na(dat[, "education"]))

[1] 223

ということで，あとはこれを全項目に対して適用していけば良いのですが，下のように全部書いていてはキリがありません。今回はIDを除いて28項目なのでまだなんとかなりますが，数百項目になったらどうしましょう。

コード 3.9: 変数ごとに愚直に書くなら

mean(is.na(dat[, "Q1_1"]))
mean(is.na(dat[, "Q1_2"]))
mean(is.na(dat[, "Q1_3"]))
mean(is.na(dat[, "Q1_4"]))
############# (中略) ##############
mean(is.na(dat[, "Q1_25"]))
mean(is.na(dat[, "age"]))
mean(is.na(dat[, "gender"]))
mean(is.na(dat[, "education"]))

このような場合に備えて「一気に複数の列（または行）に同じ処理を施す方法」を紹介します。 apply()関数は，データフレーム・行列・多次元配列について，指定した次元（行または列）にそれぞれ同じ関数を適用するという関数です。 …よくわからないと思うので実際にやってみましょう。まずは以下のコードと出力を見てみてください。

コード 3.10: apply()のキホン

apply(dat, 2, head)

     ID Q1_1 Q1_2 Q1_3 Q1_4 Q1_5 Q1_6 Q1_7 Q1_8 Q1_9 Q1_10 Q1_11 Q1_12
[1,]  1    2    4    3    4    4    2    3    3    4     4     3     3
[2,]  2    2    4    5    2    5    5    4    4    3     4     1     1
[3,]  3    5    4    5    4    4    4    5    4    2     5     2     4
     Q1_13 Q1_14 Q1_15 Q1_16 Q1_17 Q1_18 Q1_19 Q1_20 Q1_21 Q1_22 Q1_23
[1,]     3     4     4     3     4     2     2     3     3     6     3
[2,]     6     4     3     3     3     3     5     5     4     2     4
[3,]     4     4     5     4     5     4     2     3     4     2     5
     Q1_24 Q1_25 gender education age
[1,]     4     3      1        NA  16
[2,]     3     3      2        NA  18
[3,]     5     2      2        NA  17
 [ reached getOption("max.print") -- omitted 3 rows ]

head(dat)のときと同じような結果になりました。この時，裏では図 3.1 のような処理が行われています。つまりhead(dat[,1])，head(dat[,2])，…をという感じで列ごとに同じ関数を適用し，その結果をまとめているのです。

図 3.1: apply(dat, 2, head)の挙動

apply()は基本的に3つの引数からなります。apply(X, MARGIN, FUN)

X: 関数を適用する元データです。
MARGIN: どの次元に関して，それぞれ関数を適用するかを指します。数字はデータフレームにおける要素の指定[ , ]のときの順番と同じです。したがってMARGIN = 1の場合は行ごと，MARGIN = 2の場合は列ごとに関数を適用します。
FUN: どの関数を適用するかです。もしその関数が別の引数を取る場合は，この後に引数を続けて書いていきます。

では，当初の目的である「datの列ごとにNAの割合を出したい」場合にはどうしたら良いでしょうか。引数を一つずつあてはめていくと，Xにはis.na(dat)を，MARGINには2(列ごと)を，FUNにはmeanが入れば良さそうです。

コード 3.11: まずはデータフレームにis.na()

is.na(dat)

           ID  Q1_1  Q1_2  Q1_3  Q1_4  Q1_5  Q1_6  Q1_7  Q1_8  Q1_9
   [1,] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
   [2,] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
   [3,] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
        Q1_10 Q1_11 Q1_12 Q1_13 Q1_14 Q1_15 Q1_16 Q1_17 Q1_18 Q1_19
   [1,] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
   [2,] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
   [3,] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
        Q1_20 Q1_21 Q1_22 Q1_23 Q1_24 Q1_25 gender education   age
   [1,] FALSE FALSE FALSE FALSE FALSE FALSE  FALSE      TRUE FALSE
   [2,] FALSE FALSE FALSE FALSE FALSE FALSE  FALSE      TRUE FALSE
   [3,] FALSE FALSE FALSE FALSE FALSE FALSE  FALSE      TRUE FALSE
 [ reached getOption("max.print") -- omitted 2797 rows ]

コード 3.12: 各項目（列）の無回答（NA）率を確認

apply(is.na(dat), 2, mean)

         ID        Q1_1        Q1_2        Q1_3        Q1_4 
0.000000000 0.005714286 0.009642857 0.009285714 0.006785714 
       Q1_5        Q1_6        Q1_7        Q1_8        Q1_9 
0.005714286 0.007500000 0.008571429 0.007142857 0.009285714 
      Q1_10       Q1_11       Q1_12       Q1_13       Q1_14 
0.005714286 0.008214286 0.005714286 0.008928571 0.003214286 
      Q1_15       Q1_16       Q1_17       Q1_18       Q1_19 
0.007500000 0.007857143 0.007500000 0.003928571 0.012857143 
      Q1_20       Q1_21       Q1_22       Q1_23       Q1_24 
0.010357143 0.007857143 0.000000000 0.010000000 0.005000000 
      Q1_25      gender   education         age 
0.007142857 0.000000000 0.079642857 0.000000000

educationの無回答率が0.079642857，つまりおよそ7.96%とやや高いですが，25項目中には無回答率の高い項目はなかったので，予定通り進めていきます。

欠測値があるレコードを取り除く関数としてはna.omit()というものがあります。ですがこの関数は一つでも欠測値がある行は全て除外するため，na.omit(dat)としてしまうとeducationがNAの人（つまり最終学歴を答えることに抵抗がある層）もごっそりと抜け落ちてしまいます。今は25項目の中に欠測がある人だけ取り除きたいので，ここではsubset()に適切な条件式を与えることで目的を達成していきましょう。材料は以下の関数たち＋is.na()＋apply()です。

コード 3.13: all(): 全てTRUEであるかどうかを判断する

# 与えたものが全てTRUEであればTRUEを返します。
all(c(TRUE, TRUE, TRUE))

[1] TRUE

# 一つでもFALSEがあればFALSEを返します。
all(c(TRUE, FALSE, TRUE))

[1] FALSE

コード 3.14: paste0(): 与えられたcharacter型を結合する

paste0("This ", "is ", "a pen.")

[1] "This is a pen."

# ベクトルを与えた場合，ベクトルの各要素に対して結合を行います。
# 大量の列名の指定に使えます。
paste0("No.", 1:10)

 [1] "No.1"  "No.2"  "No.3"  "No.4"  "No.5"  "No.6"  "No.7"  "No.8" 
 [9] "No.9"  "No.10"

これらを組み合わせると，以下のようにして目的を達成できます。最後の結果をdatに代入するのを忘れないように気をつけてください。

コード 3.15: 部分的に欠測が無いデータを残す手順1

# まず"Q1_1", "Q1_2", ...という文字列のベクトルを作る
cols <- paste0("Q1_", 1:25)
cols # 結果の表示

 [1] "Q1_1"  "Q1_2"  "Q1_3"  "Q1_4"  "Q1_5"  "Q1_6"  "Q1_7"  "Q1_8" 
 [9] "Q1_9"  "Q1_10" "Q1_11" "Q1_12" "Q1_13" "Q1_14" "Q1_15" "Q1_16"
[17] "Q1_17" "Q1_18" "Q1_19" "Q1_20" "Q1_21" "Q1_22" "Q1_23" "Q1_24"
[25] "Q1_25"

コード 3.16: 部分的に欠測が無いデータを残す手順2

# 25列について，各要素がNAかどうかを判定した（is.na）データフレームを作る
# !を使っているので，NAならばFALSE，値が入っていればTRUEになっている点に注意
dat_not_na <- !is.na(dat[, cols])
dat_not_na # 結果の表示

         Q1_1  Q1_2  Q1_3  Q1_4  Q1_5  Q1_6  Q1_7  Q1_8  Q1_9 Q1_10
   [1,]  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
   [2,]  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
   [3,]  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
   [4,]  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
        Q1_11 Q1_12 Q1_13 Q1_14 Q1_15 Q1_16 Q1_17 Q1_18 Q1_19 Q1_20
   [1,]  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
   [2,]  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
   [3,]  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
   [4,]  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
        Q1_21 Q1_22 Q1_23 Q1_24 Q1_25
   [1,]  TRUE  TRUE  TRUE  TRUE  TRUE
   [2,]  TRUE  TRUE  TRUE  TRUE  TRUE
   [3,]  TRUE  TRUE  TRUE  TRUE  TRUE
   [4,]  TRUE  TRUE  TRUE  TRUE  TRUE
 [ reached getOption("max.print") -- omitted 2796 rows ]

コード 3.17: 部分的に欠測が無いデータを残す手順3

# 25列について，各要素がNAかどうかを判定した（is.na）データフレームを作る
# !を使っているので，NAならばFALSE，値が入っていればTRUEになっている点に注意
# 行方向にapplyを適用，一つでもNAがある場合はFALSEを返している
no_missing <- apply(dat_not_na, 1, all)
no_missing # 結果の表示

 [1]  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE FALSE  TRUE  TRUE
[12] FALSE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
[23]  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
[34]  TRUE FALSE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE FALSE  TRUE  TRUE
[45]  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
 [ reached getOption("max.print") -- omitted 2750 entries ]

コード 3.18: 部分的に欠測が無いデータを残す手順4

# no_missingがTRUEの人だけをsubsetしている
dat <- subset(dat, no_missing)

もちろん，上記の処理を全て1行にまとめてdat <- subset(dat,apply(!is.na(dat[,paste0("Q1_",1:25)]),1,all))なんて書いてもOKです。でも読みにくいですねェ⁵。

きちんとNAがなくなっていることを確認するために，再度各列のNAの割合（または個数）をカウントしてみましょう。 Q1_1からQ1_25が全て0になっていればOKです。

コード 3.19: 改めて無回答（NA）率を確認

apply(is.na(dat), 2, mean)

        ID       Q1_1       Q1_2       Q1_3       Q1_4       Q1_5 
0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 
      Q1_6       Q1_7       Q1_8       Q1_9      Q1_10      Q1_11 
0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 
     Q1_12      Q1_13      Q1_14      Q1_15      Q1_16      Q1_17 
0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 
     Q1_18      Q1_19      Q1_20      Q1_21      Q1_22      Q1_23 
0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 
     Q1_24      Q1_25     gender  education        age 
0.00000000 0.00000000 0.00000000 0.08210181 0.00000000

最後に，欠測値を除外した後のデータフレームのサイズを確認しておきましょう。上で紹介したstr()でも行数は出してくれるのですが，ここではまた別の方法で確認してみます。

コード 3.20: dim(): データフレームのサイズを確認

dim(dat)

[1] 2436   29

コード 3.21: nrow(): データフレームの行数を確認

# 列数を見たい場合はncol()
nrow(dat)

[1] 2436

nrow()関数は，例えば「データフレームの各行に順番に何か処理をしたい」という場合に，1:nrow(dat)という形で「行数だけの長さの整数ベクトル」を作ったりする場合に有用です。この方法ならば，データのサイズが変わったとしてもコードを修正する必要が無い点がおすすめポイントです。また，ncol()は，一番右の列を取り出したい時なんかにも使えます。というように，nrow()およびncol()はところどころ使うことがあると思うので覚えておきましょう。

3.2 適当な回答を除外する

調査においては，全ての回答者が必ず誠実に回答してくれるとは限りません。特にウェブ調査では，驚くほど不真面目な回答が見られるものです。人間は基本的にラクをしたい生き物なので，一部の人は調査に回答する際に「なるべく認知的なリソースを使わずに回答してしまおう」と考えることがあり，これを努力の最小限化（satisficing: Krosnick, 1991）と呼びます。

調査を行う人達は，長い間この「努力の最小限化」に対抗するために様々な方法を考えてきました（e.g., Curran, 2016）。ここでは，明らかな適当回答を除外するためのいくつかの方法を紹介し，最後に実際に除外を行ってみます。

3.2.1 指示項目

質問紙を作る段階の話ですが，「この項目は一番右を選んでください」など，尺度の内容とは無関係に回答を指示する項目や，「私はここ1ヶ月寝ていない」など回答が絶対に一つに決まるはずの項目を入れておく，というのが最も簡便に利用可能な検出方法だと思います。ただ，1問だけの場合，たまたま適当に指示項目を通過してしまう可能性があるため，鬱陶しくならない程度に複数個入れておくと良いかもしれません。また，Web調査で項目をランダマイズする場合には，指示項目が一番上に来ないように，指示項目だけ表示順を固定するなど気をつけると良さそうです。

指示項目を使用した場合には，その項目についてsubset()を使えば良いので除外も簡単ですね。除外する際には，論文に記載するために何％もしくは何人がそこで脱落したかを数えておきましょう。 Rでカウントする際には，以下のような方法が考えられます。

コード 3.22: 特定の条件を満たさない人の数を数える

# 仮にQ1_1が指示項目で
# 「この項目では，右から2番め(5)を選んでください」
# と指示していたとしたら

# subsetによる方法
nrow(subset(dat, Q1_1 != 5))

[1] 2244

# もっとシンプルな方法
sum(dat[, "Q1_1"] != 5)

[1] 2244

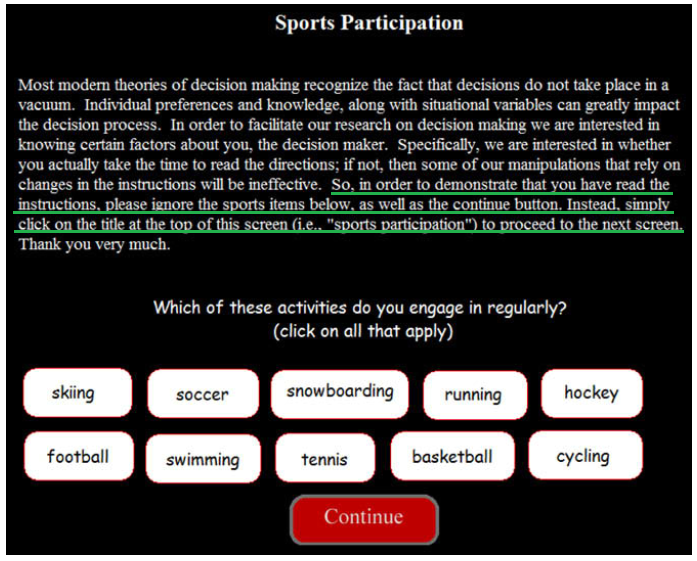
また，IMC （Instructional manipulation check, Oppenheimer et al., 2009）と呼ばれる方法も同じような効果を持ちます。この方法では，項目ではなく教示文に特別な指示を入れます。図 3.2 では，項目自体は「よくやる運動」を尋ねているのですが，IMCでは「タイトル（Sport Participation）をクリックしてね」という指示を与えています。その結果，元論文では46%もの人が引っかかってしまい，スポーツ名や下の”Continue”をクリックしてしまったそうです。 IMCは心理尺度の中に混ぜると言うよりは，例えば教示として状況や特定の物事に関する説明文をおく必要がある場合に使えそうな方法と言えます。長い説明文の最後か途中に「この内容を読んで正しく理解できた方は，この後の『正しく理解できた』の項目で『いいえ』を選択してください」や「次の段落の最初の文字をマルで囲んでください」のような指示を入れておく，といったやり方が考えられます。

ただ，IMCは場合によっては半数以上，多い時で8割以上も引っかかってしまうことがある（三浦・小林，2016）ので，最終的なサンプルサイズが小さくなりすぎないように気をつける必要があるかもしれません。裏を返せば，それだけウェブ調査はまともに回答されていない，ということなのかもしれませんが…。

3.2.2 回答時間

Web調査の場合，回答時間のデータも取得可能です⁶。回答時間を用いて適当回答を除外する場合，基本的には閾値を設けて，早すぎる・遅すぎる回答者を除外するという方法がとられます（e.g., Huang et al., 2012）。一般的に回答時間を用いる場合，一項目ごとの時間を収集することが望ましい (OIOS: One-item-one-screen)とされています。これは，例えば後半で疲れてしまいその後の回答が適当になってしまった場合を検出できるなど，回答行動内での動きをきめ細かくチェックできるようになるためです。

実際にどの程度の閾値を用いるかはケースバイケースです。単純に設問文が長い項目だったり，内容的に複雑な思考を必要とするような項目では所要時間は必然的に長くなるでしょう。一部の研究では，内容的に絶対にまともに回答することができないであろう時間（3秒など）を閾値とする考え方（Kong et al., 2007）なども提案されていますが，多くの先行研究ではデータから閾値を動的に決めています。 Höhne & Schlosser （2018）では，先行研究で用いられた閾値のいくつかを表 3.1 のようにまとめてくれています。

表 3.1: 回答時間の閾値（Höhne & Schlosser, 2018, Table 1）

下側の閾値	上限の閾値
平均値\(-2\times\mathrm{SD}\)	平均値\(+2\times\mathrm{SD}\)
中央値\(-1.5\times\)四分位範囲	中央値\(+1.5\times\)四分位範囲
中央値\(-1.5\times\)（中央値\(-\)第1四分位点）	中央値\(+1.5\times\)（第3四分位点\(-\)中央値
中央値\(-3\times\)（中央値\(-\)第1四分位点）	中央値\(+3\times\)（第3四分位点\(-\)中央値）
下側1%	上側1%

ということで，回答時間をもとに適当回答を検出するためには，分位点を計算できるようになっておくと良さそうです。 Rではお好きな分位点を以下のように求めることが出来ます。

コード 3.23: quantile(): 分位点を求める

# データに回答時間が無いので，今回はageの分位点を求めます
# 普通に実行すると，最大値・最小値と四分位数が出てくる
quantile(dat[, "age"])

  0%  25%  50%  75% 100% 
   3   20   25   35   86

# 引数probsに0から1の間の値を指定すると，対応する分位点が求められる
quantile(dat[, "age"], probs = c(0.01, 0.99))

   1%   99% 
12.00 59.65

実際にデータを除外する場合には，1項目でも基準に引っかかったらアウト，とはしないことが多いです。 複数の項目の回答時間（引っかかった項目数）に加えて，この後紹介するような方法によって実際の回答内容を見ながら総合的に判断していきます。

そして閾値の決め方に正解はありません。「疑わしきは罰せず」の姿勢でいった場合には適当回答の影響で回答の分布が歪むかもしれない一方で，「疑わしきは罰する」の姿勢の場合には一部の真面目な回答も除外してしまうために回答の分布が歪む可能性があります。余裕があれば，いろいろな閾値のもとで同じ分析を行って結果が変わらないことを確認（感度分析）すると良いでしょう。

3.2.3 回答内容の不一致

項目の組み合わせや回答方法次第では，回答内容の不一致によって疑わしい人を検出できるかもしれません。例えば今回使用しているデータにはageとeducationという項目があります。海外ならば飛び級制度があるので一概にルールを決めるのは難しいですが，日本であれば1年だけ「飛び入学」または「早期卒業」が可能なようです。ということは，「17歳未満の高卒以上」や「20歳未満の大卒」は日本のルール的には不可能なため，そのような回答をしている人は怪しいかもしれません。ただし，これは少なくとも年齢または学歴の項目について適当に回答または記入ミスがあるというだけであり，心理尺度の部分は正しく回答している可能性も十分にあります。そのため，上記のような「1つのミス」によって該当者の全ての回答を除外するかは要検討です。例えば，「学歴によって因子構造が変わるか」を検証したい場合であれば，学歴が正しく記入されていない可能性のあるデータは使用できないでしょう。というように，目的に応じて使うかどうかを決めるのが良さそうです。

他にも，成人のADHDを診断するための尺度であるCAARS （Conners’ Adult ADHD Rating Scales: Conners et al., 1999）には矛盾指標というものが用意されています。これは，例えば「1つの場所に長時間いることが難しい」と「じっと座っているときでも，内心は落ち着かない」のように，普通に考えたらだいたい同じ回答が得られそうな項目ペアについて差得点を出すことで，誠実に回答しているかを判断する方法です。特定の構成概念を測定するための一般的な心理尺度では，CAARSの矛盾指標のように確立された項目対が用意されているわけではないですが，通常全ての項目が同じような内容を尋ねているわけですから，同じような考え方で，あまりにも回答が不安定な人は怪しい，と判断できるかもしれません。

ということでここからは，不適切回答を検出するためのいくつかの手法を提供しているcarelessパッケージを用いたやり方を紹介していきます。

# install.packages("careless")
library(careless)

同じ構成概念を測定しようとしている心理尺度の場合，内容をきちんと読んで回答しているならば，基本的には各項目に対して同じような選択肢（例えば全て「あてはまる」寄り）を選ぶはずです。言い換えると，そのような場合には回答の個人内標準偏差が小さくなっていると考えられます。 …という考え方に基づいているのがIntra-individual Response Variability （IRV: Dunn et al., 2018）です。大層な名前がついていますが，やっていることは単純な標準偏差です。 carelessパッケージにはirv()という関数が用意されています。

コード 3.24: irv(): 尺度内標準偏差を求める

# 最初の5項目（Q1_1-Q1_5）は同じ特性を測定しているので，ばらつきは小さいはず
irv(dat[, paste0("Q1_", 1:5)])

        1         2         3         4         5         6         7 
0.8944272 1.5165751 0.5477226 0.8366600 1.1401754 0.5477226 1.4142136 
        8        10        11        13        14        15        16 
1.7888544 1.6431677 0.8366600 0.7071068 0.5477226 1.6431677 1.5165751 
       17        18        19        20        21        22        23 
1.6733201 0.4472136 0.7071068 0.8366600 1.6431677 2.5884358 2.0736441 
       24        25        26        27        28        29        30 
1.6431677 0.7071068 2.7386128 0.8944272 1.7320508 1.7888544 0.7071068 
       31        32 
2.1679483 1.7320508 
 [ reached getOption("max.print") -- omitted 2406 entries ]

irv()の基本的な挙動は，与えられたデータに対して行ごとに標準偏差を取っているだけなので，先程のコードを今までに登場した関数で表せばapply(dat[,paste0("Q1_",1:5)], 1, sd)と同じことです。一応irv()関数は他にも，引数次第で「前半のIRV」「後半のIRV」というようにデータを等分割してそれぞれのパートでのIRVを出してくれる機能もあります。調査で言えば，途中で疲れて後半が適当になっている人を検出したり，datの25項目のように複数の異なる特性に関する項目が並んでいる場合には役に立つかもしれません。

コード 3.25: 分割してから尺度内標準偏差を求める

# split = TRUEにしてnum.splitで分割数を決める
# ただし等分割しかしてくれない
irv(dat[, paste0("Q1_", 1:25)], split = TRUE, num.split = 5)

  irvTotal      irv1      irv2      irv3      irv4      irv5
1 0.900000 0.8944272 0.8366600 0.5477226 0.8366600 1.3038405
2 1.294862 1.5165751 0.7071068 2.1213203 1.0954451 0.8366600
3 1.092398 0.5477226 1.2247449 1.0954451 1.1401754 1.5165751
4 1.166190 0.8366600 0.8366600 0.7071068 1.6431677 0.8944272
5 1.000000 1.1401754 1.1401754 1.5165751 0.8366600 0.4472136
6 1.863688 0.5477226 2.3021729 2.3452079 1.2247449 1.9235384
7 1.607275 1.4142136 1.1401754 0.8366600 0.5477226 2.1679483
8 1.519868 1.7888544 1.0000000 1.9235384 1.7888544 1.1401754
 [ reached 'max' / getOption("max.print") -- omitted 2428 rows ]

3.2.4 ストレートライン

上で説明したように，心理尺度では，内容をきちんと読んで回答しているならば，基本的には同じ選択肢を選ぶはずです。とはいえ，完全に同じ選択肢を選び続けると言うよりは，細かい内容の違い等によって，少しずつ異なる回答をすることが期待されています⁷。リッカート尺度は表形式で尋ねることが多く，そのようなフォーマットに対する努力の最小限化は，縦一列に同じ選択肢を選び続けるという形で表れると考えられます。特に逆転項目（「～ではない。」のような項目）があるにも関わらずそれを無視して同じ選択肢を選び続けている場合は要注意です。

このように「ずっと同じ選択肢を選び続けている」状態をストレートラインやlong stringなどと呼びます。一般的には，ずっと同じ選択肢を選び続けた最大の長さ (long string index) を計算して，これが閾値より大きい人は要注意，という感じで利用します。 long string indexをRで計算するのは結構骨が折れる作業なのですが，carelessパッケージにはlongstring()という関数が用意されています。ありがたい。

コード 3.26: longstring(): 最長の同一回答数を計算する

# ストレートラインは内容の違いに関わらず続くはず
# ということで，25項目全部あたえてやる
longstring(dat[, paste0("Q1_", 1:25)])

  [1] 3 4 3 3 3 3 2 1 5 2 4 3 3 3 5 4 3 3 2 2 6 3 3 4 3 3 2 4 3 3 3 3
 [33] 3 5 2 7 2 3 4 3 4 4 2 2 4 4 3 4 3 3 5 4 4 4 7 3 2 2 2 4 3 3 3 3
 [65] 3 3 3 3 2 4 3 3 4 3 2 2 3 3 3 4 3 3 5 3 3 3 2 3 4 3 3 3 2 3 3 2
 [97] 2 3 3 3
 [ reached getOption("max.print") -- omitted 2336 entries ]

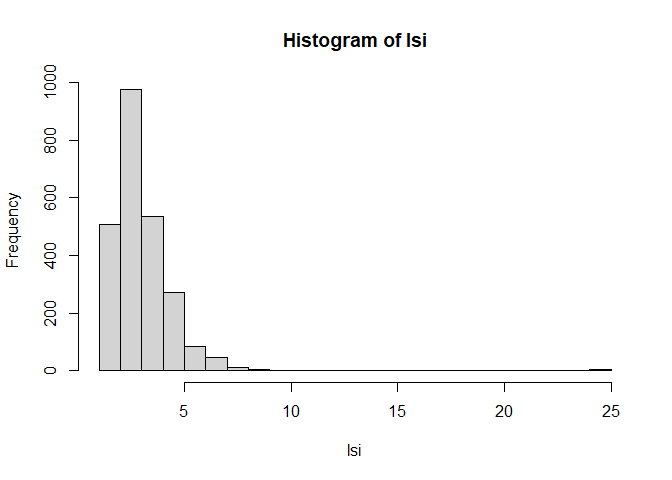
実際にIRVやlong string indexを除外基準として利用する場合の閾値は，やはりケースバイケースです。一つの方法としては，ヒストグラムを作成して視覚的に決めるのが良いでしょう。

コード 3.27: long string indexのヒストグラムを見る

lsi <- longstring(dat[, paste0("Q1_", 1:25)])
# hist()関数でヒストグラムを作れる
hist(lsi)

図 3.3 を見ると，大体7か8くらいより大きい人は怪しそうな気がします。ヒストグラムの他にも，quantile()関数を使って上位何%の人が怪しい，といった検出方法も考えられますが，いずれにしてもlong string index（やirv）の値だけで機械的に除外するのではなく，可能な限り回答の内容も踏まえて除外するかを決めるようにしましょう。

ちなみに，今回のデータでは項目の出題順は個人ごとにランダムであったと思われます。 このような場合，ストレートラインによる除外は意味を成さないので気をつけてください⁸。また，ストレートラインと似た適当回答としては，複数個でパターンを繰り返すもの(e.g., 123451234512345…)や，階段状に回答するもの(e.g., 2345432345432…)などもあります。本当はこれらも全部検出してあげるのがベストなのですが，残念ながらlongstring()関数では対応できないので，自分で関数を作成する必要があります。これはめちゃめちゃ面倒なので今回は省略します⁹。

longstring()関数を使わずにストレートラインを計算する

以下では，longstring()関数を使わずに最長ストレートラインを計算するコードの実装例を紹介します。一応各ステップでの状態も載せておくので，各行で何が行われているか確かめながら読み進めてください。また，やり方は他にも色々あるので，もしよければ自分で考えて実装してみてください。

# 以下のデータ（3人目のQ1_1からQ1_25）について計算してみる
vec <- dat[3, 2:26] # 面倒なので列番号で指定してしまいます
vec

  Q1_1 Q1_2 Q1_3 Q1_4 Q1_5 Q1_6 Q1_7 Q1_8 Q1_9 Q1_10 Q1_11
3    5    4    5    4    4    4    5    4    2     5     2
  Q1_12 Q1_13 Q1_14 Q1_15 Q1_16 Q1_17 Q1_18 Q1_19 Q1_20
3     4     4     4     5     4     5     4     2     3
  Q1_21 Q1_22 Q1_23 Q1_24 Q1_25
3     4     2     5     5     2

is_same <- vec[, 2:25] == vec[, 1:24] # 前の項目と同じならTRUE
is_same # 一旦表示してみる

   Q1_2  Q1_3  Q1_4 Q1_5 Q1_6  Q1_7  Q1_8  Q1_9 Q1_10 Q1_11
3 FALSE FALSE FALSE TRUE TRUE FALSE FALSE FALSE FALSE FALSE
  Q1_12 Q1_13 Q1_14 Q1_15 Q1_16 Q1_17 Q1_18 Q1_19 Q1_20
3 FALSE  TRUE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE
  Q1_21 Q1_22 Q1_23 Q1_24 Q1_25
3 FALSE FALSE FALSE  TRUE FALSE

is_same <- as.numeric(is_same) # 数字に変換
is_same # 一旦表示してみる

 [1] 0 0 0 1 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 1 0

is_same <- paste(is_same, collapse = "") # 全部くっつける
is_same # 一旦表示してみる

[1] "000110000001100000000010"

# 連続する1の最長を数えて1を足せば良いので
straight_line <- strsplit(is_same, split = "0") # 文字列を0の位置で切断
straight_line # 一旦表示してみる

[[1]]
 [1] ""   ""   ""   "11" ""   ""   ""   ""   ""   "11" ""  
[12] ""   ""   ""   ""   ""   ""   ""   "1"

# 文字数に変換
# strsplit()はリストを返すため，リストの1番目を選択
# リストについてはそのうち説明します
straight_line <- nchar(straight_line[[1]])
straight_line # 一旦表示してみる

 [1] 0 0 0 2 0 0 0 0 0 2 0 0 0 0 0 0 0 0 1

# 最大値に1を足せば最長が分かる
max(straight_line) + 1

[1] 3

これでようやく1人分の最長ストレートラインが計算できました。本当はこれを（apply()などを使って）全員に対して計算した上で，一定数より大きい人を除外するか検討する，といった手続きを取る必要があるわけです。

3.2.5 人と違う回答

心理尺度の場合，同じ構成概念を尋ねている各項目はそれなりに相関しているはずです。もちろん項目によってそもそも当てはまりにくい・当てはまりやすい項目はあるのですが，総合すると項目への回答には「平均的なパターン」と言えるものがありそうです。「人と違う」を検出する方法は，異常検知の知見が使えたりします。したがって機械学習を利用して検出する方法なども研究されていたりしますが，ここでは伝統的なマハラノビス距離を用いた検出方法を紹介＆実践してみたいと思います。

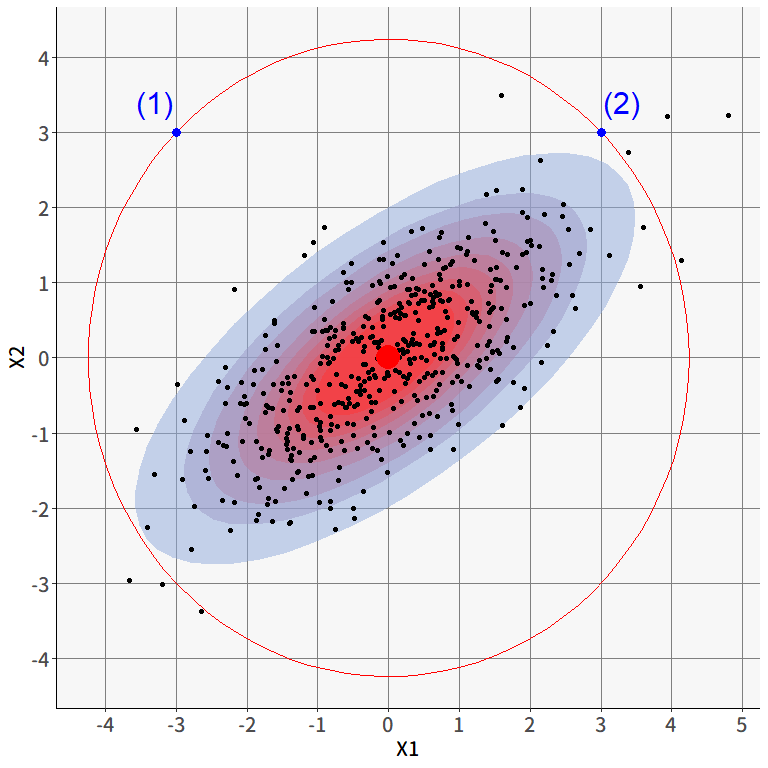
図 3.4 は，２項目の連続的な項目（６段階評価ではなく，スライダーみたいなもので回答したと想像してください）への回答をプロットした仮想的なものです。赤い点がそれぞれの軸の平均値を表しています。青い点(1)と(2)は，それぞれ赤い点からの直線距離はほぼ同じなのですが，2変数の相関を考えると(2)の方はさほどおかしな値ではなさそうです。正の相関があるため，平均値から離れていたとしても2項目とも一貫して高い or 低い値ならばありえる，ということですね。

このような時に使えるのがマハラノビス距離です。変数の相関関係を考慮した上でベクトル間の距離を出してくれます。回答者\(i\)の回答ベクトルを\(\symbf{x}_i\)，全回答者の平均ベクトルを\(\bar{\symbf{x}}\)，変数の分散共分散行列を\(\symbf{\Sigma}_{\symbf{x}}\)とすると，マハラノビス距離は \[ \begin{aligned} D=\sqrt{(\symbf{x}_i-\bar{\symbf{x}})\symbf{\Sigma}_{\symbf{x}}^{-1}(\symbf{x}_i-\bar{\symbf{x}})^{\top}} \end{aligned} \tag{3.1}\] で計算することが出来ます。マハラノビス距離は，多変量正規分布と密接な関係を持っています。というのも，\(k\)個の変数に関する多変量正規分布の確率密度関数は \[ \begin{aligned} f(\symbf{x};\symbf{\mu},\symbf{\Sigma})=\frac{1}{\sqrt{(2\pi)^k |\symbf{\Sigma}|}}\exp\left(-\frac{1}{2}(\symbf{x}_i-\symbf{\mu})\symbf{\Sigma}_{\symbf{x}}^{-1}(\symbf{x}_i-\symbf{\mu})^{\top}\right) \end{aligned} \tag{3.2}\] と表されますが，よく見るとこの式の中には(3.1)式のルートの中身によく似たものが入っています。実際に，データから多変量正規分布の平均ベクトル\(\symbf{\mu}\)と分散共分散行列\(\symbf{\Sigma}\)を最尤推定する場合，最尤推定量はそれぞれ標本平均ベクトル\(\bar{\symbf{x}}\)と標本共分散行列\(\symbf{\Sigma}_{\symbf{x}}\)となることが知られています。したがって，マハラノビス距離はデータから推定された多変量正規分布の確率密度に反比例するということがわかります。言ってしまえば，マハラノビス距離は個人レベルでみたときの尤度みたいなもの，というわけですね。図 3.4 で言えば，塗りつぶされている楕円が，データから推定されたニ変量正規分布における大まかな確率密度を表していますが，マハラノビス距離はこの確率密度に応じて計算されているわけです。そう考えると，確かに(2)の点のほうが(1)の点よりも中心からの距離は短い，と判断できそうです。

Rにはマハラノビス距離（の二乗）を計算するための関数mahalanobis()が用意されているため，これを使って図 3.4 の2つの青い点のマハラノビス距離を計算してみます。mahalanobis()では，基本的に3つの引数をとります。第一引数xには\(\mathbf{x}_i\)を，第二引数center¹⁰には\(\bar{\mathbf{x}}\)を，第三引数covには\(\symbf{\Sigma}_{\symbf{x}}\)に相当するものを入れてあげましょう。

コード 3.28: マハラノビス距離の計算

# ここのコードは見ているだけでOKです。
mean_vec <- c(0, 0) # 平均ベクトル
cov_matrix <- matrix(c(1, 0.9, 0.9, 1), nrow = 2) # 分散共分散行列
# 各変数の分散が１，相関係数が0.9という想定です。
cov_matrix # 一応表示してみる

     [,1] [,2]
[1,]  1.0  0.9
[2,]  0.9  1.0

vec1 <- c(-3, 3) # 青い点(1)の座標
# 青い点(1)のマハラノビス距離
mahalanobis(vec1, center = mean_vec, cov = cov_matrix)

[1] 180

vec2 <- c(3, 3) # 青い点(2)の座標
# 青い点(2)のマハラノビス距離
mahalanobis(vec2, center = mean_vec, cov = cov_matrix)

[1] 9.473684

ということで，青い点(1)，(2)と平均ベクトルとのマハラノビス距離（の二乗）はそれぞれ180，9.47となり，たしかに(1)のほうが大きな外れ値であるということがわかりました。

ありがたいことにcareless()パッケージには，データフレームからマハラノビス距離を計算するための関数も用意されています。先程使用したmahalanobis()関数では，自分でデータから平均ベクトルと分散共分散行列を計算する必要があったのですが，carelessパッケージにあるmahad()関数ではデータフレームを一つ与えるだけで各行のマハラノビス距離をまとめて計算してくれます¹¹。ありがたい。

コード 3.29: mahad(): データフレームの各行のマハラノビス距離を計算する

mahad(dat[, paste0("Q1_", 1:25)])

 [1] 13.468425 25.677291 13.490783 28.823203 18.946470 25.901522
 [7]  9.260945 48.474541 12.794634 19.207672 19.386422 14.485101
[13] 34.052697 38.710674 18.843160 18.056494 26.822273 38.451815
[19] 47.752717 30.685610 24.097729 27.202401 10.453943 30.186948
[25] 20.393634 12.667231 45.024926 23.116322 26.807564 12.173940
[31] 56.951093 20.122730 26.353218 30.358047 17.898820 28.093556
[37] 14.465344 10.483335 11.724812 27.950268  7.693067 57.603758
[43] 23.731495 20.956441 42.950337 14.636132 32.755405 52.321123
 [ reached getOption("max.print") -- omitted 2388 entries ]

これで無事，全員分のマハラノビス距離を一気に計算できました。あとはこれを利用して怪しい人を検出するだけです。ですがこの場合でも閾値の問題が登場します。これまで通り，ヒストグラムを描いてみたり，quantile()を利用してみても良いのですが，mahad()関数にはもう少しテクニカルな方法が実装されています。

\(p\)次元多変量正規分布に従うデータから計算されるマハラノビス距離の二乗は，理論的には自由度\(p\)の\(\chi^2\)分布に従うことが知られています。これを利用すると，「自由度\(p\)の\(\chi^2\)分布における上位\(k\)パーセンタイル点より大きい人を検出しよう」という考えに至ります。

コード 3.30: マハラノビス距離に基づく検出

# flag = TRUEにすると，フラグを立ててくれる
# confidenceによって，閾値のパーセンタイル点を決める
m_dist <- mahad(dat[, paste0("Q1_", 1:25)], flag = TRUE, confidence = 0.99)
m_dist

        d_sq flagged
1  13.468425   FALSE
2  25.677291   FALSE
3  13.490783   FALSE
4  28.823203   FALSE
5  18.946470   FALSE
6  25.901522   FALSE
7   9.260945   FALSE
8  48.474541    TRUE
9  12.794634   FALSE
10 19.207672   FALSE
11 19.386422   FALSE
12 14.485101   FALSE
13 34.052697   FALSE
14 38.710674   FALSE
15 18.843160   FALSE
16 18.056494   FALSE
17 26.822273   FALSE
18 38.451815   FALSE
19 47.752717    TRUE
20 30.685610   FALSE
 [ reached 'max' / getOption("max.print") -- omitted 2416 rows ]

ここでflagged列がTRUEになっている人が，マハラノビス距離が閾値より大きい，すなわち異質な回答パターンを示した人だということです。

ちなみに，マハラノビス距離が最大の人の回答ベクトルを見てみると，たしかにこの人は６か１かばかりで回答しており，どうやら適当に回答しているような気がします。ただ実際には日頃から極端な選択肢を選ぶ傾向がある人かもしれないので，これだけで機械的に除外するのではなく，回答ベクトルを見てストレートラインの傾向が無いかなども確認して除外の判断をしたほうが良いでしょう。

コード 3.31: マハラノビス距離が最大の人の回答を見てみる

# which.max()はベクトルの中で最大値の「位置」を返す (arg max 的な)
# max()は最大値そのものを返す
# which.min()もあるよ
dat[which.max(m_dist$d_sq), ]

     ID Q1_1 Q1_2 Q1_3 Q1_4 Q1_5 Q1_6 Q1_7 Q1_8 Q1_9 Q1_10 Q1_11
867 867    6    6    6    6    6    6    5    1    1     1     6
    Q1_12 Q1_13 Q1_14 Q1_15 Q1_16 Q1_17 Q1_18 Q1_19 Q1_20 Q1_21 Q1_22
867     6     1     6     6     1     6     1     6     1     6     6
    Q1_23 Q1_24 Q1_25 gender education age
867     1     6     1      1         1  31

マハラノビス距離による検出法の弱点

マハラノビス距離は平均ベクトルからの距離を求めています。そのため，同じストレートラインでも1と6ばかりなど極端な選択肢を選んでいる人は引っかかりやすい一方で，3と4（どちらでもない周辺）ばかりを選んでいる人はどうしてもマハラノビス距離は小さくなってしまいます。同様に，どちらでもない周辺で適当な回答をしている人は検出しにくいという問題点があります。

これを克服するためには，マハラノビス距離に加えてIRVやストレートラインなどの指標，あるいは可能であれば回答データ以外（回答時間など）の複数の指標を組み合わせて検出してあげるのが良さそうです。

また，そもそもマハラノビス距離は，多変量正規分布の確率密度に比例する値であるという点にも注意が必要です。天井・床効果程度なら多分問題ないのですが，例えば6件法で1と6（極端な選択肢）に回答が集中するような場合には，回答の分布が二峰になっているので，そもそも正規分布を当てはめることが怪しくなってきます。そのような場合にはマハラノビス距離を使うこと自体もよく考えたほうが良さそうです。

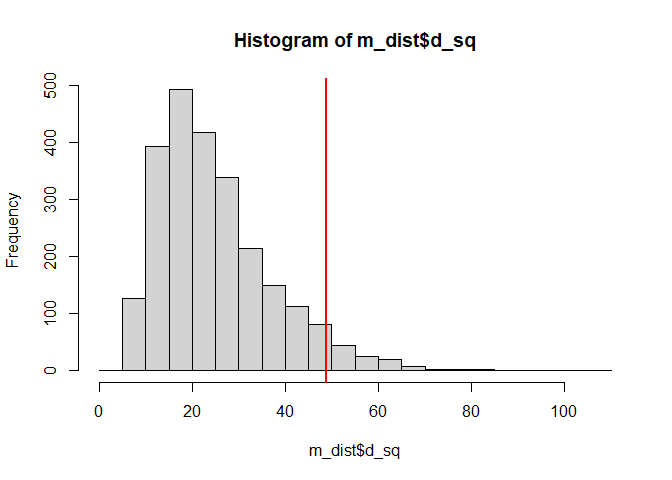
ここまで適当回答を検出するためのいくつかの方法を紹介してきました。実際のデータにおいて検出＆除外を行うときにはいろいろと考えるべきことはあるのですが，とりあえず今回は機械的に「long string index (lsi)が8以上」かつ「マハラノビス距離が上位5%¹²」の人を除外することにします。ちなみにマハラノビス距離の上位5%は，図 3.5 の分布でいえば赤い線より右側の人であり，極端に大きい人たちだろうということが言えそうです。

では，実際に2つの基準をともに満たす人を除外してみましょう。ここでは，複数の条件式を結合するための論理演算子を使用します。論理演算とは，複数のTRUE/FALSEをもとに1つのTRUE/FALSEを返す演算のことです。何はともあれ，以下の例を見てください。

コード 3.32: &演算子: 2つともTRUEのときだけTRUEを返す (AND)

TRUE & TRUE
TRUE & FALSE
FALSE & FALSE

[1] TRUE
[1] FALSE
[1] FALSE

コード 3.33: |演算子: いずれか一つでもTRUEであればTRUEを返す (OR)

TRUE | TRUE
TRUE | FALSE
FALSE | FALSE

[1] TRUE
[1] TRUE
[1] FALSE

今回は，AND演算子 (&)を用いて「long string index (lsi)が8以上」かつ「マハラノビス距離が上位5%」の人を探し出したいと思います。

コード 3.34: 複数条件を満たす人を見つける(1)

# まずはマハラノビス距離の閾値を求める
thres <- quantile(m_dist$d_sq, prob = 0.95)
thres

     95% 
48.87949

コード 3.35: 複数条件を満たす人を見つける(2)

# 除外対象となる人を判別する
is_remove <- (m_dist$d_sq >= thres) & (lsi >= 8)
is_remove

 [1] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[12] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[23] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[34] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[45] FALSE FALSE FALSE FALSE FALSE FALSE
 [ reached getOption("max.print") -- omitted 2386 entries ]

# 何行目の人が除外されるかを一応チェック
which(is_remove)

[1] 1243 1359 1775 2018

# 一応除外対象の人の回答をチェック
subset(dat, is_remove)

       ID Q1_1 Q1_2 Q1_3 Q1_4 Q1_5 Q1_6 Q1_7 Q1_8 Q1_9 Q1_10 Q1_11
1430 1430    1    1    1    1    1    1    1    1    1     1     1
1560 1560    1    6    6    1    1    5    6    6    4     6     1
2043 2043    1    1    1    1    1    1    1    1    1     1     1
2313 2313    6    1    1    6    1    6    5    6    1     1     6
     Q1_12 Q1_13 Q1_14 Q1_15 Q1_16 Q1_17 Q1_18 Q1_19 Q1_20 Q1_21
1430     1     1     1     1     1     1     1     1     1     1
1560     6     6     1     6     6     6     6     6     6     6
2043     1     1     1     1     1     1     1     1     1     1
2313     6     1     1     1     1     1     1     1     1     6
     Q1_22 Q1_23 Q1_24 Q1_25 gender education age
1430     1     1     1     1      1         3  23
1560     6     4     6     1      2         5  31
2043     1     1     1     1      1         3  19
2313     1     1     6     1      1         3  23

コード 3.36: 複数条件を満たす人を見つける(3)

# is_removeがFALSEの人だけ残せば良いので
dat <- subset(dat, !is_remove)

ということで，残ったデータは

nrow(dat)

[1] 2432

となりました。以後の分析はこの2432人分のデータで進めていきます。

AND/OR演算子とNA

以前，論理演算子（==や>など）にNAを与えた場合には，「判断不可能」的な意味合いのNAが返ってきてしまう，という話がありました。では，AND/OR演算子にNAが与えられた場合どうなるかというと，これはやや複雑な挙動となります。一言で言えば，NAにTRUEとFALSEのどちらが入るのかによって結果が変わる場合には「判断不可能」のNAが返ってきます。 あとは下の例を見て理解してください。

TRUE & NA
FALSE & NA
TRUE | NA
FALSE | NA

[1] NA
[1] FALSE
[1] TRUE
[1] NA

3.3 逆転項目の処理

心理尺度では，内容を読まずに「慣れ」でストレートライン的回答を避けたい，といった目的から意図的に「＊＊ではない」のように否定語を使ったり，構成概念をきちんと反映した項目として，意味的に反対のことを尋ねる（例えば，社交性を測定する尺度において「休日は基本的に家から出ない」のような項目を入れておく）ことがあります。こうした項目は逆転項目と呼ばれ，分析の際には，多くのケースにおいて事前に得点をひっくり返す必要があります。 psych::bfiでは¹³1, 9, 10, 11, 12, 22, 25番目の項目が逆転項目となっています。

逆転項目の処理自体は何も難しいことはなく，リッカート尺度の場合は「（最大値+最小値）から回答の値を引く」だけでOKです。ということで，一つの列について逆転項目の処理を行うならば以下のコードで可能となります。

コード 3.37: 逆転項目の処理（1項目編）

dat[, "Q1_1"] # 処理前

  [1] 2 2 5 4 2 6 2 4 2 4 5 5 4 4 4 5 4 4 5 1 1 2 4 1 2 2 2 4 1 2 1 2
 [33] 5 1 1 1 1 1 1 5 2 1 5 2 1 1 1 1 3 4 1 1 1 3 1 3 2 2 4 2 1 4 2 1
 [65] 4 4 1 3 2 2 5 1 2 1 1 1 1 1 4 1 1 1 1 1 2 1 2 2 3 1 4 2 3 2 1 1
 [97] 1 6 2 3
 [ reached getOption("max.print") -- omitted 2332 entries ]

dat[, "Q1_1"] <- 7 - dat[, "Q1_1"]
dat[, "Q1_1"] # 処理後

  [1] 5 5 2 3 5 1 5 3 5 3 2 2 3 3 3 2 3 3 2 6 6 5 3 6 5 5 5 3 6 5 6 5
 [33] 2 6 6 6 6 6 6 2 5 6 2 5 6 6 6 6 4 3 6 6 6 4 6 4 5 5 3 5 6 3 5 6
 [65] 3 3 6 4 5 5 2 6 5 6 6 6 6 6 3 6 6 6 6 6 5 6 5 5 4 6 3 5 4 5 6 6
 [97] 6 1 5 4
 [ reached getOption("max.print") -- omitted 2332 entries ]

今回は7項目だけなので一つ一つやっても良いのですが，もっと項目数が多いと大変なのでapply()の力を借りましょう。今回の場合，apply()関数の引数Xには「datのうち逆転項目を処理したい列だけ」，MARGINは2，FUNには「7から引く」という関数を指定してあげたら良いわけです。ですが困ったことにRには「7から引く」なんていうspecificな関数は存在していません。こういう時には，関数を定義するという方法を使う必要があります。簡単な関数を定義している例を挙げてみましょう。

コード 3.38: 関数を作ってみる

# function()関数は「関数を定義する」関数
# ()の中には新しく作る関数の引数を
# {}の中には関数の動作を記入する
tashizan <- function(x, y) {
  x + y
}
tashizan(3, 2)

[1] 5

この関数tashizan()はもちろんRにもともと存在しない，与えられた２つの引数xとyの和を返す関数です¹⁴。同じ要領で，「7から与えられた値を引く」という関数を作りましょう。

コード 3.39: 「7から引く」関数を作ってみる

subtract_7 <- function(x) {
  7 - x
}
# 挙動の確認
head(dat$Q1_9) # 処理前

[1] 4 3 2 5 3 1

subtract_7(head(dat$Q1_9)) # 関数を適用

[1] 3 4 5 2 4 6

これをapply()関数の引数FUNに指定してあげれば，すべての列に同じ処理を適用することができるわけです。

コード 3.40: 逆転項目の処理（複数項目編）

# 処理する列名を指定
# 上のコードでQ1_1だけ逆転処理済みなのでここでは除外
cols <- paste0("Q1_", c(9, 10, 11, 12, 22, 25))
# cols <- c("Q1_9", "Q1_10", "Q1_11","Q1_12","Q1_22","Q1_25")
# ↑これでもよいが，列数が増えた時には大変

head(dat[, cols]) # 処理前

  Q1_9 Q1_10 Q1_11 Q1_12 Q1_22 Q1_25
1    4     4     3     3     6     3
2    3     4     1     1     2     3
3    2     5     2     4     2     2
4    5     5     5     3     3     5
5    3     2     2     2     3     3
6    1     3     2     1     3     1

dat[, cols] <- apply(dat[, cols], 2, subtract_7)
head(dat[, cols]) # 処理後

  Q1_9 Q1_10 Q1_11 Q1_12 Q1_22 Q1_25
1    3     3     4     4     1     4
2    4     3     6     6     5     4
3    5     2     5     3     5     5
4    2     2     2     4     4     2
5    4     5     5     5     4     4
6    6     4     5     6     4     6

これで，ようやく全ての逆転項目の処理が完了しました¹⁵。次章では，データの性質を確認して，収集したデータが「本当に使えるものなのか」を見ていきます。

コード 3.41: 最後に保存

saveRDS(dat, "chapter03.rds")

Conners, C. K., Erhardt, D., & Sparrow, E. P. (1999). Conners’ adult ADHD rating scales (CAARS): technical manual. Multi-Health Systems North Tonawanda, NY.

Curran, P. G. (2016). Methods for the detection of carelessly invalid responses in survey data. Journal of Experimental Social Psychology, 66, 4–19. https://doi.org/10.1016/j.jesp.2015.07.006

Dunn, A. M., Heggestad, E. D., Shanock, L. R., & Theilgard, N. (2018). Intra-individual response variability as an indicator of insufficient effort responding: comparison to other indicators and relationships with individual differences. Journal of Business and Psychology, 33(1), 105–121. https://doi.org/10.1007/s10869-016-9479-0

Höhne, J. K., & Schlosser, S. (2018). Investigating the adequacy of response time outlier definitions in computer-based web surveys using paradata SurveyFocus. Social Science Computer Review, 36(3), 369–378. https://doi.org/10.1177/0894439317710450

Huang, J. L., Curran, P. G., Keeney, J., Poposki, E. M., & DeShon, R. P. (2012). Detecting and deterring insufficient effort responding to surveys. Journal of Business and Psychology, 27(1), 99–114. https://doi.org/10.1007/s10869-011-9231-8

Kong, X. J., Wise, S. L., & Bhola, D. S. (2007). Setting the response time threshold parameter to differentiate solution behavior from rapid-guessing behavior. Educational and Psychological Measurement, 67(4), 606–619. https://doi.org/10.1177/0013164406294779

Krosnick, J. A. (1991). Response strategies for coping with the cognitive demands of attitude measures in surveys. Applied Cognitive Psychology, 5(3), 213–236. https://doi.org/10.1002/acp.2350050305

Little, R. J. A. (1988). A test of missing completely at random for multivariate data with missing values. Journal of the American Statistical Association, 83(404), 1198–1202. https://doi.org/10.1080/01621459.1988.10478722

三浦麻子・小林哲郎（2016）．オンライン調査における努力の最小限化（Satisfice）傾向の比較 : IMC違反率を指標として　メディア・情報・コミュニケーション研究，1, 27–42.

Oppenheimer, D. M., Meyvis, T., & Davidenko, N. (2009). Instructional manipulation checks: Detecting satisficing to increase statistical power. Journal of Experimental Social Psychology, 45(4), 867–872. https://doi.org/10.1016/j.jesp.2009.03.009

Schafer, J. L., & Graham, J. W. (2002). Missing data: Our view of the state of the art. Psychological Methods, 7(2), 147–177. https://doi.org/10.1037/1082-989X.7.2.147

高橋将宜・渡辺美智子（2017）．欠測データ処理: Rによる単一代入法と多重代入法　共立出版

欠測データの処理についての日本語の書籍としては，例えば高橋・渡辺（2017）にはRのコードも掲載されているので，興味があれば見てみると良いかもしれません。↩︎
MCARの場合には，最悪欠測値がある人をリストワイズ削除しても問題ありません（サンプルサイズが小さくなるだけでバイアスにはならない）。MARの場合には，多重代入法(MI)や完全情報最尤推定法(FIML)を用いると，うまいこと欠測値を補完することができるとされています。↩︎
一応MCARかどうかを判別するための統計的検定法としてLittle’s MCAR test （Little, 1988）というものがあるようです。RにはBaylorEdPsych::LittleMCAR()という関数が作られているようです。使ったことはありません。↩︎
Rでは，「あるはずなのに無い（欠測）」はNA (Not Available)，「数字ではないもの(e.g., 0で割ったもの)」はNaN (Not A Number)，「もともと何もない」はNULL，無限大はInfという特殊な非数値が用意されており，それぞれis.***()関数で判定可能です。↩︎
カッコがたくさんあると読みにくくなってしまいます。だからといって，途中のオブジェクトをいちいち変数に代入する場合，変数の名前を（ムダに）考える必要が出てきてしまいます。こういった問題をクリアするのがパイプです。Rネイティブでも最近ようやく実装されました。例えばhead(dat)はdat |> head()という書き方が出来ます。パイプを使えば，処理の順番がわかりやすくなるかもしれません。↩︎
最も手軽にWeb調査フォームを作成する場合はGoogle Formが選択肢に上がるかと思いますが，どうやらGoogle Formには回答時間を記録する方法はなさそうです…同じWeb調査作成プラットフォームの中では，Questantやqualtricsでは，項目ごとではなく回答全体での所要時間の記録が可能なようです（項目単位で記録できるかは不明）。あるいはjavascriptが使えるならば jsPsych といったフレームワークもあります。こちらは心理学系の実験が色々出来ますが，その一環として普通のアンケートも実装可能であり，javascriptによって記録できる行動は（画面遷移やマウスカーソルの座標なども）理論上全て取得可能です。↩︎
本当に全ての項目に同じ回答を期待しているのであれば，複数項目用意する必要が無いですからね。複数項目用意しているのは，１項目では構成概念を十分に測定しきれないためです。↩︎
ランダムに出題されていた場合には，左から実際の出題順に回答を並べたデータを用意できれば同様にストレートラインの計算が可能です。↩︎
気になる人は個人的に教えます。ただ相当大変なので覚悟してください。↩︎
ふつうマハラノビス距離は「2つのベクトルの距離」なので2つの引数はxとyのほうがしっくり来るのですが，この関数の第二引数がcenterなのは，この関数が「データフレームの各行について，平均ベクトルからのマハラノビス距離を計算する」という，まさにいま行っている分析の目的にピッタリの関数だからです。↩︎
内部の計算はpsych::outlier()関数を使っています。なのでこちらを使用してもOKです。↩︎
勘違いしないでいただきたいのですが，「マハラノビス距離の上位5%を除外するのが定番」ということではありません。例えば最初から「上位5％の人にフラグを立てよう」と決め打ちにしていると，もし100人中50人が適当回答者だったとしても，そのうち5人しか検出できないことになります。なので今回の基準はあくまでも授業の演習としてとりあえず除外を体験してみよう，というくらいの意味合いです。↩︎
psych::bfi.keysで確認可能です。変数名の頭にマイナスがついているものが逆転項目です。↩︎
もちろん様々なパッケージにある関数も全て，どこかの誰かが必要にかられてfunction()によって定義してくれたものなのです。↩︎
実を言うと，apply()なんか使わなくても7 - dat[,cols]で複数行まとめて処理は可能です。今回は自作関数の導入を兼ねてちょっと回りくどいやり方にしました。↩︎