6 因子分析

abstract

複数の項目への回答に影響する共通の要因を抽出する分析法である（探索的）因子分析について，前半では理論的な考え方とRでのやり方を説明し，後半では実践上のいくつかのトピック（事前分析・回転・因子数の決定など）を解説しています。

本資料は，神戸大学経営学研究科で2022年度より担当している「統計的方法論特殊研究（多変量解析）」の講義資料です。CC BY-NC 4.0ライセンスの下に提供されています。

おまたせしました。ここからいよいよ本編中の本編です。まずは因子分析(factor analysis)です。はじめに因子分析の基本的＆数理的な考え方を紹介した後で，Rでやってみます。その後，因子分析を実施する上でのプラクティカルなポイントを押さえていきます。

コード 6.1: 事前準備

# パッケージのインストール
# ↓Chapter 1 でインストールしている人はスキップ
# install.packages("psych")
# ↓明示的には使わないのですが，psych::fa()で必要になるので
# install.packages("GPArotation")

# データの読み込み
dat <- readRDS("chapter04.rds")

6.1 因子分析とは

今回使用しているdatのQ1_11からQ1_15はいずれも外向性(extraversion)を測定している項目です。実際に項目を見てみると¹

Don’t talk a lot. （【逆転】あまり喋らない。）
Find it difficult to approach others. （【逆転】人に近づきづらいと思う。）
Know how to captivate people. （人を魅了できる。）
Make friends easily. （友達を作りやすい。）
Take charge. （リーダータイプである。）

となっており，たしかに他人との関わりに関する内容を尋ねているようです。改めて項目間の相関を確認してみると，逆転項目も処理済みなので全ての項目間に正の相関があります。この相関構造を一つの指標にまとめたものの一つが $\alpha$ 係数でした。

コード 6.2: 項目間相関

# round()関数を使って表示桁数を減らしています
round(cor(dat[, paste0("Q1_", 11:15)]), 2)

      Q1_11 Q1_12 Q1_13 Q1_14 Q1_15
Q1_11  1.00  0.47  0.32  0.42  0.31
Q1_12  0.47  1.00  0.39  0.53  0.39
Q1_13  0.32  0.39  1.00  0.42  0.39
Q1_14  0.42  0.53  0.42  1.00  0.32
Q1_15  0.31  0.39  0.39  0.32  1.00

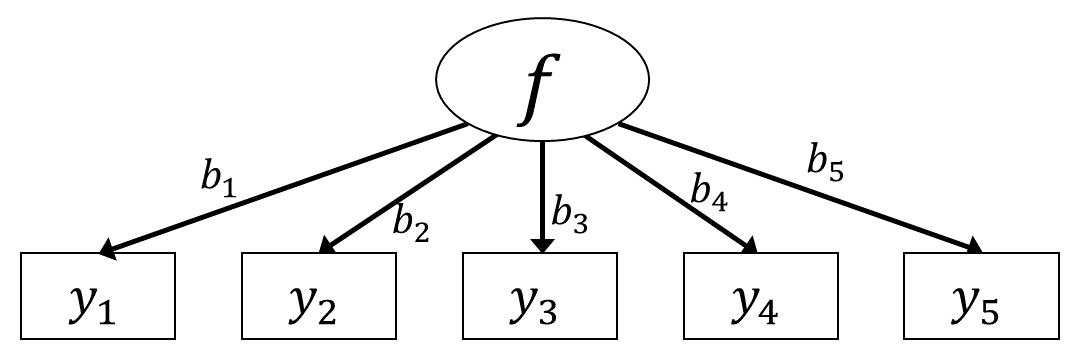
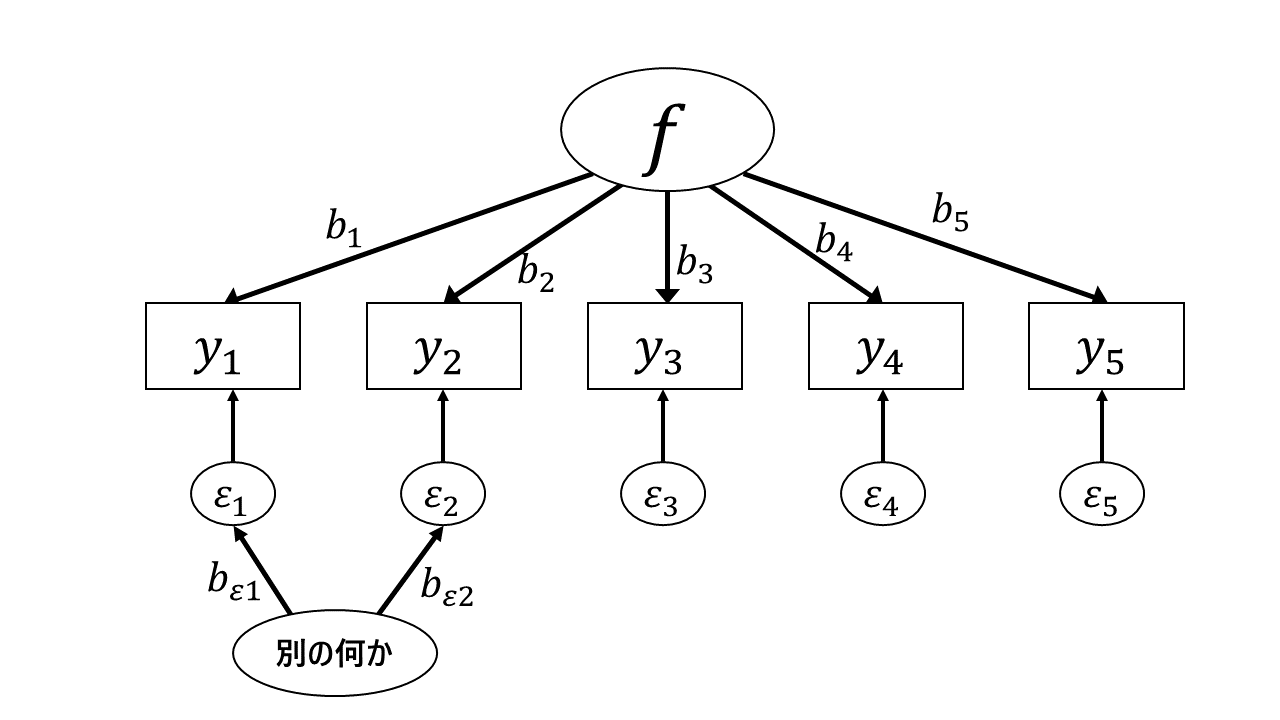
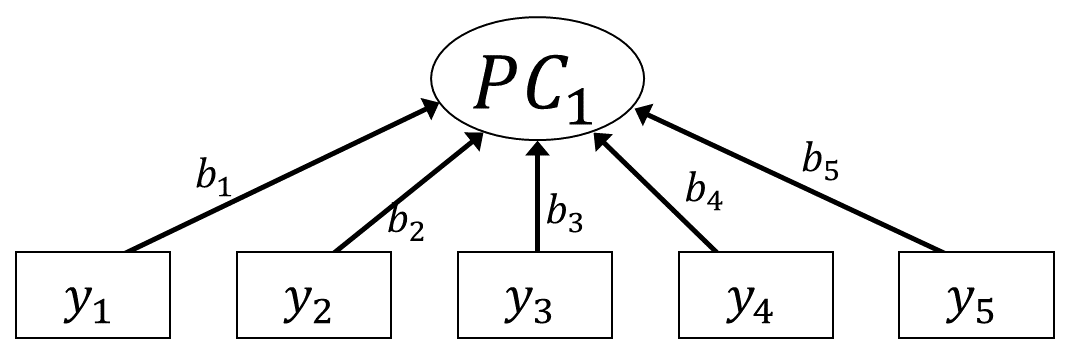
因子分析では，こうした一連の項目に関して共通する潜在的な特性値によって回答が決まっていると考えます。これをグラフィカルモデルで表すと以下のようになります。

グラフィカルモデルでは，潜在変数は楕円で表すのが一般的です。図 6.1 に関して，項目ごとに見るとこれは回帰分析モデルのように表すことができそうです。例えば項目Q1_11は，説明変数を「外向性」 $f_p$ として，対応する回帰係数を $b_{11}$ （添字は”11”の一つだけ）とすると $\begin{aligned} y_{p,11} = f_p b_{11} + \varepsilon_{p,11} \end{aligned} \qquad(6.1)$ と書くことが出来ます。この表現で言えば，回帰分析の説明変数に当たるものが $x_p$ から $f_p$ に変わっているだけです。同様にして，他の項目も $\begin{aligned} \begin{split} y_{p,12} &= f_{p}b_{12} + \varepsilon_{p,12} \\ y_{p,13} &= f_{p}b_{13} + \varepsilon_{p,13} \\ y_{p,14} &= f_{p}b_{14} + \varepsilon_{p,14} \\ y_{p,15} &= f_{p}b_{15} + \varepsilon_{p,15} \end{split} \end{aligned} \qquad(6.2)$ と表すことが出来ます。つまり，因子分析は項目レベルで見ると説明変数が潜在変数になった回帰分析なのです。なお，因子分析では本来回帰分析と同じように結果変数 $y$ は連続量（間隔尺度か比率尺度）を考えています。実際に心理尺度で得られる回答（項目レベル）はカテゴリカル変数であり間隔尺度である保証はないのですが，とりあえず今はポリシリアル相関のときと同じように $y$ は回答の背後の潜在変数だと考えるか，間隔尺度だと仮定されたものと考えておいてください。

ここまでは実際のデータに合わせて説明をしてきましたが，以後の説明ではもう少し一般化して説明していきます。ということで，ここで今後登場する添字を説明しておきます。なお，以下の記号について小文字は一つの値を，大文字は総数を表しているものとします。

[ $p$ ] 回答者の番号(person)を表します。（ $p=1,2,\cdots,P-1, P$ ）
[ $i$ ] 項目の番号(item)を表します。（ $i=1,2,\cdots,I-1, I$ ）

(6.1)および(6.2)式では，項目 $i$ は11, 12, 13, 14, 15と対応しています。この表記を用いると，回答者 $p$ の項目 $i$ に対する回答は以下のように表されます。

$y_{pi} = f_{p}b_{i} + \varepsilon_{pi} \qquad(6.3)$

ただ，いちいち $p$ を書いているとちょっと面倒なので，Chapter 5のときと同じように，回答者の要素についてはベクトル表記にしておきます。 $\symbf{y}_i=\begin{bmatrix}y_{1i} & y_{2i} & \cdots & y_{P-1,i} & y_{Pi}\end{bmatrix}^\top$ ， $\symbf{f}=\begin{bmatrix}f_{1} & f_{2} & \cdots & f_{P-1} & f_{P}\end{bmatrix}^\top$ ， $\symbf{\varepsilon}_i=\begin{bmatrix}\varepsilon_{1i} & \varepsilon_{2i} & \cdots & \varepsilon_{P-1,i} & \varepsilon_{Pi}\end{bmatrix}^\top$ として， $\begin{aligned} \begin{bmatrix} y_{1i} \\ y_{2i} \\ \vdots \\ y_{Pi} \end{bmatrix} &= \begin{bmatrix} f_1 \\ f_2 \\ \vdots \\ f_P \end{bmatrix}b_i + \begin{bmatrix} \varepsilon_{1i} \\ \varepsilon_{2i} \\ \vdots \\ \varepsilon_{Pi} \end{bmatrix} \\ \longrightarrow \symbf{y}_i &= \symbf{f}b_{i} + \symbf{\varepsilon}_i \end{aligned} \qquad(6.4)$ としておきます。

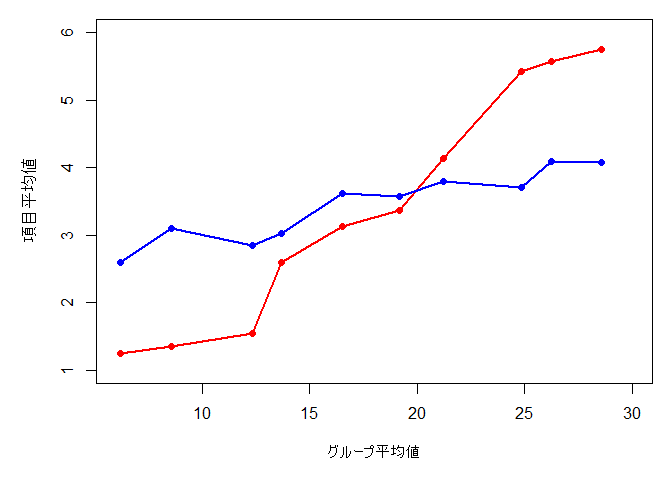
因子分析モデルでは，各個人の特性値の強さ（ $f_{p}$ ）を因子得点 (factor score)，回帰係数（ $b_i$ ）を因子負荷 (factor loading)と呼びます。因子負荷が高い項目ほど，その人の回答が因子得点の高低と強く関係しています。これは，合計点をX軸に，グループごとの平均値をY軸に置いたトレースラインの右上がり度の強さと近いものです。そして一般的には，右上がりの項目ほどI-T相関も高くなります。図 6.2 でいえば，赤い項目の方が強い右上がりになっているため，青い項目よりも因子負荷が高い項目だと考えることが出来ます。

なおグラフィカルモデルでは図 6.3 のように，因子負荷の強さを矢印の横に書くのが一般的です。

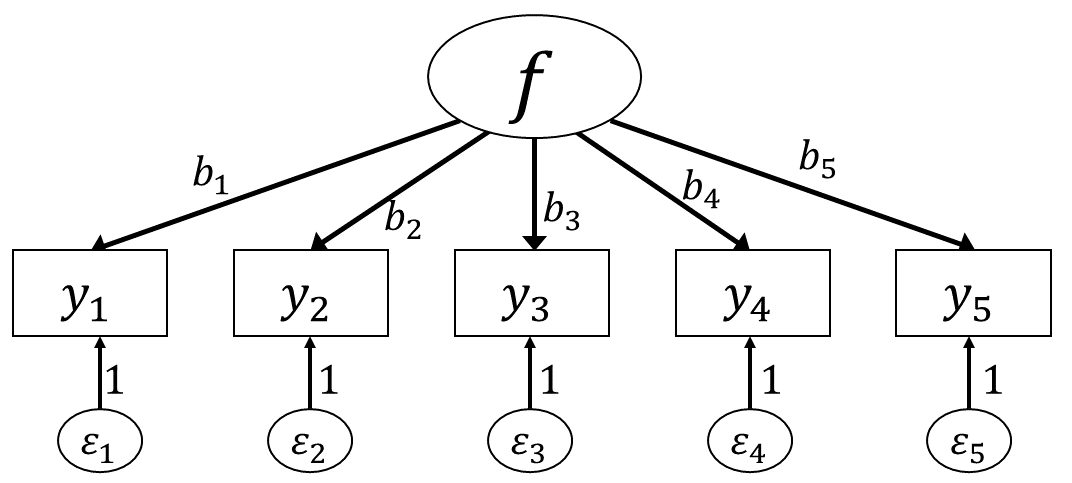
また，因子分析では誤差 $\varepsilon$ のほうも「因子」として取り扱います。複数の項目に共通する成分（ $\symbf{f}$ ）を共通因子 (common factor)，各項目に特有の成分（あるいは共通因子で説明されなかった残り）を独自因子 (unique factor)と呼び，各項目への回答はこの2種類の因子の和のみによって表されていると考えるわけです。したがって，先程示した因子分析モデルの基本である (6.4)式における $\symbf{\varepsilon}_{i}$ は，実際には「誤差」ではなく「もう一つの説明変数」であると考えることがあります。ということで，(6.4)式は厳密には以下のような形をしています。 $\symbf{y}_i = \symbf{f}b_{i} + \symbf{\varepsilon}_i u_{i} \overbrace{+ 0}^{\mathrm{error}}$ ここで $u_{i}$ は，独自因子に対する因子負荷を表しています。このように，因子分析モデルでは回帰分析で言うところの「誤差」は0と考えることが多いようです。 …とはいえ，実際には $\symbf{\varepsilon}_i$ と「誤差」は区別のしようが無いので，独自因子得点を誤差として扱ってしまうことも多々あります。というかその方が多いかもしれません。

ということでグラフィカルモデルにもこの独自因子を書き込むと，図 6.4 のようになります。ただし独自因子の因子負荷 $u_{i}$ を自由に推定しようとすると，独自因子得点 $\symbf{\varepsilon}_i$ との間にまたスケールの問題が生じてしまい解が一つに決まらない（例えば全ての $u_{i}$ を2倍にして $\symbf{\varepsilon}_i$ を0.5倍にしても良くなってしまう）ため，通常は $u_{i}=1$ に固定されます。

実際に論文などに載せる場合，独自因子の因子負荷はどうせ固定されるのだから，矢印の横の「1」は省略されることが多いです。更にいうと，因子分析ではそもそも共通因子にのみ関心があることが圧倒的に多いので，独自因子自体を省略する形（つまり図 6.3 ）で表されることも多いです。

6.1.1 因子負荷の意味と項目間相関

数理的な表現は後ほど示しますが，因子分析では基本的に，観測変数（項目）間の相関関係をもとに因子負荷（と独自因子の分散）を推定します。そこで，まずは因子負荷と項目間相関がどのように関連しているかを感覚的に説明しておきましょう。

まず，図 6.4 に示されているように，因子負荷は「その項目と共通因子の関連（相関関係）の強さ」を表しています。実際にこれまでに出てきた因子分析のモデル式（6.3 式など）では，因子負荷が高い項目ほど「その項目への回答の高低」が「因子得点の高低」と高い相関を持つことが示されていました。結果として，因子負荷が高い項目というのは，同じ共通因子の影響を受ける他のすべての項目と相関が高いことになります。この事実から考えると，因子負荷が高い項目どうしの相関は，因子負荷が低い項目どうしの相関よりも高いということが考えられるのです。

因子分析が「観測変数（項目）間の相関関係をもとに因子負荷（と独自因子の分散）を推定」するというのは，上述の関係から逆算するように，他の項目との相関が高い項目ほど因子負荷が高めの値になるように推定を行っている，ということを意味しています。

6.1.2 位置・スケールの不定性

因子分析では，回帰分析と違って説明変数にあたるもの（因子得点： $\symbf{f}$ ）が直接観測できない潜在変数 (latent variable)になっています。説明変数が潜在変数のときには，ちょっと困ったことが起こります。それは変数のスケールの問題です。いま，因子 $\symbf{f}$ には身長や体重のときのような「単位」というものがありません。例えばリッカート尺度の項目が1から5の5件法であったとしても，それは尺度を作った人や分析者が勝手に決めたことであって，同じ項目を7件法で尋ねたり50件法で尋ねたりしても，理論的にはなんの問題もありません（実用的には問題あるかも）。

ということで，100点満点のテストの点数を500点満点に換算して扱うように， $\symbf{f}$ の値を5倍して，更に10点のゲタをはかせたものを $\symbf{f}'=5\symbf{f}+10$ とします。これを使うと，先程の回帰式は $\begin{align} \begin{split} \symbf{y}_i &= \symbf{f}b_{i} + \symbf{\varepsilon}_i \\ &= (5\symbf{f}+10)(0.2b_{i}) + (\symbf{\varepsilon}_i-2b_{i}) \\ &= \symbf{f}'b'_{i} + \symbf{\varepsilon}'_i \end{split} \end{align}$ と変形が可能です。つまり $\symbf{f}$ のスケールが変わることで $b'_{i}=0.2b_{i}$ および $\symbf{\varepsilon}'_i=\symbf{\varepsilon}_i-2b_{i}$ という新しい解が得られてしまいます。このままでは回帰係数を一意に求めることが出来ないので，通常因子分析モデルでは，因子の分散 $\sigma_{\symbf{f}}^2=1$ かつ平均0という制約を置いています²。これに加えて，通常因子分析で考える潜在変数は正規分布に従う連続量であると仮定されます。これらをまとめると，因子分析では $\symbf{f} \sim N(0,1)$ という仮定が置かれていることになります。言い換えると，因子分析で推定される因子得点 $\symbf{f}$ は，特に指定がなければ標準化された値として得られるということです。

そしてこの問題は，観測変数 $y$ の値のスケールに客観的な単位が存在しないケース（例えば心理尺度など）についても同様のことがいえます。これも100点満点のテストの点数を500点満点に換算して扱うように，例えば5件法のリッカート尺度の得点を5, 10, 15, 20, 25と5刻みにしても問題は無いはずです。ということで $\symbf{y}'_i=5\symbf{y}_i$ として回帰式を変形させてみると， $\begin{aligned} \begin{split} \symbf{y}'_i &= 5\symbf{y}_i \\ &= 5\symbf{f}b_{i} + 5\symbf{\varepsilon}_i \\ &= \symbf{f}\times 5b_{i} + 5\symbf{\varepsilon}_i \\ &= \symbf{f}b''_{i} + \symbf{\varepsilon}'_i \end{split} \end{aligned}$ ということで， $b''_{i}=5b_{i}$ および $\symbf{\varepsilon}'_i=5\symbf{\varepsilon}_i$ という新しい解が得られてしまいます。このように，因子分析の解は回答側のスケールの影響も受けてしまうため，通常は各項目の回答は全て標準化された値を使用します。説明変数（ $\symbf{f}$ ）も結果変数（ $\symbf{y}_i$ ）も標準化されているという意味では，因子負荷は標準偏回帰係数のように解釈することができる，というわけです³。

6.2 因子分析モデルの一般化

回帰分析的に因子分析を見ると，独自因子は誤差のようなものなのでなるべくその影響は少ないほうが良い，といえます。極端な例を考えてみましょう。因子負荷 $b_i=0$ の項目があるとすると，その項目の因子分析モデル式は $\begin{aligned} \begin{split} \symbf{y}_i &= \symbf{f}\times 0 + \symbf{\varepsilon}_i \\ &= \symbf{\varepsilon}_i \end{split} \end{aligned} \qquad(6.5)$ となります。共通因子の影響を全く受けること無く独自因子のみで回答が決定している状態です。因子得点 $f_p$ を推定する上では何の情報も持ち合わせていないこの項目は，あってもなくても同じです。この項目に高い点数をつけていても低い点数をつけていても， $f_p$ には何も関与していないのです。ということで，基本的には因子分析では共通因子の影響が多い方が望ましいわけです。

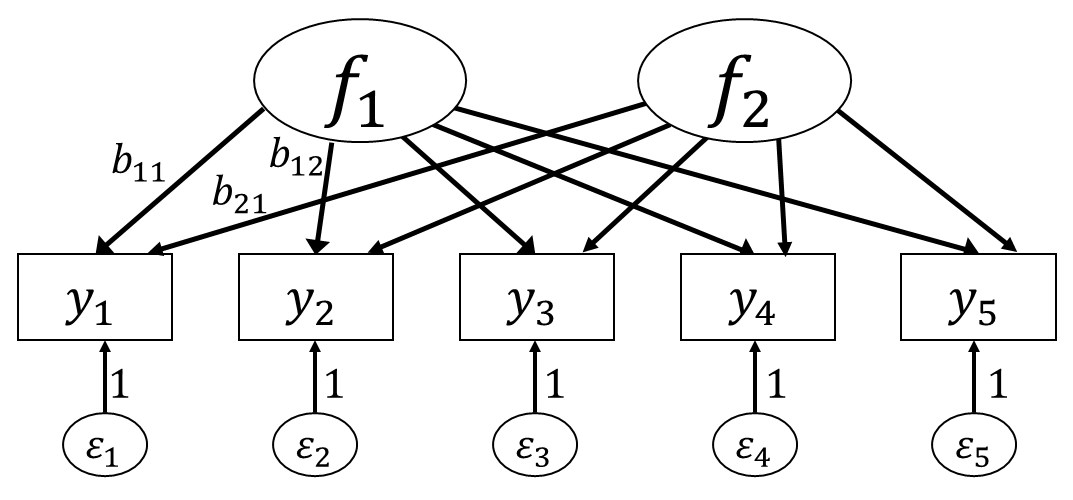
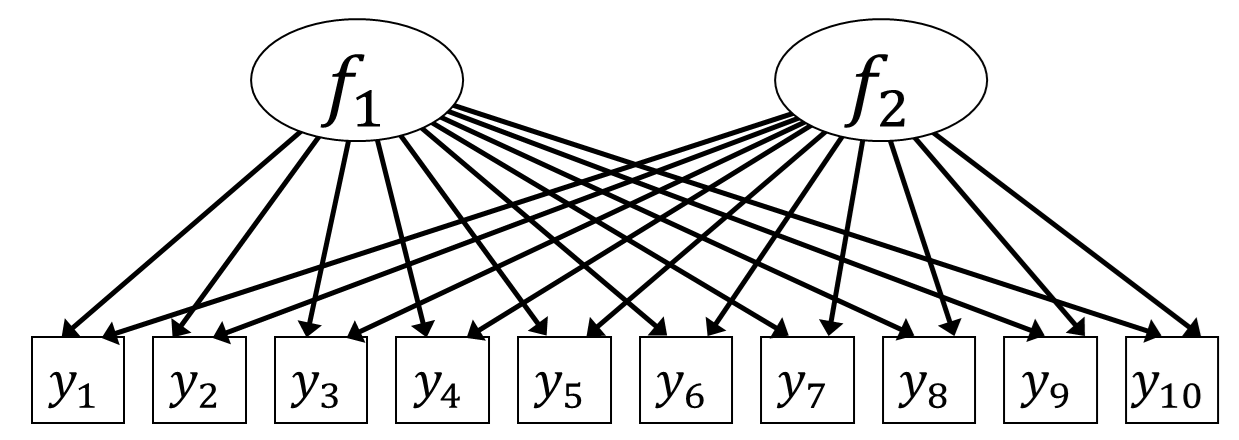
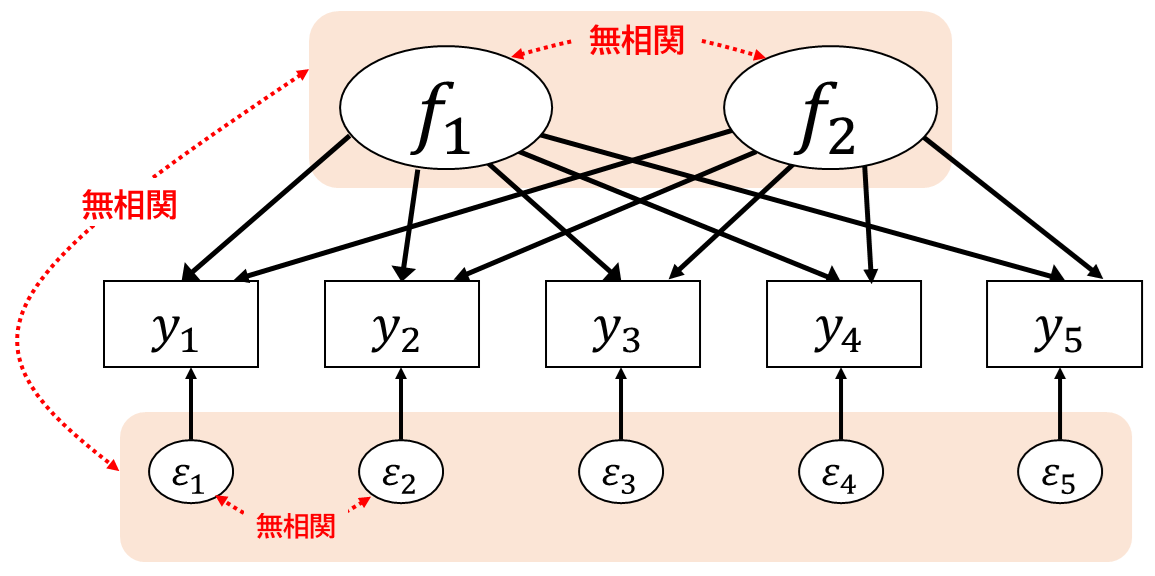
回帰分析では， $y$ に占める誤差分散の割合を減らし予測の精度を上げるために，複数の説明変数を用いることができました。因子分析でも同様に，複数の説明変数＝共通因子がある状態を考えることができます。ここでは，5項目が2つの共通因子の影響を受けている，と考えてみましょう。グラフィカルモデルでは図 6.5 のような状態です。なお，因子番号を表す添字はtraitの頭文字 $t~(t=1,2)$ としておきます。

当然ながら，因子1の項目1に対する因子負荷 $b_{11}$ （添字は2つ：1と1）と因子2の因子負荷 $b_{21}$ は異なります。したがって， $\symbf{y}_i$ に関する因子分析モデルは $\symbf{y}_i = \symbf{f}_1b_{1i} + \symbf{f}_2b_{2i} + \symbf{\varepsilon}_i \qquad(6.6)$ となります。

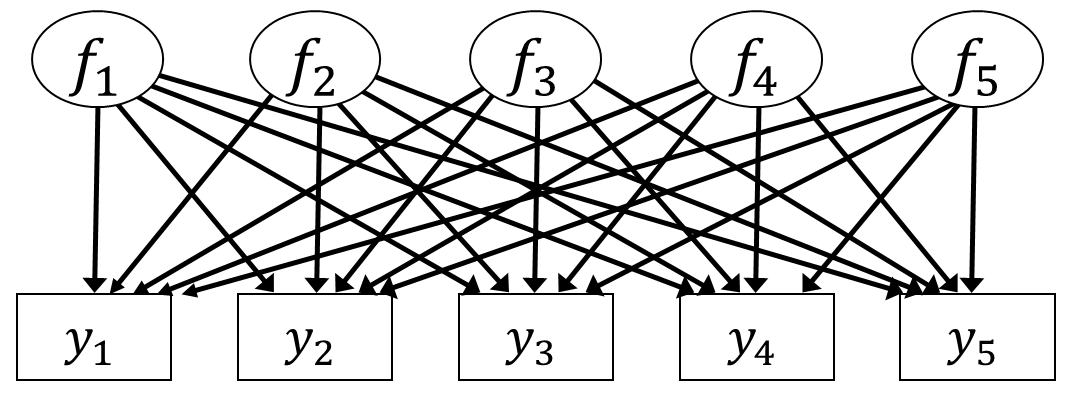
もちろん因子の数はいくつでも良いので，更に一般化して $T$ 個の因子がある場合を考えると， $\symbf{y}$ に関する因子分析モデルは $\begin{aligned} \begin{split} \symbf{y}_i &= \symbf{f}_1b_{1i} + \symbf{f}_2b_{2i} + \cdots + \symbf{f}_Tb_{Ti} + \symbf{\varepsilon}_i \\ &= \begin{bmatrix} \symbf{f}_1 & \symbf{f}_2 & \cdots & \symbf{f}_T \end{bmatrix} \begin{bmatrix} b_{1i} \\ b_{2i} \\ \vdots \\ b_{Ti} \end{bmatrix} + \symbf{\varepsilon}_i \\ &= \symbf{F}\symbf{b}_i + \symbf{\varepsilon}_i \end{split} \end{aligned} \qquad(6.7)$ と書くことが出来ます。

6.3 とりあえずやってみよう

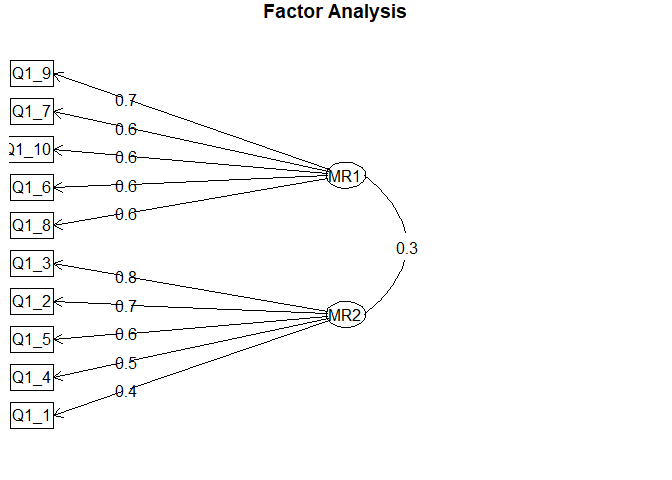
このあたりでひとまずRで因子分析をやってみて，実際のデータから何が出てくるのかをみてみたいと思います。 Rにはデフォルトでfactanal()という関数が用意されているのですが，ちょっとモダンな方法に関して不十分なので，もっと色々できる関数を使用します。 psychパッケージにあるfa()という関数を使用しましょう。 fa()関数では，因子数をnfactorsという引数で与えます。今回はQ1_1からQ1_10の10項目に対して2因子に設定してみました。つまり，図 6.6 のモデルに対して因子負荷（全ての矢印の係数）を計算してみます。

コード 6.3: とりあえず因子分析

library(psych)
# まずは2因子でやってみます
res_fa <- fa(dat[, paste0("Q1_", 1:10)], nfactors = 2)
res_fa

Factor Analysis using method =  minres
Call: fa(r = dat[, paste0("Q1_", 1:10)], nfactors = 2)
Standardized loadings (pattern matrix) based upon correlation matrix
        MR1   MR2   h2   u2 com
Q1_1  -0.08  0.42 0.16 0.84 1.1
Q1_2   0.00  0.68 0.47 0.53 1.0
Q1_3  -0.03  0.77 0.58 0.42 1.0
Q1_4   0.14  0.46 0.27 0.73 1.2
Q1_5   0.03  0.61 0.38 0.62 1.0
Q1_6   0.57 -0.05 0.31 0.69 1.0
Q1_7   0.64 -0.02 0.40 0.60 1.0
Q1_8   0.55  0.02 0.31 0.69 1.0
Q1_9   0.68  0.00 0.46 0.54 1.0
Q1_10  0.57  0.06 0.35 0.65 1.0

                       MR1  MR2
SS loadings           1.87 1.83
Proportion Var        0.19 0.18
Cumulative Var        0.19 0.37
Proportion Explained  0.51 0.49
Cumulative Proportion 0.51 1.00

 With factor correlations of 
     MR1  MR2
MR1 1.00 0.32
MR2 0.32 1.00

Mean item complexity =  1
Test of the hypothesis that 2 factors are sufficient.

df null model =  45  with the objective function =  2.14 with Chi Square =  5190.53
df of  the model are 26  and the objective function was  0.16 

The root mean square of the residuals (RMSR) is  0.04 
The df corrected root mean square of the residuals is  0.05 

The harmonic n.obs is  2432 with the empirical chi square  311.44  with prob <  1.1e-50 
The total n.obs was  2432  with Likelihood Chi Square =  379.19  with prob <  2.2e-64 

Tucker Lewis Index of factoring reliability =  0.881
RMSEA index =  0.075  and the 90 % confidence intervals are  0.068 0.082
BIC =  176.48
Fit based upon off diagonal values = 0.98
Measures of factor score adequacy             
                                                   MR1  MR2
Correlation of (regression) scores with factors   0.87 0.88
Multiple R square of scores with factors          0.76 0.78
Minimum correlation of possible factor scores     0.51 0.56

6.3.1 因子負荷量

Standardized loadings (pattern matrix) based upon correlation matrix
        MR1   MR2   h2   u2 com
Q1_1  -0.08  0.42 0.16 0.84 1.1
Q1_2   0.00  0.68 0.47 0.53 1.0
Q1_3  -0.03  0.77 0.58 0.42 1.0
Q1_4   0.14  0.46 0.27 0.73 1.2
Q1_5   0.03  0.61 0.38 0.62 1.0
Q1_6   0.57 -0.05 0.31 0.69 1.0
Q1_7   0.64 -0.02 0.40 0.60 1.0
Q1_8   0.55  0.02 0.31 0.69 1.0
Q1_9   0.68  0.00 0.46 0.54 1.0
Q1_10  0.57  0.06 0.35 0.65 1.0

fa()関数では，データフレームを与えると，まずそのデータフレームに対してcor()関数の要領で相関行列を計算します。そしてその相関行列から因子負荷行列を出しています。左のMR1およびMR2という部分が因子負荷（ $\symbf{B}^\top$ ）を表しています⁴。論文では，良く「値が一定以上のところを太字にする」や「一定以下のところを空白にする」という形で記載されています。試しに値が0.4以上のところを太字にすると，表 6.1 のようになります。

表 6.1: 因子負荷の表

	MR1	MR2
Q1_1	-0.08	0.42
Q1_2	0.00	0.68
Q1_3	-0.03	0.77
Q1_4	0.14	0.46
Q1_5	0.03	0.61
Q1_6	0.57	-0.05
Q1_7	0.64	-0.02
Q1_8	0.55	0.02
Q1_9	0.68	0.00
Q1_10	0.57	0.06

また，print()関数に引数sort=TRUEを与えると，因子負荷行列がいい感じになるように項目を並び替えてくれます。

print(res_fa, sort = TRUE)

Factor Analysis using method =  minres
Call: fa(r = dat[, paste0("Q1_", 1:10)], nfactors = 2)
Standardized loadings (pattern matrix) based upon correlation matrix
      item   MR1   MR2   h2   u2 com
Q1_9     9  0.68  0.00 0.46 0.54 1.0
Q1_7     7  0.64 -0.02 0.40 0.60 1.0
Q1_10   10  0.57  0.06 0.35 0.65 1.0
Q1_6     6  0.57 -0.05 0.31 0.69 1.0
Q1_8     8  0.55  0.02 0.31 0.69 1.0
Q1_3     3 -0.03  0.77 0.58 0.42 1.0
Q1_2     2  0.00  0.68 0.47 0.53 1.0
Q1_5     5  0.03  0.61 0.38 0.62 1.0
Q1_4     4  0.14  0.46 0.27 0.73 1.2
Q1_1     1 -0.08  0.42 0.16 0.84 1.1

（以下略）

出力を見ると，確かに因子負荷行列の行の並び順が変わっています。一番上には「他の因子より因子1への負荷が最も高い項目のうち，MR1が最も高い項目」がおかれ，後もそれに続いています。つまり全ての項目を「どれか一つの因子のグループに属するとしたら」という感じで並び替えてくれるわけです。論文に載せる際なども，これで表示される順にすると見やすいのではないかと思います。

表 6.2: 因子負荷の表（並べ替え後）

	MR1	MR2
Q1_9	0.68	0.00
Q1_7	0.64	-0.02
Q1_6	0.57	-0.05
Q1_10	0.57	0.06
Q1_8	0.55	0.02
Q1_3	-0.03	0.77
Q1_2	0.00	0.68
Q1_5	0.03	0.61
Q1_4	0.14	0.46
Q1_1	-0.08	0.42

また，psychパッケージのfa.diagram()関数を使うと，図 6.7 のようにグラフィカルモデル的なものを描いてくれます。もちろんそのまま論文に載せたりできるレベルではないですが，項目と因子の関係をざっと眺めたいときには役に立ちそうです。

コード 6.4: 一応グラフィカルモデル的なものを出す

fa.diagram(res_fa, cut = 0.3)

デフォルトでは各項目には「最も高い因子負荷を持つ因子」のみ矢印を引くよう(simple=TRUE)ですが，引数simple=FALSEとすることで複数因子からの矢印を引くことも可能です。ただ数字が重なったりして見にくいかもしれません。また，引数cutは「その絶対値以下の因子負荷や因子間相関の矢印は引かない」というものです。なので先程のコードでは，因子負荷や因子間相関が0.3以下のものは省略されている…と言っても今回は「最も高い因子負荷」に0.3以下のものが無いので違いが分かりませんが…。

6.3.2 因子負荷を「解釈」する

因子分析は相関行列を対象にした分析法ですが，その目的の一つは項目をグルーピングするとともに，その背後にある共通因子が何者であるかを解釈してあげることです。例えば共通因子MR1はQ1_6からQ1_10に対して高い負荷を持っていた一方で，Q1_1からQ1_5に対する因子負荷は低い値でした。そのため，MR1を「解釈」するうえでは，Q1_6からQ1_10に共通する要素のみを考えたら良く，Q1_1からQ1_5は気にしなくて良いといえます。

ということで，実際にQ1_6からQ1_10の質問項目を見てみると，

Am exacting in my work. （自分の仕事には厳しく要求する。）
Continue until everything is perfect. （完璧になるまでやり続ける。）
Do things according to a plan. （計画に基づき行動する。）
Do things in a half-way manner. （【逆転】物事を中途半端に行う。）
Waste my time. （【逆転】時間を無駄にする。）

という5つです。逆転項目も含めて，これらに共通する要素を考えると（人によって感じ方は異なると思いますが）MR1には例えば「計画性」や「慎重さ」のような名前が考えられるでしょう。ちなみに，公式にはこれらの項目の背後にあるものは「誠実性 (conscientiousness)」と呼ばれています。

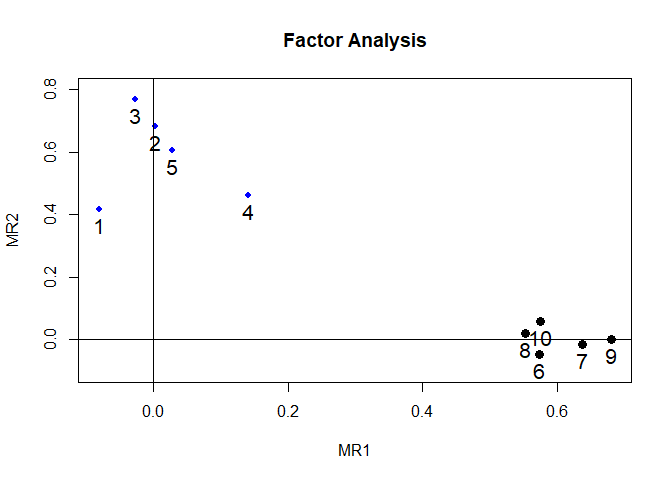
因子の「解釈」の意味を少し別の視点から見もてみましょう。項目をグルーピングする場合には，単純に因子負荷の値が似ている項目は距離が近いと考えることができます。ということで，先ほど得られた因子負荷をもとに散布図を書いてみます。図 6.8 はX軸にMR1を，Y軸にMR2の値をとった各項目の因子負荷量のプロットです。psychパッケージにあるfa.plot()関数で簡単に描くことが出来ます⁵。

コード 6.5: 因子負荷のプロット

fa.plot(res_fa)

こうして見ると，確かにQ1_1からQ1_5のグループと，Q1_6からQ1_10のグループに分かれているように見えますね。そしてQ1_1からQ1_5のグループではMR1の値がゼロに近く，反対にQ1_6からQ1_10のグループではMR2の値がゼロに近いので，各点は軸の近くに位置しています。いま，MR2の軸に名前をつける（「解釈」する）ことを考えてみましょう。これは「どのような内容の項目においてMR2の値が大きくなるか」を考えることなので，MR2の値が大きい項目（ここではQ1_1からQ1_5）の間に共通する要素を探せば良いはずです。このとき重要なのは，Q1_6からQ1_10はMR2の値がほぼゼロなので，MR2を「解釈」する際には考える必要はなさそうだ，という点です。反対にMR1の「解釈」においてはQ1_1からQ1_5を無視することができそうです。このように，各項目の因子負荷がどちらか一方にだけ高い値で，もう一方の因子に対してはほぼゼロになっていると，MR1とMR2はそれぞれ異なるグループに共通する要素を反映したものとして，ほぼ独立に「解釈」することができるわけです。

…ということで，因子分析の目的からすると，得られる因子負荷行列においては一つの項目はなるべく一つの因子だけに高い負荷を持つという状態が望ましいとされています。これを単純構造 (simple structure) と呼びます。一方で，もしも単純構造から外れた項目，つまり「複数の因子に高い負荷量をもつ項目」があると，複数の共通因子の間に共通項があることを加味した解釈が必要になってしまい，かなり大変そうだということが見えてきます。

因子負荷量の出力の一番右の列にあったcomはこの単純構造の程度を表した指標です。これが1に近いほど，その項目は1つの因子にのみ高い負荷を持っているという判断ができます。今回の結果では，Q1_4が1.2と最も高い値になっています。たしかに，他の項目と比べるとMR1とMR2の差が小さいようです。が，実際のところ1.2は相当マシな値です。どれくらい大きかったら気をつけたら良いか，という基準は特に無いですが…

6.3.3 因子の解釈と項目の選定

ということで，無事因子負荷行列が計算できたら，表 6.2 や（2因子なら）図 6.8 をもとに，それぞれの因子に負荷が高い項目のグループを見て，共通の要因を見つけてあげて，因子に名前をつける（「解釈」する）ことになります。ここは領域の知識などが要求されるところです。なので同じデータであっても人によっては異なる名前をつける可能性があります。また，そもそも共通する内容が見当たらないような項目が同じグループに入ってしまうことも実際には多々あります。そのような場合には，解釈しやすいグルーピングを求めて共通因子の数を変えるということも検討する必要があります（詳細は Section 6.11）。そして解釈した因子の名前が真っ当かどうかは，査読者ないし読者が判断することになります。 因子の名前に客観的な「正解」というものは無いので，納得させられたら勝ちなわけです。

また，当然ながら因子分析の結果は手元のデータから得られる，つまり使用したデータによって結果は異なるものです。そのため，先行研究で作成された尺度をそのまま用いた場合でも，因子構造が同じものが得られるとは限りません。特に先行研究と属性の異なる集団でデータを集めた場合や，古い尺度を使用する場合には改めて因子分析を行い，同じ因子構造が得られることを確認してから分析を進めるのが良いでしょう。

今回のデータのように各項目がほぼ一つの因子のみに高い負荷を持っている場合には解釈は容易なのですが，多くの実データではきっと複数の因子に高い負荷を持っている項目や，どの因子にも高い負荷を持っていない項目が出現するでしょう。このような場合，とりあえず単純構造を求めて厄介な項目は削除するという手続きを取っている研究が結構多く見られます。

どの因子にも高い負荷を持っていない項目は，言い換えると独自性が高い項目であり，因子得点を算出する上ではあってもなくてもあまり変わらないと予想されます。したがって，項目数を減らしたい場合などには優先的に除外対象としたら良いでしょう。一方で複数の因子に高い負荷を持っている項目を削除してしまうかは結構悩ましいところです。実際の尺度作成論文では，「複数の因子に0.3以上の負荷を持つ項目は削除した」的な手続きが書かれていることがよくあります。この手続きが正しいかどうかは，時と場合によると思われます。

一般的に心理尺度を作成する場合には，なるべく「みんなが使いやすいモノサシ」を開発しようとしています。そして，共通のモノサシを用いることで異なる研究間での結果を比較可能にしようと考えたりしています。そのため，尺度得点としては因子得点ではなく和得点を用いることが多いです。因子得点を用いた場合，データ毎に因子構造が変わってしまうので異なるデータ間での因子得点の比較などは難しくなってしまいます。さて，下位概念ごとの和得点を計算する場合，直感的には「その因子に高い負荷を持っている項目の和」を使えば良さそうです。この時に，複数の因子に高い負荷を持つ項目があると，その項目の回答は複数の下位概念でカウントされてしまうため，実質的に他の項目の倍の価値を持ってしまうことになります。こうした問題点を避けるという目的であれば，複数の因子に高い負荷を持つ項目は使わずに，もっと使いやすい（単純構造な）項目を使って尺度を構成するのは悪くない方法だと思います。

一方で，尺度開発が目的ではない（例えば人に使ってもらうというよりは単純に項目をグルーピングして共通項を取り出したい，他の人が作った尺度を使うが先行研究と比較する予定はない，などの）場合には，項目数を減らす必要も無ければ和得点を使う必要もありません。因子得点を計算する上では，複数の因子に高い負荷を持っている項目も重要（むしろきっと共通性が高いのでかなり役に立つ）です。このような場合に，「他の研究でもやっているから」という理由で安直に「複数の因子に高い負荷を持っている項目は削除」としてしまうのは悪手と言えるでしょう。

また，構造的な問題として「1項目だけが高い負荷を持っている因子」は通常使用しません⁶。因子分析の目的は「複数の項目に共通して影響する潜在変数を抽出する」ことなので，他のどの項目とも独立している一匹狼に対して「因子」という見方はあまりしないのです。統計的にも，1項目だけの因子の場合，その項目への回答と因子得点は完全に一致するため，標準化してしまえば回答値をそのまま使えば良いということがいえます。ただし，それはそれで他の項目とは独立した「何か」を測定している項目ではあるので，この場合も削除するかはよく考えてください。

以上の話は，全て統計的な視点からのことです。実際に項目を削除するかは，構成概念と項目の内容との関係を改めて精査したり，因子の解釈においてノイズになっていないかを検討したりといった，妥当性の内容的な側面からのチェックも忘れずに行ってください。

6.4 モデルパラメータによる相関係数の表現

Section 6.1.1 では「同じ共通因子の影響を受ける他の項目との相関が高い項目ほど因子負荷が大きくなる」と説明をしました。次節では，因子負荷 $\symbf{B}$ を計算する方法を数理的に紹介していくのですが，これを理解するために，ここでは項目間の相関行列がモデルパラメータでどのように表現できるかを確認しておきます。ということで，まずは因子数が1の場合で因子分析モデル内のパラメータと観測変数間の相関係数の関係性を確認してみましょう。

6.4.1 1因子の場合

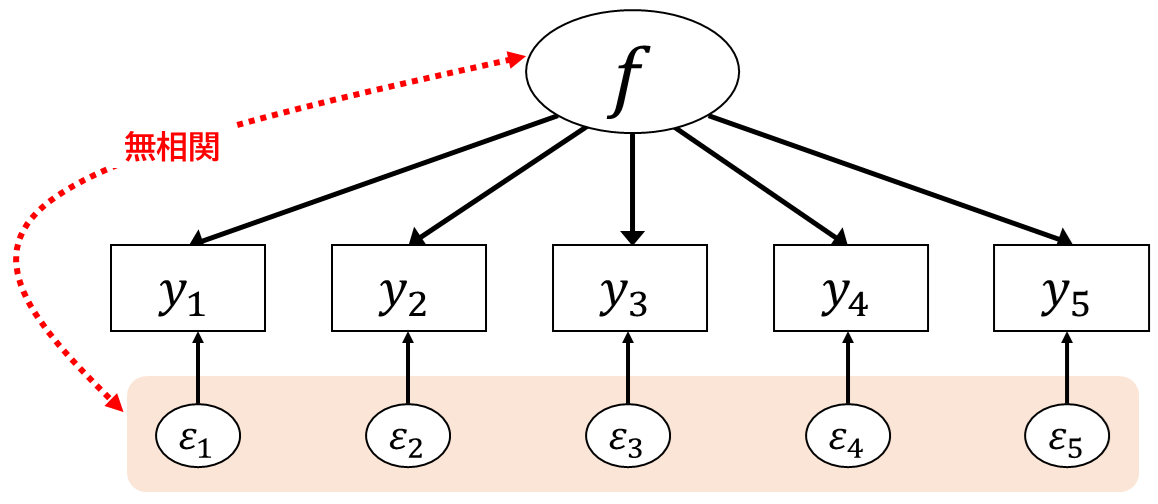
図 6.4 に示した1因子の因子分析モデルにおいて，2つの項目に対する回答のモデル上での相関関係がどのように表されるかを考えてみます。まず，各項目の回答は標準化されたものという前提に立つと，変数間の共分散と相関係数は一致します。したがって，ある項目への回答 $\symbf{y}_i$ と別の項目への回答 $\symbf{y}_j~(i\neq j)$ の共分散 $\sigma_{\symbf{y}_i,\symbf{y}_j}$ および相関係数 $r_{\symbf{y}_i,\symbf{y}_j}$ を展開してみると $\begin{aligned} \begin{split} \sigma_{\symbf{y}_i,\symbf{y}_j} = r_{\symbf{y}_i,\symbf{y}_j} &= \sigma_{(b_{i}\symbf{f} + \symbf{\varepsilon}_i),(b_{j}\symbf{f} + \symbf{\varepsilon}_j)} \\ &= \sigma_{(b_{i}\symbf{f}),(b_{j}\symbf{f})} + \sigma_{(b_{i}\symbf{f}),(\symbf{\varepsilon}_j)} + \sigma_{(b_{j}\symbf{f}),(\symbf{\varepsilon}_i)} + \sigma_{\symbf{\varepsilon}_i,\symbf{\varepsilon}_j} \\ & = b_{i}b_{j}\sigma_{\symbf{f}}^2 + \sigma_{(b_{i}\symbf{f}),(\symbf{\varepsilon}_j)} + \sigma_{(b_{j}\symbf{f}),(\symbf{\varepsilon}_i)} + \sigma_{\symbf{\varepsilon}_i,\symbf{\varepsilon}_j} \end{split} \end{aligned} \qquad(6.8)$ となります。ここで，ある項目の共通因子成分と別の項目の独自因子成分は，通常の回帰分析と同じように無関係（共分散ゼロ）と見なすことができるため， $\sigma_{(b_{i}\symbf{f}),(\symbf{\varepsilon}_j)} = \sigma_{(b_{j}\symbf{f}),(\symbf{\varepsilon}_i)} = 0 \qquad(6.9)$ が成り立ちます。

ということで，(6.9)式は少し整理されて $r_{\symbf{y}_i,\symbf{y}_j} = b_{i}b_{j}\sigma_{\symbf{f}}^2 + \sigma_{\symbf{\varepsilon}_i,\symbf{\varepsilon}_j}$ となります。そして先程説明したように，因子の分散 $\sigma_{\symbf{f}}^2$ は1に固定するという制約が置かれています。したがって，2項目の相関係数は最終的に $r_{\symbf{y}_i,\symbf{y}_j} = b_{i}b_{j} + \sigma_{\symbf{\varepsilon}_i,\symbf{\varepsilon}_j} \qquad(6.10)$

つまり「因子負荷の積 $b_{i}b_{j}$ 」と「独自因子同士の共分散 $\sigma_{\symbf{\varepsilon}_i,\symbf{\varepsilon}_j}$ 」の和によって表すことが出来ます。ここで，独自因子同士の共分散 $\sigma_{\symbf{\varepsilon}_i,\symbf{\varepsilon}_j}$ はゼロとは限りません。図 6.4 のモデルで言えば，共通因子は「5項目全てに共通する成分」ですが，もしかしたら図 6.9 のように「5項目全てでは無いけれど2項目だけに共通する成分」などがまだ残っているかもしれません。

この状態では， $\sigma_{\symbf{y}_i,\symbf{y}_j}$ のときと同じ要領で $\sigma_{\symbf{\varepsilon}_i,\symbf{\varepsilon}_j}$ も2つの独自因子に対する因子負荷の積（ $b_{\varepsilon1}b_{\varepsilon2}\neq 0$ ）になってしまいます。

このままだと，観測された相関係数から因子負荷 $\symbf{b}$ を推定することができないので，推定できるようにするために「全ての項目が共通因子の影響を受けている」という仮定を置きます。この仮定が満たされている理想的な状況では，項目間で共通する成分は共通因子にすべて吸収されるため，残った独自因子同士の相関はゼロであることが期待されています。言い換えると，理想的な状況では2項目間の相関係数は因子負荷の積のみ（ $r_{\symbf{y}_i,\symbf{y}_j} = b_{i}b_{j}$ ）になることが期待されるので，これならば因子負荷の推定が可能となるのです。

同様にして，項目 $i$ の分散（＝項目 $i$ と項目 $i$ の共分散）は $\sigma_{\symbf{y}_i}^2 = \sigma_{\symbf{y}_i,\symbf{y}_i} = b_{i}^2 + \sigma_{\symbf{\varepsilon}_i}^2 \qquad(6.11)$ となります。つまり因子負荷の2乗と誤差分散の和になっています。

以上をまとめると，観測変数の相関行列 $\symbf{\Sigma}$ は以下のように因子分析のパラメータの関数に変換することが出来ます。 $\begin{aligned} \begin{split} \symbf{\Sigma} &=\begin{bmatrix} \sigma_{y_1}^2 & \sigma_{y_1,y_2} & \sigma_{y_1,y_3} & \sigma_{y_1,y_4} & \sigma_{y_1,y_5} \\ \sigma_{y_2,y_1} & \sigma_{y_2}^2 & \sigma_{y_2,y_3} & \sigma_{y_2,y_4} & \sigma_{y_2,y_5} \\ \sigma_{y_3,y_1} & \sigma_{y_3,y_2} & \sigma_{y_3}^2 & \sigma_{y_3,y_4} & \sigma_{y_3,y_5} \\ \sigma_{y_4,y_1} & \sigma_{y_4,y_2} & \sigma_{y_4,y_3} & \sigma_{y_4}^2 & \sigma_{y_4,y_5} \\ \sigma_{y_5,y_1} & \sigma_{y_5,y_2} & \sigma_{y_5,y_3} & \sigma_{y_5,y_4} & \sigma_{y_5}^2 \\ \end{bmatrix} \\ &= \begin{bmatrix} b_1^2+\sigma_{\symbf{\varepsilon}_1}^2 & b_1b_2 & b_1b_3 & b_1b_4 & b_1b_5 \\ b_2b_1 & b_2^2+\sigma_{\symbf{\varepsilon}_2}^2 & b_2b_3 & b_2b_4 & b_2b_5 \\ b_3b_1 & b_3b_2 & b_3^2+\sigma_{\symbf{\varepsilon}_3}^2 & b_3b_4 & b_3b_5 \\ b_4b_1 & b_4b_2 & b_4b_3 & b_4^2+\sigma_{\symbf{\varepsilon}_4}^2 & b_4b_5 \\ b_5b_1 & b_5b_2 & b_5b_3 & b_5b_4 & b_5^2+\sigma_{\symbf{\varepsilon}_5}^2 \\ \end{bmatrix} \\ &= \begin{bmatrix} b_1^2 & b_1b_2 & b_1b_3 & b_1b_4 & b_1b_5 \\ b_2b_1 & b_2^2 & b_2b_3 & b_2b_4 & b_2b_5 \\ b_3b_1 & b_3b_2 & b_3^2 & b_3b_4 & b_3b_5 \\ b_4b_1 & b_4b_2 & b_4b_3 & b_4^2 & b_4b_5 \\ b_5b_1 & b_5b_2 & b_5b_3 & b_5b_4 & b_5^2 \\ \end{bmatrix} + \begin{bmatrix} \sigma_{\symbf{\varepsilon}_1}^2 & 0 & 0 & 0 & 0 \\ 0 & \sigma_{\symbf{\varepsilon}_2}^2 & 0 & 0 & 0 \\ 0 & 0 & \sigma_{\symbf{\varepsilon}_3}^2 & 0 & 0 \\ 0 & 0 & 0 & \sigma_{\symbf{\varepsilon}_4}^2 & 0 \\ 0 & 0 & 0 & 0 & \sigma_{\symbf{\varepsilon}_5}^2 \\ \end{bmatrix} \\ &= \begin{bmatrix} b_1 \\ b_2 \\ b_3 \\ b_4 \\ b_5 \end{bmatrix}\begin{bmatrix} b_1 & b_2 & b_3 & b_4 & b_5 \end{bmatrix} + \symbf{\Psi} \\ &= \symbf{b}^\top\symbf{b} + \symbf{\Psi} \end{split} \end{aligned} \qquad(6.12)$ あとは $\symbf{\Sigma}$ とのズレがなるべく小さくなるような $\symbf{b},\symbf{\Psi}$ の値を計算していけばよいわけです。

なお $\symbf{\Psi}$ は観測変数の誤差分散を対角成分にもつ対角行列です。正確には $\symbf{\Psi}$ は独自因子間の相関行列（あるいは誤差共分散行列）なわけですが，上述の仮定のもとでは，誤差共分散＝非対角成分はゼロとなることを期待した上で，パラメータを推定していくのです。言い換えると，観測変数間の相関関係のうち，共通因子（ $\symbf{b}^{\top}\symbf{b}$ ）では説明できない部分が大きいと，上述の計算ではまともに観測変数の因子構造を正確に表現することはできないのです。

この「共通因子（ $\symbf{b}^{\top}\symbf{b}$ ）では説明できない部分」の大きさを考えるために，改めて(6.11)式について見てみます。この式の左辺の $\sigma_{\symbf{y}_i}^2$ は， $\symbf{y}_i$ が標準化されているため1となります。つまり， $b_i^2$ と $\sigma_{\varepsilon_i}^2$ の和は1です。そして $b_i^2$ の部分は，観測変数の分散を1としたとき，そのうち共通因子で説明可能な分散の割合を表しており，これは共通性(communality)と呼ばれています。つまり共通性は因子負荷の二乗に合致します。 また，残りの $\sigma_{\varepsilon_i}^2$ の部分は共通因子では説明できない（＝独自因子で説明可能な）分散の割合であり，これは独自性(uniqueness)と呼ばれています。つまり（当然ですが）共通性と独自性の和は必ず1になります。 また，共通性は，回帰分析における決定係数 $R^2$ （結果変数 $y$ の分散のうち説明変数で説明可能な分散の割合）に相当するものです。

あとはどうにかして因子負荷 $\symbf{b}$ および誤差分散 $\symbf{\Psi}$ が計算できたら，次はこれらを固定した上で， $\symbf{y}$ とのズレが最も小さくなるように因子得点 $\symbf{f}$ の値を計算する，というのが一般的な手順です。因子分析のような潜在変数モデルでは，多くの場合因子得点と因子負荷を同時に推定するのはかなり大変なので，このように先に項目パラメータを確定させてから回答者の特性値パラメータを推定する，という2段階の手続きをとります。

6.4.2 多因子の場合

因子の数が増えても，基本的には同じような形で観測変数の相関行列 $\symbf{\Sigma}$ を分解していくことになります。ちょっと長くなりますが，2因子モデルでの2項目の共分散＝相関係数を展開してみましょう。異なる項目の共通因子成分 $b_{ti}\symbf{f}_{t}$ と誤差成分 $\varepsilon_j$ が無相関，かつ独自因子間の相関も共通因子間の相関もゼロ⁷，すなわち $\begin{aligned} \begin{split} \sigma_{(b_{ti}\symbf{f}_{t}),(\symbf{\varepsilon}_j)} = \sigma_{(b_{tj}\symbf{f}_{t}),(\symbf{\varepsilon}_i)} &= 0 \\ \sigma_{(\symbf{\varepsilon}_i),(\symbf{\varepsilon}_j)} &= 0 \\ \sigma_{(b_{1i}\symbf{f}_{1}),(b_{2j}\symbf{f}_{2})} = \sigma_{(b_{2i}\symbf{f}_{2}),(b_{1j}\symbf{f}_{1})} &= 0 \end{split} \end{aligned} \qquad(6.13)$ だと仮定すると，項目 $\symbf{y}_i, \symbf{y}_j$ の共分散＝相関行列 $\symbf{\Sigma}$ の $(i,j)$ 成分は $\begin{aligned} \sigma_{\symbf{y}_i,\symbf{y}_j} &=&& r_{\symbf{y}_i,\symbf{y}_j}\\ &=&& \sigma_{(b_{1i}\symbf{f}_{1} + b_{2i}\symbf{f}_{2} + \symbf{\varepsilon}_i),(b_{1j}\symbf{f}_{1} + b_{2j}\symbf{f}_{2} + \symbf{\varepsilon}_j)} \\ &=&& \sigma_{(b_{1i}\symbf{f}_{1}),(b_{1j}\symbf{f}_{1})} + \sigma_{(b_{1i}\symbf{f}_{1}),(b_{2j}\symbf{f}_{2})} + \overbrace{\sigma_{(b_{1i}\symbf{f}_{1}),(\symbf{\varepsilon}_j)}}^{0} \\ &&+& \overbrace{\sigma_{(b_{2i}\symbf{f}_{2}),(b_{1j}\symbf{f}_{1})} + \sigma_{(b_{2i}\symbf{f}_{2}),(b_{2j}\symbf{f}_{2})} + \sigma_{(b_{2i}\symbf{f}_{2}),(\symbf{\varepsilon}_j)}}^{0} \\ &&+& \overbrace{\sigma_{(\symbf{\varepsilon}_i),(b_{1j}\symbf{f}_{1})} + \sigma_{(\symbf{\varepsilon}_i),(b_{2j}\symbf{f}_{2})} + \sigma_{(\symbf{\varepsilon}_i),(\symbf{\varepsilon}_j)}}^{0}\\ &=&& b_{1i}b_{1j}\sigma_{\symbf{f}_1}^2 + b_{2i}b_{2j}\sigma_{\symbf{f}_2}^2 \\ &=&& b_{1i}b_{1j} + b_{2i}b_{2j} \\ &=&& \begin{bmatrix} b_{1i} & b_{2i} \end{bmatrix}\begin{bmatrix} b_{1j} \\ b_{2j} \end{bmatrix} \\ &=&& \symbf{b}_i^{\top} \symbf{b}_j \end{aligned} \qquad(6.14)$ となります。同様にして，項目 $\symbf{y}_i$ の分散＝ $\symbf{\Sigma}$ の $(i,i)$ 成分は $\begin{aligned} \begin{split} \sigma_{\symbf{y}_i,\symbf{y}_i} &= b_{1i}^2 + b_{2i}^2 + \sigma_{\symbf{\varepsilon}_i}^2 \\ &= \begin{bmatrix} b_{1i} & b_{2i} \end{bmatrix}\begin{bmatrix} b_{1i} \\ b_{2i} \end{bmatrix} + \sigma_{\symbf{\varepsilon}_i}^2 \\ &= \symbf{b}_i^{\top} \symbf{b}_i + \sigma_{\symbf{\varepsilon}_i}^2 \end{split} \end{aligned} \qquad(6.15)$ となります。ここから，多因子の場合でも共通性は因子負荷の二乗（和）に合致するということがわかります。

あとはこれを複数の項目・因子に拡張するだけです。各項目の因子負荷ベクトルを横に並べていけば，全項目での全因子の負荷行列は $\begin{aligned} \begin{split} \symbf{B} &= \begin{bmatrix} \symbf{b}_1 & \symbf{b}_2 & \cdots & \symbf{b}_I \end{bmatrix} \\ &=\begin{bmatrix} b_{11} & b_{12} & \cdots & b_{1I} \\ b_{21} & b_{22} & \cdots & b_{2I} \\ \vdots & \vdots & \ddots & \vdots \\ b_{T-1,1} & b_{T-1,2} & \cdots & b_{T-1,I} \\ b_{T,1} & b_{T,2} & \cdots & b_{T,I} \\ \end{bmatrix} \end{split} \end{aligned} \qquad(6.16)$ となります。すると観測変数の相関行列 $\symbf{\Sigma}$ は結局 $\begin{aligned} \begin{split} \symbf{\Sigma} &= \symbf{B}^\top\symbf{B} + \symbf{\Psi} \\ &= \begin{bmatrix} \symbf{b}_1^\top \\ \symbf{b}_2^\top \\ \vdots \\ \symbf{b}_I^\top \end{bmatrix}\begin{bmatrix} \symbf{b}_1 & \symbf{b}_2 & \cdots & \symbf{b}_I \end{bmatrix} + \symbf{\Psi} \\ &= \begin{bmatrix} \symbf{b}_1^\top\symbf{b}_1 & \symbf{b}_1^\top\symbf{b}_2 & \cdots & \symbf{b}_1^\top\symbf{b}_I \\ \symbf{b}_2^\top\symbf{b}_1 & \symbf{b}_2^\top\symbf{b}_2 & \cdots & \symbf{b}_2^\top\symbf{b}_I \\ \vdots & \vdots & \ddots & \vdots \\ \symbf{b}_I^\top\symbf{b}_1 & \symbf{b}_I^\top\symbf{b}_2 & \cdots & \symbf{b}_I^\top\symbf{b}_I \end{bmatrix} + \symbf{\Psi} \end{split} \end{aligned} \qquad(6.17)$ と分解でき，あとは1因子のときと同じように $\symbf{B},\symbf{\Psi}$ を推定するだけです。

6.4.3 Rで確認してみる

以上のことを踏まえると，fa()関数で出力された因子負荷量は，実際の観測変数の相関行列と近い値になっていると期待されます。ということで見てみましょう。

まず，fa()関数に投入した10項目の相関行列は以下の方法で計算できました。

コード 6.6: 10項目の項目間相関

# round()関数を使って表示桁数を減らしています
Sigma_data <- cor(dat[, paste0("Q1_", 1:10)])
round(Sigma_data, 2)

       Q1_1 Q1_2 Q1_3 Q1_4 Q1_5  Q1_6  Q1_7 Q1_8 Q1_9 Q1_10
Q1_1   1.00 0.35 0.27 0.16 0.19 -0.01 -0.01 0.02 0.12  0.04
Q1_2   0.35 1.00 0.50 0.35 0.39  0.10  0.12 0.19 0.15  0.13
Q1_3   0.27 0.50 1.00 0.38 0.51  0.11  0.14 0.13 0.13  0.16
Q1_4   0.16 0.35 0.38 1.00 0.32  0.09  0.22 0.13 0.17  0.25
Q1_5   0.19 0.39 0.51 0.32 1.00  0.13  0.11 0.13 0.13  0.17
Q1_6  -0.01 0.10 0.11 0.09 0.13  1.00  0.43 0.31 0.37  0.27
Q1_7  -0.01 0.12 0.14 0.22 0.11  0.43  1.00 0.36 0.40  0.31
Q1_8   0.02 0.19 0.13 0.13 0.13  0.31  0.36 1.00 0.36  0.36
Q1_9   0.12 0.15 0.13 0.17 0.13  0.37  0.40 0.36 1.00  0.49
Q1_10  0.04 0.13 0.16 0.25 0.17  0.27  0.31 0.36 0.49  1.00

また，fa()関数で推定された因子負荷行列をもとに $\symbf{B}^\top\symbf{B}$ を計算すると，以下のようになります。

コード 6.7: 因子負荷行列から相関行列を復元

# 共通因子による部分
B <- res_fa$loadings
cor_B <- B %*% t(B)
# 独自因子の部分
Psi <- diag(res_fa$uniquenesses)
# 和を取る
Sigma_model <- cor_B + Psi
round(Sigma_model, 2)

       Q1_1  Q1_2  Q1_3 Q1_4  Q1_5  Q1_6  Q1_7  Q1_8  Q1_9 Q1_10
Q1_1   1.02  0.29  0.32 0.18  0.25 -0.07 -0.06 -0.04 -0.05 -0.02
Q1_2   0.29  1.00  0.53 0.32  0.41 -0.03 -0.01  0.02  0.00  0.04
Q1_3   0.32  0.53  1.01 0.35  0.47 -0.05 -0.03  0.00 -0.02  0.03
Q1_4   0.18  0.32  0.35 0.96  0.28  0.06  0.08  0.09  0.10  0.11
Q1_5   0.25  0.41  0.47 0.28  0.99 -0.01  0.01  0.03  0.02  0.05
Q1_6  -0.07 -0.03 -0.05 0.06 -0.01  1.02  0.37  0.32  0.39  0.33
Q1_7  -0.06 -0.01 -0.03 0.08  0.01  0.37  1.01  0.35  0.43  0.37
Q1_8  -0.04  0.02  0.00 0.09  0.03  0.32  0.35  0.99  0.38  0.32
Q1_9  -0.05  0.00 -0.02 0.10  0.02  0.39  0.43  0.38  1.00  0.39
Q1_10 -0.02  0.04  0.03 0.11  0.05  0.33  0.37  0.32  0.39  0.98

なお，cor_Bの計算において $\symbf{B}^\top\symbf{B}$ ではなく転置行列が後ろに来ていますが，これは(6.16)式での $\symbf{B}$ の定義から見ると，fa()関数が出力する因子負荷行列がちょうど $\symbf{B}^\top$ にあたる形になっているためです。したがって，計算自体は $\symbf{B}^\top\symbf{B}$ を行っています。

観測変数の相関行列Sigma_dataと，モデルパラメータ（推定値）で復元された相関行列Sigma_modelのズレを見るために，差を取ってみると，以下のようになります。

コード 6.8: 相関行列の差

round(Sigma_model - Sigma_data, 2)

       Q1_1  Q1_2  Q1_3  Q1_4  Q1_5  Q1_6  Q1_7  Q1_8  Q1_9 Q1_10
Q1_1   0.02 -0.07  0.05  0.02  0.06 -0.05 -0.05 -0.06 -0.17 -0.06
Q1_2  -0.07  0.00  0.03 -0.03  0.02 -0.13 -0.13 -0.17 -0.15 -0.09
Q1_3   0.05  0.03  0.01 -0.03 -0.05 -0.16 -0.17 -0.12 -0.14 -0.13
Q1_4   0.02 -0.03 -0.03 -0.04 -0.04 -0.03 -0.14 -0.04 -0.08 -0.14
Q1_5   0.06  0.02 -0.05 -0.04 -0.01 -0.14 -0.11 -0.10 -0.11 -0.12
Q1_6  -0.05 -0.13 -0.16 -0.03 -0.14  0.02 -0.07  0.00  0.02  0.06
Q1_7  -0.05 -0.13 -0.17 -0.14 -0.11 -0.07  0.01 -0.01  0.03  0.06
Q1_8  -0.06 -0.17 -0.12 -0.04 -0.10  0.00 -0.01 -0.01  0.01 -0.04
Q1_9  -0.17 -0.15 -0.14 -0.08 -0.11  0.02  0.03  0.01  0.00 -0.10
Q1_10 -0.06 -0.09 -0.13 -0.14 -0.12  0.06  0.06 -0.04 -0.10 -0.02

結果が一致しないのは当然のことです。観測変数間の相関は全部で ${}_10 C_{2}=45$ 個ある一方で，モデルパラメータは因子負荷が $10\times2=20$ 個しかないためです。ただしズレは，最大で0.17（Q1_3とQ1_7）となっており，また0.1以下に収まっているペアも少なくないので，（どう感じるかは人それぞれですが）大ハズシとも言えないくらいの感じに収まっているようにも見えます。

因子分析は，モデル上ではいま示したように $\symbf{B}^\top\symbf{B} + \symbf{\Psi}$ が $\symbf{\Sigma}$ と近づくように推定を行います。そして $\symbf{B}^\top\symbf{B} + \symbf{\Psi}$ と $\symbf{\Sigma}$ のズレは，図 6.9 に示したような「共通因子では説明できない相関関係」を意味しています。したがって，あまりにズレが大きい場合には，まだ他に共通因子が存在している可能性もあります。

6.5 因子負荷の推定法の実際

因子分析も回帰分析モデルと同じように，共通因子の成分 $\symbf{F}\symbf{b}_{i}$ によって回答 $\symbf{y}$ を予測（あるいは近似）することが目的です。回帰分析では決定係数が高いほど予測の精度が良かったように，因子分析でも共通性の割合が高いほうが基本的には嬉しいものです。当然ながら，共通性の割合は共通因子の数が増えるほど高くなるわけですが，fa()関数に引数nfactorsが用意されていたように，因子分析では共通因子の数は分析者が自由に設定できます。とはいえ本当にいくつでも良いわけではなく，因子分析の目的からすると「観測変数を適当な数のグループに分けたい」はずです。その「適当な数」を求める際には，例えば回帰分析における変数選択（決定係数があまり上がらない説明変数は入れないようにする）と同じ要領で，共通性が大きく増加しないような共通因子は入れないようにしようなどといったことが言えそうです。

ここで，因子分析における「共通因子の数」の意味を理解するために，実際にどのように因子負荷行列を計算しているかを紹介します。これに基づいて実際に因子数を決めるための方法に関しては Section 6.11 にて紹介します。なお本Sectionで紹介するものは，因子分析におけるパラメータ推定法の一種である主因子法と呼ばれる方法です。他にも因子負荷行列を推定する方法はある（ Section 6.10 を参照）のですが，観測変数間の相関関係の説明の分かりやすさから，主因子法に基づいて説明をしていきます。

因子分析で因子負荷行列を求めるという行為は，観測変数間の $I\times I$ 相関行列 $\symbf{\Sigma}$ から，(6.16)式に示されている $T\times I$ の行列 $\symbf{B}$ を得る，ということです。そのために使われるのが，固有値分解と呼ばれる行列の変換方法です。細かいことは省略しますが，固有値分解とは対称行列（ここでは $I\times I$ 相関行列 $\symbf{\Sigma}$ ）を $\symbf{\Sigma} = \symbf{X\Lambda X}^\top \qquad(6.18)$ という要素に分解する操作のことです。ここで， $\symbf{X}$ は $I$ 本の線形独立な長さ $I$ の縦ベクトル（固有ベクトル）が横に並んだ形 $\begin{aligned} \symbf{X} = \begin{bmatrix} \symbf{x}_1 & \symbf{x}_2 & \cdots & \symbf{x}_I \end{bmatrix} = \begin{bmatrix} x_{11} & x_{12} & \cdots & x_{1I} \\ x_{21} & x_{22} & \cdots & x_{2I} \\ \vdots & \vdots & \ddots & \vdots \\ x_{I1} & x_{I2} & \cdots & x_{II} \end{bmatrix} \end{aligned} \qquad(6.19)$ をしています。つまり $I\times I$ の行列です。

また， $\symbf{\Lambda}$ は固有値 $\begin{pmatrix}\lambda_1, & \lambda_2, & \cdots, & \lambda_I\end{pmatrix}$ を対角成分にもつ対角行列 $\begin{aligned} \begin{split} \symbf{\Lambda} = \begin{bmatrix} \lambda_1 & 0 & \cdots & 0 \\ 0 & \lambda_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \lambda_I \\ \end{bmatrix} \end{split} \end{aligned} \qquad(6.20)$ になっています。

Rではeigen()という関数で固有値分解を行うことができるので，実際に行列を分解→復元してみましょう。

コード 6.9: 行列を固有値分解

# Q1_1からQ1_5の相関行列で試してみます
eig <- eigen(cor(dat[, 2:6]))
eig$values # 固有値

[1] 2.4143113 0.8819440 0.6987614 0.5517027 0.4532806

eig$vectors # 固有ベクトル

           [,1]       [,2]         [,3]       [,4]        [,5]
[1,] -0.3333328  0.8503498 -0.132707026 -0.3843622 -0.02118902
[2,] -0.4936057  0.1622930  0.002823959  0.7651945  0.38011021
[3,] -0.5164665 -0.1419179  0.239729691  0.0954805 -0.80407389
[4,] -0.4058417 -0.3777438 -0.802813913 -0.2100389  0.06305300
[5,] -0.4623825 -0.2962012  0.529528437 -0.4620716  0.45227951

ここで，固有ベクトルに関してはそれぞれ要素の二乗和が1，つまり $\sum_{i=1}^I x_{ij}^2 = \symbf{x}_j^\top\symbf{x}_j = 1 \; \forall j \qquad(6.21)$ となるように標準化された値が算出されています。

コード 6.10: 固有値分解からもとの行列を復元

# 復元した値
eig$vectors %*% diag(eig$values) %*% t(eig$vectors)
# もとの（相関）行列
cor(dat[, 2:6])

          [,1]      [,2]      [,3]      [,4]      [,5]
[1,] 1.0000000 0.3527771 0.2744489 0.1616950 0.1945084
[2,] 0.3527771 1.0000000 0.4974111 0.3501907 0.3925362
[3,] 0.2744489 0.4974111 1.0000000 0.3848005 0.5131434
[4,] 0.1616950 0.3501907 0.3848005 1.0000000 0.3211529
[5,] 0.1945084 0.3925362 0.5131434 0.3211529 1.0000000
          Q1_1      Q1_2      Q1_3      Q1_4      Q1_5
Q1_1 1.0000000 0.3527771 0.2744489 0.1616950 0.1945084
Q1_2 0.3527771 1.0000000 0.4974111 0.3501907 0.3925362
Q1_3 0.2744489 0.4974111 1.0000000 0.3848005 0.5131434
Q1_4 0.1616950 0.3501907 0.3848005 1.0000000 0.3211529
Q1_5 0.1945084 0.3925362 0.5131434 0.3211529 1.0000000

確かに完全に一致しています。

これだけだと何をやっているかまだよく分からないと思いますが，とりあえず固有値分解の結果をそのまま因子負荷行列 $\symbf{B}$ として使っていくことにしましょう。 (6.17)式では， $\symbf{\Sigma}$ を「共通因子に起因する成分」 $\symbf{B^\top B}$ と「独自因子に起因する成分」 $\symbf{\Psi}$ に分解していました。このうち $\symbf{B^\top B}$ の部分を固有値分解によって求めるならば， $\symbf{B}=\sqrt{\symbf{\Lambda}}\symbf{X}^{\top}$ としたら良さそうです。こうして求められた因子負荷行列 $\symbf{B}$ は，もとの観測変数間の相関行列 $\symbf{\Sigma}$ の非対角成分，つまり相関関係については完全に復元できる因子負荷行列になっています（ $\symbf{\Psi}$ を無視しているので対角成分は復元できない）。ちなみに図で表すと，因子負荷行列 $\symbf{B}$ の因子数が項目数と同じ（ $T=I$ ）ということなので，例えば5項目ならば図 6.10 のような状態です。

ここでは固有値分解の意味までは踏み込みません。とりあえず固有値分解を使えば行列をベクトル（とスカラー）に分解できるということ，そして項目数と同じ数の共通因子があれば，観測変数間の相関関係を完全に表現できるということを理解しておいてください。

ただ，因子分析の目的は「複数の観測変数の背後にある少数の共通因子を見つけ出したい」なので，その目的からすると図 6.10 のように「項目数と同じ数の共通因子」があっても何も嬉しくないですね。ここからどうにかして図 6.3 や図 6.5 のように項目数よりもできるだけ少ない数の共通因子によって，観測変数間の相関構造をできるだけ正確に表現したいものです。

ということで，固有値分解の性質を更に深掘りしていきます。固有値分解の式を， $\symbf{\Lambda}$ の対角成分の要素（固有値）ごとに分けて見てみると， $\begin{aligned} \symbf{\Sigma} &= \symbf{X}\symbf{\Lambda}\symbf{X}^\top\\ &= \lambda_1\symbf{x}_1\symbf{x}_1^\top + \lambda_2\symbf{x}_2\symbf{x}_2^\top + \cdots + \lambda_I\symbf{x}_I\symbf{x}_I^\top \end{aligned} \qquad(6.22)$ という形に展開することができます。つまり各固有ベクトルに，対応する固有値をかけたものの和になっているということです。そして固有値分解の嬉しい性質として，固有値の大きいところだけを使った近似ができるという点があります。例えば上の式に関して，固有値の一番大きい $\lambda_1$ に関するところだけを使った $\begin{aligned} \symbf{\Sigma} &\cong \lambda_1\symbf{x}_1\symbf{x}_1^\top \\ & = 2.414\begin{bmatrix} -0.333 \\ -0.494 \\ -0.516 \\ -0.406 \\ -0.462 \end{bmatrix}\begin{bmatrix} -0.333 & -0.494 & -0.516 & -0.406 & -0.462 \end{bmatrix} \\ &= \begin{bmatrix} 0.268 & 0.397 & 0.416 & 0.327 & 0.372 \\ 0.397 & 0.588 & 0.615 & 0.484 & 0.551 \\ 0.416 & 0.615 & 0.644 & 0.506 & 0.577 \\ 0.327 & 0.484 & 0.506 & 0.398 & 0.453 \\ 0.372 & 0.551 & 0.577 & 0.453 & 0.516 \end{bmatrix} \end{aligned} \qquad(6.23)$

は，単一のベクトルと定数による近似の中では最も良い近似になっている⁸のです。つまり，もしも共通因子を1個だけにしたい場合には，固有値分解で得られた $\sqrt{\lambda_1}\symbf{x}_1^\top$ を因子負荷ベクトル $\symbf{b}$ とすることで， $\symbf{b}^\top\symbf{b} = \lambda_1\symbf{x}_1\symbf{x}_1^\top$ が共通因子が1個だけという条件の中では観測変数の相関行列 $\symbf{\Sigma}$ を最も良く近似できる因子負荷ベクトルになることが分かる，というのが固有値分解のすごいところです。

同様に， $\symbf{\Sigma} \cong \lambda_1\symbf{x}_1\symbf{x}_1^\top + \lambda_2\symbf{x}_2\symbf{x}_2^\top \qquad(6.24)$ は2つのベクトルを使った近似の中では最も良い近似になっており，因子1,2に関する因子負荷の横ベクトルをそれぞれ $\symbf{b}_1, \symbf{b}_2$ とおけば， $\begin{aligned} \begin{split} \symbf{B}^\top\symbf{B} &= \begin{bmatrix} \symbf{b}_1^\top & \symbf{b}_2^\top \end{bmatrix}\begin{bmatrix} \symbf{b}_1 \\ \symbf{b}_2 \end{bmatrix}\\ &= \begin{bmatrix} \symbf{x}_1 & \symbf{x}_2 \end{bmatrix} \begin{bmatrix} \lambda_1 & 0 \\ 0 & \lambda_2 \end{bmatrix} \begin{bmatrix} \symbf{x}_1^\top \\ \symbf{x}_2^\top \end{bmatrix} \\ &= \begin{bmatrix} \sqrt{\lambda_1}\symbf{x}_1 & \sqrt{\lambda_2}\symbf{x}_2 \end{bmatrix}\begin{bmatrix} \sqrt{\lambda_1}\symbf{x}_1^\top \\ \sqrt{\lambda_2}\symbf{x}_2^\top \end{bmatrix} \end{split} \end{aligned} \qquad(6.25)$ という形で，因子の数がいくつであっても一因子のときと同様に，相関行列を最も良く近似できる因子負荷行列 $\symbf{B}$ を求めることができるわけです。

ここまでの議論からは

因子の数は最大でも $I$ 個である（固有値分解するため）
因子の数が増えるほどデータの相関行列をより良く近似できる
固有ベクトルはすべて標準化（ $\symbf{x}_i^\top\symbf{x}_i=1$ ）されており固有値は大きい順に並んでいるため，1個目の因子が一番強い

といったことがわかります。

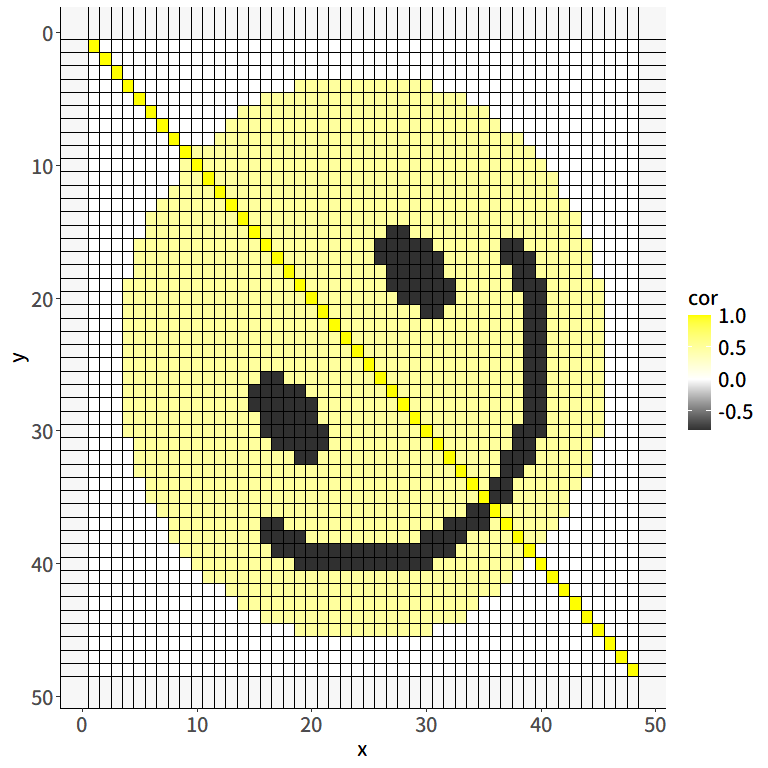
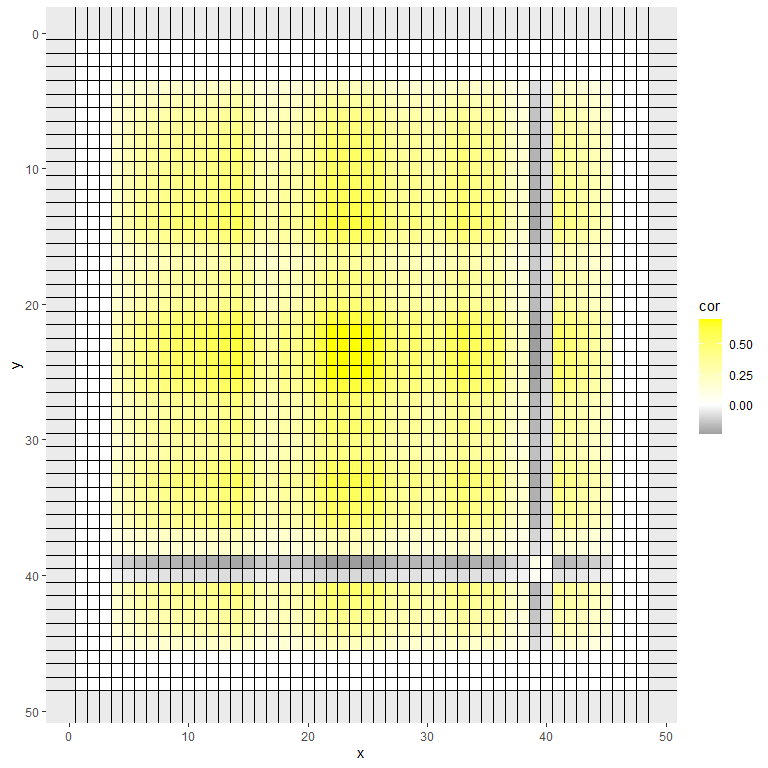
ではここで，固有ベクトルによる相関行列の近似のイメージを掴むための例を見てみます⁹。以下の図 6.11 は，（仮想的な）48項目の相関行列をヒートマップに落とし込んだものです。無相関のところを白色として，黄色が濃いほど正の相関が強く，黒が濃いほど負の相関が強い場所を表すように色をつけたところ，偶然ニッコリ笑顔にみえるような相関行列が得られたとします。

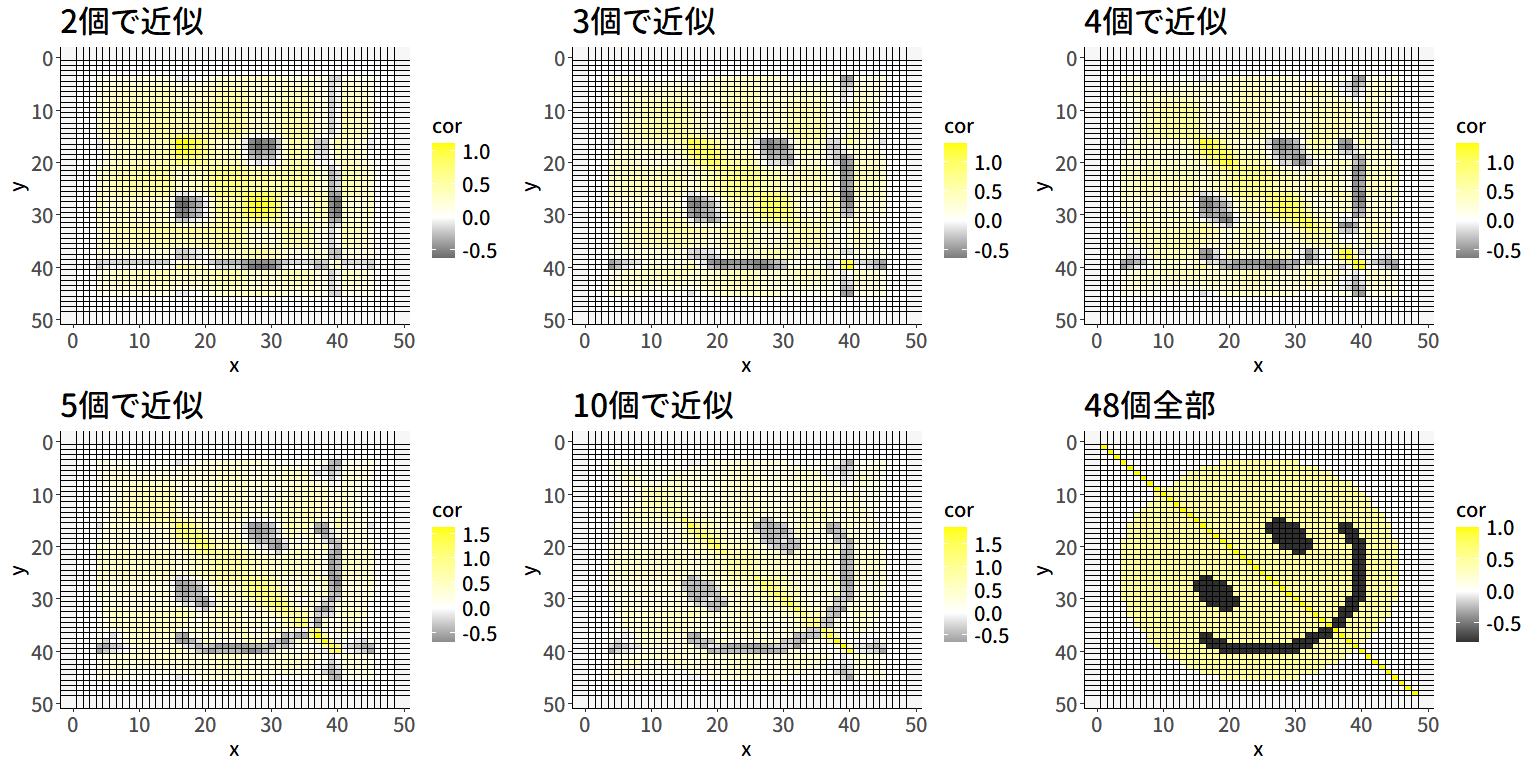
では，この相関行列を固有値分解して，最初の固有ベクトルのみを使った近似 $\lambda_1\symbf{x}_1\symbf{x}_1^\top$ を見てみましょう。うまく近似できたら図 6.11 のようなニッコリ笑顔になっているはずですが，図 6.12 にはその面影は全くありません…。最初の固有ベクトル1個だけを使った近似は，因子分析で言えばすべての項目が概ね単一の共通因子のみの影響を受けている状態（図 6.3）を考えているわけですが，図 6.11 の相関行列では負の相関を持つ（黒く塗りつぶされた）ペアもそれなりに存在しているため，一因子ではさすがに無理がある，ということを表しています。

ということで，もう少し多くの固有ベクトルを使って近似してみましょう。図 6.13 ではそれぞれc(2:5, 10, 48)個の固有ベクトルを使った近似に基づくヒートマップが描かれています。当然48個全てを使えば完璧な復元ができる（6.18式）わけですが，この図を見ると大体5個くらいでもニッコリ笑顔の感じは割と復元されているように見えます。固有値分解を用いることで，本来の変数の数（この例では48）よりもかなり少ない数（この例では5-10くらい）の共通因子があれば，もとの相関行列の大体の感じを説明可能となります。これこそが因子分析が目指している「なるべく少ない共通因子で説明する」の本質なのです。つまり因子分析では，観測された $I\times I$ 相関行列 $\symbf{\Sigma}$ を固有値分解し，そのうち $T~(T<I)$ 個の固有値と固有ベクトルを使って，相関行列を $\begin{aligned} \begin{split} \symbf{\Sigma} &\cong \lambda_1\symbf{x}_1\symbf{x}_1^\top + \lambda_2\symbf{x}_2\symbf{x}_2^\top + \cdots +\lambda_T\symbf{x}_T\symbf{x}_T^\top \\ & = \sum_{t=1}^{T}\lambda_t\symbf{x}_t\symbf{x}_t^\top \end{split} \end{aligned} \qquad(6.26)$ という形で近似しているのです。

ちなみに，すべて項目の因子負荷の二乗和を固有値分解的に表すと， $\begin{aligned} \begin{split} \mathrm{tr}(\symbf{B}^\top\symbf{B}) &= \sum_{t=1}^T\sum_{i=1}^I \lambda_t x_{it}^2 \\ &= \sum_{t=1}^T\lambda_t \sum_{i=1}^I x_{it}^2 \end{split} \end{aligned} \qquad(6.27)$ という形になります。固有値分解で得られる固有ベクトルは標準化されているため， $\sum_{i=1}^I x_{it}^2 = 1 \; \forall t \qquad(6.28)$ となっています。したがって， $\mathrm{tr}(\symbf{B}^\top\symbf{B}) = \sum_{t=1}^T \lambda_t \qquad(6.29)$ となります。これは，固有値こそが因子負荷の合計を決めており，ひいては分散説明率（共通性）の合計を規定していることを表しています。ここからも，共通因子の数を決める際に何を意識したら良いかが見えてきます。

相関構造が複雑な場合，共通因子の数が少なすぎるとデータへの当てはまりが悪くなるので良くない
因子の数が増えるほど分散説明率が増える＝共通性の値が大きくなる
後ろの固有値になるほど影響が小さくなるので，無くても良くなってくる

実際にどういった指標を用いて因子数を決めたら良いかは Section 6.11 までお待ち下さい。

先ほどfa()によって得られた因子負荷はかなり単純構造に近かったわけですが，いま説明したように，固有値分解によって因子負荷を推定すると解は一つ（ $\symbf{b}_t = \sqrt{\lambda_t}\symbf{x}_t$ ）に決まります。そして第1因子については，全ての因子負荷に最も大きい固有値（ $\lambda_1$ ）がかかっているわけなので，基本的に1つ目の共通因子は全ての項目に対して高い因子負荷となりがちです。このままでは，1つ目の共通因子は常に「総合的な何か」としか解釈できなくなってしまいそうです。

ただ実際にはそんなことはありません。これには因子分析の解の不定性が大きく関係しています。

6.5.1 因子の回転

まずは因子分析における解の不定性を数理的に説明していきます。

(6.7)式では，単一の項目 $i$ に関する因子分析モデルを，回帰分析と同様に $\begin{aligned} \begin{split} \symbf{y}_i &= \symbf{f}_1b_{1i} + \symbf{f}_2b_{2i} + \cdots + \symbf{f}_Tb_{Ti} + \symbf{\varepsilon}_i \\ &= \begin{bmatrix} \symbf{f}_1 & \symbf{f}_2 & \cdots & \symbf{f}_T \end{bmatrix} \begin{bmatrix} b_{1i} \\ b_{2i} \\ \vdots \\ b_{Ti} \end{bmatrix} + \symbf{\varepsilon}_i \\ &= \symbf{F}\symbf{b}_i + \symbf{\varepsilon}_i \end{split} \qquad{(6.7)} \end{aligned}$ と表現しました。これを全項目についてまとめて線形代数で表すと，以下のようになります。 $\begin{aligned} \begin{split} \symbf{Y} &= \begin{bmatrix} \symbf{y}_1 & \symbf{y}_2 & \cdots & \symbf{y}_I \end{bmatrix} \\ &= \begin{bmatrix} f_{11} & f_{12} & \cdots & f_{1T} \\ f_{21} & f_{22} & \cdots & f_{2T} \\ \vdots & \vdots & \ddots & \vdots \\ f_{P1} & f_{P2} & \cdots & f_{PT} \end{bmatrix} \begin{bmatrix} b_{11} & b_{12} &\cdots & b_{1I} \\ b_{21} & b_{22} &\cdots & b_{2I} \\ \vdots & \vdots & \ddots & \vdots \\ b_{T1} & b_{T2} &\cdots & b_{TI} \end{bmatrix} + \begin{bmatrix} \varepsilon_{11} & \varepsilon_{12} & \cdots & \varepsilon_{1I} \\ \varepsilon_{21} & \varepsilon_{22} & \cdots & \varepsilon_{2I} \\ \vdots & \vdots & \ddots & \vdots \\ \varepsilon_{P1} & \varepsilon_{P2} & \cdots & \varepsilon_{PI} \\ \end{bmatrix} \\ &= \symbf{FB} + \symbf{E} \end{split} \end{aligned} \qquad(6.30)$

表記がこんがらがってきたのでおさらいしておきますが，

因子得点 $f_{pt}$ にある2つの添字は回答者（ $P$ ）と因子（ $T$ ）
因子負荷 $b_{ti}$ にある2つの添字は因子（ $T$ ）と項目（ $I$ ）
残差 $\varepsilon_{pi}$ にある2つの添字は回答者（ $P$ ）と項目（ $I$ ）

です。ここで，共通因子に関する部分 $\symbf{FB}$ について次のような操作を考えてみます。

因子負荷行列 $\symbf{B}$ に対して，正則な（＝逆行列が存在する）対称行列 $\symbf{A}$ を左からかけたものを $\tilde{\symbf{B}}=\symbf{A}\symbf{B}$ とする
因子得点行列 $\symbf{F}$ に対して，その逆行列 $\symbf{A}^{-1}$ を右にかけたものを $\tilde{\symbf{F}}=\symbf{F}\symbf{A}^{-1}$ とする

すると， $\tilde{\symbf{F}}\tilde{\symbf{B}}=\symbf{F}\symbf{A}^{-1}\symbf{A}\symbf{B}=\symbf{FB}$ となります。そして正則な対称行列 $\symbf{A}$ というのは無限に存在しています。したがって，観測された相関行列 $\symbf{\Sigma}$ に対する当てはまりが同じになる因子得点 $\symbf{F}$ と因子負荷 $\symbf{B}$ の組み合わせが無限に存在しているわけです。そうだとすると，その中でどの組み合わせを最終的に使えばよいのでしょうか…

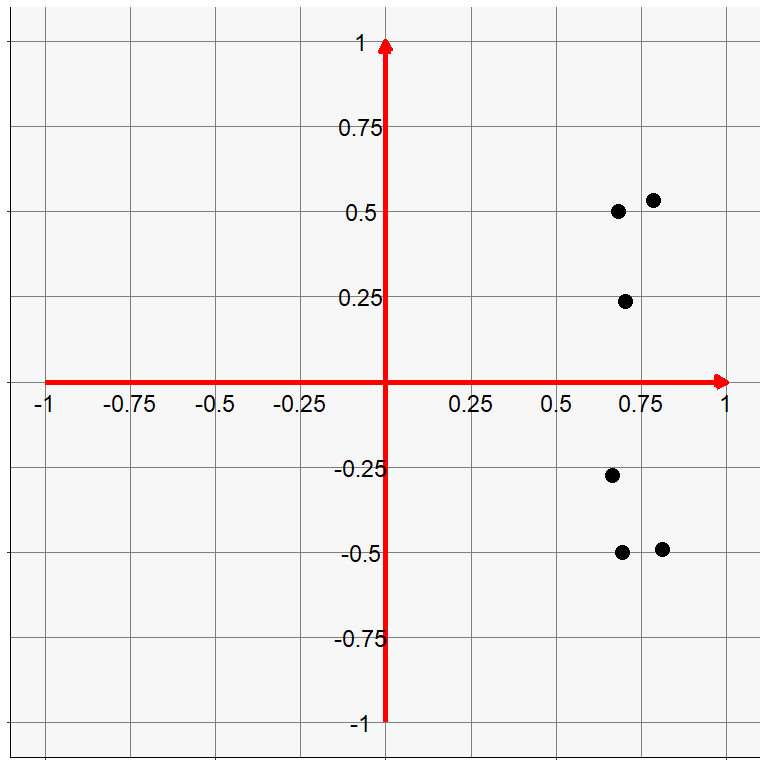
因子分析では，この不定性をむしろ利用して，都合の良い組み合わせを選んで使うということにしています。具体的に， $\symbf{FB}$ を自由に変換できると何が嬉しいのかを，もう少しイメージを交えて説明しましょう。ある6項目の相関行列に対して固有値分解を行い，得られた2つの因子に対する因子負荷量（表 6.3 ）を二次元にプロットしたものが図 6.14 です。どうやら3項目ずつのグループに分かれそうですね。ですがこのままでは全ての項目が因子1に対して高い負荷を持っているため，因子1は「総合的な何か」としか解釈できません。

表 6.3: 因子負荷行列(

\symbf{B}^\top

)

F1	F2
0.702	0.238
0.683	0.500
0.787	0.532
0.811	-0.492
0.694	-0.499
0.665	-0.273

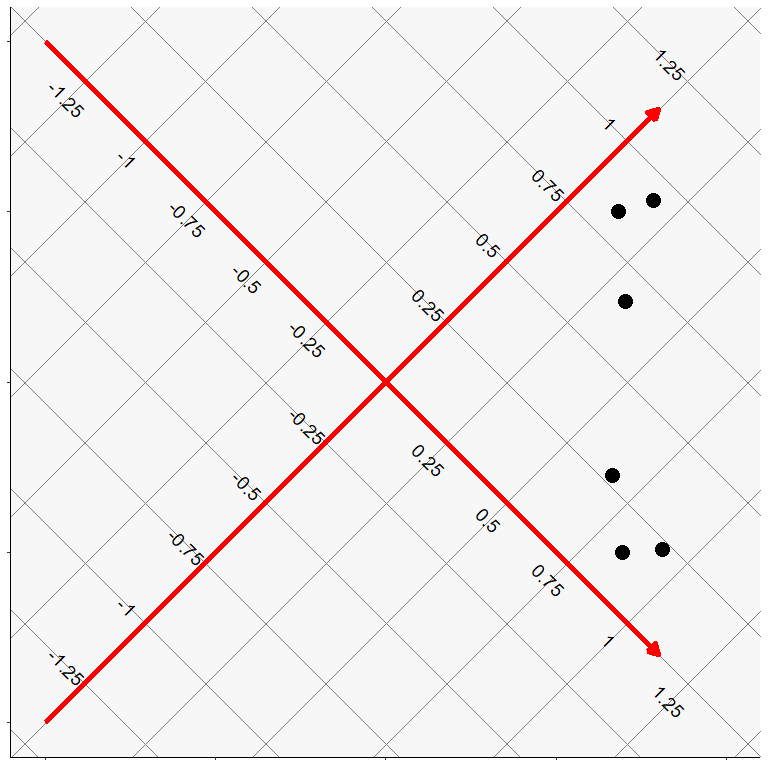
図 6.14 のようなプロットに対して，正則な対称行列 $\symbf{A}$ による変換は，プロットの軸を回転させることに相当します。例えば2次元の回転ならば， $\begin{aligned} \symbf{A}= \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} \end{aligned} \qquad(6.31)$ という行列を左からかけることは，原点を中心に時計回りに $\theta$ 度回転することに対応しています。また，この行列には逆行列 $\begin{aligned} \symbf{A}^{-1}= \begin{bmatrix} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \end{bmatrix} \end{aligned} \qquad(6.32)$ が存在しているため， $\tilde{\symbf{F}}=\symbf{F}\symbf{A}^{-1}$ の計算も可能です。試しに図 6.15 のように軸を時計回りに45度回転させると，図 6.14 よりは単純構造に近づけることができそうです。

実際に因子負荷行列を変換させてみると， $\begin{aligned} \symbf{A}\symbf{B} &= \begin{bmatrix} \cos45^{\circ} & -\sin45^{\circ} \\ \sin45^{\circ} & \cos45^{\circ} \end{bmatrix}\begin{bmatrix} 0.702 & 0.683 & 0.787 & 0.811 & 0.694 & 0.665 \\ 0.238 & 0.500 & 0.532 & -0.492 & -0.499 & -0.273 \end{bmatrix} \\ &= \begin{bmatrix} 0.707 & -0.707 \\ 0.707 & 0.707 \end{bmatrix} \begin{bmatrix} 0.702 & 0.683 & 0.787 & 0.811 & 0.694 & 0.665 \\ 0.238 & 0.500 & 0.532 & -0.492 & -0.499 & -0.273 \end{bmatrix} \\ &=\begin{bmatrix} 0.328 & 0.129 & 0.180 & \mathbf{0.921} & \mathbf{0.844} & \mathbf{0.663} \\ \mathbf{0.665} & \mathbf{0.836} & \mathbf{0.933} & 0.226 & 0.138 & 0.277 \end{bmatrix} \end{aligned}$ となり，表 6.3 よりはいい感じに3項目ずつに分かれました。

ここまでは，2つの軸が直角に交わった状態を保ちながら回転をさせてきました。このような回転のことを直交回転(orthogonal rotation)と呼びます。固有値分解で得られる（初期状態の）固有ベクトルは，互いに直交するようになっています。直交するということは，言い換えると相関がないということです。つまり，直交回転は因子間相関がゼロという制約のもとで単純構造を目指す回転なのです。ですが，ほとんどの場合ではわざわざ因子間相関をゼロに制約する必要はないでしょう。むしろ，因子の間には少なからず相関関係が見られるはずです。

2つの因子の相関係数は，2つの軸が作る角度 $\theta$ に対して $\cos\theta$ になります。直交回転では必ず相関が $\cos90^{\circ}=0$ になっているわけですが，もし2つの因子の軸が作る角度が $90^{\circ}$ 以外になっても良いならば，図 6.15 よりも更に良い単純構造が目指せそうです。実際に，例えば回転行列 $\symbf{A}$ を $\symbf{A}= \begin{bmatrix} 0.613 & -0.902 \\ 0.582 & 0.922 \end{bmatrix}$ と設定すると，変換後の因子負荷行列 $\tilde{\symbf{B}}$ は $\begin{aligned} \symbf{A}\symbf{B} &= \begin{bmatrix} 0.613 & -0.902 \\ 0.582 & 0.922 \end{bmatrix}\begin{bmatrix} 0.702 & 0.683 & 0.787 & 0.811 & 0.694 & 0.665 \\ 0.238 & 0.500 & 0.532 & -0.492 & -0.499 & -0.273 \end{bmatrix} \\ &=\begin{bmatrix} 0.216 & -0.032 & 0.002 & \mathbf{0.941} & \mathbf{0.876} & \mathbf{0.654} \\ \mathbf{0.628} & \mathbf{0.859} & \mathbf{0.949} & 0.018 & -0.057 & 0.135 \end{bmatrix} \end{aligned}$ となり，直交回転のときよりもさらに単純構造になりました。

図 6.16 のように，因子間の相関を認めながら回転を行うことを斜交回転(oblique rotation)と呼びます。なお，回転行列 $\symbf{A}$ によって初期解を回転させた時，因子得点行列 $\symbf{F}$ は $\tilde{\symbf{F}}=\symbf{F}\symbf{A}^{-1}$ と変換されているため，因子間相関行列 $\symbf{\Phi}$ は $(\symbf{A}\symbf{A}^\top)^{-1}$ によって求めることができます。例えば先程の数値例の場合は， $\begin{aligned} \symbf{\Phi} &= (\symbf{A}\symbf{A}^\top)^{-1} \\ &= \left(\begin{bmatrix} 0.613 & -0.902 \\ 0.582 & 0.922 \end{bmatrix}\begin{bmatrix} 0.613 & 0.582 \\ -0.902 & 0.922 \end{bmatrix}\right)^{-1} \\ &\simeq \begin{bmatrix} 1 & 0.400 \\ 0.400 & 1 \end{bmatrix} \end{aligned}$ となり，回転後の因子間相関は0.4と計算できます。 $\cos\theta=0.4$ ということは，図 6.16 の2軸が作る角度がおよそ $\theta=66.4$ 度になっている，ということです。

回転後の因子間相関の導出

あるデータ行列 $\symbf{X}$ は，各行が個人を，各列が変数を表している $P\times I$ の行列とします（datなどと同じ形式）。これに対する分散共分散行列 $\symbf{\Sigma}$ の $(s,t)$ 成分は変数 $s$ と変数 $t$ の共分散なので， $\begin{aligned} \sigma_{st}&=\frac{1}{P}\sum_{p=1}^{P}(x_{ps}-\bar{x_s})(x_{pt}-\bar{x_t}) \\ &=E\left[(x_{ps}-\bar{x_s})(x_{pt}-\bar{x_t})\right] \end{aligned}$ と単純に因子得点の積の期待値になります。ただし $\bar{x_s}$ は変数 $s$ の平均値です。

これを因子得点行列 $\symbf{F}$ に置き換えて考えてみると，因子分析では基本的な設定の一つとして，各行（各因子の因子得点）の平均値（ $\bar{x_s}$ や $\bar{x_t}$ に相当するもの）はそれぞれ0という制約を置いているため，因子 $s$ と因子 $t$ の共分散は $\begin{aligned} \sigma_{st}&=\frac{1}{P}\sum_{p=1}^{P}f_{ps}f_{pt} \\ &=E\left[f_{ps}f_{pt}\right] \end{aligned}$ となります。同様に，各列（因子得点）の標準偏差は1に制約されているため，分散共分散行列 $\symbf{\Sigma}$ はそのまま相関行列として見ることができます。

ということで因子得点の相関行列は，上の式を行列全体に拡張することで $E[\symbf{F}^\top\symbf{F}]$ と表すことができます。回転前の初期解（固有ベクトル同士）は必ず無相関なので， $E[\symbf{F}^\top\symbf{F}]=\symbf{I}$ ということです。 $\tilde{\symbf{F}}^\top=(\symbf{F}\symbf{A}^{-1})^\top={\symbf{A}^{-1}}^\top\symbf{F}^\top$ であることを利用すると，回転後の因子間相関は $\begin{aligned} E[\tilde{\symbf{F}}^\top\tilde{\symbf{F}}] &= E[{\symbf{A}^{-1}}^\top\symbf{F}^\top\symbf{F}\symbf{A}^{-1}] \\ &= {\symbf{A}^{-1}}^\top E[\symbf{F}^\top\symbf{F}]{\symbf{A}^{-1}} \\ &= {\symbf{A}^{-1}}^\top\symbf{I}{\symbf{A}^{-1}} \\ &= {\symbf{A}^{-1}}^\top{\symbf{A}^{-1}} \\ &= (\symbf{A}\symbf{A}^\top)^{-1} \end{aligned}$ となるわけです。

直交回転にせよ斜交回転にせよ，図 6.14 から図 6.16 における各項目のプロットの位置関係は変わりません。また，共通性と独自性の値も変わりません。回転の不定性を利用することによって，「相関行列から項目のグルーピングを行う」という基本姿勢は変わること無く，より解釈しやすいように因子負荷量をいい感じにしてあげるわけです。

改めてfa()の出力に戻ると，3,4列目のh2とu2はそれぞれ共通性と独自性を表しています。Q1_1の場合，共通性が0.16，独自性が0.84ということで，観測変数の分散（標準化されているので1）のうち0.16だけがこの2つの因子によって説明されていることになります。なおh2の値は単純な因子負荷の二乗和ではなく，回転後の因子間相関を考慮した $\mathrm{diag}(\tilde{\symbf{B}}^\top\symbf{\Phi}\tilde{\symbf{B}})$ の値になっています¹⁰。

6.6 因子分析の結果の続き

ここからは，先ほどfa()関数で得られた結果を見ながら，因子負荷以外の部分についても解説していきたいと思います。

コード 6.11: 改めて因子分析の結果を表示

res_fa

Factor Analysis using method =  minres
Call: fa(r = dat[, paste0("Q1_", 1:10)], nfactors = 2)
Standardized loadings (pattern matrix) based upon correlation matrix
        MR1   MR2   h2   u2 com
Q1_1  -0.08  0.42 0.16 0.84 1.1
Q1_2   0.00  0.68 0.47 0.53 1.0
Q1_3  -0.03  0.77 0.58 0.42 1.0
Q1_4   0.14  0.46 0.27 0.73 1.2
Q1_5   0.03  0.61 0.38 0.62 1.0
Q1_6   0.57 -0.05 0.31 0.69 1.0
Q1_7   0.64 -0.02 0.40 0.60 1.0
Q1_8   0.55  0.02 0.31 0.69 1.0
Q1_9   0.68  0.00 0.46 0.54 1.0
Q1_10  0.57  0.06 0.35 0.65 1.0

                       MR1  MR2
SS loadings           1.87 1.83
Proportion Var        0.19 0.18
Cumulative Var        0.19 0.37
Proportion Explained  0.51 0.49
Cumulative Proportion 0.51 1.00

 With factor correlations of 
     MR1  MR2
MR1 1.00 0.32
MR2 0.32 1.00

Mean item complexity =  1
Test of the hypothesis that 2 factors are sufficient.

df null model =  45  with the objective function =  2.14 with Chi Square =  5190.53
df of  the model are 26  and the objective function was  0.16 

The root mean square of the residuals (RMSR) is  0.04 
The df corrected root mean square of the residuals is  0.05 

The harmonic n.obs is  2432 with the empirical chi square  311.44  with prob <  1.1e-50 
The total n.obs was  2432  with Likelihood Chi Square =  379.19  with prob <  2.2e-64 

Tucker Lewis Index of factoring reliability =  0.881
RMSEA index =  0.075  and the 90 % confidence intervals are  0.068 0.082
BIC =  176.48
Fit based upon off diagonal values = 0.98
Measures of factor score adequacy             
                                                   MR1  MR2
Correlation of (regression) scores with factors   0.87 0.88
Multiple R square of scores with factors          0.76 0.78
Minimum correlation of possible factor scores     0.51 0.56

6.6.1 因子寄与率・分散説明率

                       MR1  MR2
SS loadings           1.87 1.83
Proportion Var        0.19 0.18
Cumulative Var        0.19 0.37
Proportion Explained  0.51 0.49
Cumulative Proportion 0.51 1.00

一番上のSS loadingsは因子負荷の二乗和(sum of squared loadings)を表していると思われます。実際には単純な二乗和 $\mathrm{diag}(\symbf{B}^\top\symbf{B})$ ではなく，これに回転後の因子間相関を考慮した値 $\mathrm{diag}(\tilde{\symbf{B}}^\top\symbf{\Phi}\tilde{\symbf{B}})$ が出ています¹¹。例えば因子1を例にとって見ると，因子1の得点 $\symbf{f}_{1}$ は，それぞれの項目に対する因子負荷量 $b_{1i}$ を通じて各項目の分散をある程度( $b_{1i}$ )説明します。ただ，因子1の影響はこれにとどまりません。因子2と相関があるということは， $\symbf{f}_{1}$ の値とある程度連動して $\symbf{f}_{2}$ の値も変化します。仮にこの相関関係を回帰分析的に言えば， $\symbf{f}_{1}$ は $\symbf{f}_{2}$ に対して僅かな分散説明率を持っているわけです。ということで， $\symbf{f}_{1}$ が $\symbf{f}_{2}$ を介して各項目に対してもつ僅かな分散説明率 $b_{2i}$ も合算されてSS loadingsが計算されています。

2つ目のProportion Varは，観測変数全体に対する各因子の分散説明率を表しています。今回は10項目のデータで因子分析を行っていますが，各観測変数は標準化されているため，分散の合計は10です¹²。この10に対して，因子1の寄与の合計(SS loadings)は1.87なので，Proportion Varは0.187となります。つづくCumulative Varは，その分散説明率の累積（累積寄与率）です。今回の場合，因子1と因子2はそれぞれ0.187および0.183という分散説明率（因子寄与率）なので，第二因子のCumulative Varには，その合計で0.370という値が入るわけです。言い換えると，今回の分析では2因子でこの10項目の分散のうちおよそ37%が説明される，ということになります。このCumulative Varの値があまりにも低い場合は，まだ各項目の独自性が高すぎる（＝共通因子の数が少ないかも）ということです。せっかく因子得点を算出しても，結局各項目への回答はその因子以外の要因で決まっている割合が大きいということになり，因子得点の意味が問われてしまいます。もうお分かりかもしれませんが，因子分析では因子の数を増やすほど累積寄与率は上がるので，累積寄与率が一定の値になるまで因子数を増やすというアプローチも無いことは無いでしょう¹³。

一番下の2つProportion ExplainedとCumulative Proportionは，共通因子で説明可能な部分のうち，各因子が占める割合（および累積割合）を表しています。ここまで解釈することはあまり無い気がしますが，例えばProportion Explainedが低すぎる因子がある場合には，相対的に「なくても良い」という判断に使えるかもしれませんね。

6.6.2 因子間相関

 With factor correlations of
     MR1  MR2
MR1 1.00 0.32
MR2 0.32 1.00

見ての通り，回転後の因子間の相関行列 $\symbf{\Phi} = (\symbf{A}\symbf{A}^\top)^{-1}$ です。相関があまりに高い場合には，もしかしたら因子を統合してしまっても良いのかもしれません。もちろん内容次第ですが。

他にも下の方にはいろいろな値が出ていますが，因子分析の結果を解釈するだけならとりあえずここまで理解できていれば十分です。ということで，続いては得られた因子負荷を所与として，因子得点の計算に進みましょう。

6.6.3 因子得点

実は因子得点 $\symbf{F}$ は，fa()の出力の中に$scoresという名前で入っています。

コード 6.12: 因子得点を出す

head(res_fa$scores)

          MR1        MR2
1 -1.38258689 -0.8922837
2 -0.34481092 -0.2707195
3 -0.11683020 -0.4538879
4 -1.08523045  0.1082199
5 -0.06184927 -0.8948835
6  1.35556644  0.4285821

観測された因子得点の相関を見てみると，モデル上の回転後の因子間相関 $\symbf{\Phi}$ とは少し異なります。報告する際には気をつけてください。

コード 6.13: 因子得点の相関とモデル上の因子間相関は別もの

cor(res_fa$scores)

         MR1      MR2
MR1 1.000000 0.392582
MR2 0.392582 1.000000

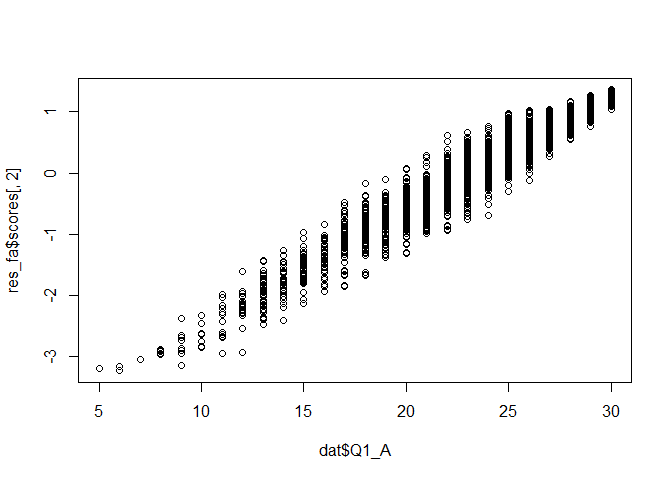
図 6.17 は因子得点と合計点の散布図です。確かに合計点が高い人ほど因子得点も高くなっているようです。

コード 6.14: 因子得点と合計点の散布図

# MR2はQ1_1からQ1_5に対応 == Q1_A
plot(dat$Q1_A, res_fa$scores[, 2])

尺度得点として，合計点の代わりに因子得点を用いることのメリットは大きく分けて2つあると考えます。 1つ目は，得点のばらつきです。図 6.17 を見るとわかるように，合計点が同じ人であっても因子得点はかなりばらつきがあります。この理由は，項目ごとに因子負荷が異なるためです。因子負荷が高いほど，因子得点が高い人と低い人を明確に識別できる項目です。したがって，因子負荷が高い項目に「とても当てはまる」と回答した人はかなりの確度で因子得点が高いといえます。一方で，因子負荷がほぼゼロの項目では，因子得点が高いから「当てはまる」と回答しているとはいえません。したがって，この項目に「とても当てはまる」と回答した人の因子得点が高いという保証はありません。尺度得点として合計点を使うということは，このように各項目が因子得点の推定に与える情報の強さを無視して，一律同じパワーを持っていると仮定していることと同じです。そのため，特に因子負荷がばらつくような状況下では，単純な合計点がその人の潜在的な特性の強さを正確に表しているとはあまり言えないかもしれないのです¹⁴。

因子得点を用いるもう一つのメリットは，モデル上は誤差が分離されるという点です。図 6.4 にあるように，因子分析モデルでは各項目への回答は「共通因子」と「独自因子」の影響を受けていると考えます。このとき，誤差（特に偶然誤差）は，他の項目とは無関係に生じるものなので独自因子の中に吸収されているという見方ができます。したがって，共通因子の部分には誤差の影響は含まれていないと考え，因子得点はある意味では純粋な値として扱うことができる，とされているのです。

6.7 カテゴリカル因子分析

（ここからは因子分析を行うにあたってのプラクティカルな話題をいくつか紹介します。）

因子分析では，相関行列をもとに因子負荷行列を求めています。その相関行列に関して， Section 4.3.2 では，カテゴリカル変数の場合の特別な相関（ポリシリアル相関）の話をしました。因子分析の時にも同じことが言えます。

ここまでは，観測されたデータを普通の連続変数とみなして因子分析を行ってきましたが，心理尺度のようにカテゴリカルな観測変数の場合には，相関係数が過小評価されてしまうため，結果的に共通因子のパワーも弱く評価されてしまいます。つまり，因子分析での項目間の相関関係は，本当は背後にある潜在的な値に対して求められるべきです。そこで，因子分析に用いる相関をピアソンの積率相関係数ではなくポリコリック相関（カテゴリカル変数同士の相関係数）に変更することを考えます。このように，各観測変数を連続変数（間隔尺度）ではなく順序尺度とみなして因子分析を行うことをカテゴリカル因子分析と呼んだりします。

Section 4.3.2 では，ポリシリアル相関などのカテゴリカルな相関を計算するためのパッケージとしてpolycorを紹介しました。ポリコリック相関を計算する関数はこのパッケージの中にも（polychor()）あるのですが，データフレーム全体に対して相関行列を計算することは出来ないので，ここでは別の関数を使用します¹⁵。

psychパッケージにあるpolychoric()関数を使用しましょう。

コード 6.15: ポリコリック相関を計算する

# 毎回列名を指定するのが面倒なので先に作っておく
cols <- paste0("Q1_", 1:10)
cor_poly <- polychoric(dat[, cols])
cor_poly

Call: polychoric(x = dat[, cols])
Polychoric correlations 
      Q1_1 Q1_2 Q1_3 Q1_4 Q1_5 Q1_6 Q1_7 Q1_8 Q1_9 Q1_10
Q1_1  1.00                                              
Q1_2  0.42 1.00                                         
Q1_3  0.33 0.57 1.00                                    
Q1_4  0.19 0.41 0.43 1.00                               
Q1_5  0.24 0.45 0.58 0.37 1.00                          
Q1_6  0.02 0.12 0.14 0.11 0.17 1.00                     
Q1_7  0.00 0.15 0.16 0.26 0.14 0.49 1.00                
Q1_8  0.03 0.22 0.15 0.16 0.15 0.35 0.40 1.00           
Q1_9  0.14 0.20 0.17 0.22 0.17 0.43 0.45 0.41 1.00      
Q1_10 0.05 0.16 0.19 0.29 0.20 0.31 0.34 0.40 0.54 1.00 

 with tau of 
         1    2      3       4    5
Q1_1  -1.9 -1.2 -0.743 -0.3262 0.43
Q1_2  -2.1 -1.5 -1.179 -0.4783 0.48
Q1_3  -1.8 -1.3 -0.963 -0.3284 0.61
Q1_4  -1.7 -1.1 -0.877 -0.3756 0.23
Q1_5  -2.0 -1.3 -0.909 -0.2425 0.68
Q1_6  -2.0 -1.4 -0.917 -0.2308 0.77
Q1_7  -1.9 -1.2 -0.764 -0.1126 0.84
Q1_8  -1.9 -1.2 -0.757 -0.0072 0.95
Q1_9  -2.0 -1.2 -0.632 -0.1678 0.60
Q1_10 -1.3 -0.6 -0.014  0.2884 0.92

polychoric()は，相関行列に加えて各項目のカテゴリ閾値（tau）をlist形式で返します。その中からポリコリック相関行列そのものを出力したい場合にはcor_poly$rhoで取り出すことが出来ます。あとはこれをfa()関数に与えるだけです。これまでfa()関数にはデータフレームを与えてきましたが，中でやっているのは結局「相関行列を計算する→因子負荷行列の初期解を計算する→回転する」なので，実は相関行列を直接与えることも可能です。¹⁶

fa()関数に相関行列を直接与える場合は，引数n.obsが必要になります。これは因子負荷の計算自体には必要ないのですが，fa()の出力でいうと下の方に表示される検定などに必要な情報です。欠測値がある場合には厄介なのですが，事前に欠測のあるデータを削除している場合には普通にnrowで大丈夫です。

コード 6.16: カテゴリカル因子分析(1)：相関行列を与える

res_fa_cat <- fa(cor_poly$rho, nfactors = 2, n.obs = nrow(dat))
res_fa_cat

Factor Analysis using method =  minres
Call: fa(r = cor_poly$rho, nfactors = 2, n.obs = nrow(dat))
Standardized loadings (pattern matrix) based upon correlation matrix
        MR2   MR1   h2   u2 com
Q1_1  -0.09  0.48 0.21 0.79 1.1
Q1_2   0.00  0.74 0.55 0.45 1.0
Q1_3  -0.03  0.81 0.65 0.35 1.0
Q1_4   0.16  0.49 0.32 0.68 1.2
Q1_5   0.04  0.64 0.43 0.57 1.0
Q1_6   0.62 -0.04 0.36 0.64 1.0
Q1_7   0.68 -0.03 0.45 0.55 1.0
Q1_8   0.58  0.02 0.35 0.65 1.0
Q1_9   0.72  0.01 0.53 0.47 1.0
Q1_10  0.60  0.06 0.39 0.61 1.0

                       MR2  MR1
SS loadings           2.11 2.11
Proportion Var        0.21 0.21
Cumulative Var        0.21 0.42
Proportion Explained  0.50 0.50
Cumulative Proportion 0.50 1.00

 With factor correlations of 
     MR2  MR1
MR2 1.00 0.34
MR1 0.34 1.00

Mean item complexity =  1
Test of the hypothesis that 2 factors are sufficient.

df null model =  45  with the objective function =  2.78 with Chi Square =  6749.62
df of  the model are 26  and the objective function was  0.22 

The root mean square of the residuals (RMSR) is  0.04 
The df corrected root mean square of the residuals is  0.05 

The harmonic n.obs is  2432 with the empirical chi square  367.22  with prob <  5.9e-62 
The total n.obs was  2432  with Likelihood Chi Square =  540.84  with prob <  1.2e-97 

Tucker Lewis Index of factoring reliability =  0.867
RMSEA index =  0.09  and the 90 % confidence intervals are  0.084 0.097
BIC =  338.13
Fit based upon off diagonal values = 0.98
Measures of factor score adequacy             
                                                   MR2  MR1
Correlation of (regression) scores with factors   0.89 0.91
Multiple R square of scores with factors          0.79 0.82
Minimum correlation of possible factor scores     0.58 0.64

本Chapterの前半では，ピアソンの積率相関係数を使って因子分析を行っていましたが，それと比べると因子負荷の値が基本的には大きくなっています。 もともと相関係数が過小推定されていたために，因子負荷も過小推定されていたと考えるのが妥当でしょう。今回カテゴリカル因子分析を行ったことによって，より正しい因子負荷量を求めることができたといえます。

こんな感じで，カテゴリカル因子分析をするためにはポリコリック相関行列を計算しておく必要があるのですが，もう少しラクな方法もあります。実はpsych::fa()では，使用する相関係数を引数corによって指定することが出来ます。

コード 6.17: カテゴリカル因子分析(2)：fa()関数に計算させる

res_fa_cat <- fa(dat[, cols], nfactors = 2, cor = "poly")
res_fa_cat

Factor Analysis using method =  minres
Call: fa(r = dat[, cols], nfactors = 2, cor = "poly")
Standardized loadings (pattern matrix) based upon correlation matrix
        MR2   MR1   h2   u2 com
Q1_1  -0.09  0.48 0.21 0.79 1.1
Q1_2   0.00  0.74 0.55 0.45 1.0
Q1_3  -0.03  0.81 0.65 0.35 1.0
Q1_4   0.16  0.49 0.32 0.68 1.2
Q1_5   0.04  0.64 0.43 0.57 1.0
Q1_6   0.62 -0.04 0.36 0.64 1.0
Q1_7   0.68 -0.03 0.45 0.55 1.0
Q1_8   0.58  0.02 0.35 0.65 1.0
Q1_9   0.72  0.01 0.53 0.47 1.0
Q1_10  0.60  0.06 0.39 0.61 1.0

                       MR2  MR1
SS loadings           2.11 2.11
Proportion Var        0.21 0.21
Cumulative Var        0.21 0.42
Proportion Explained  0.50 0.50
Cumulative Proportion 0.50 1.00

 With factor correlations of 
     MR2  MR1
MR2 1.00 0.34
MR1 0.34 1.00

Mean item complexity =  1
Test of the hypothesis that 2 factors are sufficient.

df null model =  45  with the objective function =  2.78 with Chi Square =  6749.62
df of  the model are 26  and the objective function was  0.22 

The root mean square of the residuals (RMSR) is  0.04 
The df corrected root mean square of the residuals is  0.05 

The harmonic n.obs is  2432 with the empirical chi square  367.22  with prob <  5.9e-62 
The total n.obs was  2432  with Likelihood Chi Square =  540.84  with prob <  1.2e-97 

Tucker Lewis Index of factoring reliability =  0.867
RMSEA index =  0.09  and the 90 % confidence intervals are  0.084 0.097
BIC =  338.13
Fit based upon off diagonal values = 0.98
Measures of factor score adequacy             
                                                   MR2  MR1
Correlation of (regression) scores with factors   0.89 0.91
Multiple R square of scores with factors          0.79 0.82
Minimum correlation of possible factor scores     0.58 0.64

結果は先程と同じになっているはずです。

ちなみに萩生田・繁桝（1996）では，シミュレーション研究をもとに，多くの場合はピアソンの積率相関係数で十分（ポリコリック相関と大差ない）という結論を出していたりもします。数理的に厳密なのはポリコリック相関ですが，実際には不適解を出してしまったり，回答者のいないカテゴリがあると面倒だったりと，実用上は問題点もあったりします。また，ポリコリック相関係数を安定的に推定するためにはデータが数百はあることが望ましいです。そのため，まずはカテゴリカル因子分析をやってみて，解が得られない or 不安定な場合には普通にピアソンの積率相関を用いた方法にしても良いのではないかと思います。

6.8 （おまけ）因子分析をする前に

因子分析は，複数の観測変数の背後に共通の要因が存在し，また観測変数間の相関関係がその共有の要因のみによって説明される，というモデルを仮定した分析です。したがって，因子分析を行う前には

そもそも観測変数の間には相関関係が存在しており，
その相関関係が，（特定の２変数間の関係ではなく）概ね全ての観測変数群の関係性によって説明可能である

ことを確認すると良いかもしれません。２点目がちょっと分かりづらいかもしれませんが（言葉でどう説明したら良いのか迷いました），これは図 6.9 にあるような，全ての観測変数に共通する相関の要因（共通因子）とは異なる「共通因子では説明できない要因」によって２変数の相関が規定されてほしくない，ということを意味しています。そこで，この節では上記の２つを検証するための方法¹⁷を簡単に紹介します。

6.8.1 Bartlettの球面性検定

Bartlettの球面性検定（Bartlett, 1950, 1951）では，共通因子の影響を除いたあとの「独自因子得点の相関行列」 $\symbf{\Psi}$ が単位行列である，という帰無仮説を立てて検定を行っています。具体的には，以下の検定統計量（Browne, 1968） $\chi^2_m = -\left(P-\frac{2I+11}{6}-\frac{2T}{3}\right)\mathrm{ln}|\symbf{\Psi}| \qquad(6.33)$ が自由度 $\frac{1}{2}\left[(I-T)^2-I-T\right]$ の $\chi^2$ 分布に漸近的に従うことを利用して統計的仮説検定を行います。念のため再度示しておきますが，

[ $P$ ]: 回答者( $P$ erson)の数
[ $I$ ]: 項目( $I$ tem)の数
[ $T$ ]: 共通因子( $T$ rait)の数

を表しています。また， $|\symbf{\Psi}|$ は $\symbf{\Psi}$ の行列式を表しています。細かい式の意味はともかく，重要なのは $\chi^2_m$ の中の $\mathrm{ln}|\symbf{\Psi}|$ の部分です。 $\symbf{\Psi}$ に限らず，相関行列（全ての対角成分が1）の行列式の値は必ず0から1の間の値になること，そして行列式の値が1になるのは単位行列（全ての変数間が無相関）の場合であることが知られています¹⁸。したがって，その対数を取った $\mathrm{ln}|\symbf{\Psi}|$ は，変数間の相関が高いほど大きなマイナスの値を取るようになっています。ということで，これの符号をひっくり返すことで，検定統計量 $\chi^2_m$ は相関行列 $\symbf{\Psi}$ の「全体としての相関の強さ」を表しているといえるわけです。

そんなBartlett検定ですが，検定の目的からすると，帰無仮説「 $\symbf{\Psi}$ が単位行列である」が棄却されなければ嬉しいような気がします。しかし実際には，独自因子間の相関を検証する目的，つまり因子分析の結果得られた $\symbf{\Psi}$ に対してBartlettの球面性検定を使用することは現状ほぼ無いようです。

実際のBartlettの球面性検定（SPSSで出力される結果）では，共通因子の数が0（ $T=0$ ）であると設定して検定を行います。 このとき「独自因子得点の相関行列」 $\symbf{\Psi}$ イコール「観測変数の相関行列」 $\symbf{\Sigma}$ となるため，球面性検定の帰無仮説は「観測変数の相関行列が単位行列である」，すなわち全ての観測変数は無相関であると見ることができます。この場合，帰無仮説が棄却されてくれれば「観測変数間に相関関係がある」ことが言えるため，共通因子を置いた因子分析を行う意味があると言えるわけです。

Rでは，psychパッケージにcortest.bartlett()という関数が用意されています。

コード 6.18: Bartlettの球面性検定

# cor_polyはpsych::polychoric()で既に出している相関行列
# listの中のrhoがポリコリック相関行列の本体なので
cortest.bartlett(cor_poly$rho, n = nrow(dat))

$chisq
[1] 6749.621

$p.value
[1] 0

$df
[1] 45

出力されたp.valueが0.05より小さければ帰無仮説が棄却されて「因子分析をやる意味あり」ということになるのですが，上の $\chi^2_m$ の式からもわかるように，この方法も一般的な統計的仮説検定の例に漏れず，サンプルサイズがある程度大きくなったらほぼ確実に有意になってしまいます。そして，そもそも心理尺度のようなデータでは，観測変数間の相関がゼロなんてことは相当の大失敗でもしない限りあり得ないはずです。その意味では，Bartlettの球面性検定は（回帰分析におけるF検定と同様）しなかったところで大した問題ではないと言えるでしょう¹⁹。

6.8.2 KMO (Kaiser-Meyer-Olkin)

続いては，独自因子に起因する相関があるかを確認する方法を紹介します。ここではKMO (Kaiser-Meyer-Olkin)またはMSA (measure of sampling adequacy)と呼ばれる指標（Kaiser, 1970）を紹介します。

KMOはイメージ分析（Guttman, 1953）と呼ばれる方法に基づく考え方です。これは，複数の観測変数間の相関関係に関する多変量解析法として，主成分分析・因子分析に続く第３の方法として提案されたものらしく，因子分析のような不定性が無いことや，（多変量正規）分布の仮定が必要ないという点で因子分析よりもgeneralな方法とされています（が，現状あまり使われていないと思います…）。

イメージ分析では，各観測変数 $x_i$ について「それ以外の全ての観測変数」を用いた重回帰分析を行います。 $\begin{aligned} \begin{split} x_i &= \hat{x_i} + e_i \\ \hat{x_i} &= w_1x_1 + w_2x_2 + \cdots + w_{i-1}x_{i-1} + w_{i+1}x_{i+1} + \cdots + w_Ix_I \end{split} \end{aligned} \qquad(6.34)$

すると，観測変数 $x_i$ は「いずれかの観測変数と関係がある部分」 $\hat{x_i}$ と「いずれの観測変数とも関係がない部分」 $e_i$ に分けることができます。そしてイメージ分析では， $\hat{x_i}$ のことをイメージスコア， $e_i$ のことを反イメージスコアと呼びます。式からもなんとなく分かるように，イメージスコア $\hat{x_i}$ は，他の観測変数と（相関）関係がある部分を表しているため，これは因子分析の文脈では共通因子得点に相当しています。同様に，反イメージスコアは独自因子得点に相当するわけです。したがって，反イメージスコアの相関行列を見ることによって，図 6.9 に示されるような共通因子では取り切れない「独自因子間の相関」を見ることができる，という考えに至ります。

具体的なやり方としては，まず反イメージスコアの相関行列を以下の式（Kaiser, 1970）によって求めます。 $\begin{aligned} \begin{split} \symbf{Q} &= \symbf{S}\symbf{\Sigma}^{-1}\symbf{S} \\ \symbf{S} &= \mathrm{diag}(\symbf{\Sigma}^{-1})^{-1/2} \end{split} \end{aligned} \qquad(6.35)$ なんだかややこしい式ですが，最終的に得られる行列 $\symbf{Q}$ の各要素は，対応する２変数の反イメージスコアの相関係数＝「それ以外の全ての観測変数」の影響を除いた偏相関係数に等しくなっています。つまり， $\symbf{Q}$ の非対角成分が０に近いほど「観測変数間の相関の大部分が他の観測変数との共通成分で説明できる」≒共通因子のようなものがあることを意味するため，因子分析を行うことが妥当であると示されるわけです。

ここまでの背景を説明して，ようやくKMOの登場です。KMOは上で説明したものをまとめて一つの指標としたもので， $\begin{aligned} \mathrm{KMO} = \frac{\sum\sum_{i\neq j} r_{ij}^2}{\sum\sum_{i\neq j} r_{ij}^2 + \sum\sum_{i\neq j} q_{ij}^2} \end{aligned} \qquad(6.36)$ という式で表されます（Kaiser & Rice, 1974）。ここで $r_{ij}, q_{ij}$ はそれぞれデータから計算された相関行列 $\symbf{\Sigma}$ と反イメージ相関行列 $\symbf{Q}$ における変数 $i,j$ の相関係数を表しています。つまり，KMOは「そもそも観測変数間には十分な相関 $r_{ij}$ がある」かつ「他の変数と無関係な独自成分同士の相関 $q_{ij}$ は小さい」という程度を表した指標と言えるでしょう。

なお，KMOは上述のようにデータ全体に対してだけでなく，各変数ごとに計算することもできます。といっても考え方は簡単で，上の式を特定の変数の列のみで計算したら良いだけです。 $\begin{aligned} \mathrm{KMO}_i = \frac{\sum_{j = 1,\cdots i-1,i+1,\cdots,I} r_{ij}^2}{\sum_{j = 1,\cdots i-1,i+1,\cdots,I} r_{ij}^2 + \sum_{j = 1,\cdots i-1,i+1,\cdots,I} q_{ij}^2} \end{aligned} \qquad(6.37)$ $\mathrm{KMO}_i$ が低い場合，その変数は他の変数との相関がそもそも強くない可能性が高いため，因子分析から除外することを検討すると良いかもしれません。

Rでは，psychパッケージにKMO()という関数が用意されています。

コード 6.19: KMO（またの名をMSA）

# cor_polyは先程計算済みのポリコリック相関
KMO(cor_poly$rho)

Kaiser-Meyer-Olkin factor adequacy
Call: KMO(r = cor_poly$rho)
Overall MSA =  0.8
MSA for each item = 
 Q1_1  Q1_2  Q1_3  Q1_4  Q1_5  Q1_6  Q1_7  Q1_8  Q1_9 Q1_10 
 0.76  0.80  0.78  0.84  0.82  0.80  0.79  0.85  0.79  0.79

出力のうち，Overall MSAがデータ全体に計算したKMOの値です。また，MSA for each item =以下に示されているのが，変数ごとに計算した $\mathrm{KMO}_i$ の値です。具体的にどの程度あれば良いか，というのはあまり明確ではないような気もしますが， Kaiser （1974）では，以下のような基準を示しています。

表 6.4: KMOの基準（Kaiser, 1974）

値	評価
.9以上	marvelous
.8以上	meritorious
.7以上	middling
.6以上	mediocre
.5以上	miserable
.5未満	unacceptable

ということで，Overall MSAの値が0.5以上であればとりあえず”acceptable”と言えるようにも見えますが，式の定義からすると，KMOが0.5になるのは「データにおける相関係数」と「反イメージ相関係数」が同じ大きさの場合なので，実質的に共通因子が存在しないようなケース（各変数を独立に乱数生成した場合とか: Shirkey & Dziuban, 1976）に相当すると考えられます。そういうわけで，実際にデータ分析をする際には，なんとなくですが0.8くらいはあったほうが良いのではないか，という気がします²⁰。

6.9 回転の方法

Section 6.5.1 では，回転のメカニズムおよびその目的を説明しました。回転するためには，回転後の因子負荷行列がいい感じに単純構造に近づくように回転行列を指定する必要があります。そのためには，「いい感じ」の基準を決めなければいけません。

そもそも「単純構造」とは何なのでしょうか。 Thurstone （1947）による具体的(にして理想的)な単純構造の条件は以下のとおりです。

各項目は少なくとも1つの因子に対して因子負荷が0であること
各因子は少なくとも因子数 $T$ 個の項目に対して因子負荷が0であること
2つの因子に着目した場合に，一方の因子の要素は0で他方の因子の要素は0でない項目があること（＝異なる因子を識別可能な項目が存在すること）
因子数が4以上の時に，そのうち2つの因子に着目した場合に，どちらの要素も0である項目があること
2つの因子に着目した場合に，どちらの要素も0である項目が少ないこと

この「単純構造」の条件になるべく近づけるための回転の方法について，数多くの基準が提案されてきました。fa()関数で利用可能なもののうち，有名と思われるものについていくつか紹介します（基本的な回転法の整理およびレビューについては Browne, 2001 などを参照）。

6.9.1 直交回転系

直交回転で最も有名なのはバリマックス回転 (varimax rotation) でしょう。この方法では，因子負荷行列に対して $\begin{aligned} \sum_{t=1}^{T}\left\{\sum_{i=1}^{I}{(b_{ti}^2)}^2 - \frac{1}{I}\left(\sum_{i=1}^{I}b_{ti}^2\right)^2\right\} \end{aligned} \qquad(6.38)$ という目的関数が最大になるように回転を行います。最初の $\sum$ 記号によって，この計算が「列ごとに何かを計算したものの総和を求めている」ということがわかります。列ごとに求めているものは，因子負荷量の二乗の分散のようなものです。ある変数 $x$ の分散を求める方法として， $\begin{aligned} \sigma_x^2=\frac{1}{n}\sum x^2 - \left(\frac{1}{n}\sum x\right)^2 \end{aligned} \qquad(6.39)$ というものがありました。すこし調整の項があったりしますが，基本的にはこれと同じようなことをしている（ $x$ のところに $b_{ti}$ が入っている）わけです。 varianceをmaxにするのでvari-maxという名前なわけですね。直感的には，因子負荷の分散の二乗和が最大になるようにしてやると，それぞれの因子について「負荷が高い観測変数」と「負荷が低い観測変数」があることになるため，単純構造の条件2に近づきそうです。

6.9.2 斜交回転系

斜交回転で最も有名なのはプロマックス回転 (promax rotation) だと思います。プロマックス回転ではプロクラステス回転²¹ (procrustes rotation) をベースに回転を行うため，まずはプロクラステス回転の説明をしておきます。プロクラステス回転では，回転のゴールをただの単純構造ではなく，仮説や理論から導き出されるターゲット行列に設定し，ターゲット行列とのズレが最小になるように回転を行います。ターゲット行列には，例えば先行研究で観測された因子負荷行列などを設定することができるのですが，そのような行列を探してきて設定するのは結構大変なことです。そこでプロマックス法では，まずバリマックス法などの直交回転による回転を行い，得られた因子負荷行列を調整することでターゲット行列をデータから作成します。具体的には，バリマックス回転で得られた因子負荷行列について，値が大きい要素はより大きく，値が小さい要素はより小さくすることで，バリマックス解よりもさらに「理想に近い」行列を作成しています。プロマックス回転は，それ自体が「単純構造」に向かって何らかの基準を最適化する方法ではありません。バリマックス回転をベースに解を求めているということは，例えばそもそもバリマックス回転でうまく単純構造が出なかった場合には失敗する可能性があります。計算量が少ないことなどから昔はよく使われていた方法のようです。

プロマックス回転よりももっと直接的に，できるだけ完全な単純構造（完全クラスター解）に近づけたい場合には，いっそターゲット行列を完全クラスター解になるように作ってしまえば良いでしょう。 独立クラスター回転 （Harris-Kaiser independent cluster rotation: Kiers & Ten Berge, 1994） ²² はそのような考え方に基づいています。方法はとてもシンプルで，まずバリマックス回転で因子負荷行列の直交解をもとめ，その行列の各行の中で絶対値が最も大きい（各項目が最も高い負荷を持っている共通因子）1つをその符号に応じて $\pm 1$ ，その他を0としたターゲット行列を設定し，これに向けてプロクラステス回転を行います。当然「完全クラスター解にできるだけ近づくように」回転されるので，各項目は1つの共通因子にのみ高い負荷を持った構造になりやすいと言えます。

fa()関数のデフォルトはオブリミン回転 (oblimin rotation) と呼ばれる方法です。実際には，コーティミン回転 (quartimin rotation) と呼ばれる方法を行っているような気がします²³。コーティミン回転では，以下の基準を最小化します。 $\sum_{t=1}^{T}\sum_{s\neq t}^{T}\left\{\sum_{i=1}^{I}{b_{ti}^2b_{si}^2}\right\} \qquad(6.40)$ 最初の2つの $\sum$ 記号によって，因子のペアごとに何かしらの計算を行い総和を求めていることがわかります。その中身は同じ項目 $i$ に対する因子負荷の二乗の積です。この式は，同じ項目に因子 $t$ と因子 $s$ が両方とも高い因子負荷を持っていた場合にのみ大きな値になります。したがって，コーティミン基準を最小化するということは特に単純構造の条件3を目指している，と言えるでしょう。

他によく使われる気がするのは，ジオミン回転 (geomin rotation) でしょうか²⁴。この方法では，以下の目的関数を最小化するように回転を行います。 $\sum_{i=1}^{I}\left\{\prod_{t=1}^{T}{b_{ti}^2}\right\}^{\frac{1}{T}} \qquad(6.41)$ 波括弧の中は，因子負荷の二乗をすべてかけたものを求めています。したがって，ジオミン回転では項目ごとに因子負荷の二乗の幾何平均 (geometric mean) を計算して，その総和を取っているのです。幾何平均は上の式からも分かるように，一つでも0に近い要素があれば小さな値になります。したがって，Thurstoneの基準の1番を直接的に達成しようとしている基準と言えます。一方で，0に近い要素が1個以上ならば，2個でも3個でも幾何平均はあまり変わらないので，各変数が複数の因子に高い負荷を持つこと (cross-loading) を許容しやすい回転法と言われています。完全な単純構造がそもそもあまり期待されないような場合には良いかもしれません。

ここで紹介した以外にも，因子の回転法はかなりたくさんあります。その中でどれを使えばよいかについては，特に決まっていない（個人の好みな）気がします。強いて言うなら，大抵の場合は斜交回転をしておけば良いでしょう。方法によって，因子間相関が高く出やすいものがあれば低く出やすいもの，単純構造に近づきやすいものや近づきにくいものなどがあるので，いろいろな方法を試してみていい感じの因子負荷行列になる回転法を選べば良いのではないかと思います。

fa()関数では，引数rotateによって回転法を指定することができます。これまでは指定していなかったのでrotate="oblimin"になっていたわけですが，試しに直交回転であるバリマックス回転で因子負荷を求めてみましょう。

コード 6.20: 直交（バリマックス）回転

res_fa_varimax <- fa(dat[, cols], nfactors = 2, cor = "poly", rotate = "varimax")
res_fa_varimax

Factor Analysis using method =  minres
Call: fa(r = dat[, cols], nfactors = 2, rotate = "varimax", cor = "poly")
Standardized loadings (pattern matrix) based upon correlation matrix
        MR1  MR2   h2   u2 com
Q1_1  -0.01 0.45 0.21 0.79 1.0
Q1_2   0.13 0.73 0.55 0.45 1.1
Q1_3   0.12 0.80 0.65 0.35 1.0
Q1_4   0.24 0.51 0.32 0.68 1.4
Q1_5   0.15 0.64 0.43 0.57 1.1
Q1_6   0.60 0.06 0.36 0.64 1.0
Q1_7   0.66 0.09 0.45 0.55 1.0
Q1_8   0.58 0.12 0.35 0.65 1.1
Q1_9   0.71 0.14 0.53 0.47 1.1
Q1_10  0.61 0.16 0.39 0.61 1.1

                       MR1  MR2
SS loadings           2.12 2.11
Proportion Var        0.21 0.21
Cumulative Var        0.21 0.42
Proportion Explained  0.50 0.50
Cumulative Proportion 0.50 1.00

Mean item complexity =  1.1
Test of the hypothesis that 2 factors are sufficient.

df null model =  45  with the objective function =  2.78 with Chi Square =  6749.62
df of  the model are 26  and the objective function was  0.22 

The root mean square of the residuals (RMSR) is  0.04 
The df corrected root mean square of the residuals is  0.05 

The harmonic n.obs is  2432 with the empirical chi square  367.22  with prob <  5.9e-62 
The total n.obs was  2432  with Likelihood Chi Square =  540.84  with prob <  1.2e-97 

Tucker Lewis Index of factoring reliability =  0.867
RMSEA index =  0.09  and the 90 % confidence intervals are  0.084 0.097
BIC =  338.13
Fit based upon off diagonal values = 0.98
Measures of factor score adequacy             
                                                   MR1 MR2
Correlation of (regression) scores with factors   0.88 0.9
Multiple R square of scores with factors          0.77 0.8
Minimum correlation of possible factor scores     0.54 0.6

出力を見ると，直交回転なので因子間相関が出力されていません。また Section 6.7 で出したres_fa_cat（オブリミン解）と比べると，各項目について負荷量の低い側の因子の負荷量がやや大きめになっていることがわかります。このように，基本的には斜交回転のほうが単純構造に近い結果を得ることができるため，よっぽどの理由が無ければ斜交回転にしておくのがおすすめです。

6.10 モデルパラメータの推定法

Section 6.5 で紹介したモデルパラメータの推定法は，あくまでもひとつの方法です。因子分析におけるパラメータ（直交解）の推定法には，他にもいくつかの選択肢があります。

6.10.1 主因子法

一昔前のスタンダードだったのが主因子法です。基本的には Section 6.5 で説明したとおりです。固有値分解をして，固有値が大きい（ある意味「主たる」）因子から順に使っていく，というものでした。ただ Section 6.5 の説明だけでは実はまだ不十分です。

固有値分解は，観測変数間の相関行列 $\symbf{\Sigma}$ のうち，共通因子に起因する部分（つまり $\symbf{B}^\top\symbf{B}$ ）のみを対象とする話でした。しかし，私達の手元にあるのは $\symbf{B}^\top\symbf{B} + \symbf{\Psi}$ としての $\symbf{\Sigma}$ のみです。そして $\symbf{\Sigma}$ そのものを固有値分解したところで，本当に欲しい $\symbf{B}^\top\symbf{B}$ に相当する因子負荷行列を得ることは出来ません。

$\symbf{\Sigma}$ の対角成分の中から独自因子に起因する要素を取り除くためには，誤差共分散行列 $\symbf{\Psi}$ を特定する必要があります。しかし，私達の手元にあるのは $\symbf{B}^\top\symbf{B} + \symbf{\Psi}$ としての $\symbf{\Sigma}$ のみです。そして $\symbf{\Sigma}$ の対角成分に占める $\symbf{\Psi}$ の割合（＝独自性）は，「 $1-$ 共通性」として計算されるため，結局共通性が分からない限りこれはどうしようもありません…。

ということで，このままでは $\symbf{\Sigma}$ の対角成分が $\symbf{B}^\top\symbf{B}$ と $\symbf{\Psi}$ にどのように分解されているかが決められないので，解が一つに定まりません。これをクリアするため，（反復）主因子法では，以下の手順によって各変数の共通性の値を推定しながらモデルパラメータを求めています。

共通性の初期値を適当に決める
データの相関行列の対角成分を共通性の暫定値に置き換えた行列を固有値分解する
1. の結果をもとに改めて共通性を計算する
共通性の値が変わらなくなる（計算が収束する）まで2-3. を繰り返す
$\symbf{B}^\top\symbf{B} + \symbf{\Psi}$ の対角成分が1になるように $\symbf{\Psi}$ を決める

実は，主因子法によって得られる解は後述する最小二乗法と同じになるらしいです。ただ計算効率などの面から現在では最小二乗法のほうが用いられているようです。

6.10.2 最小二乗法

$\symbf{B}$ の推定に際しては，まず大前提として $\symbf{\Psi}$ の非対角成分はゼロ，すなわち共通因子の影響を取り除けば誤差共分散は全て消えるという仮定が重要となります。もし本当に誤差共分散が全てゼロなのであれば， $\symbf{\Sigma}$ と $\symbf{B}^\top\symbf{B}$ の非対角成分は完全に一致するはずです。そしてもちろん $\symbf{\Sigma}$ の対角成分と $\symbf{B}^\top\symbf{B} + \symbf{\Psi}$ の対角成分も完全に一致します（というかそうなるように $\symbf{\Psi}$ の要素を調整したら良い）。ですが，もちろん実際には共通因子数が $T<I$ である限りは非対角成分にはズレが生じてしまいます。最小二乗法および次に紹介する最尤法では，この「ズレ」を定量化したもの（不一致度関数）が最小になるようにパラメータを反復計算していきます。

最小二乗法はfa()関数のデフォルトになっている方法です。 $\left[(\symbf{B}^\top\symbf{B} + \symbf{\Psi}) - \symbf{\Sigma})\right]^2$ の対角成分の和（トレース）を計算すると，全ての非対角要素のズレの二乗和を求めることができます（対角要素のズレの二乗和は $0$ です）。あとはこれが最小になるように， $\symbf{B}$ と $\symbf{\Psi}$ を計算するだけです。

6.10.3 最尤法

共通因子と独自因子が多変量正規分布 $N\left(\symbf{\mu}, \symbf{S}\right) = \left(\begin{bmatrix} \symbf{0}_C \\ \symbf{0}_U \end{bmatrix},\begin{bmatrix} \symbf{\Phi}_{CC} & \symbf{0}_{CU} \\ \symbf{0}_{UC} & \symbf{I}_{UU} \end{bmatrix} \right) \qquad(6.42)$ に従うと仮定します。なお，添字の $C$ は共通因子に関する部分， $U$ は独自因子に関する部分を表しています。したがってここでは

共通因子，独自因子ともに平均はゼロ（ $\symbf{0}_C, \symbf{0}_U$ ）
共通因子同士の相関は認める（ $\symbf{\Phi}_{CC}\neq\symbf{0}$ ）
独自因子同士の相関は認めないので，対角成分が1の単位行列（ $\symbf{I}_{UU}$ ）
共通因子と独自因子の間は無相関（ $\symbf{0}_{CU}$ ）

ということが仮定されています。 Section 6.1 では，共通因子得点のスケールを「平均0, 分散1」にすると説明しましたが，最尤法では尤度関数を得るために，これに加えて（多変量）正規分布であるという仮定を置きます。

この仮定のもとでは，標準化された観測変数 $\symbf{y}$ は以下の多変量正規分布に従います。 $\symbf{y} \sim N(\symbf{0},\symbf{B}^\top\symbf{B} + \symbf{\Psi}) \qquad(6.43)$ あとは普通の最尤法に従って，データと最も整合的な（尤度が最大になる） $\symbf{B}$ および $\symbf{\Psi}$ を求めたら良いわけです。

最尤法は，最小二乗法などと比べると，データの多変量正規性を仮定しているなどの理由から，統計的に高度な方法となっています。そして一般的に，最尤推定量は一致性や有効性など，推定量として望ましい性質を持つことが知られています。そのため，計算がうまくいく場合には最小二乗法などよりも最尤法のほうが望ましいとされています。一方で，多変量正規性の仮定などが推定に悪影響を及ぼす場合があります。例えば「データが少ない」「因子数が必要以上に多い」といったときに共通性の推定値が1を超える (Heywood caseと呼ばれる)といった不適解が出てしまうこともしばしばあります。そのような場合には，最小二乗法などの別の方法によって推定を行うのが良いかもしれません。また，そもそも回答データが単峰にならないことが予測される（極端な選択肢が選ばれやすいと考えられる）ような場合には，最尤法は正しくない可能性があります。

fa()関数では，fmという引数によって因子の推定法を指定することが出来ます。試しに最尤法でやってみましょう。

コード 6.21: 因子の推定法を指定

# デフォルトはfm="minres"（最小二乗法）
# fm="pa"とすると主因子法もできる
res_fa_ml <- fa(dat[, cols], nfactors = 2, cor = "poly", fm = "ml")
res_fa_ml

Factor Analysis using method =  ml
Call: fa(r = dat[, cols], nfactors = 2, fm = "ml", cor = "poly")
Standardized loadings (pattern matrix) based upon correlation matrix
        ML2   ML1   h2   u2 com
Q1_1  -0.08  0.47 0.20 0.80 1.1
Q1_2   0.01  0.71 0.51 0.49 1.0
Q1_3  -0.03  0.82 0.66 0.34 1.0
Q1_4   0.16  0.49 0.32 0.68 1.2
Q1_5   0.03  0.67 0.46 0.54 1.0
Q1_6   0.61 -0.03 0.36 0.64 1.0
Q1_7   0.66 -0.02 0.43 0.57 1.0
Q1_8   0.58  0.02 0.34 0.66 1.0
Q1_9   0.73  0.00 0.54 0.46 1.0
Q1_10  0.62  0.05 0.41 0.59 1.0

                       ML2  ML1
SS loadings           2.12 2.11
Proportion Var        0.21 0.21
Cumulative Var        0.21 0.42
Proportion Explained  0.50 0.50
Cumulative Proportion 0.50 1.00

 With factor correlations of 
     ML2  ML1
ML2 1.00 0.34
ML1 0.34 1.00

Mean item complexity =  1
Test of the hypothesis that 2 factors are sufficient.

df null model =  45  with the objective function =  2.78 with Chi Square =  6749.62
df of  the model are 26  and the objective function was  0.22 

The root mean square of the residuals (RMSR) is  0.04 
The df corrected root mean square of the residuals is  0.05 

The harmonic n.obs is  2432 with the empirical chi square  377.19  with prob <  5.6e-64 
The total n.obs was  2432  with Likelihood Chi Square =  532.87  with prob <  5.4e-96 

Tucker Lewis Index of factoring reliability =  0.869
RMSEA index =  0.09  and the 90 % confidence intervals are  0.083 0.096
BIC =  330.16
Fit based upon off diagonal values = 0.98
Measures of factor score adequacy             
                                                   ML2  ML1
Correlation of (regression) scores with factors   0.89 0.91
Multiple R square of scores with factors          0.79 0.82
Minimum correlation of possible factor scores     0.59 0.64

今回のようにデータがきれいな場合には，最尤法でも問題なく解を得ることが出来ます。このような場合には，最尤法での結果を報告するほうが良いかもしれません。

6.11 因子数の決め方

因子分析では因子数を分析者が自由に選ぶことが出来ます。これまでは，datの最初の10項目を使って，因子数を2に決め打ちして因子分析を行っていました。あらかじめ因子数が分かっていたり，理論的に目処が立っている場合にはその因子数で分析を行えば良いのですが，尺度をボトムアップに作成するような場合や，自分が集めたデータでも先行研究と同様の因子構造が得られるかを検証する場合には，因子数はわからないことが多いです。ここでは，統計的に因子数を決定するためのいくつかの（伝統的な）基準を紹介します。比較的新しい（高度な）方法については，堀・牧野（2024）などを参照してください。

6.11.1 カイザー（・ガットマン）基準

因子分析は，データの相関行列（正確には独自性を除いた $\symbf{B}^\top\symbf{B}$ ）を固有値分解することで因子負荷行列を求めていました。このとき，各因子に対する因子負荷は固有ベクトルを固有値倍したもの（ $\sqrt{\lambda_t}\symbf{x}_t^\top$ ）として算出されていました。したがって，固有値こそが因子負荷の合計を決めており，ひいては分散説明率（共通性）の合計を規定しているということが言えます。実は， $I\times I$ 相関行列を固有値分解して得られる $I$ 個の固有値は，合計が必ず $I$ になるという性質があります。つまり，固有値は $I$ 個の項目に対する分散説明率を再配分した値である，とも言えそうです。イメージ的には，例えば第一因子に対する固有値（固有値の中の最大値）が3だとすると，その因子は一つで合計3項目分の分散を説明しているということです。 1個で3項目分の説明力を持っているということは，結果的に次元数を減らすことに役立っていると言えそうです。

このように考えると，固有値が1より小さい因子は1項目分の情報も持っていないことになるため，因子としてはザコと言えます。また，独自因子は1項目のみに影響を与えている因子なので，固有値を計算するとしたら1になります。この意味でも，固有値が1以下の因子はやはり要らなさそうです。この「固有値が1以上の因子のみを使う」という基準をカイザー（・ガットマン）基準と呼びます。カイザー基準は（未だに！）よく用いられている方法ですが，その問題点も長らく指摘されています。いくつかの研究によって，状況によって因子数を少なめに見積もったり（Cliff, 1988）多めに見積もったり（Zwick & Velicer, 1986）することが知られており，正しい因子数を出してくれるのはかなり限定的な状況のようです。言ってしまえば「カイザー基準は大雑把であり，それほどあてにならない」（堀，2005）ということで，現在ではあまり採用されない基準という印象があります。

6.11.2 スクリーテスト

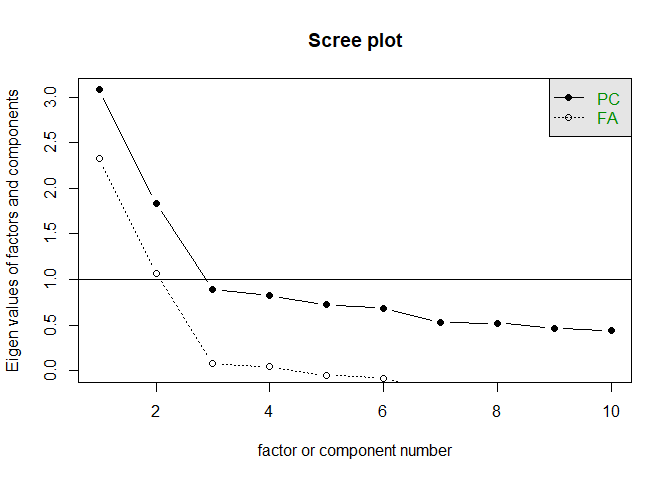
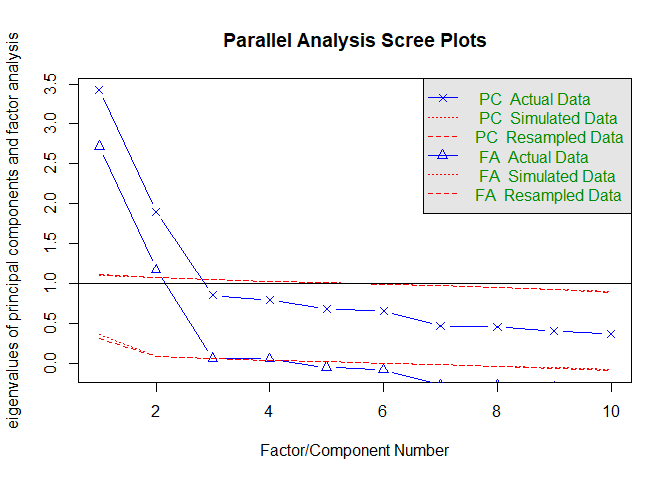
固有値を順に並べたものをスクリープロット (scree plot) と呼びます。 psychパッケージではscree()関数によって図 6.18 のように簡単にプロット可能です。

コード 6.22: スクリープロット

scree(dat[, cols])

なお，結果はFAの方を見てください。PCという方は主成分分析での結果です。ほとんどの場合主成分分析のプロットの方が上に来ます。なぜそうなるかは Section 6.13 を見てください。また，デフォルトではY軸が1のところに実線が引かれています。これは先程のカイザー基準を表しています。つまり今回の場合カイザー基準的には2因子が妥当ということになります。

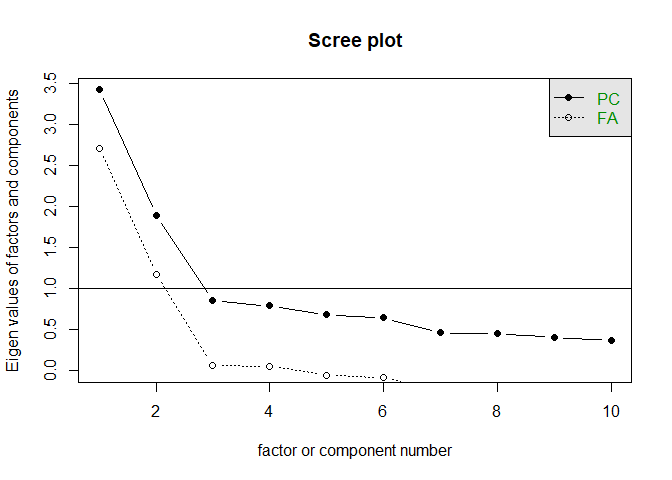
scree()関数にデータフレームを与えた場合には，そのデータフレームに対してピアソンの積率相関を求めて固有値を計算します。先程紹介したポリコリック相関に基づく固有値を見たい場合には，事前にポリコリック相関を計算しておき，それをscree()関数に与える必要があります。

コード 6.23: ポリコリック相関でスクリープロット

# cor_polyはpsych::polychoric()で既に計算済みのやつ
scree(cor_poly$rho)

あまり違いはないように見えますが，最初の因子を比べると，わずかに図 6.19 のほうが図 6.18 よりも大きな固有値になっているはずです。

このスクリープロットを用いて行うスクリーテスト (scree test)と呼ばれる因子数選択では，プロット的に傾きがなだらかになる手前の因子数を選択する，という方法です。図 6.18 や図 6.19 では，いずれも最初の2因子は傾きが強く，第3因子以降はなだらかになっています。したがってスクリーテスト的にも因子数は2が妥当，という判断ができます。

イメージ的には固有値分解では，まず第一固有値が「全てに共通する成分」をごっそり持っていきます。第2固有値以降は，その残りの中から共通成分を取り出していきます。したがって，あるところからはもう絞りカスしか残っていない状態になり，固有値的には下の方で大差ない状態になってしまいます。スクリーテストでは，この「下の方で大差ない状態」とくらべて如実に大きな固有値にはなにか意味があると考えて，その因子数を採用しているわけです。

ただ，今回のデータのように因子数がハッキリとしたきれいなデータではない場合には，これほどハッキリと変化点を見出すことが出来ないケースが結構多いです。そのような場合には客観的に因子数を決めづらかったりもするので，やはりまだアバウトな方法と言えそうです。

6.11.3 平行分析

カイザー基準では一律で1以上の固有値のある因子には意味がある，という判断をしていました。 平行分析 (parallel analysis) では，代わりに「乱数での固有値」との比較を行います。完全に乱数のデータでは本来相関は無いはずですが，標本誤差の関係などで相関が完全にゼロになることはありません。相関が完全にゼロではない限りは，固有値分解を行うと第一固有値の値は1よりも少しだけ大きくなります。試しにやってみましょう。

コード 6.24: 乱数で固有値を出してみる

# 1000行10列の一様乱数行列
dat_rnd <- matrix(runif(10 * 1000), ncol = 10)
eigen(cor(dat_rnd))

eigen() decomposition
$values
 [1] 1.1531292 1.0889700 1.0765136 1.0248099 1.0075078 0.9926984 0.9533219
 [8] 0.9367722 0.8834080 0.8828690

$vectors
              [,1]        [,2]        [,3]        [,4]         [,5]
 [1,]  0.112436984 -0.37121765  0.47341966 -0.20738992  0.103139623
 [2,]  0.484608727  0.05575061 -0.01770245  0.32996851  0.067515555
 [3,] -0.228692064 -0.48815828  0.20308039  0.28649476  0.500656646
 [4,] -0.232490192  0.40499060  0.29262518 -0.48025212 -0.123849547
 [5,] -0.031949135  0.16118059 -0.61178243  0.08781265  0.161289155
 [6,] -0.557884289  0.24802394  0.15782882  0.25838357 -0.001868273
 [7,]  0.007055743 -0.48064664 -0.17069328 -0.39982071 -0.395600998
 [8,] -0.240054398 -0.05764926 -0.32196831 -0.47149177  0.598441643
 [9,] -0.015405949 -0.27818657 -0.32376559 -0.02988766 -0.222218221
[10,]  0.525349112  0.23988743  0.10898482 -0.27903649  0.358854999
             [,6]        [,7]        [,8]        [,9]       [,10]
 [1,] -0.07380739  0.68971166  0.07746406  0.28930807  0.03051726
 [2,]  0.27094157  0.09815149 -0.72312285  0.13720316  0.15336519
 [3,]  0.12276860 -0.09821372 -0.09707071 -0.54777825 -0.03495240
 [4,]  0.32906603  0.16989052 -0.25314902 -0.44589225  0.22420762
 [5,] -0.24956474  0.62789616 -0.01514297 -0.32785652 -0.02723450
 [6,]  0.01486085  0.14087695 -0.29134682  0.27164195 -0.59735607
 [7,] -0.29098840 -0.10511832 -0.46338991 -0.15375669 -0.29889905
 [8,]  0.09714458 -0.14690604 -0.19076435  0.40467304  0.15420830
 [9,]  0.79986315  0.15216131  0.22122246  0.04312236 -0.23139465
[10,]  0.03729309 -0.07919072  0.11141185 -0.16749641 -0.63231066

確かに第一固有値の値は1.153となり，1よりも大きな値になりました。というか，もしこのデータにカイザー基準を当てはめると，5因子もあることになってしまいます。

実際には乱数には因子など無いはずなので，平行分析では乱数で得られた固有値よりも小さい値は因子として無意味と判断します。 Rではfa.parallel()という関数があるのでやってみましょう。

コード 6.25: 平行分析

# この関数には引数corが用意されている
fa.parallel(dat[, cols], cor = "poly")

Parallel analysis suggests that the number of factors =  2  and the number of components =  2

青い線が実際のデータでの固有値を，赤い点線が乱数での固有値を表しています。（乱数を使うのでやるたびに微妙に結果が変わるかもしれませんが）Parallel analysis suggests that the number of factors = 2ということで，因子数2が提案されました²⁵。

6.11.4 累積寄与率

分散説明率の観点から言えば，共通因子によってある程度の割合は説明されていないと，「結局独自因子（よくわからないもの）で回答が決まってるんでしょ」となってしまいます。因子の数を増やせば累積寄与率は必ず上昇するので，因子数の最低条件として，累積寄与率が一定の値以上になっていない場合には因子の数を増やすというアプローチを取ることもあるようです。必要な累積寄与率の基準は一律で決まっているわけではないですが，一説によると最低50%はほしいと言われています（小杉，2018）。

6.11.5 VSS

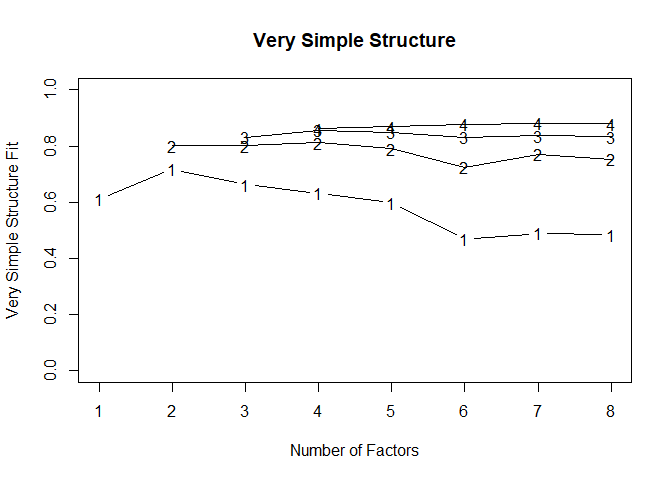
因子分析では単純構造が望ましい状態であり，なるべくこれを目指して回転が行われます。 VSS (Very Simple Structure) 基準（Revelle & Rocklin, 1979）では，得られた結果を強制的に単純構造にしたときのデータとの整合性を見ます。

完全な単純構造では，各項目は1つの因子にのみ負荷を持っているはずです，そこでVSSでは最も高い負荷を持っている因子以外の負荷をゼロにした因子負荷行列を考えます。 Section 6.7 で出したres_fa_catで言えば，表 6.5 のような状態にする，ということです。

表 6.5: 各項目が1因子のみに負荷を持つように無理やり変換

	MR2	MR1
Q1_1	0.000	0.478
Q1_2	0.000	0.743
Q1_3	0.000	0.813
Q1_4	0.000	0.486
Q1_5	0.000	0.642
Q1_6	0.617	0.000
Q1_7	0.680	0.000
Q1_8	0.580	0.000
Q1_9	0.720	0.000
Q1_10	0.603	0.000

この「無理やり単純構造にする」という操作はやや強引に感じられるかもしれませんが，例えば複数の下位尺度からなら心理尺度において，因子得点として和得点を使うということは，結果的に各項目が1因子のみに負荷している（しかも因子負荷が全て同じであるとみなしている）と仮定しているわけなので，そう考えると「よくあること」なのです（本当にそれで良いかはまた別の話）。

そして，この因子負荷行列（ $\tilde{\symbf{B}}_{\mathrm{VSS}}$ とします)に対して， $\tilde{\symbf{B}}_{\mathrm{VSS}}^\top\symbf{\Phi} \tilde{\symbf{B}}_{\mathrm{VSS}}$ によって相関行列を復元します。これをデータの相関行列 $\symbf{\Sigma}$ と比較して，差が小さければ「単純構造とみなした時にデータと整合性がある」ということになります。そこで，まず要素ごとの差 $\tilde{\symbf{B}}_{\mathrm{VSS}}^\top\symbf{\Phi} \tilde{\symbf{B}}_{\mathrm{VSS}}-\symbf{\Sigma}$ をとり，この行列の要素の二乗和を $MS_{\mathrm{VSS}}$ とします。同様に，データの相関行列 $\symbf{\Sigma}$ の要素の二乗和を $MS$ とすると， $VSS$ は $VSS = 1-\frac{MS_{\mathrm{VSS}}}{MS} \qquad(6.44)$ となります。この計算を，様々な因子数で行い，最も $VSS$ の値が小さくなったところが「単純構造として解釈した時に最もデータと整合的な因子数」ということになるわけです。

psychパッケージには，VSS()という関数が用意されています。

コード 6.26: VSS

# 引数corが用意されています
VSS(dat[, cols], cor = "poly")


Very Simple Structure
Call: vss(x = x, n = n, rotate = rotate, diagonal = diagonal, fm = fm, 
    n.obs = n.obs, plot = plot, title = title, use = use, cor = cor)
VSS complexity 1 achieves a maximimum of 0.72  with  2  factors
VSS complexity 2 achieves a maximimum of 0.81  with  2  factors

The Velicer MAP achieves a minimum of 0.04  with  2  factors 
BIC achieves a minimum of  10.65  with  5  factors
Sample Size adjusted BIC achieves a minimum of  26.53  with  5  factors

Statistics by number of factors 
  vss1 vss2   map dof   chisq    prob sqresid  fit RMSEA  BIC SABIC
1 0.61 0.00 0.059  35 2.8e+03 0.0e+00     7.1 0.61 0.180 2507  2618
2 0.72 0.80 0.035  26 5.4e+02 1.2e-97     3.6 0.80 0.090  338   421
3 0.66 0.80 0.060  18 3.1e+02 1.1e-54     3.1 0.83 0.081  168   225
4 0.63 0.81 0.084  11 1.3e+02 1.3e-22     2.5 0.86 0.067   45    80
5 0.60 0.79 0.127   5 5.0e+01 1.7e-09     2.3 0.88 0.061   11    27
6 0.47 0.73 0.186   0 1.1e+00      NA     1.9 0.89    NA   NA    NA
7 0.49 0.77 0.272  -4 5.9e-05      NA     2.0 0.89    NA   NA    NA
8 0.48 0.75 0.454  -7 1.1e-07      NA     1.9 0.89    NA   NA    NA
  complex  eChisq    SRMR eCRMS   eBIC
1     1.0 4.2e+03 1.4e-01 0.157 3937.2
2     1.1 3.7e+02 4.1e-02 0.054  164.5
3     1.2 2.1e+02 3.1e-02 0.048   64.8
4     1.4 7.8e+01 1.9e-02 0.038   -7.6
5     1.7 2.8e+01 1.1e-02 0.034  -10.7
6     1.8 4.0e-01 1.4e-03    NA     NA
7     1.9 2.2e-05 1.0e-05    NA     NA
8     1.9 4.1e-08 4.3e-07    NA     NA

complexity 1というのは， $\tilde{\symbf{B}}_{\mathrm{VSS}}$ として各項目が1つの因子のみに負荷している状態，つまり完全な単純構造を仮定した状態での結果です。同様に，各項目が上位2つの因子にのみ負荷している状態を $\tilde{\symbf{B}}_{\mathrm{VSS}}$ に仮定した場合の結果がcomplexity 2となっています²⁶。図 6.21 は各complexityにおけるVSSの値です。1の線を見ると，Number of Factorsが2のところで最も高い値になっています。これが出力されているわけです。ということでVSS(complexity 1)的には2因子が妥当だという判断がされました。

VSS()では他にも，次に示すMAPを始めとした様々な指標が出力されます。論文などで報告されることがあるものをざっと確認しましょう。

6.11.6 MAP

MAP (Minimum average partial; 最小平均偏相関) では，データの相関行列のうち共通因子の影響を取り除いた偏相関の部分に着目します。いわばこれは誤差どうしの相関であり，もしこれが全てゼロであれば，独自因子の間に別の共通因子が存在していないことになる（図 6.9 を参照）ため，因子数として妥当だと判断できます。計算自体はさほど難しくなく，まずはふつうに $k$ 因子で因子分析の初期解を求めます。つまり，データの相関行列 $\symbf{\Sigma}$ を固有値分解して，得られた固有ベクトル $\begin{bmatrix}\symbf{x}_1 & \symbf{x}_2 & \cdots & \symbf{x}_{k-1} & \symbf{x}_{k} & \symbf{x}_{k+1} & \cdots &\symbf{x}_I\end{bmatrix}$ のうち最初の $k$ 個のみを用いた $\symbf{X}_k=\begin{bmatrix}\symbf{x}_1 & \symbf{x}_2& \cdots & \symbf{x}_k\end{bmatrix}$ と，対応する $k$ 個の固有値を対角成分においた行列 $\symbf{\Lambda}_k$ を用いて $\symbf{\Sigma}$ を近似します。

$\symbf{\Sigma} \cong \symbf{X}_k\symbf{\Lambda}_k\symbf{X}_k^\top \qquad(6.45)$

そして， $\symbf{\Sigma}$ との差を取ります。 $\symbf{P} = \symbf{\Sigma} - \symbf{X}_k\symbf{\Lambda}_k\symbf{X}_k^\top \qquad(6.46)$ このとき， $\mathrm{diag}(\symbf{P})^{-\frac{1}{2}}\symbf{P}\mathrm{diag}(\symbf{P})^{-\frac{1}{2}}$ の非対角成分が， $k$ 個の共通因子の影響を取り除いた後の各変数間の偏相関係数を表します。したがって，MAPではこの非対角成分の要素の二乗の平均値を計算します。これを $k$ の数を変えて行い，最も小さいMAPを出した $k$ が妥当な因子数 $T$ だという判断ができるわけです。

6.11.7 その他

他にも，VSS()関数では次のような基準による評価を行っています。

情報量規準BICが最も小さくなる因子数
共通因子の影響を取り除いた残差相関行列に対する $\chi^2$ 統計量
モデルの適合度指標(RMSEA, SRMRなど：SEMのときに説明します)

6.11.8 最後は解釈可能性

ここまで様々な基準によって最適な因子数を推定しました。ですがその結果は一貫していません。今回の場合，多くの指標は（データの設計通り）因子数2を提示しましたが，一方で3や5といった数を出したものもあります。それぞれの指標・基準は異なる視点からの評価なので，このように結果が変わるのは当然のことです。その上で，実際に因子数を決める場合にはどうしたら良いのでしょうか。

因子分析で重要なのは，解釈可能性だと考えています。因子の名前を決める際には，分析者が自身の知識と経験をフル活用して項目の共通点をラベリングしなければいけません。そして，統計的に最適と思われる因子数が提案されたとしても，その結果は標本誤差の影響を受けている可能性がゼロとは言えません。したがって，探索的に因子数を決定する際には，

まずVSS()やfa.parallel()によって因子数にアタリをつける
提案された因子数（多くの場合はVSS()で出力されるMAPとBICの間）に関して実際に因子分析を行う
得られた結果をもとに因子の解釈を行う
最もしっくり来る解釈が得られた因子数および因子構造を採用する

という手順で行われることが多いでしょう。もしも全ての統計的な基準が指している因子数において解釈が難しいという事態に直面したら，そのときは泣いてください。

6.12 $\omega$ 係数

信頼性係数のところでは， $\alpha$ 係数はあまり良くない指標であることをお話しました。ここでは，因子分析の考え方に基づく，より良い（とされている）信頼性係数の $\omega$ 係数（McDonald, 1999）を紹介します。

6.12.1 基本的な考え方

古典的テスト理論( $x=t+e$ )における信頼性係数は $\rho=\frac{\sigma^2_t}{\sigma^2_x}=1-\frac{\sigma^2_e}{\sigma^2_x}$ という式で定義されていました。

ここで古典的テスト理論のモデルを因子分析( $\symbf{y}_i = \symbf{f}b_{i} + \symbf{\varepsilon}_i$ )に当てはめて考えてみます。真値 $t$ にあたる部分が $\symbf{f}b_{i}$ ，誤差 $e$ に当たる部分が $\symbf{\varepsilon}_i$ だと考えると，信頼性係数 $\rho$ は，観測変数 $y$ の分散のうち $\symbf{f}b_{i}$ の分散説明率になります。また，共通の因子から影響を受けている2変数の相関係数は，各変数への因子負荷の積( $b_ib_j$ )で表されました。さらに，観測変数 $y$ の共通性（＝分散説明率）は，その変数に対する因子負荷の二乗和で表されていました。これらを総合すると，各項目の因子負荷が大きいほど，内的一貫性が高いということが言えそうです。

$\omega$ 係数はこの考え方に基づき，一因子モデルであれば以下の式によって係数を求めます（ $u$ はunidimensionalの頭文字）。 $\omega_{u} = \frac{\left(\sum_{i=1}^{I}b_i\right)^2}{\sigma_{y_{total}}^2}= \frac{\left(\sum_{i=1}^{I}b_i\right)^2}{\left(\sum_{i=1}^{I}b_i\right)^2 + \sum_{i=1}^{I}\sigma_{\varepsilon_i}^2} \qquad(6.47)$ なお， $\sigma_{y_{total}}^2$ は合計点の分散を表しています。 $\omega$ 係数の基本的な考え方はこれだけなのですが，実際にはいろいろな $\omega$ を考えることができます。

Composite Reliability (CR) とAverage Variance Extracted (AVE)

（主にマーケティングの分野では？）妥当性の収束的証拠の一つとして合成信頼性 (Composite Reliability; CR)やAverage Variance Extraced (AVE)と呼ばれる指標（Bagozzi & Yi, 1988; Fornell & Larcker, 1981）が用いられているようです。これらの指標の考え方は，結局のところ $\omega$ 係数と同じで，各観測変数の分散に対して，それらの変数から抽出された共通因子による説明力の割合が大きければ，それらの変数は確かに同じ構成概念を測定しているだろう，と考えているわけです。実際に，CRの式は上で紹介した $\omega_{u}$ と全く同じです（Padilla & Divers, 2016）。

これに対してAVEは，もう少し直接的に「観測変数の分散の合計のうちどれだけの割合が共通因子で説明できるか」を求めているようです。したがって，AVEの計算式はCR（ $\omega_{u}$ ）と似て非なるものになっています。 $\begin{aligned} \mathrm{AVE} &= \frac{\sum_{i=1}^{I}b_i^2}{\sum_{i=1}^{I}b_i^2 + \sum_{i=1}^{I}\sigma_{\varepsilon_i}^2} \end{aligned} \qquad(6.48)$

考え方の違いは名前にも表れているのですが，

CR（ $\omega_{u}$ ）: 複数の観測変数の集合体 (composite) としての和得点における真値の分散説明率を考えている。複数の観測変数が集まった場合，誤差が無相関であればそれぞれ打ち消し合うことが期待されるため，変数の数が増えるほどその値は大きくなりやすい（これが因子負荷を先に全て足してから2乗するあたりに現れている）。
AVE: 観測変数一つ一つにおける平均的な真値の分散説明率を考えている。そのため観測変数が増えるほどその値は大きくなりやすいとは限らず，基本的にCRよりは低い値が出る。しかし観測変数そのものにおける信頼性を評価しているという点で，CRとは異なる価値を持っている。

という感じです。たぶん。

6.12.2 Bifactorな $\omega$

このあと登場する「$係数を計算するための関数」では，これまでとは少し異なる因子構造に基づいた計算を行っています。ということでまずはその話をしておきます。

例えば学力を考えてみると，ある科目で良い点が取れる生徒は他の科目でも良い点を取ることが多いでしょう。因子分析的に言えば，これは全ての科目が一つの因子の影響を受けている，という見方が出来ます。ですが，果たして国語と数学と英語と…様々な科目の学力をたったひとつの因子で説明できるのでしょうか。図 6.22 のように，特に知能などを扱う領域では「総合的なもの」であるG因子と，特定の項目にのみ影響を与える因子（群因子と呼んだりする）がそれぞれ存在するという双因子(Bifactor)モデルというものを考えることがあります。

双因子モデルに基づけば，観測変数はG因子による部分が追加されて $\symbf{y}_i = \symbf{g}b^g_{i} + \symbf{f}b_{i} + \symbf{\varepsilon}_i \qquad(6.49)$ となります。こうなると，「信頼性」に複数の解釈が生まれます。

まず，図 6.22 の5科目のテストに共通している部分のみ（全体としての内的一貫性）を考えると，これはG因子による分散説明率のみを取り上げる必要があります。したがって， $\omega_{h} = \frac{\left(\sum_{i=1}^{I}b^g_{i}\right)^2}{\sigma_{y_{total}}^2} \qquad(6.50)$ という $\omega$ 係数が考えられます( $h$ はhierarchicalの頭文字)。

一方で，特定の項目にのみ影響を与えるものを含めた「共通因子によって説明可能な部分」（どちらかというと元の信頼性の定義に近い）を考えると， $\omega_{t} = \frac{\left(\sum_{i=1}^{I}b^g_{i}\right)^2 + \left(\sum_{i=1}^{I}b_i\right)^2}{\sigma_{y_{total}}^2} \qquad(6.51)$ という $\omega$ 係数が考えられます（ $t$ はtotalの頭文字）。

どの $\omega$ 係数も間違いではありません。ただ視点が異なるだけなのです。その上でどのように使い分けるかですが，これは仮説での因子構造によります （Flora, 2020）。心理尺度を作成する場合には，尺度全体として一つの構成概念を反映していると考えるでしょう。もし一因子性が満たされている場合には，最初に紹介した $\omega_u$ を用いるのが良いでしょう。

もし

因子構造として多因子を仮定しているが，尺度得点としては全項目の合計点を利用しようと考えている場合
もともと一因子で尺度を作ろうとしていたけれども結果的に一因子性が満たされなくなってしまった場合

には，適切な因子構造のもとで $\omega$ を計算する必要があります。つまり特定の項目にのみ影響を与える因子に加えてG因子に相当するものを用意し，このG因子の分散説明率をもって尺度全体の内的一貫性を求めるべき，ということで $\omega_h$ を使用すべきかもしれません。

なお，尺度の内的一貫性という観点で言えば， $\omega_t$ を使うことは基本的には無いと思っていてよい気がします。

psych::omega()という関数は， $\omega$ 係数を求めることができる関数です。

コード 6.27:

\omega_u

を求める

# 引数poly=TRUEにするとポリコリック相関でやってくれる
omega(dat[, cols], nfactors = 1, poly = TRUE)

Warning in schmid(m, nfactors, fm, digits, rotate = rotate, n.obs = n.obs,
: Omega_h and Omega_asymptotic are not meaningful with one factor

Omega 
Call: omegah(m = m, nfactors = nfactors, fm = fm, key = key, flip = flip, 
    digits = digits, title = title, sl = sl, labels = labels, 
    plot = plot, n.obs = n.obs, rotate = rotate, Phi = Phi, option = option, 
    covar = covar)
Alpha:                 0.78 
G.6:                   0.81 
Omega Hierarchical:    0.79 
Omega H asymptotic:    1 
Omega Total            0.78 

Schmid Leiman Factor loadings greater than  0.2 
         g  F1*   h2   h2   u2 p2 com
Q1_1  0.31           0.09 0.91  1   1
Q1_2  0.57      0.33 0.33 0.67  1   1
Q1_3  0.59      0.35 0.35 0.65  1   1
Q1_4  0.54      0.29 0.29 0.71  1   1
Q1_5  0.54      0.29 0.29 0.71  1   1
Q1_6  0.46      0.21 0.21 0.79  1   1
Q1_7  0.52      0.27 0.27 0.73  1   1
Q1_8  0.49      0.24 0.24 0.76  1   1
Q1_9  0.58      0.34 0.34 0.66  1   1
Q1_10 0.54      0.30 0.30 0.70  1   1

With Sums of squares  of:
   g  F1*   h2 
2.72 0.00 0.79 

general/max  3.44   max/min =   9.493814e+15
mean percent general =  1    with sd =  0 and cv of  0 
Explained Common Variance of the general factor =  1 

The degrees of freedom are 35  and the fit is  1.15 
The number of observations was  2432  with Chi Square =  2779.53  with prob <  0
The root mean square of the residuals is  0.14 
The df corrected root mean square of the residuals is  0.16
RMSEA index =  0.18  and the 90 % confidence intervals are  0.174 0.185
BIC =  2506.65

Compare this with the adequacy of just a general factor and no group factors
The degrees of freedom for just the general factor are 35  and the fit is  1.15 
The number of observations was  2432  with Chi Square =  2779.53  with prob <  0
The root mean square of the residuals is  0.14 
The df corrected root mean square of the residuals is  0.16 

RMSEA index =  0.18  and the 90 % confidence intervals are  0.174 0.185
BIC =  2506.65 

Measures of factor score adequacy             
                                                 g F1*
Correlation of scores with factors            0.89   0
Multiple R square of scores with factors      0.79   0
Minimum correlation of factor score estimates 0.59  -1

 Total, General and Subset omega for each subset
                                                 g  F1*
Omega total for total scores and subscales    0.78 0.79
Omega general for total scores and subscales  0.79 0.79
Omega group for total scores and subscales    0.00 0.00

引数nfactorsは，G因子以外の共通因子の数を指定します。 nfactors=1にした場合，G因子との識別性を失うため，実質的に1因子（G因子のみ）での因子分析を行っているのと同じ状態になります。デフォルトではnfactors=3となっていますが，この設定で計算した場合，実質4因子（G因子に加えて3つの共通因子）で因子分析を行うことになります。その結果，G因子のみを考慮する $\omega_h$ では過小推定してしまい，一方 $\omega_t$ では因子数が多すぎて過大推定になってしまいがちなようです（岡田，2011）。

出力を見てみましょう。

Alpha:                 0.78 
G.6:                   0.81 
Omega Hierarchical:    0.79 
Omega H asymptotic:    1 
Omega Total            0.78

一番上にはalpha()関数と同じように $\alpha$ 係数およびG6を出してくれています。その下に続いているのが $\omega_h$ (omega hierarchical)です。報告する際にはこの値を示せばOKです。その下にあるOmega H asymptoticは，「項目数が無限にあったら」，つまり「独自因子の影響を無視できたら」という状況での $\omega_h$ 係数なので報告の必要がありません。最後には $\omega_t$ 係数が表示されています。nfactors=1のときには $\omega_h$ と同じ値になります²⁷。

Schmid Leiman Factor loadings greater than  0.2 
         g  F1*   h2   h2   u2 p2 com
Q1_1  0.31           0.09 0.91  1   1
Q1_2  0.57      0.33 0.33 0.67  1   1
Q1_3  0.59      0.35 0.35 0.65  1   1

（以下略）

因子負荷行列です。nfactors=1の場合，G因子のみでの因子分析の結果になります。fa(dat[,cols],nfactors=1)と同じ値が出ているはずです。

今回は，最初に作成したcolsに含まれる10項目でomega()を実行しましたが，この10項目は2因子ぶんの項目になっています。続いて2因子にして結果を見比べてみましょう。

コード 6.28: 2因子だとどうなるの

omega(dat[, cols], nfactors = 2, poly = TRUE)

Omega 
Call: omegah(m = m, nfactors = nfactors, fm = fm, key = key, flip = flip, 
    digits = digits, title = title, sl = sl, labels = labels, 
    plot = plot, n.obs = n.obs, rotate = rotate, Phi = Phi, option = option, 
    covar = covar)
Alpha:                 0.78 
G.6:                   0.81 
Omega Hierarchical:    0.42 
Omega H asymptotic:    0.51 
Omega Total            0.83 

Schmid Leiman Factor loadings greater than  0.2 
         g   F1*   F2*   h2   h2   u2   p2  com
Q1_1  0.22        0.39 0.21 0.21 0.79 0.24 1.70
Q1_2  0.43        0.60 0.55 0.55 0.45 0.34 1.82
Q1_3  0.46        0.66 0.65 0.65 0.35 0.33 1.79
Q1_4  0.38        0.39 0.32 0.32 0.68 0.45 2.22
Q1_5  0.40        0.52 0.43 0.43 0.57 0.37 1.88
Q1_6  0.33  0.50       0.36 0.36 0.64 0.31 1.76
Q1_7  0.38  0.55       0.45 0.45 0.55 0.32 1.78
Q1_8  0.35  0.47       0.35 0.35 0.65 0.36 1.85
Q1_9  0.43  0.58       0.53 0.53 0.47 0.35 1.84
Q1_10 0.39  0.49       0.39 0.39 0.61 0.38 1.93

With Sums of squares  of:
  g F1* F2*  h2 
1.5 1.4 1.4 1.9 

general/max  0.76   max/min =   1.4
mean percent general =  0.34    with sd =  0.05 and cv of  0.16 
Explained Common Variance of the general factor =  0.35 

The degrees of freedom are 26  and the fit is  0.22 
The number of observations was  2432  with Chi Square =  540.84  with prob <  1.2e-97
The root mean square of the residuals is  0.04 
The df corrected root mean square of the residuals is  0.05
RMSEA index =  0.09  and the 90 % confidence intervals are  0.084 0.097
BIC =  338.13

Compare this with the adequacy of just a general factor and no group factors
The degrees of freedom for just the general factor are 35  and the fit is  1.35 
The number of observations was  2432  with Chi Square =  3282.92  with prob <  0
The root mean square of the residuals is  0.19 
The df corrected root mean square of the residuals is  0.21 

RMSEA index =  0.195  and the 90 % confidence intervals are  0.19 0.201
BIC =  3010.05 

Measures of factor score adequacy             
                                                  g  F1*  F2*
Correlation of scores with factors             0.66 0.75 0.76
Multiple R square of scores with factors       0.43 0.56 0.58
Minimum correlation of factor score estimates -0.14 0.12 0.16

 Total, General and Subset omega for each subset
                                                 g  F1*  F2*
Omega total for total scores and subscales    0.83 0.78 0.78
Omega general for total scores and subscales  0.42 0.27 0.28
Omega group for total scores and subscales    0.39 0.51 0.51

先ほどとは打って変わって，Omega Hierarchicalの値がかなり低下しました。データがかなりきれいに2因子に分かれているため，「すべてに共通の1因子(G因子)」の影響がかなり弱いことがわかります。このような状態では，10項目の合計点の内的一貫性は低い，という判断になるわけです。このように， $\omega_h$ では内的一貫性だけでなく「一因子性」も評価してあげることが出来ている感じがします。

omega()関数では，デフォルトで図 6.23 のようなプロットを出してくれます。 F1およびF2に関しては，因子分析を行った結果をもとに，勝手に最適なグルーピングをしてくれているわけです。ボトムアップに尺度を作成するような場面では，fa()の結果に基づくこのやり方で $\omega_h$ を求めるのが良いでしょう。一方で，もともと因子構造の仮定があるような場合は，omega()関数は勝手にグループを決定してしまうので使えません。そのような場合には，次回とりあげるSEMの枠組み（lavaanパッケージ）で $\omega_h$ を計算しましょう。

omega()関数におけるG因子の話

まず，そもそもなぜomega()関数では頼んでもいないのにG因子なるものを入れて計算しているのかといえば，これは単に McDonald （1978）が $\omega$ 係数を最初に提案したときに「bifactorモデルにおけるG因子の分散説明率」として定義したためだと思われます。いわば， $\omega$ 係数はそもそもbifactorモデルのために作られた指標，ということなのでしょう。

ということでG因子の存在は諦めるとして，以下では「G因子と共通因子はどのように区別して推定されるのか」という少しテクニカルな話を記しておきます（Reise, 2012）。

図 6.22 に示されているように，G因子はほかの共通因子とは無相関であるというところが重要なポイントです。つまり，共通因子数を $T$ （nfactors=T）にした場合には， $(T+1)\times I$ 因子負荷行列が

1列目は2列目以降と全て直交（G因子）
2列目以降は1列目と直交さえしていればそれ以外とは直交していなくてもよい（共通因子）

という条件を満たすように因子負荷行列が推定されるのです。実際にomega()関数の中で行われている手順は，

普通に $T$ 因子解を求める
斜交回転する
Schmid-Leiman変換（Schmid & Leiman, 1957）を行う

という流れです。 Schmid-Leiman変換は，bifactorモデルのために考案された「普通の因子負荷行列からbifactorモデルの因子負荷行列に簡単に変換できる方法」です。これによって，手順2. で求めた因子負荷行列は，1列追加されるとともに，1列目が2列目以降と直交する形に変換されるのです。

6.13 主成分分析との違い

因子分析は，よく主成分分析と対比される手法です。ここで少しだけその違いを説明しておきましょう。

主成分分析の主目的は，次元圧縮です。これは，複数の変数を合体させて最も高い説明力を持つ「最強の変数」を作るようなイメージです。グラフィカルモデル的には図 6.24 のようになります。因子分析モデル（図 6.4 ）と比べると，矢印の向きが逆になっているわけです。

そして，主成分分析ではとにかく「なるべく分散説明率の高い主成分を作る」ことで「なるべく少ない数の変数にまとめる」ことが重要となります。そのため，全ての項目間に正の相関がある場合には，基本的に第一主成分に対しては全ての項目が高い負荷量を示すと考えられます²⁸。これと比べると，因子分析では項目をいくつかのグループに分ける意識が強いと言えます。そのため，因子数は最小限というよりも「メリハリのある分かれ方（＝単純構造）をする数」になるように設定されることが多いです。

また，数理的には主成分分析では誤差を想定しないという違いがあります。なので図 6.24 においても，これに誤差項（独自因子）を追加することはありません。もう少し具体的に説明しましょう。因子分析（主因子法）では，観測変数の相関行列 $\symbf{\Sigma}$ を $\symbf{B}^\top\symbf{B} + \symbf{\Psi}$ と分解した上で， $\symbf{B}^\top \symbf{B}$ の部分に対して固有値分解を行うことで因子負荷量を計算していました。これに対して主成分分析では $\symbf{\Sigma}$ そのものを固有値分解したものが主成分負荷量になります。主成分分析のほうが $\symbf{\Psi}$ のぶんだけ大きな値の行列を固有値分解するため，得られる固有値も大きな値になります。

Rのpsychパッケージでは，pca()という関数で行うことが出来ます。固有値分解の結果と見比べてみましょう。

コード 6.29: 固有値分解

eig <- eigen(cor(dat[, cols]))
# 主成分負荷量は固有ベクトルに固有値の平方根をかけた値になる
eig$vectors[, 1] * sqrt(eig$values[1])

 [1] -0.3240019 -0.5916129 -0.6105479 -0.5661146 -0.5645371 -0.5047118
 [7] -0.5737352 -0.5470221 -0.6143070 -0.5920611

コード 6.30: 主成分分析

# デフォルトではバリマックス回転してしまうので，引数rotateを指定する
pca(dat[, cols], nfactors = 2, rotate = "none")

Principal Components Analysis
Call: principal(r = r, nfactors = nfactors, residuals = residuals, 
    rotate = rotate, n.obs = n.obs, covar = covar, scores = scores, 
    missing = missing, impute = impute, oblique.scores = oblique.scores, 
    method = method, use = use, cor = cor, correct = 0.5, weight = NULL)
Standardized loadings (pattern matrix) based upon correlation matrix
       PC1   PC2   h2   u2 com
Q1_1  0.32  0.46 0.32 0.68 1.8
Q1_2  0.59  0.49 0.59 0.41 1.9
Q1_3  0.61  0.52 0.64 0.36 1.9
Q1_4  0.57  0.28 0.40 0.60 1.5
Q1_5  0.56  0.44 0.51 0.49 1.9
Q1_6  0.50 -0.45 0.46 0.54 2.0
Q1_7  0.57 -0.44 0.53 0.47 1.9
Q1_8  0.55 -0.38 0.45 0.55 1.8
Q1_9  0.61 -0.42 0.56 0.44 1.8
Q1_10 0.59 -0.35 0.47 0.53 1.6

                       PC1  PC2
SS loadings           3.08 1.83
Proportion Var        0.31 0.18
Cumulative Var        0.31 0.49
Proportion Explained  0.63 0.37
Cumulative Proportion 0.63 1.00

Mean item complexity =  1.8
Test of the hypothesis that 2 components are sufficient.

The root mean square of the residuals (RMSR) is  0.09 
 with the empirical chi square  1871.22  with prob <  0 

Fit based upon off diagonal values = 0.88

PC1列は符号こそ異なりますが，データの相関行列をそのまま固有値分解した結果と一致する値が得られています。

Bagozzi, R. P., & Yi, Y. (1988). On the evaluation of structural equation models. Journal of the Academy of Marketing Science, 16(1), 74–94. https://doi.org/10.1007/BF02723327

Bartlett, M. S. (1950). Tests of significance in factor analysis. British Journal of Statistical Psychology, 3(2), 77–85. https://doi.org/10.1111/j.2044-8317.1950.tb00285.x

Bartlett, M. S. (1951). The effect of standardization on a χ2 approximation in factor analysis. Biometrika, 38(3/4), 337–344. https://doi.org/10.2307/2332580

Browne, M. W. (1968). A comparison of factor analytic techniques. Psychometrika, 33(3), 267–334. https://doi.org/10.1007/BF02289327

Browne, M. W. (2001). An overview of analytic rotation in exploratory factor analysis. Multivariate Behavioral Research, 36(1), 111–150. https://doi.org/10.1207/S15327906MBR3601_05

Cliff, N. (1988). The eigenvalues-greater-than-one rule and the reliability of components. Psychological Bulletin, 103(2), 276–279. https://doi.org/10.1037/0033-2909.103.2.276

Flora, D. B. (2020). Your coefficient alpha is probably wrong, but which coefficient omega is right? A tutorial on using R to obtain better reliability estimates. Advances in Methods and Practices in Psychological Science, 3(4), 484–501. https://doi.org/10.1177/2515245920951747

Fornell, C., & Larcker, D. F. (1981). Evaluating structural equation models with unobservable variables and measurement error. Journal of Marketing Research, 18(1), 39–50. https://doi.org/10.2307/3151312

Guttman, L. (1953). Image theory for the structure of quantitative variates. Psychometrika, 18(4), 277–296. https://doi.org/10.1007/BF02289264

萩生田伸子・繁桝算男（1996）．順序付きカテゴリカルデータへの因子分析の適用に関するいくつかの注意点　心理学研究，67(1), 1–8. https://doi.org/10.4992/jjpsy.67.1

林邦好・冨田誠・田中豊（2008）．主成分分析における軸の回転について　計算機統計学，19(2), 89–101. https://doi.org/10.20551/jscswabun.19.2_89

堀一輝・牧野直道（2024）．測定モデルユーザーのための次元性評価法総論　日本テスト学会誌，20, 135–167. https://doi.org/10.24690/jart.20.1_135

堀啓造（2005）．因子分析における因子数決定法――並行分析を中心にして――　香川大学経済論叢，77(4), 35–70.

Kaiser, H. F. (1970). A second generation little jiffy. Psychometrika, 35(4), 401–415. https://doi.org/10.1007/BF02291817

Kaiser, H. F. (1974). An index of factorial simplicity. Psychometrika, 39(1), 31–36. https://doi.org/10.1007/BF02291575

Kaiser, H. F. (1981). A revised measure of sampling adequacy for factor-analytic data matrices. Educational and Psychological Measurement, 41(2), 379–381. https://doi.org/10.1177/001316448104100216

Kaiser, H. F., & Rice, J. (1974). Little jiffy, mark IV. Educational and Psychological Measurement, 34(1), 111–117. https://doi.org/10.1177/001316447403400115

Kiers, H. A. L., & Ten Berge, J. M. F. (1994). The Harris-Kaiser independent cluster rotation as a method for rotation to simple component weights. Psychometrika, 59(1), 81–90. https://doi.org/10.1007/BF02294267

小杉考司（2018）．言葉と数式で理解する多変量解析入門　北大路書房

McDonald, R. P. (1978). Generalizability in factorable domains: “domain validity and generalizability.” Educational and Psychological Measurement, 38(1), 75–79. https://doi.org/10.1177/001316447803800111

McDonald, R. P. (1999). Test theory: a unified treatment (0th ed.). Psychology Press. https://doi.org/10.4324/9781410601087

岡田謙介（2011）．クロンバックのαに代わる信頼性の推定法について――構造方程式モデリングによる方法・McDonaldのωの比較――　日本テスト学会誌，7, 37–50. https://doi.org/10.24690/jart.7.1_37

Padilla, M. A., & Divers, J. (2016). A comparison of composite reliability estimators: coefficient omega confidence intervals in the current literature. Educational and Psychological Measurement, 76(3), 436–453. https://doi.org/10.1177/0013164415593776

Reise, S. P. (2012). The rediscovery of bifactor measurement models. Multivariate Behavioral Research, 47(5), 667–696. https://doi.org/10.1080/00273171.2012.715555

Revelle, W., & Rocklin, T. (1979). Very simple structure: an alternative procedure for estimating the optimal number of interpretable factors. Multivariate Behavioral Research, 14(4), 403–414. https://doi.org/10.1207/s15327906mbr1404_2

Schmid, J., & Leiman, J. M. (1957). The development of hierarchical factor solutions. Psychometrika, 22(1), 53–61. https://doi.org/10.1007/BF02289209

Shirkey, E. C., & Dziuban, C. D. (1976). A note on some sampling characteristics of the measure of sampling adequacy (MSA). Multivariate Behavioral Research, 11(1), 125–128. https://doi.org/10.1207/s15327906mbr1101_9

Thurstone, L. L. (1947). Multiple-factor analysis: a development and expansion of the vectors of mind. University of Chicago Press.

Zwick, W. R., & Velicer, W. F. (1986). Comparison of five rules for determining the number of components to retain. Psychological Bulletin, 99(3), 432–442. https://doi.org/10.1037/0033-2909.99.3.432

英語の25項目は?psych::bfiから確認することができます。また日本語訳はIPIPプロジェクト内にある翻訳の情報から拝借しました。↩︎
因子分析モデルの制約は，正確に言うと「パラメータが一つ固定されていれば良い」ので，別の制約として第1項目の因子負荷を1に固定するという方法を取ることもあります。↩︎
回帰分析において説明変数・観測変数ともに標準化されている場合，切片項はゼロになります。これが，「因子分析は結局回帰分析だ」と言っておきながら(6.1)および(6.2)式に切片項がなかった理由です。↩︎
MRというのは，因子負荷行列を最小残差法(Minimum Residual)で計算したことを表しています。詳細は Section 6.10 にて説明します。↩︎
ちなみに3因子以上の場合，fa.plot()は各因子ペアごとの散布図を並べてくれます。↩︎
加えて，実はSEMの数理的には1因子には3項目以上あることが望ましかったりもします。↩︎
「共通因子間の相関もゼロ」という3行目の仮定は，図 6.5 において $f_1$ と $f_2$ の間に直接的なパスが無いことに相当します。↩︎
厳密には，ここで近似しているのは $\symbf{\Sigma} - \symbf{\Psi} = \symbf{b}^\top\symbf{b}$ です。しかし実際には $\symbf{\Psi}$ はわからないので，計算上は「対角成分を $\symbf{\Psi}$ に置き換えた $\symbf{\Sigma}$ 」について固有値分解を繰り返すことで，「非対角成分だけ近似された状態」を求めます。なので上の近似も対角成分（全て1になるはず）はあまりうまく近似されていません。↩︎
ここで紹介しているのは画像処理における次元圧縮のマネです。↩︎
回転前後で共通性の値は変わらないため，h2の値は回転前の初期解の因子負荷の二乗和には一致します。回転して因子間相関を持ったことで，各因子の影響のうち僅かな部分が別の因子を経由したものに置き換わったというイメージです。↩︎
項目の共通性は，因子負荷行列 $\symbf{B}$ を列（項目）ごとに二乗和したもの $\mathrm{diag}(\tilde{\symbf{B}}\symbf{\Phi}\tilde{\symbf{B}}^\top)$ でした。それに対して因子寄与率は因子負荷行列を行（因子）ごとに二乗和しているため， $\mathrm{diag}(\tilde{\symbf{B}}^\top\symbf{\Phi}\tilde{\symbf{B}})$ という順番になっているのです。↩︎
「合計点の分散」ではなく「分散の合計」です。なので観測変数間の相関などは気にする必要はありません。↩︎
一説には，50%くらいの累積寄与率はほしいという声もあったりするそうです。↩︎
尺度としての使いやすさや計算の簡便性を考えると合計点を使うのはありなのですが，個人的には例えば尺度得点として重み付け和を使う，みたいな方法はもっと広まっても良いのでは，と思っています。↩︎
polycorパッケージにあるhetcor()関数は，データフレームに対してポリコリック・ポリシリアル・ピアソンの相関行列を出してくれる関数です。ただこの関数では，データフレームの各列がカテゴリカルであるかを自動的に判別して，変数のペアごとに適切な相関を算出します。したがって，この関数を使う場合は事前にカテゴリカル変数の型をas.factor()等で変換する必要があります。↩︎
細かい話をすると，fa()関数にデータフレームを与えた場合，相関係数の計算時にはuse="pairwise.complete.obs"が指定されていることになります。そのため，もしも欠測値の無いデータのみで因子分析をしたい場合には，事前にuse="complete.obs"で相関行列を計算して与える，という使い方もできます。もっというとfa()関数自体が引数useを受け付けるのですが。↩︎
どうやらSPSSではこの後紹介する分析の結果がデフォルトで出てくるようです。一方でここで紹介している分析を（SPSS以外で分析をする人が）論文にも書かなかったとしても咎められる可能性は高くないので「出来そうならやってみてもいいんじゃないかなぁ」くらいの位置づけとして紹介します。↩︎
これは，アダマールの不等式というものによって証明される性質です。↩︎
実際に私はSPSSを使わないので，ここに来て修士論文の審査をするまでこの検定の存在を知りませんでした。↩︎
こんなことになっている原因として考えられるのは，KMOには複数の定義があり，取りうる値の範囲が異なること（Kaiser, 1981），表に示された基準が厳密にはKMOに関するものではない（単純構造の程度に関するものである）こと，などがありそうですがよく分かりません。↩︎
名前の由来はギリシャ神話に登場するプロクルーステスのベッドです。↩︎
fa()関数では，直交回転（clusterT）と斜交回転（clusterQ）を両方選ぶことが出来ます。clusterと指定した場合は斜交回転になります。↩︎
オブリミン回転は，コーティミン回転やコバリミン回転などの回転法を一般化したものなので，コーティミン回転はオブリミン回転の特殊なケースなのです。↩︎
fa()関数では，直交ジオミン回転（geominT）と斜交ジオミン回転（geominQ）を両方選ぶことが出来ます。↩︎
ここでもnumber of componentsは主成分分析の話なので無視してOKです。↩︎
一応内部的にはcomplexity 8まで計算されていますが，それはもう単純構造では無いのでは？という気がするので大抵の場合はcomplexity 2くらいまで見ておけば十分でしょう。↩︎
nfactors=1のときにはG因子と共通因子を識別できないので， $\omega_t$ のほうもG因子のみで推定を行っています。そのために2つは同じ値になるのです。↩︎
ただ，主成分の解釈をしようと考えるケースもあるらしく，その場合には主成分軸の回転をすることもあります（林他，2008）。ただしこの場合得られる得点は「なるべく分散説明率の高い」を追求した得点ではないため，厳密には主成分分析ではなくなる，という見方もあるようです。↩︎