統計を学ぶ人の大多数が最初に出会う「多変量解析」は，きっと（重）回帰分析でしょう。 実際に，後半で登場する因子分析・構造方程式モデリング・項目反応理論はいずれも回帰分析のモデルと関係のあるモデルです。 一応本講義では回帰分析については既習であることを前提としているので，基本的な回帰分析のおさらいをはさみ，後半の内容に必要な部分だけでも前提知識を補いたいと思います。 なお，このChapterでは，基本的に今後紹介する手法の理解に必要・重要と思われる内容に絞って紹介しています。 回帰分析は相当幅広く用いられているため，本気を出せば回帰分析だけで1コマ15回の講義を余裕で組めると思います。 回帰分析を深く理解したい方は，恐縮ながら経済学研究科や国際協力研究科などで開講されている講義も探してみてください。
5.1 回帰分析とは
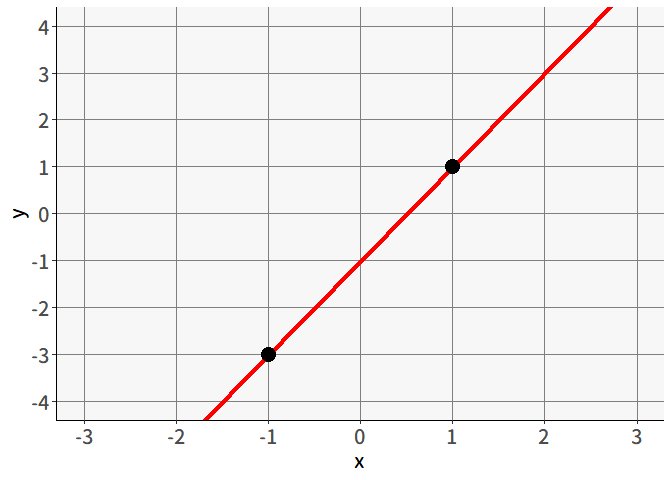
中学数学では， 図 5.1 のように「2つの点を通る直線を求める」問題を解いたことがあると思います。回帰分析はこの延長にある分析手法と言っても良いでしょう。
この問題を（今後の問題設定に合わせて）数式を用いて表現すると，
と言った感じでしょうか。 なお，これ以降は一つ一つのデータ（行方向）を表すために，回答者(person)の頭文字をとって添字\(p\)をつけることにします。 つまり，\((x_p,y_p)=(-1,-3), (1,1)\)は丁寧に書くと\((x_1,y_1)=(-1,-3), (x_2,y_2)=(1,1)\)となり，それぞれ1人目，2人目の変数\(x,y\)の値を表しているとします。
さて，先程の書き方をもう少し変えてみると，
と表すこともできるでしょう。 そして 図 5.1 の場合，正解は\((b_0,b_1)=(-1,2)\)となり，一次関数で表せば\(y=-1+2x\)となります。
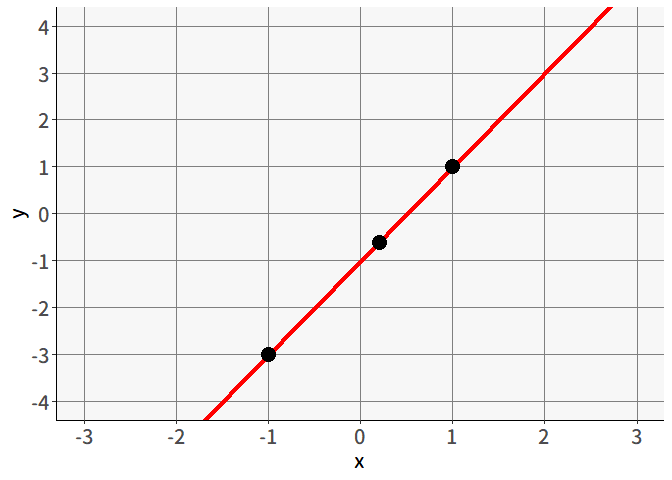
ここまでは2つの点のみについて考えてきましたが，点の数が増えたらどうでしょうか。 図 5.2 のように，「3つの点を通る直線を求める」問題があったとしても，すべての点が一直線上に並んでいるなら一つの答えを出すことができます。このケースでも，正解は\(y=-1+2x\)ですね。
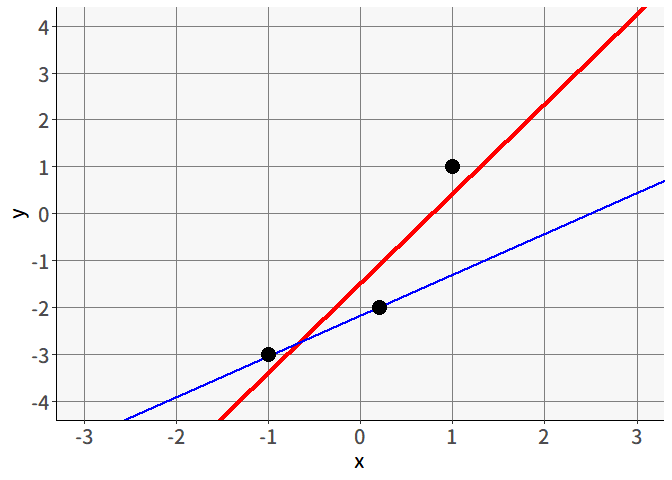
では， 図 5.3 のように3つの点が一直線上に並んでいない場合は？当然ながらすべての点を通る直線は存在しません。回帰分析の問題設定はこういった状況です。すべての点を通らないならばそれなりに最もそれっぽい直線を何らかの方法で決定して引いてあげる必要があります。
どんな線が最もそれっぽい直線かですが， 図 5.3 の赤い線と青い線を比較すると，ほとんどの人は赤い線のほうがそれっぽいと感じるのではないでしょうか。青い線の方は，3つのうち2つの点を通過しているにも関わらず，なぜか赤い線のほうがそれっぽいですね。これは，赤い線のほうが平均的にはズレが小さいためです。確かに青い線は，通過している2つの点に関してはズレがゼロですが，残り1個の点に対しては大きくズレています。この赤い線のように，平均的なズレを最小化する直線を求める分析法が回帰分析なのです。
点の数が何個であろうと最もベーシックな回帰分析では，直線（一次関数）を求めます。傾きを\(b_1\)，切片を\(b_0\)とおけば \[ y=b_0 + b_1x \tag{5.1}\] という直線について，\(b_0,b_1\)の値がいくつのときに最もそれっぽい直線になるかを求めるわけです。
5.1.1 最小二乗法
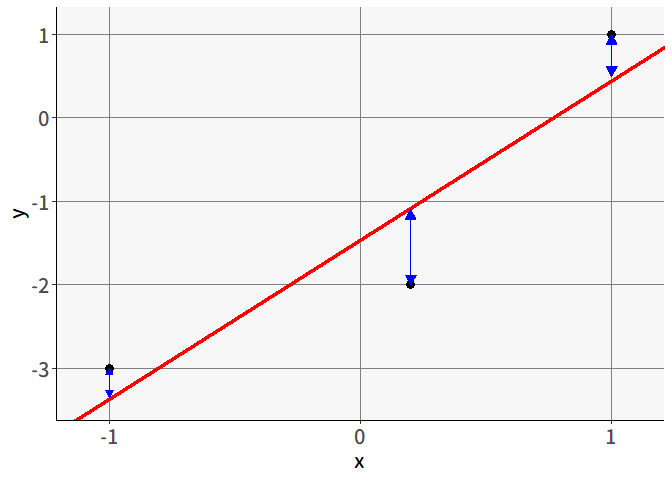
実際の分析においては，最小二乗法によって回帰直線を求めることが多いです。これは 図 5.4 の青い矢印のように，縦方向でのズレを求めて，これの二乗和が最小になる\((b_1, b_0)\)の組み合わせを求める方法です。
「それっぽい直線」という観点で言えば， 図 5.5 の青い矢印のように，赤い直線との直線距離に関して最小化しても良さそうな気がしますが，最小二乗法では縦方向での距離を最小化しています。なぜなのでしょうか。
それは，回帰分析が\(x\)で\(y\)を説明する分析手法だからです。\(y\)そのものは無いけれど他の変数がある時に\(y\)を近似するのが回帰直線なのです。 例えば，\(x\)を「体重」，\(y\)を「身長」だとしましょう。あなたのもとに，あるゲストがやってきます。どういうわけかその人に関して「体重」の情報だけが入っているとします。あなたはゲストのためにちょうどよい高さの椅子を用意する必要があります。しかし，ちょうどよい高さの椅子をあてがうためには，ゲストの身長が分かっていないといけません1。さて，あなたはゲストの身長をどのように見積もるでしょうか。
普通ならば， 図 5.6 のように，周りの人の体型などから「（標準体型で）体重が70kgくらいの人ならば，身長はだいたい170cmくらい」「（標準体型で）体重が60kgくらいの人ならば，身長はだいたい162cmくらい」という感じで予測を立てたうえで，ゲストの体重の情報を当てはめて「ゲストの体重が65kgということは，標準体型ならば身長はだいたい165.5mくらいかなぁ」といった予測を行うでしょう。 回帰分析で行っていることは概ねこんな感じのことですが，ここで問題になる「予測のズレ」は，身長（つまり\(y\)）に関してのみです。 つまり，\(x\)による\(y\)の近似（予測）のズレが最小になるように回帰直線を引きたいがために，最小二乗法では縦方向でのズレのみを考えているわけですね。
求めたい回帰直線は\(y=b_0 + b_1x\)ですが，一つ一つの点について考えると，ほとんどの場合等号は成立しません。 というのも回帰直線が示すのはあくまでも予測値であって，実際のデータでは予測とのズレがあるためです。 そこで回帰分析モデルでは，実際の一つ一つのデータの値\(y_p\)は，回帰直線による予測値\(\widehat{y_p}\)と誤差\(\varepsilon_p\)の和であると考えます。 ということで，回帰分析モデルの全体は \[ \begin{aligned} y_p &= \widehat{y_p} + \varepsilon_p \\ \widehat{y_p} &= b_0 + b_1x_p \\ \varepsilon_p &\sim N(0,\sigma_{\varepsilon}^2) \end{aligned} \tag{5.2}\] となり，\(P\)をデータの総数とすると，最小二乗法では \[ \sum_{p=1}^{P}(y_p-\widehat{y_p})^2 = \sum_{p=1}^{P}\left[y_p-(b_0 + b_1x_p)\right]^2 \tag{5.3}\] を最小化するような\((b_0, b_1)\)の組み合わせを求めている，というわけです。
最尤法
最小二乗法と同じくらい用いられる推定法が最尤法です。(5.2)式の回帰分析モデルの式を変形させると， \[ y_p \sim N(b_0 + b_1x_p, \sigma_{\varepsilon}^2) \tag{5.4}\] という形にもなります。したがって，データから最も尤度が大きくなる\((b_0, b_1, \sigma_{\varepsilon})\)の組を見つけてあげることで，回帰直線を最尤推定することも可能なわけです。
最小二乗法とどちらが良いかという話ではなく，最適化の目的関数が異なるということなので，回帰直線を求める方法は最小二乗法だけじゃないということは頭の片隅に入れておいても良い知識だと思います。
5.1.2 （単）回帰分析の線形代数的表現
因子分析やSEMのところでは，それぞれの分析手法の基本的な考え方を説明するために線形代数的表現を多用しています。 ということで，ここで回帰分析の線形代数による表現を説明しておきます。 書き方とその意味に慣れておいてください。
まず，回帰分析モデルを， 図 5.1 のところで示した連立方程式的な書き方で書き直すと，次のようになります。
毎回全部式を書いていると面倒なので，ここで線形代数の力を借ります。 連立方程式のうち，すべての式に共通しているのが\(b_0,b_1\)の部分です。 一旦ここはそのままにしておいて，その他の（\(p\)ごとに異なる）部分をベクトルでまとめて書き直してみます。
\[ \left\{ \begin{aligned} \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_{P-1} \\ y_P \end{bmatrix} = b_0\begin{bmatrix} 1 \\ 1 \\ \vdots \\ 1 \\ 1 \end{bmatrix} + b_1 \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_{P-1} \\ x_P \end{bmatrix} + \begin{bmatrix} \varepsilon_1 \\ \varepsilon_2 \\ \vdots \\ \varepsilon_{P-1} \\ \varepsilon_P \end{bmatrix} \end{aligned}\right. \tag{5.5}\] なお切片\(b_0\)には，ベクトル同士の足し算を成立させるために\(P\)人分の1が並んだベクトル（以後太字の\(\symbf{1}\)と表記する）をかけています。
だいぶ見通しが良くなってきました。あとはベクトルを太字で表すことで，以下のように割と綺麗に書き直すことが出来ます。
ということで，これでデータが何個あっても一つの式で表すことができるようになりました。便利ですね。
5.2 重回帰分析
\(y\)を予測するという意味では，もちろん変数は多い方が良いでしょう。「身長」を予測するうえで，体重だけでなく「性別」や「体脂肪率」といったことがわかれば，予測はより正確になるはずです。 回帰分析でも，説明変数を複数個用いることが出来ます。これを一般的には重回帰分析と呼びます。 説明変数が\(K\)個あるならば，対応する回帰係数を\(K+1\)（切片の分）個用意して，以下のような直線を考えるわけです2。 \[ y = b_0 + b_1x_1 + b_2x_2 +\cdots + b_kx_k+\cdots + b_Kx_K \tag{5.6}\]
ここでのポイントは，重回帰分析では変数の効果が線形和（重み付け和）になっているという点です。回帰係数は「その説明変数の値が1大きくなったら\(y\)の予測値がどれだけ大きくなるか」を示していますが，最もベーシックな重回帰分析モデルの場合
- 説明変数の値がいくつであってもその効果は一定
- 他の説明変数の値は完全に無関係
であることが仮定されています。もし高次の効果（e.g., 薬は適量ならば飲むほど健康に良いが，飲み過ぎるとかえって良くない＝二次の効果）や交互作用を考慮したい場合には，直接それを表す項を追加する必要があります。例えば \[ y = b_0 + x_1b_1 + x_2b_2 + x_1^2b_3 + x_1x_2b_4 \tag{5.7}\] といった感じです。
また，重回帰分析で得られる回帰係数は，厳密には偏回帰係数と呼ばれます。これは「他の説明変数の値が固定されているときに，その説明変数の値が1大きくなったら\(y\)の予測値がどれだけ大きくなるか」を表しています。 もう少し正確に言うと，その説明変数以外で\(y\)を予測した際の誤差に対して，その説明変数のみで単回帰分析をした際の回帰係数が偏回帰係数です。 例えば2変数\(x_1,x_2\)の重回帰における\(x_1\)の偏回帰係数\(b_1\)は， \[ \begin{alignedat}{2} y &= b_{01} + b_2x_2 + \varepsilon_1 & \quad (\mathrm{Step} 1) \\ \varepsilon_1 &= b_{02} + b_1x_1 + \varepsilon_2 & \quad (\mathrm{Step} 2) \end{alignedat} \tag{5.8}\] という二段階で推定することで，単回帰の組み合わせに分解することができるのです（Step 1の左辺は\(\hat{y}\)ではなく\(y\)である点に注意）。 これにより，偏回帰係数は他の変数の影響を完全に取り除いた（コントロールした）上でのある変数の影響の大きさを表している，と解釈できるわけです。
5.2.1 重回帰分析の線形代数的表現
説明変数の数が増えても，同様に線形代数による表現を利用します。 (5.6)式に基づく予測を，まず\(p\)番目のデータ一つについて考えてみます。 説明変数が何個になっても，観測値\(y_p\)を予測値\(\widehat{y_p}\)と誤差\(\varepsilon_p\)に分ける点(5.2式)は変わりません。 \[
\begin{aligned}
\begin{split}
y_p &= \widehat{y_p} + \varepsilon_p \\
&= b_0 + b_1x_{p1} + b_2x_{p2} +\cdots + b_Kx_{pK}+ \varepsilon_{p}
\end{split}
\end{aligned}
\tag{5.9}\] これ以降，説明変数には2つの添字が付きます。 2つ目の添字\(k (k=1,2,\cdots,K)\)は，何番目の説明変数であるかを表すものです。 例えば\(x_{p3}\)（または\(x_{p,3}\)）は「\(p\)番目の人の\(3\)番目の説明変数の値」（dat[p,3]）を指しています。 添字の順序は，Rでデータフレームの行と列の要素を指定するときの順番（apply()関数の引数MARGINの指定）だと覚えると良いかもしれません（個人の感想）。
まずは(5.9)式の\(b_1x_{p1} + b_2x_{p2} +\cdots + b_Kx_{pK}\)（切片と誤差項以外）の部分について，ベクトルの積を使って簡略化していきます。 これは\(p\)番目のデータにおける説明変数ベクトル\(\symbf{x}_p=[x_{p1}, x_{p2}, \cdots, x_{pK}]\)と，回帰係数ベクトル\(\symbf{b}=[b_1, b_2, \cdots, b_K]^\top\)を使うと， \[ \begin{aligned} \begin{split} \symbf{x}_p\symbf{b} &= \begin{bmatrix} x_{p1} & x_{p2} & \cdots & x_{pK} \end{bmatrix}\begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_K \end{bmatrix} \\ &= x_{p1}b_1 + x_{p2}b_2 +\cdots + x_{pK}b_K \end{split} \end{aligned} \tag{5.10}\] と，かなりシンプルに表すことが出来ました。 ここでもう少し工夫してみます。 せっかくなので，切片についても同じようにまとめてしまいましょう。 (5.9)式の\(b_0\)の部分は，\(b_0\times 1\)と見ることも可能です。 \(b_1\)には\(x_{p1}\)がかかっていたのと同じように考えるならば，\(b_0\)の部分は\(x_{p0}=1\)ということです。 このように考えて，説明変数ベクトルと回帰係数ベクトルをそれぞれ\(\symbf{x}_p=[1, x_{p1}, x_{p2}, \cdots, x_{pK}]\)，\(\symbf{b}=[b_0, b_1, b_2, \cdots, b_K]^\top\)と書き換えてやれば， \[ \begin{aligned} \begin{split} \symbf{x}_p\symbf{b} &= \begin{bmatrix} 1 & x_{p1} & x_{p2} & \cdots & x_{pK} \end{bmatrix}\begin{bmatrix} b_0 \\ b_1 \\ b_2 \\ \vdots \\ b_K \end{bmatrix} \\ &= b_0 + x_{p1}b_1 + x_{p2}b_2 +\cdots + x_{pK}b_K \\ &= \widehat{y_p} \end{split} \end{aligned} \tag{5.11}\] というように，切片項まで含めて回帰直線による予測値\(\widehat{y_p}\)を簡略化できました。
あとはこれを\(P\)個のデータ全体に拡張するだけです。 といっても考え方は簡単で，\(P\times (K+1)\)の説明変数全体（\(+\)切片）を \[ \begin{aligned} \symbf{X} = \begin{bmatrix} \symbf{x}_1 \\ \symbf{x}_2 \\ \vdots \\ \symbf{x}_P \end{bmatrix} = \begin{bmatrix} 1 & x_{11} & x_{12} & \cdots & x_{1K} \\ 1 & x_{21} & x_{22} & \cdots & x_{2K} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{P1} & x_{P2} & \cdots & x_{PK} \end{bmatrix} \end{aligned} \tag{5.12}\] と表せば，これを用いてすべてのデータに関する予測値\(\hat{\symbf{y}}\)を \[ \begin{aligned} \hat{\symbf{y}} = \begin{bmatrix} \hat{y}_1 \\ \hat{y}_2 \\ \vdots \\ \widehat{y_p} \end{bmatrix} &= \symbf{X}\symbf{b} \\ &= \begin{bmatrix} 1 & x_{11} & x_{12} & \cdots & x_{1K} \\ 1 & x_{21} & x_{22} & \cdots & x_{2K} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{P1} & x_{P2} & \cdots & x_{PK} \end{bmatrix}\begin{bmatrix} b_0 \\ b_1 \\ b_2 \\ \vdots \\ b_K \end{bmatrix} \\ &= \begin{bmatrix} b_0 + x_{11}b_1 + x_{12}b_2 +\cdots + x_{1K}b_K \\ b_0 + x_{21}b_1 + x_{22}b_2 +\cdots + x_{2K}b_K \\ \vdots \\ b_0 + x_{P1}b_1 + x_{P2}b_2 +\cdots + x_{PK}b_K \end{bmatrix} \end{aligned} \tag{5.13}\] とまとめることが可能です。あとは誤差ベクトルを付け加えたら，以下のようにスッキリとした表現の出来上がりです。
因子分析やSEMのところでは，このような感じで「変数の行列」\(\times\)「係数のベクトル（または行列）」の積を用いて手法のコンセプトを紹介していきます。 ということで，今のところはここで紹介した記法に慣れておいてください。
正規方程式
上記のように重回帰分析を線形代数で表現すると，最小二乗法の解も解析的に求めることが出来ます。 いま，求めたいのは\(\symbf{\varepsilon}^\top\symbf{\varepsilon}\)が最小になるような\(\symbf{b}\)の値でした。 そこで，\(\symbf{\varepsilon}\)を\((\symbf{y} - \symbf{X}\symbf{b})\)に戻して考えると，\(\symbf{\varepsilon}^\top\symbf{\varepsilon}=(\symbf{y} - \symbf{X}\symbf{b})^\top(\symbf{y} - \symbf{X}\symbf{b})\)が最小になるような\(\symbf{b}\)を求めたら良いわけです。
最小値になる\(\symbf{b}\)を求めたいわけなので，ちょっと大変かもしれませんが，行列を展開して\(\symbf{b}\)で偏微分したものイコール0という式をとれば3， \[ \symbf{X}^\top\symbf{X}\symbf{b} = \symbf{X}^\top\symbf{y} \] というかたちになります。この方程式のことを正規方程式と呼びます。 あとは\(\symbf{X}^\top\symbf{X}\)が正則であれば，両辺に逆行列をかけることで，この式を\(\symbf{b}=\)の形に変形させ， \[ \symbf{b} =(\symbf{X}^\top\symbf{X})^{-1} \symbf{X}^\top\symbf{y} \] という解が得られます。
ちなみに「\(\symbf{X}^\top\symbf{X}\)が正則でない」ときには逆行列が求められないため，解を得ることが出来ません。 このような状態になるのは，行列がランク落ちしている場合ですが，ランク落ちが発生するのは\(\symbf{X}\)の特定の変数が線形従属になっている場合，つまり他の変数の線形和で表せてしまう場合です。 回帰分析ではよく「多重共線性に気をつけましょう」という話がありますが，この理由として，完全な多重共線性がある場合には\(\symbf{X}^\top\symbf{X}\)が正則でなくなってしまうために，解が求められなくなってしまうから，という説明も可能なのです。
5.2.2 （おまけ）ダミー変数
回帰係数は「その説明変数の値が1大きくなったら\(y\)の予測値がどれだけ大きくなるか」を示しています。では，説明変数が名義変数の場合はどうしたら良いでしょうか。 まずはカテゴリ数が2の場合（e.g., 生物学的な性：男女）を考えてみます。通常，このようなデータでは一方のカテゴリに1を，もう一方のカテゴリに0をあてます。今回は「男性は0，女性は1」としておきましょう。この「性別\((x_{p2})\)」と「体重\((x_{p1})\)」から「身長\((y_p)\)」を予測する重回帰モデルを立てると \[ \widehat{y_p} = x_{p1}b_1 + x_{p2}b_2 + b_0 \tag{5.14}\] となります。このモデルを男性と女性それぞれに分けてみてみると，男性は\(x_2=0\)，女性は\(x_2=1\)なので \[ \begin{alignedat}{3} \widehat{y_p} &= x_{p1}b_1 & & + b_0 & \quad & \text{(男性)} \\ \widehat{y_p} &= x_{p1}b_1 + b_2 & & + b_0 & & \text{(女性)} \end{alignedat} \tag{5.15}\] となります。したがって，男性モデルでは切片が\(b_0\)となっており，女性モデルでは切片が\(b_2+b_0\)となっているわけです。回帰係数の解釈通り，\(b_2\)は\(x_2\)の値が1大きくなった際に\(y\)の予測値がどれだけ大きくなるかを意味するわけですが，より正確に言えば体重\(x_{1p}\)の値が同じ男性と女性がいた場合，身長は平均的にどれだけ異なるかを表しているわけですね。
カテゴリ数が3の場合はこうはいきません。先程の例について，性別の代わりに血液型を\(x_2\)としてみます。血液型はA, B, O, ABをそれぞれ1, 2, 3, 4とコーディングしたものだとすると，重回帰モデルは \[ \hat{y}_i = \left\{\begin{alignedat}{3} x_{p1}b_1 &+ &b_2 &+ b_0 & \quad (A) \\ x_{p1}b_1 &+ 2&b_2 &+ b_0 & \quad (B) \\ x_{p1}b_1 &+ 3&b_2 &+ b_0 & \quad (O) \\ x_{p1}b_1 &+ 4&b_2 &+ b_0 & \quad (AB) \end{alignedat}\right. \tag{5.16}\] となります。つまりA型-B型の差とB型-O型の差とO型-AB型の差がすべて同じと，明らかにおかしなことになっています。このように，名義変数についてそのまま対応可能なカテゴリ数は2までなので，カテゴリ数が3以上の場合には，そのまま数値化して投入するのではなく，二値のダミー変数化することで対応します。
血液型の場合，4カテゴリなので3つのダミー変数\((x_{2A}, x_{2B}, x_{2O})\)および対応する回帰係数\((b_{2A}, b_{2B}, b_{2O})\)を用意します。これらのダミー変数はそれぞれ
- \(x_{2A}\)はA型の場合1，それ以外の場合0になる
- \(x_{2B}\)はB型の場合1，それ以外の場合0になる
- \(x_{2O}\)はO型の場合1，それ以外の場合0になる
と設定し，4つの血液型に対してダミー変数はそれぞれ以下のような値を取ります。
| 血液型 | \(x_{2A}\) | \(x_{2B}\) | \(x_{2O}\) |
|---|---|---|---|
| A型 | 1 | 0 | 0 |
| B型 | 0 | 1 | 0 |
| O型 | 0 | 0 | 1 |
| AB型 | 0 | 0 | 0 |
こうすることで重回帰モデルは \[ \hat{y} = \left\{\begin{alignedat}{3} x_{p1}b_1& + b_{2A} &+ b_0 & \quad (A) \\ x_{p1}b_1& + b_{2B} &+ b_0 & \quad (B) \\ x_{p1}b_1& + b_{2O} &+ b_0 & \quad (O) \\ x_{p1}b_1&& + b_0 & \quad (AB) \end{alignedat}\right. \tag{5.17}\] と書くことができ，各回帰係数はAB型との差として解釈可能になります。 ここでのポイントは，ダミー変数はカテゴリ数\(-1\)個だという点です。なぜカテゴリ数ぶんのダミー変数があると困るのか考えてみましょう。例えば上の3つのダミー変数に加えて「AB型なら1」となる\(x_{2AB}\)および回帰係数\(b_{2AB}\)があるとします。最小二乗法で推定した結果，\((b_{2A}, b_{2B}, b_{2O},b_{2AB})\)がそれぞれ\((1,2,3,4)\)，また切片\(b_0\)が\(0\)だったとしましょう。これを重回帰モデルで表すと \[ \hat{y} = \left\{\begin{alignedat}{3} x_{p1}b_1& + 1 &+ 0 & \quad (A) \\ x_{p1}b_1& + 2 &+ 0 & \quad (B) \\ x_{p1}b_1& + 3 &+ 0 & \quad (O) \\ x_{p1}b_1& + 4 & + 0 & \quad (AB) \end{alignedat}\right. \tag{5.18}\] となります。ですが，この式には別の解が考えられます。例えば\((b_{2A}, b_{2B}, b_{2O},b_{2AB})\)がそれぞれ\((-4,-3,2,1)\)，切片\(b_0\)が\(5\)だとしても，重回帰式は \[ \hat{y} = \left\{\begin{alignedat}{3} x_{1p}b_1& -4 &+ 5 & \quad (A) \\ x_{1p}b_1& -3 &+ 5 & \quad (B) \\ x_{1p}b_1& -2 &+ 5 & \quad (O) \\ x_{1p}b_1& -1 & + 5 & \quad (AB) \end{alignedat}\right. \tag{5.19}\] となり，結果的に(5.18)式と全く同じになってしまいました。 このように，回帰分析ではダミー変数がカテゴリ数の数だけあると解が一意に定まらなくなってしまうため，カテゴリ数-1個だけ用意する必要があるのです4。
ダミー変数がカテゴリ数より少ないとなると，必然的にダミー変数が与えられない（全てのダミー変数が0であることによって表される）カテゴリが発生します。このカテゴリのことを基準カテゴリや参照カテゴリと呼んだりしますが，この基準カテゴリの決め方も重要になります。というのも回帰係数は基準カテゴリとの差であるためです。回帰分析では，回帰係数の検定（\(H_0: b=0\)）が行われるため，「あるカテゴリが基準カテゴリと平均的に差があるか」は検証できる一方で，基準カテゴリ以外のカテゴリ同士での差の検定はそのままでは出来ません。実験的な環境であれば対照群を基準カテゴリにおくのが良いでしょう。
5.2.3 Rで重回帰分析
↓本Chapterで使用するファイルのダウンロードはこちらから
ここらで少し，Rでの重回帰分析のやり方を紹介しておきましょう。Rでは，lm()という関数があります（linear modelの略）。今回は試しに「年齢age」と「性別gender」の2つを説明変数として，第1因子の5項目の合計点（Q1_A）を結果変数とします。
lm()を始めとするRのいくつかの関数では，説明変数と結果変数の関係を表すために，以前少しだけ登場した特殊な記法（formula）を使用します。
第一引数には回帰モデルの式(formula)を与えます。上の例ではQ1_A ~ age + genderが第一引数です。見方としては重回帰モデル式\(y = x_1b_1 + x_2b_2\)と同じですが，両辺をチルダ(~)でつなぐのが特徴です。とりあえずこの授業の中ではチルダで結んだら回帰ということを覚えておきましょう。実はSEM （ チャプター 7 ） で使用するlavaanパッケージの記法でもチルダは回帰を表します。
formulaで使える記号
基本的には重回帰分析のように+で説明変数を足していけば良いのですが，他にもいくつかの記号があります。
- 2つの説明変数を
:でつなぐと，その変数間の交互作用項を指定できます。例えばx1とx2があるときに，y ~ x1:x2とすると，これは\(y = x_1x_2b_{12} + b_0\)という回帰式を表します。 - 2つの説明変数を
*でつなぐと，その変数の主効果と交互作用項を同時に指定できます。例えばy ~ x1*x2とすると，これは\(y = x_1b_1 + x_2b_2 + x_1x_2b_{12} + b_0\)という回帰式を表します。 - 0を足すと，切片項\(b_0\)が0に固定されます。原点を通る回帰をしたい場合に使えるかもしれません。例えば
y ~ x1+x2+0とすると，これは\(y = x_1b_1 + x_2b_2\)という回帰式を表します。 - 変数の和や積などを説明変数として使いたい場合は，
I()をかませることができます。例えばy ~ I(x1+x2)とすると，これは\(y = (x_1+x_2)b_{12} + b_0\)という回帰式を表します。ただこれを使うくらいなら，事前にデータフレームに新しい変数を作成しておいたほうがスマートな気がします。
それでは出力を見てみましょう。
下に出ているCoefficientsが（回帰）係数を指しています。(Intercept)が切片を，それ以外のものは各説明変数に対する回帰係数を表しています。したがって，重回帰モデルの式は \[
\widehat{y_p} = 18.05453 + 0.07083x_{p,\mathrm{age}}+ 1.89117x_{p,\mathrm{gender}}
\] となります。変数genderは二値変数のため，男性（gender==1）と女性(gender==2)で分けると， \[
\widehat{y_p} = \left\{\begin{alignedat}{3}
18.05453 + 0.07083x_{p,\mathrm{age}}+ 1.89117 & \quad \text{(男性)} \\
18.05453 + 0.07083x_{p,\mathrm{age}}+ 3.78234 & \quad \text{(女性)}
\end{alignedat}\right.
\] ということですね。二値カテゴリ変数のコーディングに関して，通常は0と1にするのですが，これは0のカテゴリを基準カテゴリと見なすためです。ただ回帰係数という観点で言えば，0と1にしないといけないということはなく，差が1ならば何でも良い5ことになります。 もしdatでのgenderの値が全員1ずつ小さい値で（つまり男性は0，女性は1と）コーディングされていたとしても，genderに対する回帰係数は変わりません。少し切片が変わって \[
\begin{alignedat}{2}
\widehat{y_p} &= (18.05453+1.89117) & &+ 0.07083x_{p,\mathrm{age}}+ 1.89117x_{p,\mathrm{gender}} \\
&= 19.9457 & &+ 0.07083x_{p,\mathrm{age}}+ 1.89117x_{p,\mathrm{gender}} \\
\end{alignedat}
\] となります。男女ごとに回帰式を見ると \[
\widehat{y_p} = \left\{\begin{alignedat}{3}
19.9457 &+{} &0.07083x_{p,\mathrm{age}}& & \quad \text{(男性)} \\
19.9457 &+{} & 0.07083x_{p,\mathrm{age}}&+ 1.89117 & \quad \text{(女性)}
\end{alignedat}\right.
\] となるわけです。
切片の役割
切片は「すべての説明変数の値が0のときの予測値」を表しています。したがってdatで言えば「ageが0＝0歳で，genderが0の人」の予測値になりますが当然そんな人はいません。 このように，多くの場合では切片の値それ自体は使えない（検定する意味もない）ものです。
もし切片に役割を持たせたい場合には，すべての量的変数を中心化すると良いです。中心化，つまり平均値を引くことで各変数の値が0というのが「その変数が平均値の人」を表すようになります。 つまり全ての量的変数を中心化した状態で行った回帰分析の切片は「すべての変数が平均値の人」の予測値になるわけです。
なお，genderのようなカテゴリカル変数は中心化してもしなくても良いです。例えば男女比が1:1のときに中心化を行うと「男性は-0.5，女性は0.5」という感じになります。こうなるとむしろ0が意味を持たなくなってしまうので，あえて中心化しないことで，切片項は「量的変数はすべて平均値の男性での平均値」を意味するようになります。 一方で，カテゴリカル変数も全て中心化した場合，切片項は純粋に全体平均値を表すようになります。ということでどちらにせよ解釈可能な意味を持つので，用途に応じて中心化するかを決めるのが良いでしょう。
とりあえず回帰分析ができたので，次は回帰係数の検定をしてみます。といってもlm()には既に回帰係数の検定が用意されているので難しいことはありません。
Rでは，関数の出力を含むあらゆるものをオブジェクト（変数）に代入することが出来ます。これにより，例えば「因子分析を行い，結果から因子負荷行列を取り出し，その行ごとの和をとる」みたいなことが全てコードとして書けるようになるわけです。 同様に，特定の関数の出力を受け取って別の処理を行うような関数もたくさん存在しています。ここでは関数の出力自体も変数として扱えるという感覚を理解しましょう。
何かしらの分析を行う関数の出力オブジェクトは，たいていlist型で与えられます。list型はほぼ何でも，いくつ入れても良い型です。例えばlist型であるresult_lm（lm()の出力）の中身を見てみると，以下のような状態になっています。
List of 12
$ coefficients : Named num [1:3] 18.0545 0.0708 1.8912
..- attr(*, "names")= chr [1:3] "(Intercept)" "age" "gender"
$ residuals : Named num [1:2432] -1.079 -2.112 -4.041 -0.041 -1.15 ...
..- attr(*, "names")= chr [1:2432] "1" "2" "3" "4" ...
$ effects : Named num [1:2432] -1.15e+03 4.00e+01 -4.38e+01 8.35e-02 -1.19 ...
..- attr(*, "names")= chr [1:2432] "(Intercept)" "age" "gender" "" ...
$ rank : int 3
$ fitted.values: Named num [1:2432] 21.1 23.1 23 23 21.1 ...
..- attr(*, "names")= chr [1:2432] "1" "2" "3" "4" ...
$ assign : int [1:3] 0 1 2
$ qr :List of 5
..$ qr : num [1:2432, 1:3] -49.3153 0.0203 0.0203 0.0203 0.0203 ...
.. ..- attr(*, "dimnames")=List of 2
.. .. ..$ : chr [1:2432] "1" "2" "3" "4" ...
.. .. ..$ : chr [1:3] "(Intercept)" "age" "gender"
.. ..- attr(*, "assign")= int [1:3] 0 1 2
..$ qraux: num [1:3] 1.02 1.02 1.02
..$ pivot: int [1:3] 1 2 3
..$ tol : num 1e-07
..$ rank : int 3
..- attr(*, "class")= chr "qr"
[list output truncated]
- attr(*, "class")= chr "lm"一番上にList of 12とあることから，このオブジェクトはいろいろなものが12個くっついている，ということがわかります。 上の出力では，$記号で区切られた一つ一つがlist内の各要素です。 つまり一つ目がcoefficientsで，これは長さ3の名前付き実数型(Named num)のベクトルとなっています。その下のresidualsやeffectは同じく名前付き実数型ベクトルですが長さは2432のようです。また，少し下にあるqrはList of 5となっており，字下げされた5つの要素(qr, qraux, pivot, tol, rank)が存在しています。これは，listの中にlistが入れ子になっている，という状態を表しています。 このように，list型オブジェクトは型の違いも気にせずにいろいろなものをくっつけて一つのオブジェクトとして扱うことが出来ます。
list型オブジェクトの中身は，それぞれの要素名の前に$がついていることから分かるように$記号を使って取り出すことが出来ます6。 例えば以下のコードでは，result_lmの中から回帰係数の部分(coefficients)だけをベクトルとして取り出すことができます。この行為に意味があるかはともかく，大抵のオブジェクトでは分析結果から中身を取り出せるという感覚だけでも理解しておいてください。 コレ，分析の手順の自動化率を高める際などにかなり重要になってきます。
今回はlm()関数の出力をresult_lmというオブジェクトに代入しました。そしてこれに対してsummary()関数を実行しました。 Chapter 2ではsummary()関数のことを「要約統計量を出してくれる関数」と紹介しましたが，実際にはsummary()関数はもっと広く「与えられたオブジェクトの型に合わせた何かしらのサマリーを出してくれる」という関数なのです7。
Call:
lm(formula = Q1_A ~ age + gender, data = dat)
Residuals:
Min 1Q Median 3Q Max
-19.1742 -2.6150 0.6091 3.1820 8.8502
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 18.054531 0.394846 45.726 <2e-16 ***
age 0.070829 0.008116 8.727 <2e-16 ***
gender 1.891169 0.189308 9.990 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 4.386 on 2429 degrees of freedom
Multiple R-squared: 0.07011, Adjusted R-squared: 0.06934
F-statistic: 91.56 on 2 and 2429 DF, p-value: < 2.2e-16出力は上から，
Residuals- \(y-\hat{y}\)の要約統計量です。回帰分析の前提条件として，誤差\(\varepsilon\)は正規分布\(N(0,\sigma_{\varepsilon}^2)\)に従う必要があるため，特に中央値が0から大きく離れていたら注意が必要かもしれません。
Coefficients- 回帰係数です。左から「係数の推定値」「標準誤差」「\(t\)統計量」「\(p\)値」が表示されています。今回の場合，いずれも\(p<.05\)なので，統計的に有意ということですね。
Multiple R-squared- 重相関係数です。この後説明します。
Adjusted R-squared- 自由度調整済み重相関係数です。この後説明します。
F-statistic- 「切片以外の回帰係数が全て0である」という帰無仮説に対する\(F\)統計量です。ということはこの検定が有意ではなかった場合，モデルとしての意味が無いことになります。
5.2.4 決定係数・重相関係数
summary(lm())で出てくるMultiple R-squaredは決定係数と呼ばれます。回帰分析モデルでは，結果変数\(y\)は予測値\(\hat{y}\)と誤差\(\varepsilon\)によって \[
y=\hat{y} + \varepsilon
\tag{5.20}\] と表されます。当然ながら，予測値と誤差の間は無関係であるはずなので8，\(y\)の分散は \[
\sigma^2_y = \sigma^2_{\hat{y}} + \sigma^2_{\varepsilon}
\tag{5.21}\] というように，予測値と測定誤差の分散の単純な和として表すことができます。信頼性係数のときと同じ感じですね。 このとき，決定係数\(R^2\)は \[
R^2=\frac{\sigma^2_{\hat{y}}}{\sigma^2_y}=1-\frac{\sigma^2_{\varepsilon}}{\sigma^2_y}
\tag{5.22}\] と定義されます。つまり，決定係数\(R^2\)は結果変数の分散のうち，説明変数で説明可能な分散の割合ということです。
ここで，\(y\)に影響（個人差）を与えるすべての説明変数が分かっている状況を考えてみましょう。例えばQ1_Aの値を決定づけるものは，幼いときの親の関わり方や小学校での友人関係，あるいは昨日の晩御飯や体温，回答の瞬間の気分なんかも影響するかもしれません。ほぼゼロだとしてもゼロではない限りは重回帰モデルに含める意味があります。仮にちょうど1億個の説明変数を使えば\(y\)の個人差が完全に説明可能だったとすると，重回帰モデルは，以下のようになります（左辺が\(\hat{y}\)ではなく\(y\)である点に注意）。 \[
y_p=b_0 + x_{p,1}b^{*}_1 + x_{p,2}b^{*}_2 + x_{p,3}b^{*}_3 + \cdots + x_{p,99999999}b^{*}_{99999999}+ x_{p,100000000}b^{*}_{100000000}
\tag{5.23}\] ただ，実際問題として1億個の説明変数による回帰モデルが判明したとしても，このままでは変数の数が多すぎて実社会には応用できません。1億個あっても，大半はほぼ無視できるレベルの影響しか与えていないでしょうし，できることならなるべく少ない変数の数で十分な予測モデルを立てることができれば，みんな嬉しいはずです（オッカムの剃刀）。 そこで，この1億個の変数の中から，最も説明力が高い2つだけを選んできたとしましょう。今，1億個の説明変数が「説明力の高い順」に並んでいたとすると，上の重回帰モデルは次のように書き換えることができます。 \[
\begin{aligned}
y&=\hat{y} + \varepsilon \\
\hat{y} &= b_0 + x_1b_1 + x_2b_2 \\
\varepsilon &= x_3b_3 + \cdots + x_{99999998}b_{99999998}+ x_{99999999}b_{99999999}+ x_{100000000}b_{100000000}
\end{aligned}
\tag{5.24}\] もちろん，(5.24)式の場合には，観測された\(y\)を完全には説明できません。しかし，もしも説明変数2つで\(y\)の個人差のうちの結構な割合が説明できるとしたら，実社会への応用はかなり現実味を帯びてきます。 そもそも人間の行動を完全に予測するなんてのは無理な話なので，「効率よく大体予測できたら良い」くらいの気持ちで考えておけばよいわけです。 このように，回帰分析では，どれだけ少ない変数で十分な説明ができるかが一つの重要な指標となります。
また，Multiple R-squaredはその名の通り重相関係数の二乗という意味合いもあります。重相関係数とは，\(\symbf{y}\)と\(\hat{\symbf{y}}\)の相関のことです。実際に相関係数を出してみましょう。なおpredict()関数は，lm()の出力を第一引数に，データを第二引数に与えると，各行の説明変数の値とlm()で得られた回帰係数を用いて\(\hat{\symbf{y}}\)を計算してくれる関数です。
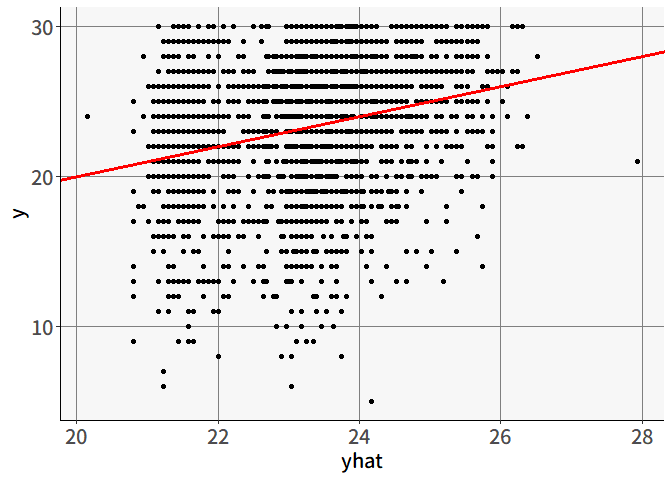
確かにsummary(lm())で出てくるMultiple R-squaredと一致する値が得られました。 重相関係数が大きいほど，説明変数による予測\(\hat{y}\)は正確であるということです。ちなみに重相関係数が1になるのは，\(y=\hat{y}\)のときのみです。今回の例では，\(R^2=0.0701\)とかなり低い値を示しました。実際に散布図を見ても， 図 5.7 のように予測はほとんど意味をなしていません。 これは，Q1_Aの得点の変動を説明するのに年齢ageと性別genderは少なくとも線形ではほぼ意味をなさない（説明できてない）ということです。このように，重相関係数はモデルの適合度の指標としても用いることができます。 具体的にどの程度あれば十分という基準は特にないのですが，あまりに低い場合には，回帰係数の検定が有意であったとしても「でも，結局誤差のほうが大きいんだよね？」という感じで評価されてしまうかもしれません。
回帰分析では，説明変数の数を増やすと必ず重相関係数は高くなります。仮に完全に無関係な変数（乱数など）を加えたとしても，重相関係数が低下することはありません。 先程の1億個モデルで言えば，最も意味のない変数\(x_{100000000}\)を追加したとしても， \[ \begin{aligned} y&=\hat{y} + \varepsilon \\ \hat{y} &= x_1b_1 + x_2b_2 + x_{100000000}b_{100000000} + b_0 \\ \varepsilon &= x_3b_3 + \cdots + x_{99999998}b_{99999998}+ x_{99999999}b_{99999999} \end{aligned} \] となるわけで，わずかでも\(\sigma^2_{\varepsilon}\)は小さくなるでしょう。
どれだけ少ない変数で十分な説明ができるかという視点では，重相関係数がほぼ向上しない無駄な変数は取り除きたいところです。 そこで使われることがあるのが自由度調整済み決定係数です。これは，決定係数\(R^2\)に対して説明変数の数によるペナルティを与えたものです。つまり決定係数が同じになるならば，説明変数の数が少ないモデルのほうが良い値を示します。
\[ R^2_{adj}=1-\frac{\sigma^2_{\varepsilon}}{\sigma^2_y}\frac{n-1}{n-k-1} \] 一部の人はこの\(R^2_{adj}\)を，説明変数の数が異なるモデル同士の比較（ある変数を入れるか入れないかの判断など）に用いているようです。ただ，式を見てわかるように\(R^2_{adj}\)にかかるペナルティはサンプルサイズ\(n\)の影響も受けています。つまり，サンプルサイズが大きくなるほど説明変数の追加に対するペナルティが弱くなるため，ほぼ無意味な変数を加えることによる\(\sigma^2_{\varepsilon}\)の減少のほうがペナルティよりも大きくなる可能性が高まります。そして結果的に変数の数が多いモデルのほうが選ばれやすくなる，という問題点があったりします。
…ということで長々と決定係数・重相関係数についてお話をしましたが，基本的には自由度調整済み決定係数\(R^2_{adj}\)はあまり使えるものではない，という認識でも良いような気がします9。
5.2.5 標準偏回帰係数
偏回帰係数は，それぞれ「その説明変数が1大きくなったら\(\hat{y}\)はどの程度大きくなるか」を表しているため，そのままでは比較することができません。ageとgenderの係数を比べてgenderのほうが影響が大きい，と判断はできないのです。 その理由の一つは，変数のスケールが異なるためです。ageが1増えると言うのは，年齢が一つ変わるだけでさほど大きな変化ではありません。対してgenderが1増えると言うのは，性別が男性から女性に変わることを意味するため，これはかなり大きな変化です。 変数の変化の程度を調整するための方法として標準化というものがありました。標準化したあとの変数は，すべて平均0，分散1になるため，どんな変数でも「1増える」ということの意味が「1標準偏差増える」に揃えられます。
標準偏回帰係数とは，説明変数と結果変数のすべてを標準化した上で算出された偏回帰係数のことです。結果変数も標準化することによって，係数は「説明変数が1標準偏差大きくなったら，\(y\)が標準偏差いくつ分大きくなるか」を表すことになり，異なる変数の間でも大小の比較が可能そうな気がしてきます。
Rには標準化を行う関数としてscale()というものがあります。
ということで，これを使って標準偏回帰係数を出してみましょう。
Call:
lm(formula = Q1_A ~ age + gender, data = dat_std)
Residuals:
Min 1Q Median 3Q Max
-4.2178 -0.5752 0.1340 0.7000 1.9468
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.364e-16 1.956e-02 0.000 1
age 1.709e-01 1.958e-02 8.727 <2e-16 ***
gender 1.956e-01 1.958e-02 9.990 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.9647 on 2429 degrees of freedom
Multiple R-squared: 0.07011, Adjusted R-squared: 0.06934
F-statistic: 91.56 on 2 and 2429 DF, p-value: < 2.2e-16ageの係数が1.709e-01，つまり\(1.709\times10^{-1}=0.1709\)，そしてgenderの係数が1.956e-01，つまり\(1.956\times10^{-1}=0.1956\)となりました。この標準偏回帰係数を比較することで，やはりgenderのほうがQ1_Aに与える影響は大きそうだ，ただあまり差はなさそうだ，ということがわかりました。
標準偏回帰係数による変数の比較は，常に良い方法ではないとされています。 標準化という手続きは，単純に平均値を引いてから標準偏差で割るだけです。したがって標準化前後では変数の分布は変わりません。ageとgenderを見ても，genderは二値変数のため，分布の形はageとは完全に別物でしょう。そのような状況下で，2つの変数の「1標準偏差」の意味は同じなのでしょうか。 King （1986） では，比較する変数の間に共通の単位があるような場合には標準化は有効だが，そうでなければ比べようがないとしています。安易に標準偏回帰係数を使うのは危険かもしれない，ということです。
5.3 一般化線形モデル
ここまで説明してきた回帰分析モデルは，
- 説明変数の単純な線形結合で結果変数を予測し
- 誤差は全データで共通の正規分布\(N(0,\sigma_{\varepsilon}^2)\)に従う
という仮定のもとでのモデルでした。ただ，世の中にはそんなに単純ではないケースが結構あります。例えば結果変数が「病気になるかどうか」の場合，取りうる値は0（病気にならない）か1（病気になる）の2つのみです。 ですがこれまでの回帰モデルでは説明変数が増える（減る）ごとに\(\hat{y}\)は際限なく大きく（小さく）なってしまうため，直線を当てはめるのはちょっと嫌な感じです。
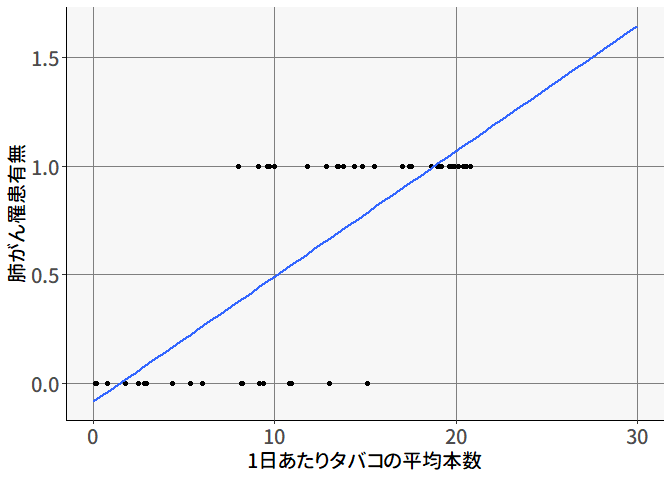
この関係を表したものが 図 5.8 です。X軸には説明変数として「1日あたりタバコの平均本数」を，Y軸には結果変数として「肺がんになったかどうか」をプロットしています。 普通に考えると，タバコの本数が多いほど肺がんになりやすいので，回帰直線を引くと右上がりになります。 ですが直線を引いてしまうと，20本を超えてもなお値は大きくなってしまいます。 実際に結果変数の取りうる値が0か1であるため，ここではY軸を「肺がんになる確率」として回帰直線を用いた予測をしようとすると，例えば1日にタバコを30本吸う人は肺がんになる確率が160%くらいになってしまいます。これは困りました…
また「誤差は正規分布\(N(0,\sigma_{\varepsilon}^2)\)に従う」という仮定に関しても問題がありそうです。 図 5.8 では，X軸が10本くらいのところでは罹患している人としていない人がばらばらといるため，それなりの分散がありそうな一方で，0本や20本のあたりでは全員が同じ値になっています。つまりX軸の値によって誤差分布の分散\(\sigma_{\varepsilon}^2\)が変動しているように思われるため，やはり直線を当てはめるのはおかしそうです。
ということで，回帰分析モデルを拡張する必要があります。予測値の変動を説明変数の線形結合で表した(5.6)式の右辺はわかりやすいのでこのまま使うとして，直線ではなく確率を表す，つまり取りうる値が0から1に収まるように変換することを考えます。 いくつか選択肢はあるのですが，ここではロジスティック変換をしてみましょう。 ロジスティック関数とは， \[ g(x) = \frac{1}{1+\exp(x)} \tag{5.25}\]
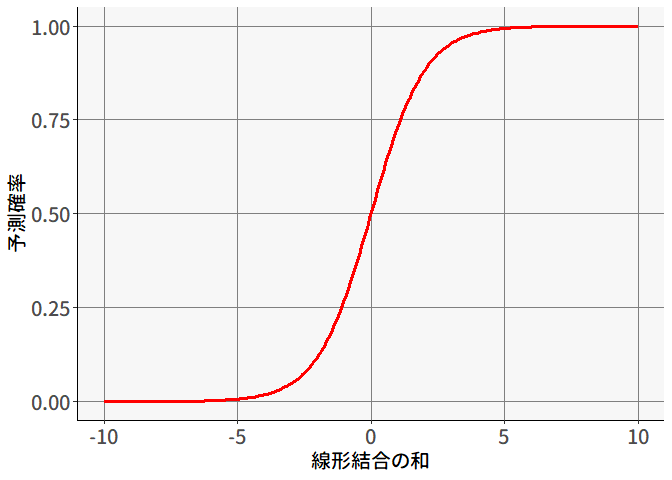
という関数です。 図 5.9 は，\(x\)の値が\(-10\)から\(10\)まで動いたときの\(g(x)\)の値を表したものです。 このように，ロジスティック関数は\(x\)の値が何であろうと確かに\(g(x)\)は0から1までに収まるようです。
ということで，ロジスティック関数の\(x\)を説明変数の線形和\(b_0 + x_1b_1 + x_2b_2 + x_3b_3 + \cdots + x_Kb_K\)に置き換えてあげれば， \[ y = \frac{1}{1+\exp\left[-(b_0 + x_1b_1 + x_2b_2 + x_3b_3 + \cdots + x_Kb_K)\right]} \tag{5.26}\]
となり，この右辺\(y\)は0から1までの値しか取らなくなります。 また，式を変形させると \[ \log\frac{y}{1-y} = b_0 + x_1b_1 + x_2b_2 + x_3b_3 + \cdots + x_Kb_K \tag{5.27}\] という形になり，もとのきれいな右辺に戻すことも可能です。
またこの変換では（誤差）分散の不均一性も表現しています。 というのは 図 5.9 を見るとわかるように，確率が0.5付近では説明変数の線形和（X座標）が少し変わるだけで予測確率が大きく変動するのに対して，確率が0または1付近の極端なエリアでは，ほとんど変動がなくなっています。
ということで，このように回帰分析モデルを変形させることで正規分布以外の分布にも対応可能にしたものが一般化線形モデル (generalized linear model; GLM)です10。 一般化線形モデルでは，モデル式が \[ g(y) = b_0 + x_1b_1 + x_2b_2 + x_3b_3 + \cdots + x_Kb_K \tag{5.28}\] という形になっています。つまり，「\(y\)をなんか変換したもの」である\(g(y)\)を\(x\)の線形和\(\symbf{Xb}\)で予測しようという試みなわけです。 この「\(y\)をなんか変換したもの」が，ロジスティック回帰の場合には \[ g(y) = \log\frac{y}{1-y} \] というロジット変換11の式になっており，またふつうの重回帰モデルも \[ g(y) = y \] という恒等関数によって変換されたものと見れば，これが一般化線形モデルの特殊なケースだということがわかるでしょう。 変換の関数\(g(y)\)はリンク関数と呼びます。リンク関数は「二項分布のときにはロジット変換」というように基本的には\(y\)の分布に対してお決まりのものがあります。 一般化線形モデルでは変形の形ごとに異なる名称がついており，ロジスティック変換を用いた場合をロジスティック回帰と呼びます。 もう少ししっかりとロジスティック回帰モデルの全体を書くと， \[ y_p = \frac{1}{1+\exp\left[-(b_0 + x_{p1}b_1 + x_{p2}b_2 + x_{p3}b_3 + \cdots + x_{pK}b_K)\right]} + \varepsilon_p, \quad \varepsilon_p \sim N(0,y_p(1-y_p)) \tag{5.29}\] となります。つまり誤差分散は確率が0.5付近では最も大きく，0や1付近では小さくなることを織り込んだ上でモデルのパラメタ（回帰係数）を推定しているのです。
プロビット回帰
リンク関数を標準正規分布累積確率関数の逆関数\(g(y)=\Phi^{-1}(y)\)と置いたGLMは，プロビット回帰と呼びます。 ロジスティック回帰とプロビット回帰はどちらも「結果変数が0か1の二値」というケースに対して適用されるモデルです。 そして2つの回帰で用いられるリンク関数の逆関数はよく似た形（左右対称の釣鐘型）をしています。 そんな2つの回帰モデルについて，特に経済学など？では理論的な背景なども考慮して厳密に使い分けられる節があるようなのですが，この講義で紹介する手法（特に項目反応理論）では，基本的にその区別には関心がありません。 言ってしまえば「どっちでも良い」という感じがあり，基本的には計算しやすいという理由からロジスティック回帰のほうを使用することが多いです。
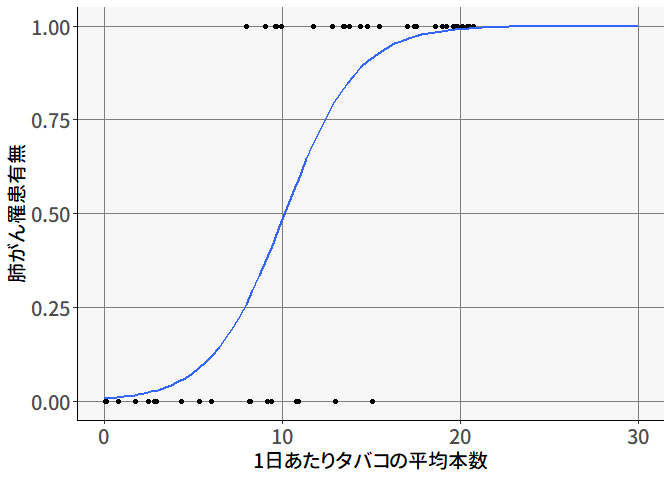
ということで，先程のタバコの例でもロジスティック回帰による回帰直線を当てはまると， 図 5.10 のようになります。
一般化線形モデルでは他にもポアソン回帰やガンマ回帰を始めとしていくつかありますが，ここでは全ては紹介しません。以降の回では，ロジスティック回帰だけ理解しておけばついていけるはずです。
5.3.1 Rで一般化線形モデル
Rで一般化線形モデルを行う場合は，lm()の代わりにglm()という関数を使います。基本的には使い方は同じですが，GLMなので「誤差分散の分布の形」および「リンク関数」を指定してあげる必要があります。指定の仕方にちょっとクセがありますが，そういうものとして理解してください。
Call:
glm(formula = Q1_A_binom ~ age + gender, family = binomial(link = "logit"),
data = dat)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.759336 0.189153 -9.301 < 2e-16 ***
age 0.025611 0.003922 6.530 6.60e-11 ***
gender 0.706794 0.088404 7.995 1.29e-15 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 3358.4 on 2431 degrees of freedom
Residual deviance: 3246.0 on 2429 degrees of freedom
AIC: 3252
Number of Fisher Scoring iterations: 4まず引数familyには誤差分散の分布の形を指定します。ロジスティック回帰の場合は誤差分散は\(\varepsilon \sim N(0,y(1-y))\)ということで二項分布（ベルヌーイ分布）が指定されます。また，リンク関数は誤差分散の分布の関数の引数として指定する必要があります。ロジスティック回帰の場合はロジット変換をしているため，結果的に引数familyはbinomial(link="logit")となるわけです。 もしここでプロビット回帰をしたい場合には，binomial(link="probit")としたら良いわけですね。
また，当然glm()でも正規分布の普通の重回帰分析を行うことも出来ます。この場合，familyには正規分布を示すgaussianを，リンク関数には恒等関数を表すidentityを指定してあげてください。指定しなくてもデフォルトでそうなっていますが，ここでは明示的に指定しておきます。
Call:
glm(formula = Q1_A ~ age + gender, family = gaussian(link = "identity"),
data = dat)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 18.054531 0.394846 45.726 <2e-16 ***
age 0.070829 0.008116 8.727 <2e-16 ***
gender 1.891169 0.189308 9.990 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for gaussian family taken to be 19.23359)
Null deviance: 50241 on 2431 degrees of freedom
Residual deviance: 46718 on 2429 degrees of freedom
AIC: 14097
Number of Fisher Scoring iterations: 2当然ですが，lm()のときと同じ結果が得られます。
5.4 変数間の関係のグラフィカルモデル
最後に，今後の授業で登場するグラフィカルモデル（あるいは有向非巡回グラフ; Directed acyclic graph [DAG]）の導入をしておきます。といっても難しい事はありません。 単に説明変数と被説明変数の関係性を矢印で表すことで，モデルの見通しを良くするために使うツールです。
回帰分析の例では，genderおよびageによってQ1_Aの値を予測してみました。これをグラフィカルモデルで表すと 図 5.11 のようになります。
このように，グラフィカルモデルでは観測可能な変数を長方形で表し，矢印によって回帰の向きを表します。 また，両方向の矢印は変数間の相関関係を表しています。 重回帰分析では，複数の説明変数が一つの結果変数を説明しようとするため，グラフィカルモデルはこのように複数の変数から一つの変数に向かって矢印がひかれる形になります。
グラフィカルモデルを自由に拡張して，例えば 図 5.12 のように変数間の関係を広げていったものが，パス解析と呼ばれるやつ （ チャプター 7 ） です。 このモデルを分析する場合，矢印一個一個を回帰分析しても良いかもしれませんが，全体として変数間のモデルができているのですから，全部まとめてデータとの適合度などを評価してあげたいところです。ということでパス解析もSEMの一種です。
SEM（第7章）では，このような変数間のグラフィカルモデルをもとに分析用のコードを作成していくことになります。といっても難しいことはないはずです。データを取る時点で変数間の理論的な関係性の仮説は考えているはずですから…
もちろん実際には股下やら体型やらによって最適な椅子の高さは決まるわけですが，手元には「体重」の情報しか無いので，できる範囲で予測しましょう，ということです。↩︎
直線がイメージしづらいかもしれませんが，説明変数が1個の場合の回帰直線が2次元平面に引かれていたように，説明変数が2個の場合は3次元空間の中に一本の直線が引かれます。同様に，説明変数が\(K\)個ならば\(K+1\)次元空間に一本の直線を引くわけです。↩︎
このあたりの展開は「正規方程式」で検索したらすぐ見つかります↩︎
ちなみに機械学習ではone-hot encodingという名で使われるケースもあります。推定できなくなってしまうのは，説明変数の効果が線形和で表される回帰モデルならではの問題なのです。↩︎
回帰係数の検定という観点では差が1である必要すらも無いのですが，回帰係数の解釈を考えるとやはり0/1のコーディングが一番しっくりきます。↩︎
データフレームの列も
$で取り出せるということは，データフレームは全ての要素が「同じ長さのベクトル」のリストである，という見方もできるわけです。リストとして扱うことは多くは無いですが，知っておくとどこかで役立つかもしれません。↩︎内部的には，
summary()で呼び出せる複数の関数が存在しており，与えるオブジェクトのクラスによって異なる関数が実行されています。lm()の出力はlmクラスのオブジェクトであり，これに対してはsummary.lm()が自動的に呼び出されているのです。なのでlmオブジェクトに対するsummary()関数のヘルプを見たい場合には?summary.lmとしてあげる必要があります。↩︎回帰分析モデルでは，これも仮定のひとつとしておかれます。この仮定が守られていない場合，検定結果にバイアスがかかったりするわけです。↩︎
良いモデルを選びたい場合には，決定係数の比較よりも交差検証(cross validation)などを用いるのが良いとされているようです。↩︎
これに対して正規分布の普通の重回帰モデルを一般線形モデル(general linear model)と呼んだりします。↩︎
ロジスティック関数とロジット関数は互いに逆関数の関係になっています。そのため，説明変数側の変換として見た場合にはロジスティック変換と呼ばれる一方で，結果変数側の変換（リンク関数）として見る場合にはロジット変換と呼ばれるわけです（たぶん）。実際に回帰分析としての手法名では「ロジスティック回帰」とも「ロジット回帰」とも呼ばれることがあるはずです。↩︎