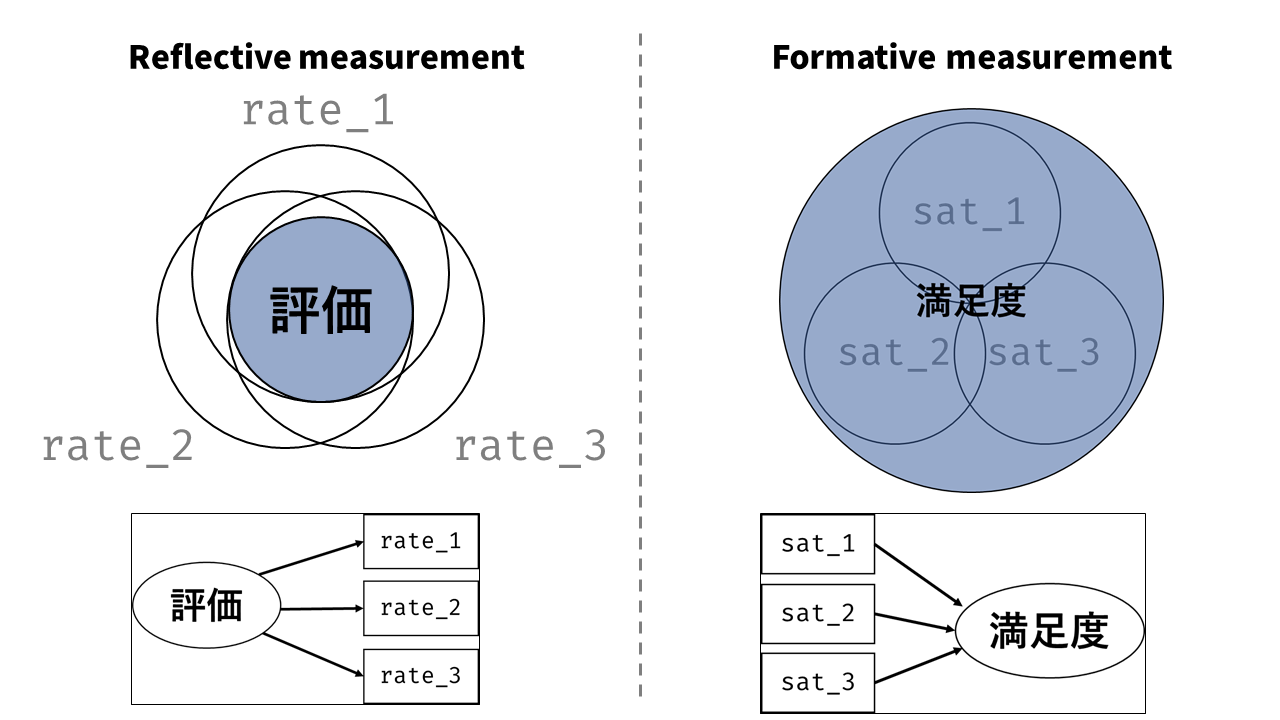
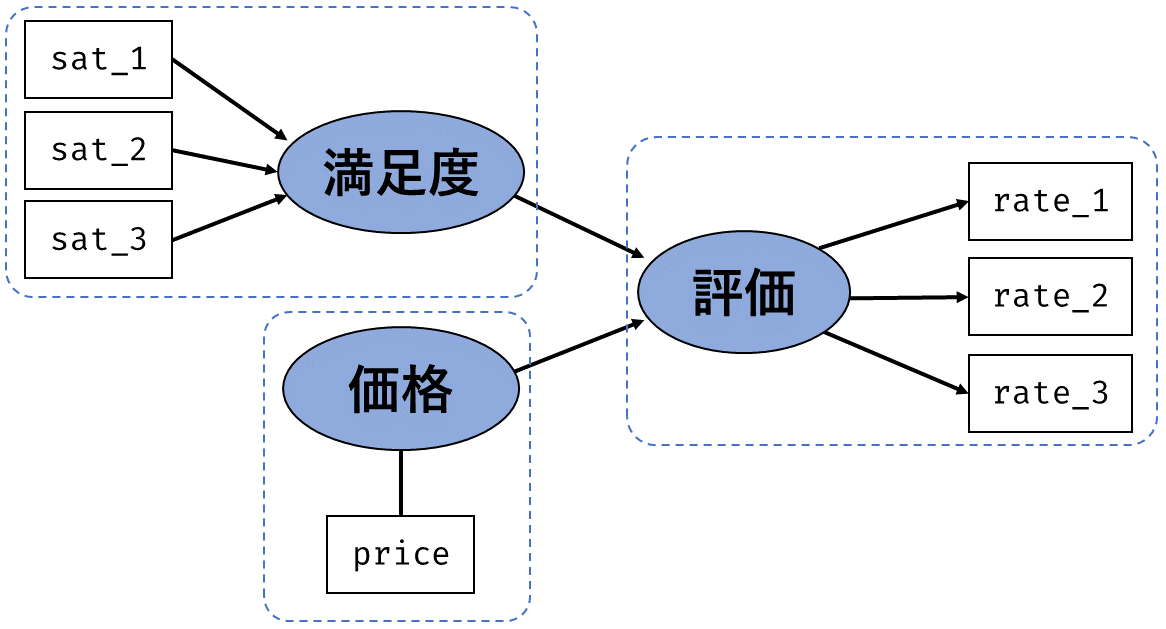
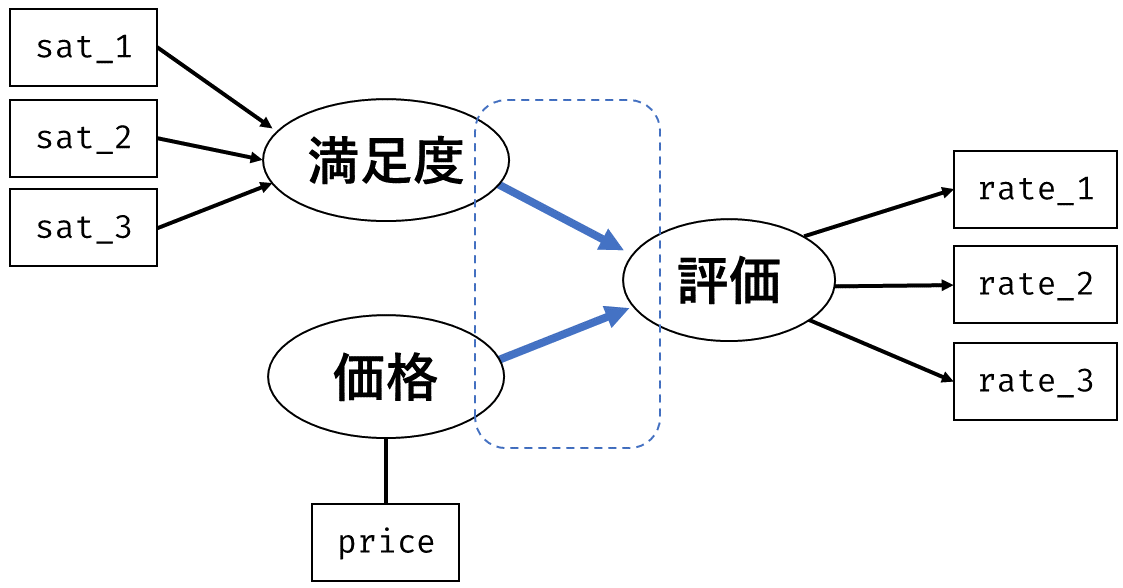
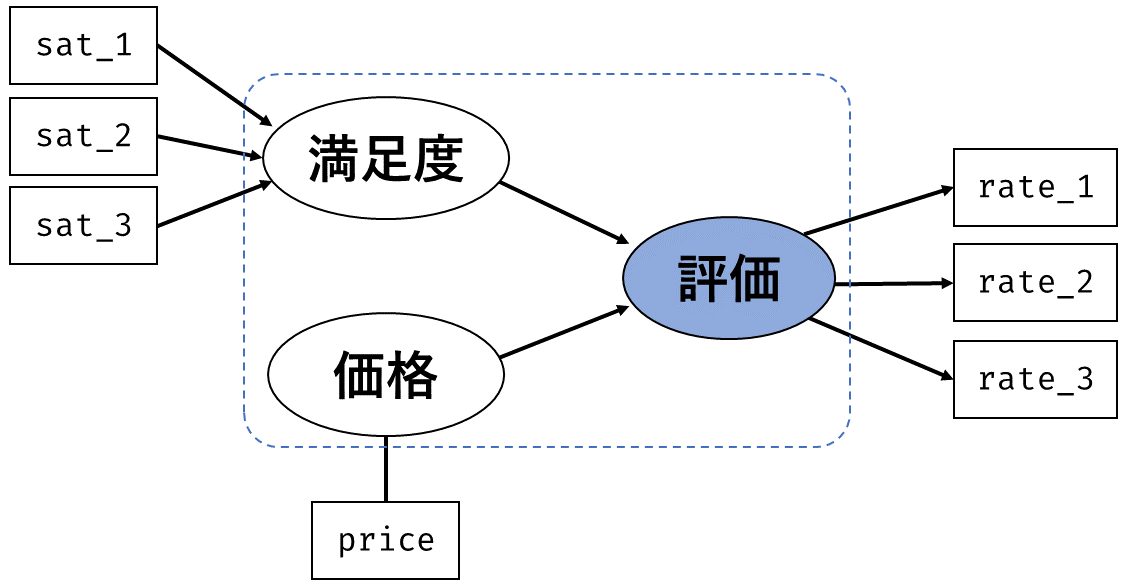
本章の構成
今回からは構造方程式モデリング (Structural Equation Modeling; SEM)の話です。 はじめにSEMの基本的な考え方を紹介し,Rで実際に実行してみます。
RでのSEMはlavaanというパッケージを用いるのが最もメジャーです。 事前にインストール&読み込みをしておきましょう。 合わせて,このチャプターで使用するいくつかのパッケージもインストールしておきます。
↓本Chapterで使用するファイルのダウンロードはこちらから
7.1 因子分析の見方を変える
7.1.1 1因子モデル
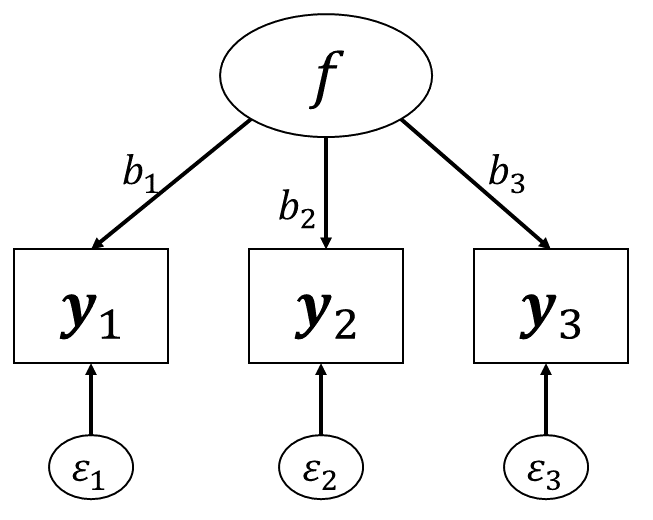
まずは 図 7.1 のような1因子3項目の因子分析モデルを考えてみます。 このモデルでは,各観測変数はそれぞれ \[
\left\{
\begin{aligned}
\symbf{y}_1 &= \symbf{f}b_{1} + \symbf{\varepsilon}_1 \\
\symbf{y}_2 &= \symbf{f}b_{2} + \symbf{\varepsilon}_2 \\
\symbf{y}_3 &= \symbf{f}b_{3} + \symbf{\varepsilon}_3
\end{aligned}
\right.
\tag{7.1}\] と表されました。したがって,3つの観測変数のモデル上の共分散行列\(\symbf{\Sigma}\)は \[
\symbf{\Sigma} = \begin{bmatrix}
b_1^2+\sigma_{\symbf{\varepsilon}_1}^2 & b_1b_2 & b_1b_3\\
b_2b_1 & b_2^2+\sigma_{\symbf{\varepsilon}_2}^2 & b_2b_3\\
b_3b_1 & b_3b_2 & b_3^2+\sigma_{\symbf{\varepsilon}_3}^2
\end{bmatrix}
\tag{7.2}\] となります。 また,3つの観測変数のデータでの共分散行列も \[
\symbf{S} = \begin{bmatrix}
\sigma_{y_1}^2 & \sigma_{y_1,y_2} & \sigma_{y_1,y_3} \\
\sigma_{y_2,y_1} & \sigma_{y_2}^2 & \sigma_{y_2,y_3} \\
\sigma_{y_3,y_1} & \sigma_{y_3,y_2} & \sigma_{y_3}^2
\end{bmatrix}
\tag{7.3}\] と表すことができ,これは実際にデータから計算が可能です。 例えばQ1_1からQ1_3の3項目のみを考えればcov(dat[,paste0("Q1_",1:3)])によって1具体的に \[
\symbf{S} = \begin{bmatrix}
1.976 & 0.581 & 0.504 \\
0.581 & 1.375 & 0.762 \\
0.504 & 0.762 & 1.706
\end{bmatrix}
\] という値が得られます。 構造方程式モデリングでは,\(\symbf{\Sigma}\)の値が\(\symbf{S}\)にできるだけ近づくように母数(パラメータ)を推定します。 実際に(7.2)式の\(\symbf{\Sigma}\)と(7.3)式の\(\symbf{S}\)の同じ項をイコールで結ぶと, \[
\left\{
\begin{aligned}
\sigma_{y_1}^2 &= b_1^2+\sigma_{\symbf{\varepsilon}_1}^2 \\
\sigma_{y_2}^2 &= b_2^2+\sigma_{\symbf{\varepsilon}_2}^2 \\
\sigma_{y_3}^2 &= b_3^2+\sigma_{\symbf{\varepsilon}_3}^2 \\
\sigma_{y_1,y_2} &= b_1b_2\\
\sigma_{y_1,y_3} &= b_1b_3\\
\sigma_{y_2,y_3} &= b_2b_3\\
\end{aligned}
\right.
\tag{7.4}\] という連立方程式を得ることが出来ます。このモデルで推定するべきパラメータは\((b_1,b_2,b_3,\sigma_{\symbf{\varepsilon}_1}^2,\sigma_{\symbf{\varepsilon}_2}^2,\sigma_{\symbf{\varepsilon}_3}^2)\)の6つです。 そして式も6つあるため,このケースでは明確な解を求めることが出来ます。 例えばQ1_1からQ1_3の3項目であれば \[
\left\{
\begin{aligned}
1.976 &= b_1^2+\sigma_{\symbf{\varepsilon}_1}^2 \\
1.375 &= b_2^2+\sigma_{\symbf{\varepsilon}_2}^2 \\
1.706 &= b_3^2+\sigma_{\symbf{\varepsilon}_3}^2 \\
0.581 &= b_1b_2\\
0.504 &= b_1b_3\\
0.762 &= b_2b_3\\
\end{aligned}
\right.
\] となり,これを解くと \[
\left\{
\begin{aligned}
b_1 &= 0.620 \\
b_2 &= 0.937 \\
b_3 &= 0.813 \\
\sigma_{\symbf{\varepsilon}_1}^2 &= 1.591 \\
\sigma_{\symbf{\varepsilon}_2}^2 &= 0.497 \\
\sigma_{\symbf{\varepsilon}_3}^2 &= 1.045
\end{aligned}
\right.
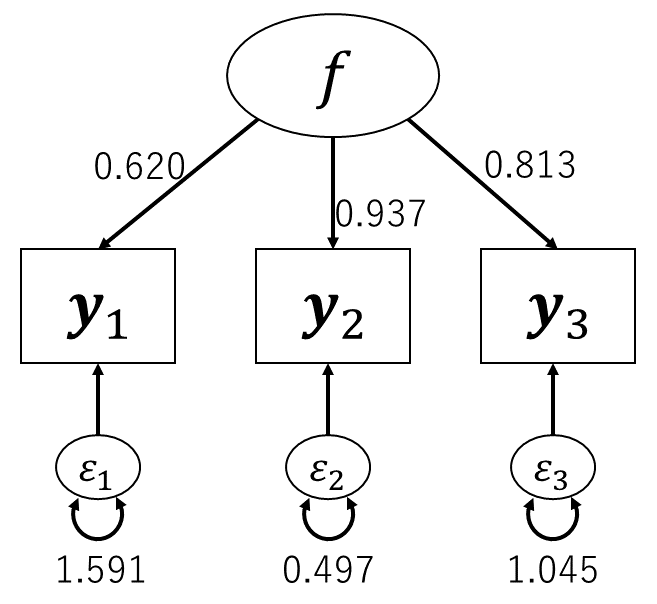
\tag{7.5}\] という解が得られます。 図 7.1 に書き加えたならば 図 7.2 のようになります。
もちろん(7.5)式の値を(7.2)式に代入すれば, \[ \begin{aligned} \symbf{\Sigma} &= \begin{bmatrix} b_1^2+\sigma_{\symbf{\varepsilon}_1}^2 & b_1b_2 & b_1b_3\\ b_2b_1 & b_2^2+\sigma_{\symbf{\varepsilon}_2}^2 & b_2b_3\\ b_3b_1 & b_3b_2 & b_3^2+\sigma_{\symbf{\varepsilon}_3}^2 \end{bmatrix} \\ &= \begin{bmatrix} 0.620^2+1.591 & 0.620\times0.937 & 0.620\times0.813\\ 0.937\times0.620 & 0.937^2+0.497 & 0.937\times0.813\\ 0.813\times0.620 & 0.813\times0.937 & 0.813^2+1.045 \end{bmatrix}\\ &\approx\begin{bmatrix} 1.976 & 0.581 & 0.504 \\ 0.581 & 1.375 & 0.762 \\ 0.504 & 0.762 & 1.706 \end{bmatrix} \\ &= \symbf{S} \end{aligned} \tag{7.6}\] というように,\(\symbf{\Sigma}\)は\(\symbf{S}\)と(丸め誤差を除けば)完全に一致することが確認できます。
グラフィカルモデルでは,観測変数を四角形で,潜在変数を楕円で表していました。 図 7.2 とパラメータの関係を見てみると,2つの観測変数の共分散は,2つの四角形を結ぶ矢印にかかる係数の積になっていることがわかります。 つまり,グラフィカルモデル上で経路が存在する観測変数間には非ゼロの共分散があることを仮定していたわけです。 また,1つの観測変数の分散は,その四角形に向かっている矢印の係数の二乗和になっています。 なお,独自因子には自分自身に対する両方向の矢印が引かれています。 グラフィカルモデルでは両方向の矢印で共分散を表すので,これは自分自身との共分散=分散を表していることになります。
先程の結果は観測変数を標準化していない状態での解でした。 そのため,独自因子の分散が1を超えたり,因子負荷の二乗との合計が1にならなかったりしています。 例えば項目\(\symbf{y}_1\)について見てみると,因子負荷の二乗と独自因子の分散の和は\(0.620^2+1.591\approx1.976\)となります。これは,\(\symbf{y}_1\)の分散\(\sigma_{y_1}^2\)の値1.976に対応しているわけです。 ここで前回までの因子分析と同じように全ての観測変数を標準化した状態,つまり\(\symbf{S}\)に共分散行列ではなく相関行列を与えて推定をした場合に得られる解のことを標準化解や標準化推定値などと呼びます。 そしてSEMでは多くの場合,結果には標準化解を載せています。 絶対のルールでは無いのですが,特に潜在変数がある場合には単位の影響を受けない標準化解を用いたほうがしっくり来る,ということなのでしょう。 ということでこの先も,潜在変数が含まれるモデルを扱う場合には\(\symbf{S}\)には相関行列を想定した,標準化解を考えることにします。
実際に先程の例で標準化解を計算してみると,データにおける相関行列\(\symbf{S}\)はcor(dat[,paste0("Q1_",1:3)])によって具体的に2 \[
\symbf{S} = \begin{bmatrix}
1 & 0.353 & 0.274 \\
0.353 & 1 & 0.497 \\
0.274 & 0.497 & 1
\end{bmatrix}
\] という値が得られるため,連立方程式は \[
\left\{
\begin{aligned}
1 &= b_1^2+\sigma_{\symbf{\varepsilon}_1}^2 \\
1 &= b_2^2+\sigma_{\symbf{\varepsilon}_2}^2 \\
1 &= b_3^2+\sigma_{\symbf{\varepsilon}_3}^2 \\
0.353 &= b_1b_2\\
0.274 &= b_1b_3\\
0.497 &= b_2b_3\\
\end{aligned}
\right.
\] となり,これを解くと \[
\left\{
\begin{aligned}
b_1 &= 0.441 \\
b_2 &= 0.800 \\
b_3 &= 0.622 \\
\sigma_{\symbf{\varepsilon}_1}^2 &= 0.805 \\
\sigma_{\symbf{\varepsilon}_2}^2 &= 0.361 \\
\sigma_{\symbf{\varepsilon}_3}^2 &= 0.613
\end{aligned}
\right.
\] という標準化解を得ることができます。
7.1.2 2因子モデル
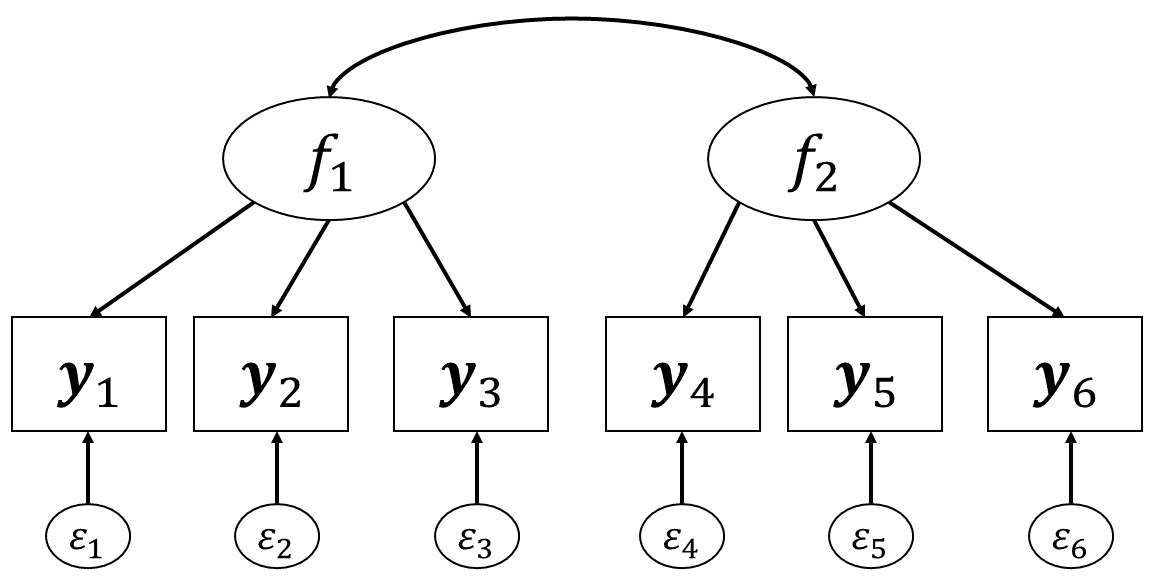
続いて 図 7.3 のような2因子6項目の因子分析モデルで同じように見てみましょう。 ここでは,因子1は最初の3項目にのみ,因子2は後ろの3項目にのみ影響を与えているという仮定を置いています。 また,2つの因子の間は両矢印でつながっています。これは因子間に相関関係\(r_{f1,f2}\)があることを表しています。 このように,(共)分散を表す時には両矢印を使います。 言い換えると,ここでは因子間の共分散(=相関)が0でなくても良いという仮定(斜交回転)を置いているのです。
このモデルでは,因子負荷行列\(\symbf{B}^\top\)は \[ \begin{aligned} \symbf{B}^\top = \begin{bmatrix} b_{11} & 0\\ b_{21} & 0\\ b_{31} & 0\\ 0 & b_{42} \\ 0 & b_{52}\\ 0 & b_{62} \end{bmatrix} \end{aligned} \tag{7.7}\] となります。 ちなみにSEMで多因子モデルを扱う場合の多くは,このように1項目が1因子からのみ影響を受けていると考えると思います3。
すると,6つの観測変数のモデル上の相関行列\(\symbf{\Sigma}\)は \[ \begin{aligned} \begin{split} \symbf{\Sigma} &= \symbf{B}^\top\symbf{\Phi} \symbf{B} + \symbf{\Psi} \\ &= \begin{bmatrix} b_{11} & 0\\ b_{21} & 0\\ b_{31} & 0\\ 0 & b_{42}\\ 0 & b_{52}\\ 0 & b_{62} \end{bmatrix}\begin{bmatrix} 1 & r_{f1,f2} \\ r_{f1,f2} & 1 \end{bmatrix}\begin{bmatrix} b_{11} & b_{21} & b_{31} & 0 & 0 & 0\\ 0 & 0 & 0 & b_{42} & b_{52} & b_{62} \\ \end{bmatrix} + \symbf{\Psi} \\ &= \begin{bmatrix} b_{11}^2 & b_{11}b_{21} & b_{11}b_{31} & r_{f1,f2}b_{11}b_{42} & r_{f1,f2}b_{11}b_{52} & r_{f1,f2}b_{11}b_{62} \\ b_{21}b_{11} & b_{21}^2 & b_{21}b_{31} & r_{f1,f2}b_{21}b_{42} & r_{f1,f2}b_{21}b_{52} & r_{f1,f2}b_{21}b_{62} \\ b_{31}b_{11} & b_{31}b_{21} & b_{31}^2 & r_{f1,f2}b_{31}b_{42} & r_{f1,f2}b_{31}b_{52} & r_{f1,f2}b_{31}b_{62} \\ r_{f1,f2}b_{42}b_{11} & r_{f1,f2}b_{42}b_{21} & r_{f1,f2}b_{42}b_{31} & b_{42}^2 & b_{42}b_{52} & b_{42}b_{62} \\ r_{f1,f2}b_{52}b_{11} & r_{f1,f2}b_{52}b_{21} & r_{f1,f2}b_{52}b_{31} & b_{52}b_{42} & b_{52}^2 & b_{52}b_{62} \\ r_{f1,f2}b_{62}b_{11} & r_{f1,f2}b_{62}b_{21} & r_{f1,f2}b_{62}b_{31} & b_{62}b_{42} & b_{62}b_{52} & b_{62}^2 \end{bmatrix} \\&~~~+ \begin{bmatrix} \sigma_{\symbf{\varepsilon}_1}^2 & 0 & 0 & 0 & 0 & 0 \\ 0 & \sigma_{\symbf{\varepsilon}_2}^2 & 0 & 0 & 0 & 0 \\ 0 & 0 & \sigma_{\symbf{\varepsilon}_3}^2 & 0 & 0 & 0 \\ 0 & 0 & 0 & \sigma_{\symbf{\varepsilon}_4}^2 & 0 & 0 \\ 0 & 0 & 0 & 0 & \sigma_{\symbf{\varepsilon}_5}^2 & 0 \\ 0 & 0 & 0 & 0 & 0 & \sigma_{\symbf{\varepsilon}_6}^2 \end{bmatrix} \\ &=\begin{bmatrix} b_{11}^2 + \sigma_{\symbf{\varepsilon}_1}^2 & b_{11}b_{21} & b_{11}b_{31} & r_{f1,f2}b_{11}b_{42} & r_{f1,f2}b_{11}b_{52} & r_{f1,f2}b_{11}b_{62} \\ b_{21}b_{11} & b_{21}^2 + \sigma_{\symbf{\varepsilon}_2}^2 & b_{21}b_{31} & r_{f1,f2}b_{21}b_{42} & r_{f1,f2}b_{21}b_{52} & r_{f1,f2}b_{21}b_{62} \\ b_{31}b_{11} & b_{31}b_{21} & b_{31}^2 + \sigma_{\symbf{\varepsilon}_3}^2 & r_{f1,f2}b_{31}b_{42} & r_{f1,f2}b_{31}b_{52} & r_{f1,f2}b_{31}b_{62} \\ r_{f1,f2}b_{42}b_{11} & r_{f1,f2}b_{42}b_{21} & r_{f1,f2}b_{42}b_{31} & b_{42}^2 + \sigma_{\symbf{\varepsilon}_4}^2 & b_{42}b_{52} & b_{42}b_{62} \\ r_{f1,f2}b_{52}b_{11} & r_{f1,f2}b_{52}b_{21} & r_{f1,f2}b_{52}b_{31} & b_{52}b_{42} & b_{52}^2 + \sigma_{\symbf{\varepsilon}_5}^2 & b_{52}b_{62} \\ r_{f1,f2}b_{62}b_{11} & r_{f1,f2}b_{62}b_{21} & r_{f1,f2}b_{62}b_{31} & b_{62}b_{42} & b_{62}b_{52} & b_{62}^2 + \sigma_{\symbf{\varepsilon}_6}^2 \end{bmatrix} \end{split} \end{aligned} \tag{7.8}\] となります。
例えばy_1とy_4の繋がりを 図 7.3 で見てみると,y_1 → f_1 → f_2 → y_4という経路になっており,この2変数の共分散はそれぞれの矢印に係る係数の積である\(r_{f1,f2}b_{42}b_{11}\)となっていることがわかります。 もし因子間に相関がなければ,y_1とy_4を結ぶ経路は存在せず,数式的には\(r_{f1,f2}=0\)となることからも,この2変数が完全に無相関であることを意味するようになります。
このモデルの重要なポイントは,分散共分散行列が\(\symbf{B}^\top\symbf{\Phi} \symbf{B} + \symbf{\Psi}\)という形で分解可能だという点は前回までの因子分析と全く同じだという点です。 SEMの枠組みでは,因子負荷行列\(\symbf{B}\)や因子間相関\(\symbf{\Phi}\)に関して要素の値を固定(通常は0に固定)するため,それに応じて観測変数間の共分散の形は変わりますが,違いといえばそれだけです4。 特定の因子が特定の項目にのみ負荷を持っているという仮定は,分析者が仮説などに基づいて行うものです。 そして得られた結果(\(\symbf{\Sigma}\)と\(\symbf{S}\)の乖離度)は,その仮説(に基づく共分散構造)がどの程度妥当そうかを表したものといえます。 そのような意味で,SEMにおける因子分析を検証的(確認的)因子分析(confirmatory factor analysis; CFA)と呼びます。 一方,前回まで行っていた因子分析は,因子構造を探し当てるのが目的だったため探索的因子分析(exploratory factor analysis; EFA)と呼んでいます。
上述のモデルでは,推定するパラメータは全部で13個(6個の因子負荷+6個の誤差分散+1個の因子間相関)あり,対する観測変数間の分散共分散の数が全部で21個(分散が6個+共分散が15個)あります。 ということで1因子3項目の場合のように解を一意に求めることは出来ないのですが,なるべく誤差が小さくなるように全てのパラメータをまとめて推定することは可能なわけです。
7.1.3 もう少しだけ複雑なモデル
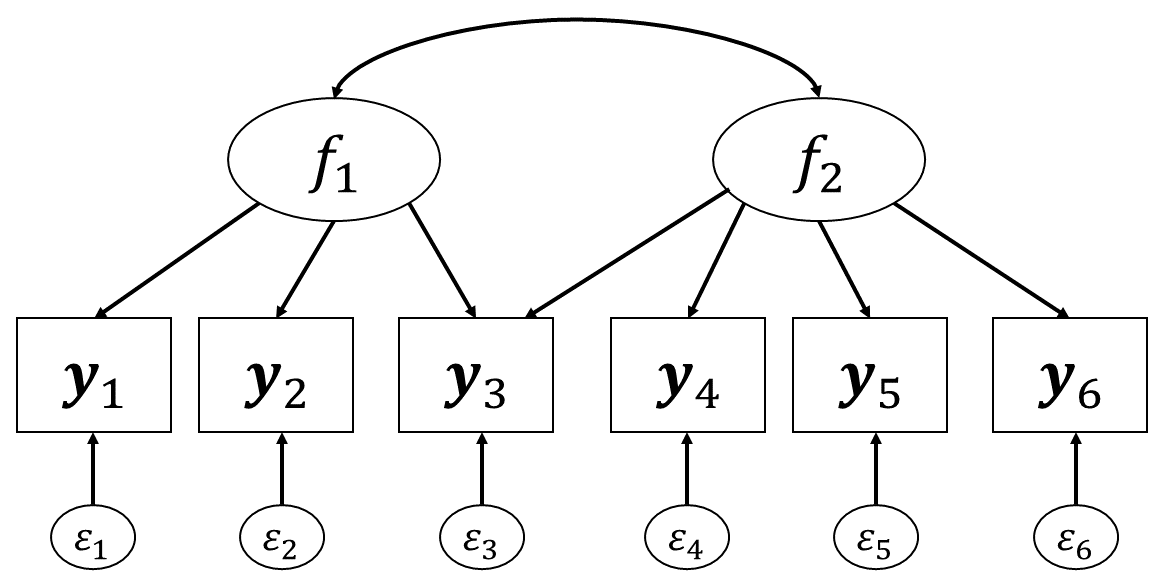
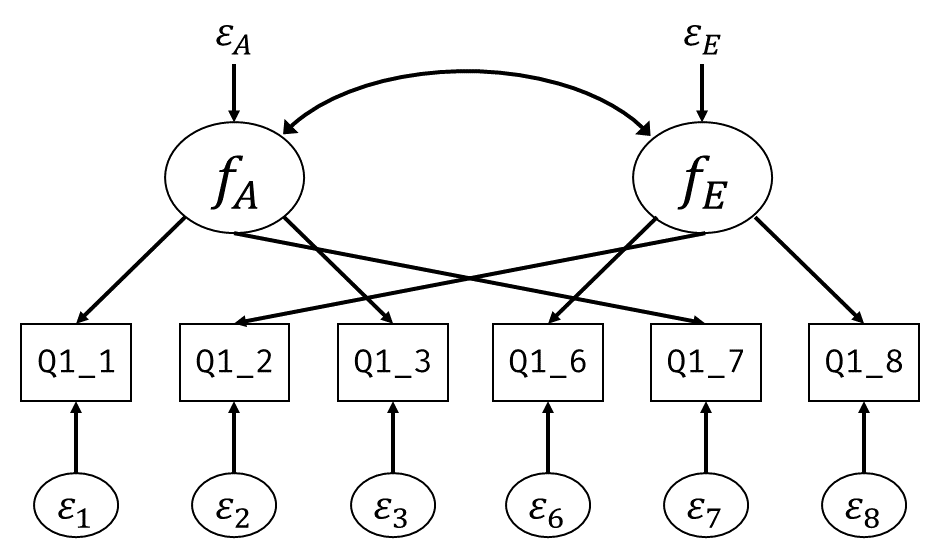
CFAでは,「ある項目は2つの因子の影響を受けている」というモデルを作ることも当然可能です。 図 7.4 は,項目3だけが2つの因子の影響を受けていると仮定しています。 この時,因子負荷行列は \[
\begin{aligned}
\symbf{B}^\top = \begin{bmatrix}
b_{11} & 0\\
b_{21} & 0\\
b_{31} & b_{32}\\
0 & b_{42} \\
0 & b_{52}\\
0 & b_{62}
\end{bmatrix}
\end{aligned}
\tag{7.9}\] となります。このとき共分散行列はどうなるでしょうか。 (7.8)式と同じ要領で\(\symbf{\Sigma}\)は計算できるのですが,すべて書くのは面倒ですね。 例えば項目1と3の共分散だけ抜き出してみると \[
\sigma_{y1, y3} = b_{31}b_{11} + r_{f1,f2}b_{32}b_{11}
\tag{7.10}\] という形になっています。 改めて 図 7.4 でy_1とy_3の経路を見てみると,
y_1→f_1→y_3(\(b_{31}b_{11}\))y_1→f_1→f_2→y_3(\(r_{f1,f2}b_{32}b_{11}\))
という2つの経路が存在しており,それに対応した係数の積の和がこの2変数の共分散を表すようになっています。 また,項目3の分散は \[ \sigma_{y3}^2 = b_{31}^2 + b_{32}^2 + 2r_{f1,f2}b_{31}b_{32} + \sigma_{\symbf{\varepsilon}_3}^2 \tag{7.11}\] となります。1因子モデルのときも分散は係数の二乗和になっていましたが,より正確に言えば
y_3→f_1→y_3(\(b_{31}^2\))y_3→f_2→y_3(\(b_{32}^2\))y_3→e_3→y_3(\(\sigma_{\symbf{\varepsilon}_3}^2\))y_3→f_1→f_2→y_3(\(r_{f1,f2}b_{31}b_{32}\))y_3→f_2→f_1→y_3(\(r_{f1,f2}b_{31}b_{32}\))
という要領で,その変数を出発してから戻るまでの経路の全パターンに関して同様の計算をしていたわけです。
SEMにおいて2つの観測変数の共分散がモデル上でどのように表現されるかの考え方は,Wright’s tracing rulesとして知られています(Wright, 1934)。 これは,以下の3つのシンプルなルールによって表されます(Loehlin & Beaujean, 2016)。
- ループの禁止 (No loops):同じ変数を通過して元の場所に戻ったり、同じ変数を二度経由してはならない。
- 逆流の禁止 (No going forward then backward):一度矢印の向きに従って進んだら(順方向),その経路内で矢印を遡る動き(逆方向)をしてはいけない。
- 双方向矢印の制限 (A maximum of one curved arrow per path):双方向の矢印(共分散・相関)は、1つの経路につき1回しか通れない。
特に潜在変数が絡む因子分析のようなモデルでは,上記のルールを満たしながら考えることができる観測変数間の経路を全て列挙し,その経路にかかる係数の積を計算していくわけです。
7.2 Rでやってみる(検証的因子分析)
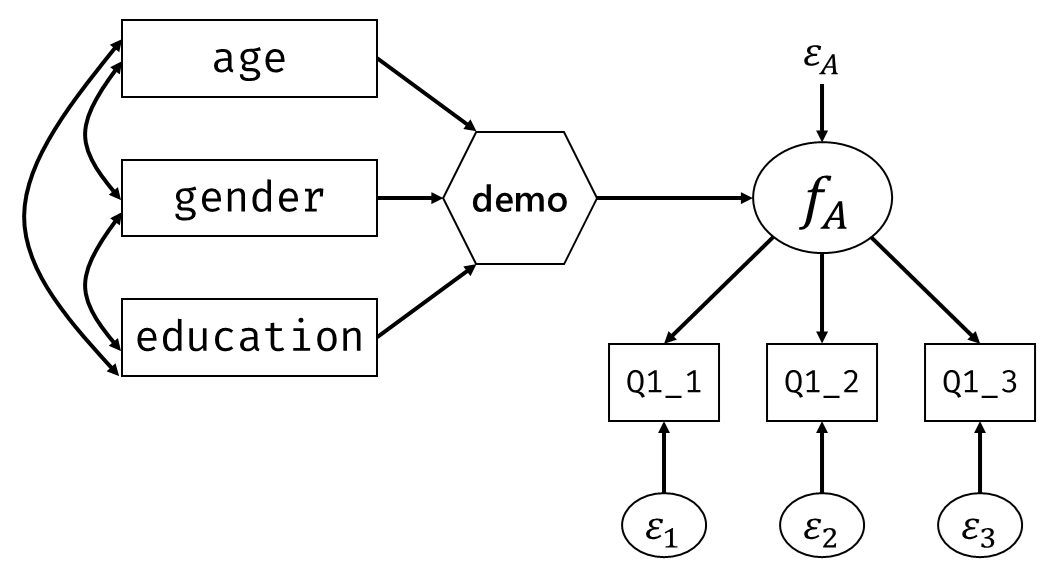
それでは, 図 7.3 の2因子モデルを実際にSEMの枠組み(検証的因子分析)で推定してみましょう。 lavaanでは,lm()などと同じように第一引数にモデル式を与えます。 ただ複雑なモデルになると結構な長さになるので,以下のように事前にモデル式をオブジェクトに入れておくのがおすすめです。
モデル式はcharacter型で用意するため,ダブルクオート(" ")かシングルクオート(' ')で全体をくくります。 その中に,回帰式のようなものを書き連ねていきます。 lavaanの構文では,潜在変数を規定する場合にはイコールチルダ(=~)を使用します。 つまり,上のコードの4行目では「因子f_1はQ1_1とQ1_2とQ1_3に影響を与えているもの」であることを表しているわけです。 ちなみに観測変数に関してはデータフレームの列名で指定しますが,潜在変数はデータフレーム内に存在しないので,自分でわかりやすい名前をつけても構いません。 例えばQ1_1とQ1_2とQ1_3は”Agreeableness”を測定する項目だとわかっているので,1行目はf_A =~ Q1_1 + Q1_2 + Q1_3としても良いわけです。 lavaanでは,データフレームに存在しない変数は自動的に潜在変数であるとみなして分析を行ってくれます。
モデル式が用意できたら,あとは分析を実行するだけです。 検証的因子分析の場合にはcfa()という関数を利用しましょう5。
lavaan 0.6-20 ended normally after 38 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 13
Number of observations 2432
Model Test User Model:
Test statistic 62.061
Degrees of freedom 8
P-value (Chi-square) 0.000
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|)
f_1 =~
Q1_1 1.000
Q1_2 1.548 0.106 14.538 0.000
Q1_3 1.348 0.082 16.362 0.000
f_2 =~
Q1_6 1.000
Q1_7 1.220 0.075 16.316 0.000
Q1_8 0.894 0.053 16.756 0.000
Covariances:
Estimate Std.Err z-value P(>|z|)
f_1 ~~
f_2 0.115 0.016 7.349 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.Q1_1 1.607 0.051 31.229 0.000
.Q1_2 0.492 0.054 9.151 0.000
.Q1_3 1.036 0.050 20.917 0.000
.Q1_6 0.950 0.043 22.233 0.000
.Q1_7 0.888 0.055 16.193 0.000
.Q1_8 1.205 0.044 27.532 0.000
f_1 0.368 0.040 9.180 0.000
f_2 0.567 0.047 11.995 0.000結果を上から見ていきましょう。
Estimatorのところで,最尤推定法(ML)によってパラメータを求めていることがわかります。 パラメータは反復計算で求めているのですが,Optimization methodはその計算アルゴリズムを示しています。基本的には触れなくてOKです。 Number of model parametersはモデルのパラメータ数です。6個の因子負荷+6個の誤差分散+1個の因子間相関で13個ということは先程説明した通りです。
モデルに対して\(\chi^2\)検定を行っています。 帰無仮説は「モデルの共分散行列とデータの共分散行列が同じ」ということで,\(p\)値が大きい(帰無仮説が棄却されない)ほど当てはまりが良いことを意味します。 つまり,できればこの検定は棄却されない(\(p>.05\))と嬉しいのですが,統計的仮説検定の仕組み上サンプルサイズが多いほど帰無仮説が棄却されやすかったりとなかなか使い勝手の良いものではないので,基本的には無視でも良いでしょう。
因子負荷です。 lavaanはデフォルトでは,パラメータの制約として「因子の分散が1」の代わりに「各因子の第1項目に対する因子負荷が1」という制約を置いています。 因子分析の資料の3ページで潜在変数のスケールの不定性を説明しましたが,lavaanのデフォルトでは因子ごとに最初の項目の\(b\)の値を一つ固定することによってその不定性を封じているわけです。 ですが一般的には「因子の分散が1」の方がよく用いられる制約なので,そのようにした場合の推定値も出力してみます。 その方法は2種類あり,1つ目の方法は「推定時に引数std.lv = TRUEを与える」というものです。
lavaan 0.6-20 ended normally after 27 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 13
Number of observations 2432
Model Test User Model:
Test statistic 62.061
Degrees of freedom 8
P-value (Chi-square) 0.000
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|)
f_1 =~
Q1_1 0.607 0.033 18.359 0.000
Q1_2 0.939 0.034 27.729 0.000
Q1_3 0.818 0.034 24.120 0.000
f_2 =~
Q1_6 0.753 0.031 23.990 0.000
Q1_7 0.919 0.035 26.112 0.000
Q1_8 0.673 0.031 21.419 0.000
Covariances:
Estimate Std.Err z-value P(>|z|)
f_1 ~~
f_2 0.251 0.028 8.852 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.Q1_1 1.607 0.051 31.229 0.000
.Q1_2 0.492 0.054 9.151 0.000
.Q1_3 1.036 0.050 20.917 0.000
.Q1_6 0.950 0.043 22.233 0.000
.Q1_7 0.888 0.055 16.193 0.000
.Q1_8 1.205 0.044 27.532 0.000
f_1 1.000
f_2 1.000 std.lv = TRUEとすることで,潜在変数(latent variable)を標準化(standardized)することができます。 また,もう一つの方法は「summary()時に引数standardized = TRUEを与える」というものです。 この方法では因子の分散を1に調整した場合の推定値を事後的に変換して出力してくれます。
lavaan 0.6-20 ended normally after 38 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 13
Number of observations 2432
Model Test User Model:
Test statistic 62.061
Degrees of freedom 8
P-value (Chi-square) 0.000
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_1 =~
Q1_1 1.000 0.607 0.432
Q1_2 1.548 0.106 14.538 0.000 0.939 0.801
Q1_3 1.348 0.082 16.362 0.000 0.818 0.626
f_2 =~
Q1_6 1.000 0.753 0.611
Q1_7 1.220 0.075 16.316 0.000 0.919 0.698
Q1_8 0.894 0.053 16.756 0.000 0.673 0.523
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_1 ~~
f_2 0.115 0.016 7.349 0.000 0.251 0.251
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Q1_1 1.607 0.051 31.229 0.000 1.607 0.814
.Q1_2 0.492 0.054 9.151 0.000 0.492 0.358
.Q1_3 1.036 0.050 20.917 0.000 1.036 0.608
.Q1_6 0.950 0.043 22.233 0.000 0.950 0.626
.Q1_7 0.888 0.055 16.193 0.000 0.888 0.513
.Q1_8 1.205 0.044 27.532 0.000 1.205 0.727
f_1 0.368 0.040 9.180 0.000 1.000 1.000
f_2 0.567 0.047 11.995 0.000 1.000 1.000引数standardized = TRUEを与えると,係数の出力の右にStd.lvとStd.allという2つの列が追加されます。 Std.lv列は,推定時に引数std.lv = TRUEを与えた時と同じ「潜在変数のみ標準化された場合」の推定値です。 一方Std.all列はその名の通り「観測変数も含めて全て標準化された場合」の推定値,すなわち標準化解を出しています。
ただ実際の推定時には,std.lv = TRUEをいれると同時に,summary()時にstandardized = TRUEを入れるようにすると良いのではないかと思います。 というのもcfa(std.lv = TRUE)のみだと観測変数まで標準化した標準化解が出力されません。 一方summary(standardized = TRUE)のみだと各因子の第1項目の因子負荷が推定されなくなるため,仮説検定を行ってくれないためです。
ということで改めて因子負荷から見ていきます。
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_1 =~
Q1_1 0.607 0.033 18.359 0.000 0.607 0.432
Q1_2 0.939 0.034 27.729 0.000 0.939 0.801
Q1_3 0.818 0.034 24.120 0.000 0.818 0.626
f_2 =~
Q1_6 0.753 0.031 23.990 0.000 0.753 0.611
Q1_7 0.919 0.035 26.112 0.000 0.919 0.698
Q1_8 0.673 0.031 21.419 0.000 0.673 0.523左から「推定値」「標準誤差」「検定統計量\(z\)」「\(p\)値」「Std.lv」「Std.all」と並んでいます。 回帰分析のときと同じように「因子負荷が0」という帰無仮説に対して仮説検定を行っています。 検定の結果は標準化してもしなくても変わらないのでご安心ください。
共分散です。Std.lvとStd.allでは潜在変数の分散は1になっているため,ここに表示されている0.251は2因子の因子間相関を表しています。
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Q1_1 1.607 0.051 31.229 0.000 1.607 0.814
.Q1_2 0.492 0.054 9.151 0.000 0.492 0.358
.Q1_3 1.036 0.050 20.917 0.000 1.036 0.608
.Q1_6 0.950 0.043 22.233 0.000 0.950 0.626
.Q1_7 0.888 0.055 16.193 0.000 0.888 0.513
.Q1_8 1.205 0.044 27.532 0.000 1.205 0.727
f_1 1.000 1.000 1.000
f_2 1.000 1.000 1.000各変数の分散です。Std.lvとStd.allでは一番下の2つ(f_1とf_2)の分散は1に固定されています。 変数名の左に.がついているものは,その観測変数にくっつく独自因子の分散(または誤差分散)を表しています。
独自因子の分散のなかでもStd.all列に表示された値は,探索的因子分析と同じように独自性の値として考えることが出来ます。 例えば項目Q1_1では,Std.allの値=独自因子の分散が0.814です。これに対して因子負荷は0.432でした。 実際に因子負荷の二乗と独自因子の分散の和は\(0.432^2+0.814\approx1\)となります。
実際にcfa()関数によって推定されたパラメータの値(Std.all)を,(7.8)式に代入して\(\symbf{\Sigma}\)を計算してみましょう(添字の項目番号はデータに合わせて変えています)。
\[ \begin{aligned} \symbf{\Sigma} &= \symbf{B}^\top\symbf{\Phi} \symbf{B} + \symbf{\Psi} \\ &=\begin{bmatrix} b_{11}^2 + \sigma_{\symbf{\varepsilon}_1}^2 & b_{11}b_{21} & b_{11}b_{31} & r_{f1,f2}b_{11}b_{62} & r_{f1,f2}b_{11}b_{72} & r_{f1,f2}b_{11}b_{82} \\ b_{21}b_{11} & b_{21}^2 + \sigma_{\symbf{\varepsilon}_2}^2 & b_{21}b_{31} & r_{f1,f2}b_{21}b_{62} & r_{f1,f2}b_{21}b_{72} & r_{f1,f2}b_{21}b_{82} \\ b_{31}b_{11} & b_{31}b_{21} & b_{31}^2 + \sigma_{\symbf{\varepsilon}_3}^2 & r_{f1,f2}b_{31}b_{62} & r_{f1,f2}b_{31}b_{72} & r_{f1,f2}b_{31}b_{82} \\ r_{f1,f2}b_{62}b_{11} & r_{f1,f2}b_{62}b_{21} & r_{f1,f2}b_{62}b_{31} & b_{62}^2 + \sigma_{\symbf{\varepsilon}_6}^2 & b_{62}b_{72} & b_{62}b_{82} \\ r_{f1,f2}b_{72}b_{11} & r_{f1,f2}b_{72}b_{21} & r_{f1,f2}b_{72}b_{31} & b_{72}b_{62} & b_{72}^2 + \sigma_{\symbf{\varepsilon}_7}^2 & b_{72}b_{82} \\ r_{f1,f2}b_{82}b_{11} & r_{f1,f2}b_{82}b_{21} & r_{f1,f2}b_{82}b_{31} & b_{82}b_{62} & b_{82}b_{72} & b_{82}^2 + \sigma_{\symbf{\varepsilon}_8}^2 \end{bmatrix} \\ &=\begin{bmatrix} 0.432^2 + 0.814 & 0.432\times0.801 & 0.432\times0.626 & 0.251\times0.432\times0.611 & 0.251\times0.432\times0.698 & 0.251\times0.432\times0.523 \\ 0.801\times0.432 & 0.801^2 + 0.358 & 0.801\times0.626 & 0.251\times0.801\times0.611 & 0.251\times0.801\times0.698 & 0.251\times0.801\times0.523 \\ 0.626\times0.432 & 0.626\times0.801 & 0.626^2 + 0.608 & 0.251\times0.626\times0.611 & 0.251\times0.626\times0.698 & 0.251\times0.626\times0.523 \\ 0.251\times0.611\times0.432 & 0.251\times0.611\times0.801 & 0.251\times0.611\times0.626 & 0.611^2 + 0.626 & 0.611\times0.698 & 0.611\times0.523 \\ 0.251\times0.698\times0.432 & 0.251\times0.698\times0.801 & 0.251\times0.698\times0.626 & 0.698\times0.611 & 0.698^2 + 0.513 & 0.698\times0.523 \\ 0.251\times0.523\times0.432 & 0.251\times0.523\times0.801 & 0.251\times0.523\times0.626 & 0.523\times0.611 & 0.523\times0.698 & 0.523^2 + 0.727 \end{bmatrix} \\ &\approx\begin{bmatrix} 1 & 0.346 & 0.270 & 0.066 & 0.076 & 0.057 \\ 0.346 & 1 & 0.501 & 0.123 & 0.140 & 0.105 \\ 0.270 & 0.501 & 1 & 0.096 & 0.110 & 0.082 \\ 0.066 & 0.123 & 0.096 & 1 & 0.426 & 0.320 \\ 0.076 & 0.140 & 0.110 & 0.426 & 1 & 0.365 \\ 0.057 & 0.105 & 0.082 & 0.320 & 0.365 & 1 \end{bmatrix} \end{aligned} \]
そして,cor()関数でデータの相関行列\(\symbf{S}\)を出力してみると以下のようになります。
ということで,モデルから計算された相関行列\(\symbf{\Sigma}\)と,実際のデータの相関行列\(\symbf{S}\)の差を取ると, \[ \symbf{\Sigma}-\symbf{S} = \begin{bmatrix} 0 & -0.007 & -0.004 & 0.077 & 0.087 & 0.033 \\ -0.007 & 0 & 0.004 & 0.025 & 0.016 & -0.080 \\ -0.004 & 0.004 & 0 & -0.014 & -0.032 & -0.044 \\ 0.077 & 0.025 & -0.014 & 0 & -0.009 & 0.007 \\ 0.087 & 0.016 & -0.032 & -0.009 & 0 & 0.006 \\ 0.033 & -0.080 & -0.044 & 0.007 & 0.006 & 0 \end{bmatrix} \tag{7.12}\] と,多くの要素が0に近い値になっていることがわかります。 これは,モデルによってデータの共分散構造がかなり良く再現されていることを意味します。 一方で,もしも\(\symbf{\Sigma}-\symbf{S}\)の値が大きくなってしまう場合には,そもそもモデルの構造自体がデータに合っていないために,頑張って「\(\symbf{\Sigma}\)と\(\symbf{S}\)ができるだけ近い値になるように」パラメータを推定しても,あまり良い結果が得られなかった可能性が高いのです。
ということでSEMでは,推定したパラメータをもとに復元したモデル上の共分散行列\(\symbf{\Sigma}\)と,データにおいて観測された実際の共分散行列\(\symbf{S}\)がきちんと近い値になっているかの確認が非常に重要になります(詳細は セクション 7.6 で)。
ちなみに因子得点は,predict()関数によって出すことが出来ます。
探索的因子分析のときと同様に,この因子得点の相関はモデル上の因子間相関(今回の場合0.251)とは異なります。利用する際は気をつけてください。
7.3 回帰分析の見方を変える
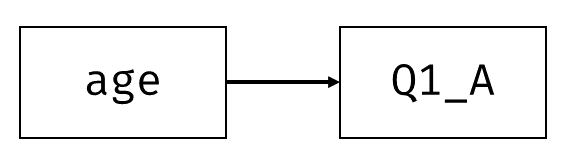
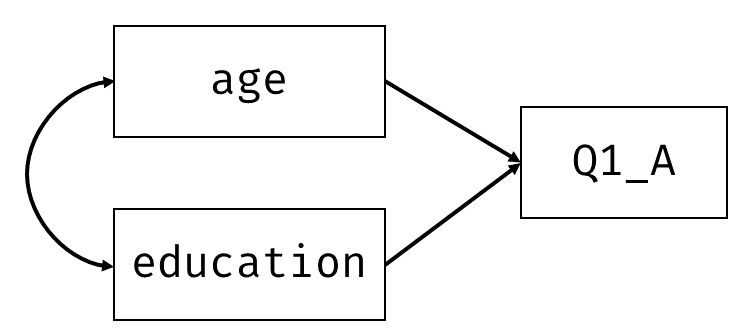
SEMでは回帰分析も共通の枠組みで取り扱うことが出来ます。つまり観測変数間の共分散構造をモデルのパラメータで表し,推定を行います。 最もシンプルな回帰モデルとして, 図 7.5 のように協調性の得点Q1_Aを年齢ageで回帰してみましょう。
このモデルの回帰式は \[ x_A = b_0 + b_1x_{\mathrm{age}} + \varepsilon_A \tag{7.13}\] となります。したがって,この2変数の共分散行列は \[ \symbf{\Sigma} = \begin{bmatrix} \sigma_{x_{A}}^2 & \sigma_{x_A, x_{\mathrm{age}}}\\ \sigma_{x_A, x_{\mathrm{age}}} & \sigma_{x_{\mathrm{age}}}^2 \end{bmatrix} = \begin{bmatrix} b_1^2 \sigma_{x_{\mathrm{age}}}^2+ \sigma_{\varepsilon_A}^2 & b_1\sigma_{x_{\mathrm{age}}}^2 \\ b_1\sigma_{x_{\mathrm{age}}}^2 & \sigma_{x_{\mathrm{age}}}^2 \end{bmatrix} \tag{7.14}\] と表せます。 回帰モデルなので,変数\(x_A\)は\(x_{\mathrm{age}}\)の値に応じて変化していると見ることも出来ます。 言い換えると,\(x_A\)の値はモデルの中で決まっているということです。 このように,モデル式の中で他の変数の関数によって表される変数のことを内生変数(endogenous variable)と呼びます。 一方,変数\(x_{\mathrm{age}}\)は他の変数の値によって変化することはありません。こうした変数を,内生変数に対して外生変数(exogenous variable)と呼びます。 グラフィカルモデル的には,他の変数からの一方向矢印が一つでも刺さっているものは全て内生変数と呼びます。 SEMではこの「内生変数」と「外生変数」の分類がちょくちょく出てくるので,覚えておいてください。
さて,先程の回帰モデルをSEMで見た場合,推定しないといけないパラメータは\(b_1\)と\(\sigma_{\varepsilon_A}^2\)の2つです(\(\sigma_{x_{\mathrm{age}}}^2\)はデータから直接求めたら良いので)。 そしてデータからは(cov()関数を使えば)2つの変数の分散および共分散 \[
\symbf{S} = \begin{bmatrix}
s_{x_{A}}^2 & s_{x_A, x_{\mathrm{age}}}\\
s_{x_A, x_{\mathrm{age}}} & s_{x_{\mathrm{age}}}^2
\end{bmatrix}= \begin{bmatrix}
20.667 & 8.906\\
8.906 & 120.303
\end{bmatrix}
\] の(上三角と下三角は同じ式なので)計3つが計算できるため,これでモデルのパラメータが推定できます。 一応連立方程式を立ててみると, \[
\left\{
\begin{aligned}
20.667 &= b_1^2 \sigma_{x_{\mathrm{age}}}^2+ \sigma_{\varepsilon_A}^2 \\
8.906 &= b_1\sigma_{x_{\mathrm{age}}}^2 \\
120.303 &= \sigma_{x_{\mathrm{age}}}^2
\end{aligned}
\right\} = \left\{\begin{aligned}
20.667 &= 120.303b_1^2+ \sigma_{\varepsilon_A}^2 \\
8.906 &= 120.303b_1
\end{aligned}\right\}
\] となります。このように,外生変数の分散が連立方程式に含まれる場合には,その外生変数のデータでの分散をそのまま入れてあげることが出来ます。 なお,共分散構造のみを扱うならば,切片\(b_0\)は推定の対象になっていないという点には気をつけてください。 切片もモデルの推定対象にしたい場合には,平均構造も含めたSEMを実行する必要があります6。
実際に計算してみると,\((b_1, \sigma_{\varepsilon_A}^2)=(0.074, 20.007)\)という値が得られます。これを\(\symbf{\Sigma}\)にあてはめてみると, \[ \symbf{\Sigma} = \begin{bmatrix} 0.074^2 \times 120.303 + 20.007 & \\ 0.074 \times 120.303 & 120.303 \end{bmatrix} \approx \begin{bmatrix} 20.667 & \\ 8.906 & 120.303 \end{bmatrix} \] ということで,データの共分散行列\(\symbf{S}\)に一致する値が得られました。
7.3.1 もう少し複雑なモデル(パス解析)
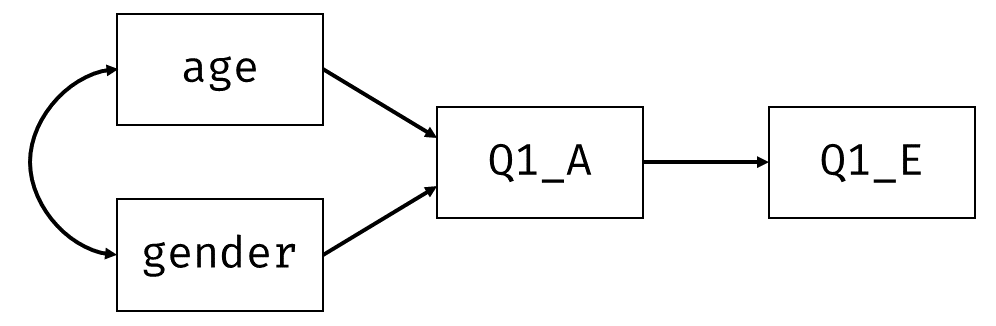
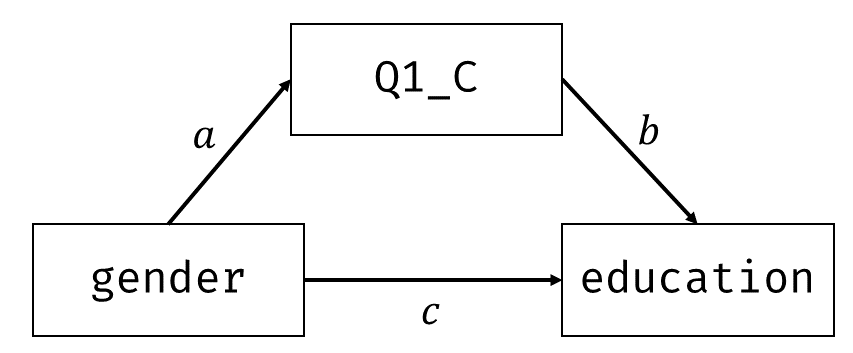
モデルが複雑になってもやることは同じです。回帰式を順に展開していき,全ての変数の分散共分散を「外生変数の分散とパラメータ」で表してあげます。 例えば 図 7.6 は重回帰分析に単回帰分析をくっつけたようなモデルです。 ちなみにこのように,単一の回帰式で表せないような,回帰分析をくっつけたモデルは,SEMの中でも特にパス解析(path analysis)と呼ばれることがあります。
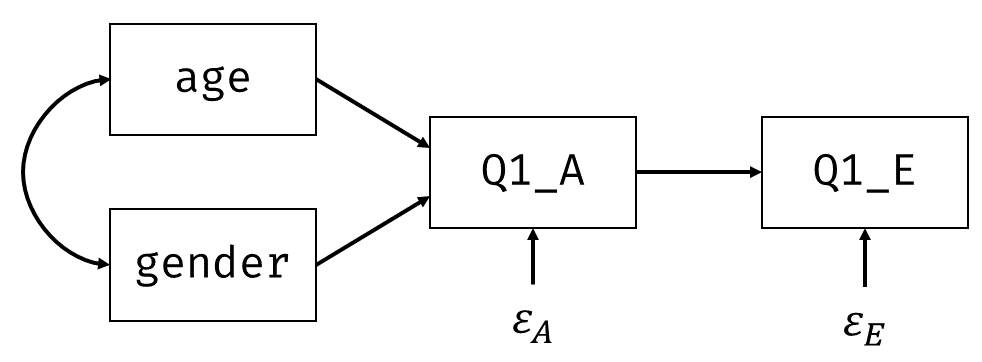
回帰式はそれぞれ \[ \left\{\begin{aligned} x_A &= b_{0A} + b_{\mathrm{gender}}x_{\mathrm{gender}} + b_{\mathrm{age}}x_{\mathrm{age}} + \varepsilon_A \\ x_E &= b_{0E} + b_{A}x_{A} + \varepsilon_E \end{aligned}\right. \tag{7.15}\] となりますが,さらに下の式の\(x_{A}\)を展開することで \[ \left\{\begin{aligned} x_A &= b_{\mathrm{gender}}x_{\mathrm{gender}} + b_{\mathrm{age}}x_{\mathrm{age}} + b_{0A} + \varepsilon_A \\ x_E &= b_{A}\left(b_{0A} + b_{\mathrm{gender}}x_{\mathrm{gender}} + b_{\mathrm{age}}x_{\mathrm{age}} + \varepsilon_A\right) + b_{0E} + \varepsilon_E \\ &= b_{A}b_{0A} + b_{A}b_{\mathrm{gender}}x_{\mathrm{gender}} + b_{A}b_{\mathrm{age}}x_{\mathrm{age}} + b_{A}\varepsilon_A + b_{0E} + \varepsilon_E \end{aligned}\right. \tag{7.16}\] となります。 なお,検証的因子分析での独自因子と同じように,パス解析でも内生変数に誤差項を明示することがあります( 図 7.7 )7。 こうすることによって,各変数の分散および共分散を考えるのが多少楽になります(後述)。
4つの変数のモデル上の共分散行列\(\symbf{\Sigma}\)の各成分は,頑張って展開すると \[ \left\{ \begin{aligned} \sigma_{x_{\mathrm{age}}}^2 &= \sigma_{x_{\mathrm{age}}}^2 \\ \sigma_{x_{\mathrm{gender}}}^2 &= \sigma_{x_{\mathrm{gender}}}^2 \\ \sigma_{x_{\mathrm{gender}}, x_{\mathrm{age}}} &= \sigma_{x_{\mathrm{gender}}, x_{\mathrm{age}}} \\ \sigma_{x_{A}}^2 &= b_{\mathrm{gender}}^2\sigma_{x_{\mathrm{gender}}}^2 + b_{\mathrm{age}}^2\sigma_{x_{\mathrm{age}}}^2 + 2b_{\mathrm{gender}}b_{\mathrm{age}}\sigma_{x_{\mathrm{gender}}, x_{\mathrm{age}}} + \sigma_{\varepsilon_{A}}^2 \\ \sigma_{x_{E}}^2 &= b_{A}^2b_{\mathrm{gender}}^2\sigma_{x_{\mathrm{gender}}}^2 + b_{A}^2b_{\mathrm{age}}^2\sigma_{x_{\mathrm{age}}}^2 + 2b_{A}^2b_{\mathrm{gender}}b_{\mathrm{age}}\sigma_{x_{\mathrm{gender}}, x_{\mathrm{age}}}+b_A^2\sigma_{\varepsilon_{A}}^2+ \sigma_{\varepsilon_{E}}^2 \\ \sigma_{x_{A}, x_{\mathrm{age}}} &= b_{\mathrm{gender}}\sigma_{x_{\mathrm{gender}}, x_{\mathrm{age}}} + b_{\mathrm{age}}\sigma_{x_{\mathrm{age}}}^2 \\ \sigma_{x_{E}, x_{\mathrm{age}}} &= b_{A}b_{\mathrm{gender}}\sigma_{x_{\mathrm{age}},x_{\mathrm{gender}}} + b_{A}b_{\mathrm{age}}\sigma_{x_{\mathrm{age}}}^2 \\ \sigma_{x_{A}, x_{\mathrm{gender}}} &= b_{\mathrm{gender}}\sigma_{x_{\mathrm{gender}}}^2 + b_{\mathrm{age}}\sigma_{x_{\mathrm{age}},x_{\mathrm{gender}}} \\ \sigma_{x_{E}, x_{\mathrm{gender}}} &= b_{A}b_{\mathrm{gender}}\sigma_{x_{\mathrm{gender}}}^2 + b_{A}b_{\mathrm{age}}\sigma_{x_{\mathrm{age}},x_{\mathrm{gender}}}\\ \sigma_{x_{E}, x_{A}} &= b_{A}b_{\mathrm{gender}}^2\sigma_{x_{\mathrm{gender}}}^2 + b_{A}b_{\mathrm{age}}^2\sigma_{x_{\mathrm{age}}}^2 + 2b_{A}b_{\mathrm{gender}}b_{\mathrm{age}}\sigma_{x_{\mathrm{gender}}, x_{\mathrm{age}}} + b_{A}\sigma_{\varepsilon_{A}}^2 \end{aligned} \right. \tag{7.17}\] となります。 これを 図 7.7 に照らし合わせると,例えば\(\sigma_{x_{A}}^2\)は
Q1_A→gender→Q1_A(\(b_{\mathrm{gender}}^2\sigma_{x_{\mathrm{gender}}}^2\))Q1_A→age→Q1_A(\(b_{\mathrm{age}}^2\sigma_{x_{\mathrm{age}}}^2\))Q1_A→gender→age→Q1_A(\(b_{\mathrm{gender}}b_{\mathrm{age}}\sigma_{x_{\mathrm{gender}}, x_{\mathrm{age}}}\))Q1_A→age→gender→Q1_A(\(b_{\mathrm{gender}}b_{\mathrm{age}}\sigma_{x_{\mathrm{gender}}, x_{\mathrm{age}}}\))Q1_A→e_A→Q1_A(\(\sigma_{\varepsilon_{A}}^2\))
の和になっています。検証的因子分析のときと同じように,自分自身を出発してから最低1つの外生変数を通過して戻るまでの全経路の係数の和になっているわけです。同様に,共分散\(\sigma_{x_{E}, x_{A}}\)では
Q1_E→Q1_A→gender→Q1_A(\(b_{A}b_{\mathrm{gender}}^2\sigma_{x_{\mathrm{gender}}}^2\))Q1_E→Q1_A→age→Q1_A(\(b_{A}b_{\mathrm{age}}^2\sigma_{x_{\mathrm{age}}}^2\))Q1_E→Q1_A→gender→age→Q1_A(\(b_{A}b_{\mathrm{gender}}b_{\mathrm{age}}\sigma_{x_{\mathrm{gender}}, x_{\mathrm{age}}}\))Q1_E→Q1_A→age→gender→Q1_A(\(b_{A}b_{\mathrm{gender}}b_{\mathrm{age}}\sigma_{x_{\mathrm{gender}}, x_{\mathrm{age}}}\))Q1_E→Q1_A→e_A→Q1_A(\(b_{A}\sigma_{\varepsilon_{A}}^2\))
という感じで,Q1_EからQ1_Aへの全経路での係数の和の形になっていると見ることができます8。
というわけで,モデル上の共分散行列\(\symbf{\Sigma}\)を求めることが出来ました。あとはこれに対応するデータ上の分散(4つ)と共分散(6つ)を用いて,5つのパラメータ\(\left(b_A, b_{\mathrm{age}},b_{\mathrm{gender}},\sigma_{\varepsilon_{A}}^2,\sigma_{\varepsilon_{E}}^2\right)\)を推定するだけです。
実際に計算してみると, \[ \left\{ \begin{aligned} \sigma_{x_{\mathrm{age}}}^2 &= 120.254 \\ \sigma_{x_{\mathrm{gender}}}^2 &= 0.221 \\ \sigma_{x_{\mathrm{gender}}, x_{\mathrm{age}}} &= 0.204 \\ b_A &= 0.550 \\ b_{\mathrm{age}} &= 0.071 \\ b_{\mathrm{gender}} &= 1.891 \\ \sigma_{\varepsilon_{A}}^2 &= 19.210 \\ \sigma_{\varepsilon_{E}}^2 &= 22.154 \end{aligned} \right. \] という解が得られます(上3つはデータから直接求めた値)。これを(7.17)式に当てはめてみると, \[ \begin{aligned} \symbf{\Sigma} &= \begin{bmatrix} \sigma_{x_{\mathrm{age}}}^2 & & & \\ \sigma_{x_{\mathrm{gender}}, x_{\mathrm{age}}} & \sigma_{x_{\mathrm{gender}}}^2 & & \\ \sigma_{x_{A}, x_{\mathrm{age}}} & \sigma_{x_{A}, x_{\mathrm{gender}}} & \sigma_{x_{A}}^2 & \\ \sigma_{x_{E}, x_{\mathrm{age}}} & \sigma_{x_{E}, x_{\mathrm{gender}}} & \sigma_{x_{E}, x_{A}} & \sigma_{x_{E}}^2 \end{bmatrix} = \begin{bmatrix} 120.254 & & & \\ 0.204 & 0.221 & & \\ 8.902 & 0.432 & 20.685 & \\ 4.892 & 0.238 & 11.354 & 28.395 \end{bmatrix} \end{aligned} \] となります。また,データ上の共分散行列の値は \[ \symbf{S} = \begin{bmatrix} 120.254 & & & \\ 0.204 & 0.221 & & \\ 8.906 & 0.433 & 20.667 & \\ 4.198 & 0.260 & 11.359 & 28.407 \end{bmatrix} \] となり,だいぶ近い値が得られました。
7.4 Rでやってみる(回帰分析・パス解析)
それでは,lavaanを使って回帰分析をやってみましょう。 sem()関数を使うと,回帰分析を含むパス解析に適した設定で自動的に推定を行ってくれます。
モデル構文では,lm()やglm()のときと同じように,両辺をチルダ(~)でつなげることで観測変数どうしの回帰を表します。 ということで,単回帰分析であれば以下のように1文だけのモデル構文を書けばよいわけです。
lavaan 0.6-20 ended normally after 1 iteration
Estimator ML
Optimization method NLMINB
Number of model parameters 2
Number of observations 2432
Model Test User Model:
Test statistic 0.000
Degrees of freedom 0
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Regressions:
Estimate Std.Err z-value P(>|z|)
Q1_A ~
age 0.074 0.008 8.952 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.Q1_A 19.999 0.574 34.871 0.000基本的な結果の見方は因子分析の時と同じです。 出力のRegressions:の部分が回帰係数を,Variances:の部分が誤差分散を表しています。 先程説明したように,SEMでは共分散構造のみを扱うならば,切片\(b_0\)は推定の対象にならないため,切片項\(b_0\)の推定値は出力されていません。 これを出すためには,モデル式に少し手を加える必要があります。 これもlm()やglm()の時と同じなのですが,回帰式に"+ 1"を加えると,切片項を明示的に推定するように指示することが出来ます。
lavaan 0.6-20 ended normally after 1 iteration
Estimator ML
Optimization method NLMINB
Number of model parameters 3
Number of observations 2432
Model Test User Model:
Test statistic 0.000
Degrees of freedom 0
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Regressions:
Estimate Std.Err z-value P(>|z|)
Q1_A ~
age 0.074 0.008 8.952 0.000
Intercepts:
Estimate Std.Err z-value P(>|z|)
.Q1_A 21.122 0.253 83.433 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.Q1_A 19.999 0.574 34.871 0.000出力を見ると,新たにIntercepts:という欄ができています。これが切片を表している部分です。 一応,ここまでの結果を,lm()で普通に回帰分析を行った場合と比較してみましょう。
Call:
lm(formula = model, data = dat)
Residuals:
Min 1Q Median 3Q Max
-18.565 -2.602 0.621 3.361 8.064
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 21.121738 0.253261 83.399 <2e-16 ***
age 0.074029 0.008273 8.949 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 4.474 on 2430 degrees of freedom
Multiple R-squared: 0.0319, Adjusted R-squared: 0.0315
F-statistic: 80.08 on 1 and 2430 DF, p-value: < 2.2e-16lm()では最小二乗法で解を求めている一方,lavaanはデフォルトでは最尤法で解を求めています。 推定法の違いはありますが,回帰係数および切片はほぼ一致する値が得られました。
続いてパス解析もやってみましょう。 基本的には一つ一つの回帰式を順番に書いていけば良いだけです。簡単ですね。
lavaan 0.6-20 ended normally after 1 iteration
Estimator ML
Optimization method NLMINB
Number of model parameters 5
Number of observations 2432
Model Test User Model:
Test statistic 0.709
Degrees of freedom 2
P-value (Chi-square) 0.702
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Regressions:
Estimate Std.Err z-value P(>|z|)
Q1_A ~
gender 1.891 0.189 9.996 0.000
age 0.071 0.008 8.733 0.000
Q1_E ~
Q1_A 0.550 0.021 26.173 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.Q1_A 19.210 0.551 34.871 0.000
.Q1_E 22.154 0.635 34.871 0.0007.5 回帰分析と因子分析を組み合わせる
図 7.6 に基づくパス解析では,因子Aと因子Eに関する変数として和得点(Q1_AとQ1_E)を使用しました。 ですが和得点には独自因子(構成概念からすると誤差)の影響が残っているため,可能であれば因子得点を用いた方が「純粋」な構成概念得点であると考えられます。 あるいは(構成概念)妥当性の考え方の根底にあった「観測得点はあくまでも構成概念の顕在化」という考えに従えば,仮説モデルでは構成概念そのもの同士の関係(法則定立ネットワーク)を見るべきだと言えるでしょう。
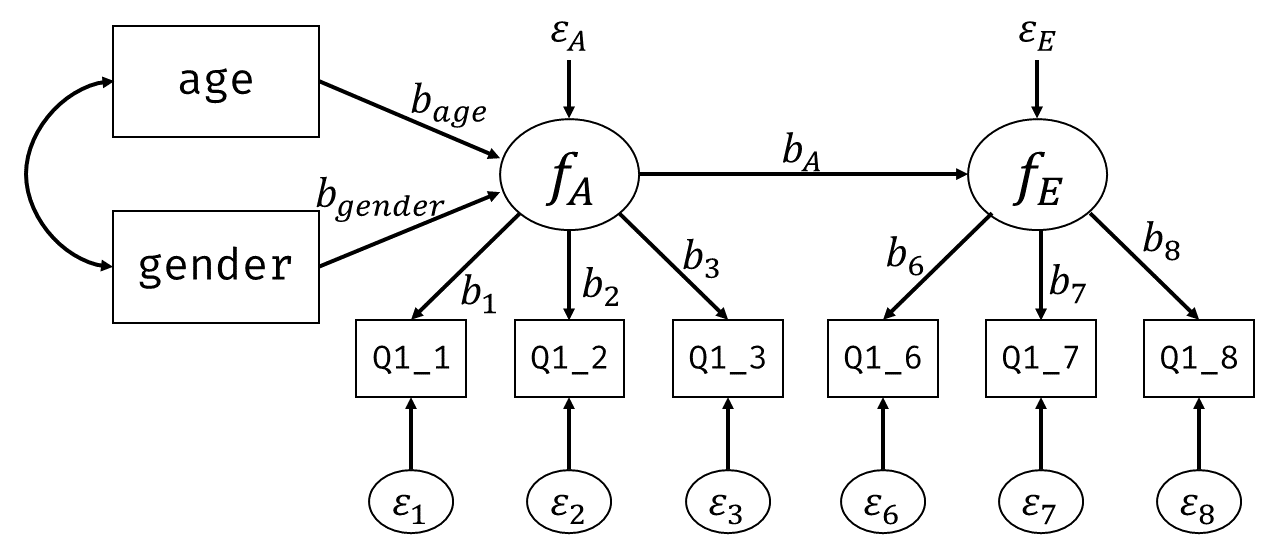
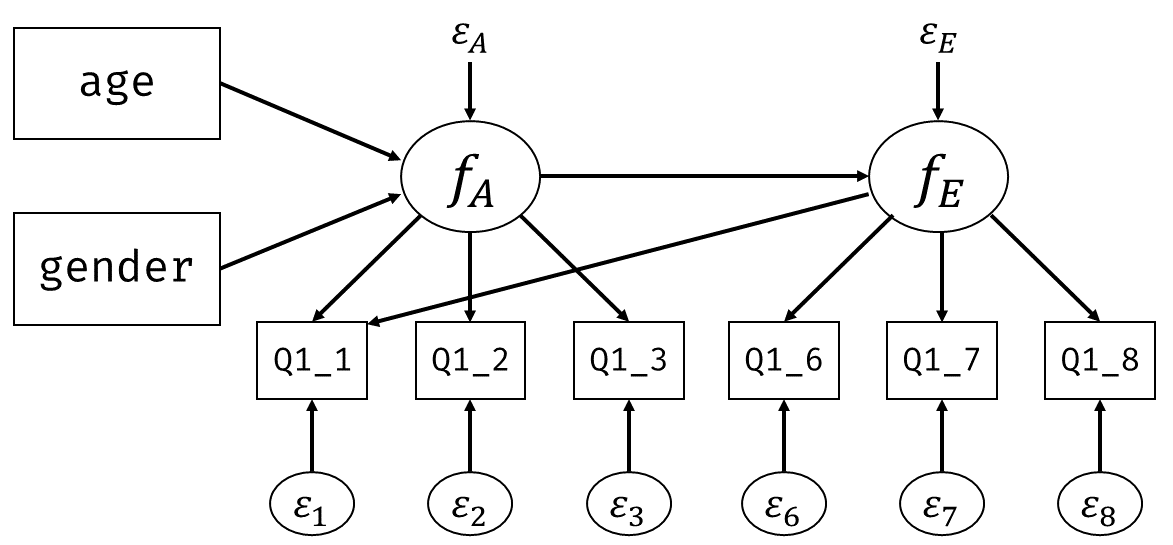
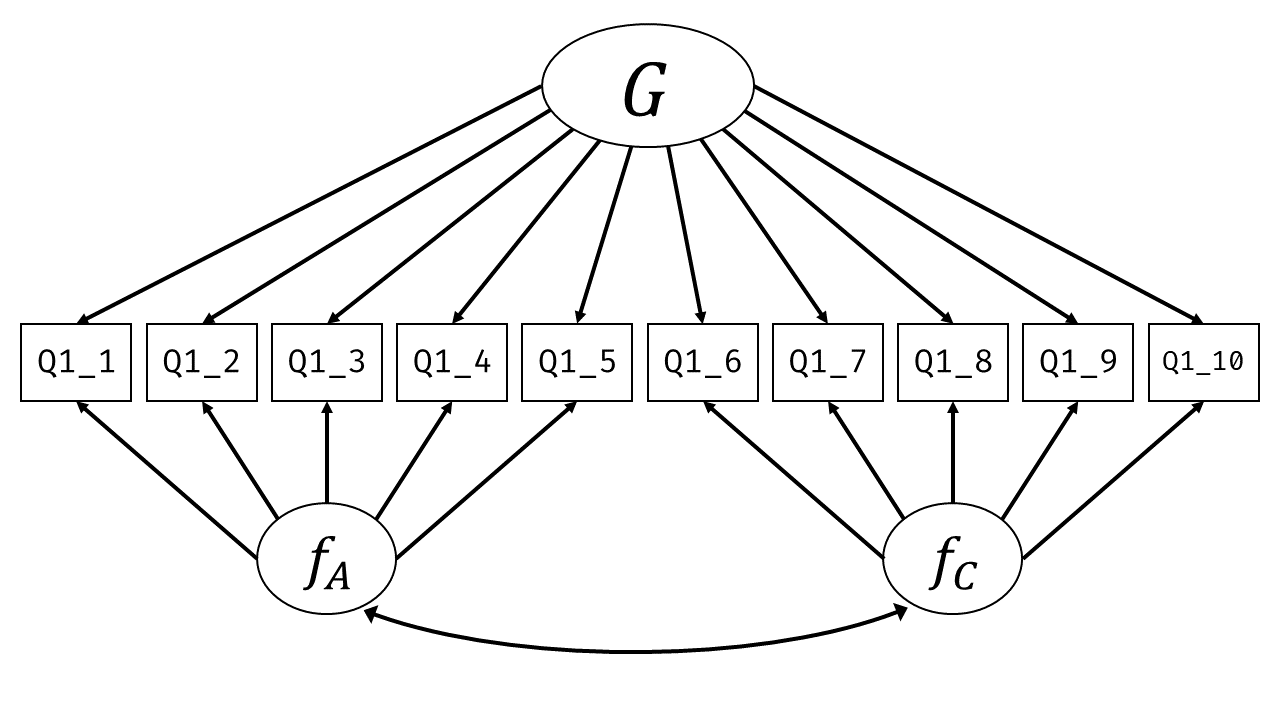
いま,手元には構成概念(因子)を構成する各項目の回答そのものがあります。 そこで, 図 7.3 の因子分析と 図 7.6 の回帰分析を組み合わせて, 図 7.8 のようなモデルを考えてみましょう。
モデルが複雑になってもやることは同じです。 全ての(標準化された)観測変数間の相関行列 \[ \symbf{\Sigma} = \begin{bmatrix} 1 & & & & & & & \\ r_{\mathrm{gender},\mathrm{age}} & 1 & & & & & \\ r_{y1,\mathrm{age}} & r_{y1,\mathrm{gender}} & 1 & & & & \\ r_{y2,\mathrm{age}} & r_{y2,\mathrm{gender}} & r_{y2, y1} & 1 & & \\ r_{y3,\mathrm{age}} & r_{y3,\mathrm{gender}} & r_{y3, y1} & r_{y3,y2} & 1 & \\ r_{y6,\mathrm{age}} & r_{y6,\mathrm{gender}} & r_{y6, y1} & r_{y6,y2} & r_{y6,y3} & 1 & & \\ r_{y7,\mathrm{age}} & r_{y7,\mathrm{gender}} & r_{y7, y1} & r_{y7,y2} & r_{y7,y3} & r_{y7,y6} & 1 & \\ r_{y8,\mathrm{age}} & r_{y8,\mathrm{gender}} & r_{y8, y1} & r_{y8,y2} & r_{y8,y3} & r_{y8,y6} & r_{y8,y7} & 1 \\ \end{bmatrix} \] と,データ上の相関行列 \[ \symbf{S} = \begin{bmatrix} 1 & & & & & & & \\ 0.039 & 1 & & & & & \\ 0.156 & 0.157 & 1 & & & & \\ 0.113 & 0.184 & 0.353 & 1 & & \\ 0.064 & 0.137 & 0.274 & 0.497 & 1 & \\ 0.095 & 0.008 & -0.011 & 0.098 & 0.110 & 1 & & \\ 0.018 & 0.060 & -0.011 & 0.124 & 0.142 & 0.435 & 1 & \\ 0.065 & 0.048 & 0.024 & 0.185 & 0.126 & 0.313 & 0.359 & 1 \\ \end{bmatrix} \] がなるべく近くなるように各種パラメータを推定してあげます。
ここでいくつかの変数間のモデル上の相関係数を具体的に見てみましょう。 同じ因子に属するQ1_1とQ1_2の相関は,(検証的)因子分析のときには2項目の因子負荷の積\((b_{11}b_{21})\)という簡単な形で表すことができていました。 今回のモデルではどうでしょうか。 因子得点は内生変数として扱われており,\(f_A=b_{\mathrm{age}}x_{\mathrm{age}}+b_{\mathrm{gender}}x_{\mathrm{gender}}+\varepsilon_{A}\)という回帰式になっています。 これまでと同じようにQ1_1とQ1_2をそれぞれ外生変数(ageとgender)の関数になるまで展開してあげるならば, \[
\begin{split}
y_1 &= f_Ab_{1} + \varepsilon_{1}\\
&= (b_{\mathrm{age}}x_{\mathrm{age}}+b_{\mathrm{gender}}x_{\mathrm{gender}}+\varepsilon_{A})b_{1} + \varepsilon_{1}\\
y_2 &= f_Ab_{2} + \varepsilon_{2}\\
&= (b_{\mathrm{age}}x_{\mathrm{age}}+b_{\mathrm{gender}}x_{\mathrm{gender}}+\varepsilon_{A})b_{2} + \varepsilon_{2}
\end{split}
\tag{7.18}\] となり,これを頑張って展開して相関を求める必要がありそうです。 しかしよく考えてみると,因子分析モデルでは潜在変数の分散を1に固定する,という制約がありました。 つまり\(f_A=(b_{\mathrm{age}}x_{\mathrm{age}}+b_{\mathrm{gender}}x_{\mathrm{gender}}+\varepsilon_{A})\)の部分は,これをすべて合わせて分散1になるように調整されるということです。 したがってこの2項目の相関を求めると,結局 セクション 6.4.1 の議論 に帰着して9 \[
\begin{split}
r_{y1,y2} &= r_{(f_Ab_{1}+ \varepsilon_{1}), (f_Ab_{2}+ \varepsilon_{2})} \\
&= r_{(f_Ab_{1}),(f_Ab_{2})} \\
&= b_{1}b_{2}\left(\sigma_{f_A}\right) \\
&= b_{1}b_{2}
\end{split}
\tag{7.19}\] となるのです。 また,誤差分散\(\sigma_{\varepsilon_{A}}^2\)の値は1から回帰係数の二乗和をひいた値になっています。 このあたりの議論は,矢印の向きこそ反対ですが因子分析の時に見た「観測変数の分散は因子負荷の二乗和と独自因子の分散の和になっている」というのと同じですね。
続いて最も距離の遠いageとQ1_8の相関を見てみます。 Q1_8を外生変数(ageとgender)の関数に戻してあげると, \[
\begin{split}
y_8 &= f_Eb_{8} + \varepsilon_{8}\\
&= (b_{A}f_{A}+\varepsilon_{E})b_{8} + \varepsilon_{8}\\
&= \left(b_{A}\left[b_{\mathrm{age}}x_{\mathrm{age}}+b_{\mathrm{gender}}x_{\mathrm{gender}}+\varepsilon_{A}\right]+\varepsilon_{E}\right)b_{8} + \varepsilon_{8} \\
&= b_{A}b_{8}\left(b_{\mathrm{age}}x_{\mathrm{age}}+b_{\mathrm{gender}}x_{\mathrm{gender}}\right) + \overbrace{b_Ab_8\varepsilon_{A} + b_8\varepsilon_{E} + \varepsilon_{8}}^{\mathrm{error}}
\end{split}
\tag{7.20}\] となります。後ろの\(\varepsilon\)に関する項(\(\mathrm{error}\))は,観測変数ageとの相関はゼロなはずなので無視して分散を求めると, \[
\begin{split}
r_{\mathrm{age}, y8} &= b_Ab_8b_{\mathrm{age}}\sigma_{\mathrm{age}}^2 + b_Ab_8b_{\mathrm{gender}}\sigma_{\mathrm{age},\mathrm{gender}} \\
&= b_Ab_8b_{\mathrm{age}} + b_Ab_8b_{\mathrm{gender}}\sigma_{\mathrm{age},\mathrm{gender}}
\end{split}
\tag{7.21}\] となります。ここでもやはり
Q1_8→f_E→f_A→age(\(b_Ab_8b_{\mathrm{age}}\))Q1_8→f_E→f_A→gender→age(\(b_Ab_8b_{\mathrm{gender}}\sigma_{\mathrm{age},\mathrm{gender}}\))
という要領で,2変数間の全経路の係数の積の和の形になっていることがわかります。
モデルが複雑になっても,内部でやっていることは今までと同じであることを確認したので,実際にRで推定を行ってみましょう。
6行目(age ~~ gender)は,ageとgenderの共分散を明示的に推定するように指示しています(任意)。 書かなくても勝手にデータから計算した値を使ってくれるので,この行の有無でパラメータの推定値が変わることはないのですが,この行を書くことによって,結果の出力にデータの共分散の値を表示してくれるようになります。
lavaan 0.6-20 ended normally after 36 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 18
Number of observations 2432
Model Test User Model:
Test statistic 129.227
Degrees of freedom 18
P-value (Chi-square) 0.000
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_A =~
Q1_1 0.602 0.031 19.255 0.000 0.628 0.447
Q1_2 0.888 0.030 29.426 0.000 0.926 0.790
Q1_3 0.786 0.030 25.796 0.000 0.819 0.627
f_E =~
Q1_6 0.728 0.031 23.767 0.000 0.753 0.611
Q1_7 0.888 0.035 25.607 0.000 0.918 0.698
Q1_8 0.651 0.031 21.262 0.000 0.673 0.523
Regressions:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_A ~
age 0.014 0.002 6.275 0.000 0.013 0.147
gender 0.522 0.053 9.894 0.000 0.501 0.236
f_E ~
f_A 0.252 0.030 8.402 0.000 0.254 0.254
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
age ~~
gender 0.204 0.105 1.945 0.052 0.204 0.039
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Q1_1 1.581 0.051 31.144 0.000 1.581 0.801
.Q1_2 0.517 0.046 11.273 0.000 0.517 0.376
.Q1_3 1.034 0.046 22.666 0.000 1.034 0.607
.Q1_6 0.950 0.043 22.240 0.000 0.950 0.626
.Q1_7 0.889 0.055 16.228 0.000 0.889 0.513
.Q1_8 1.205 0.044 27.533 0.000 1.205 0.727
age 120.254 3.449 34.871 0.000 120.254 1.000
gender 0.221 0.006 34.871 0.000 0.221 1.000
.f_A 1.000 0.920 0.920
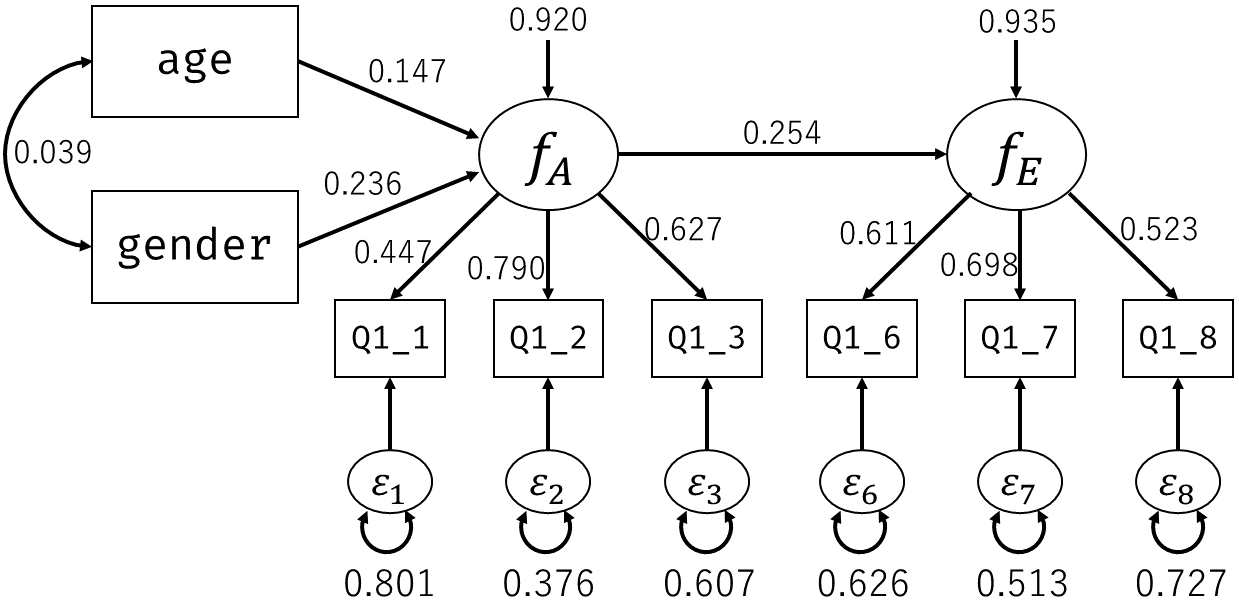
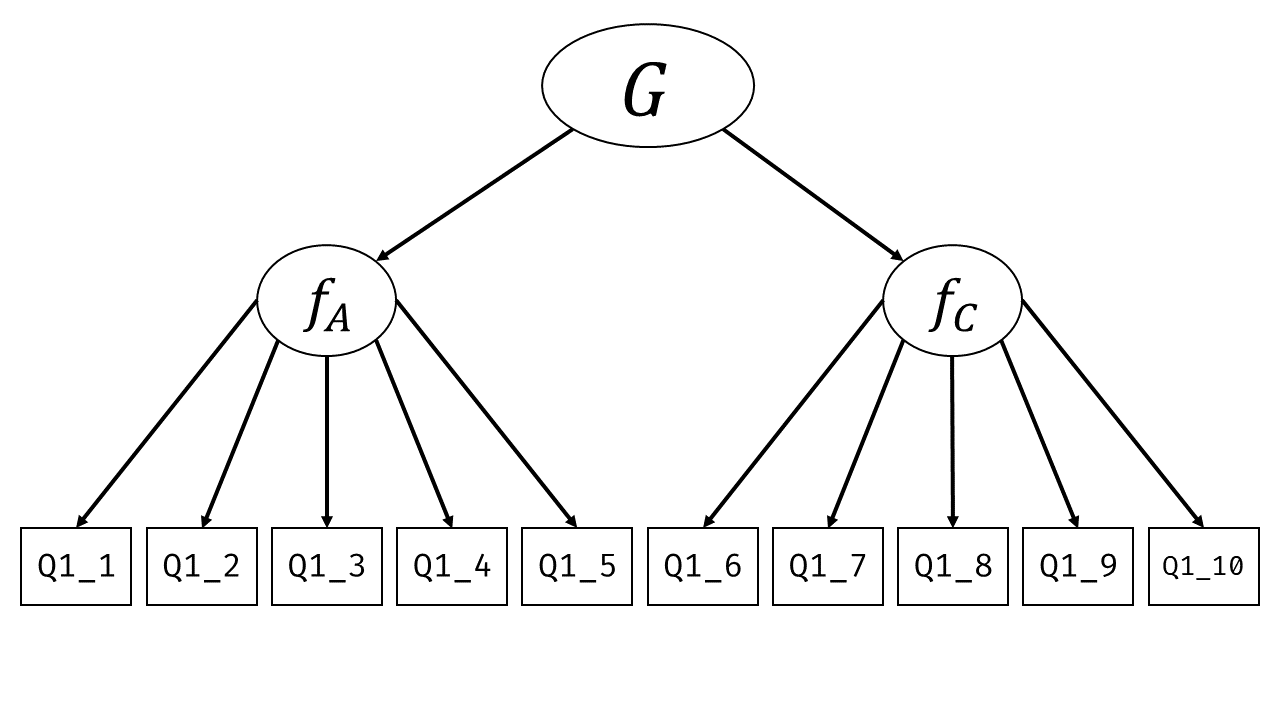
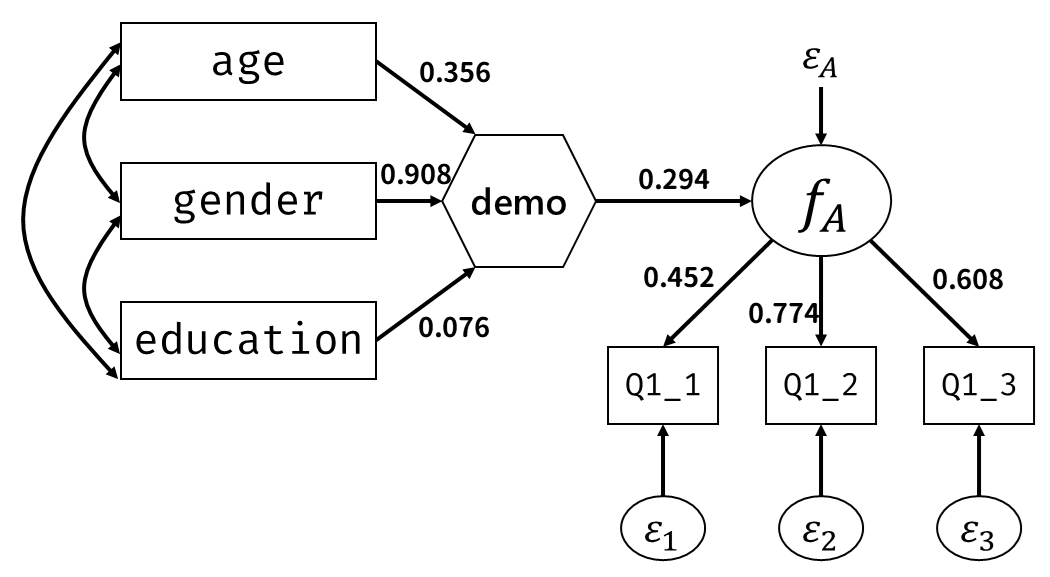
.f_E 1.000 0.935 0.935結果の見方も同じなので省略します。一応全ての標準化解を 図 7.8 に書き加えると, 図 7.9 のようになるわけです。 実際に論文などで報告する際には,全ての値を載せるとごちゃごちゃしてしまう可能性があります。 そこで,以下のような省略を行い簡潔化することがあります。 このあたりは自由というか,どういう基準で簡略化したかがハッキリわかればOKです。
- 因子分析の部分は書かない(因子だけ残す)
- 係数が一定以下のところには矢印をひかない
- 統計的に有意ではない係数のところは矢印をひかない
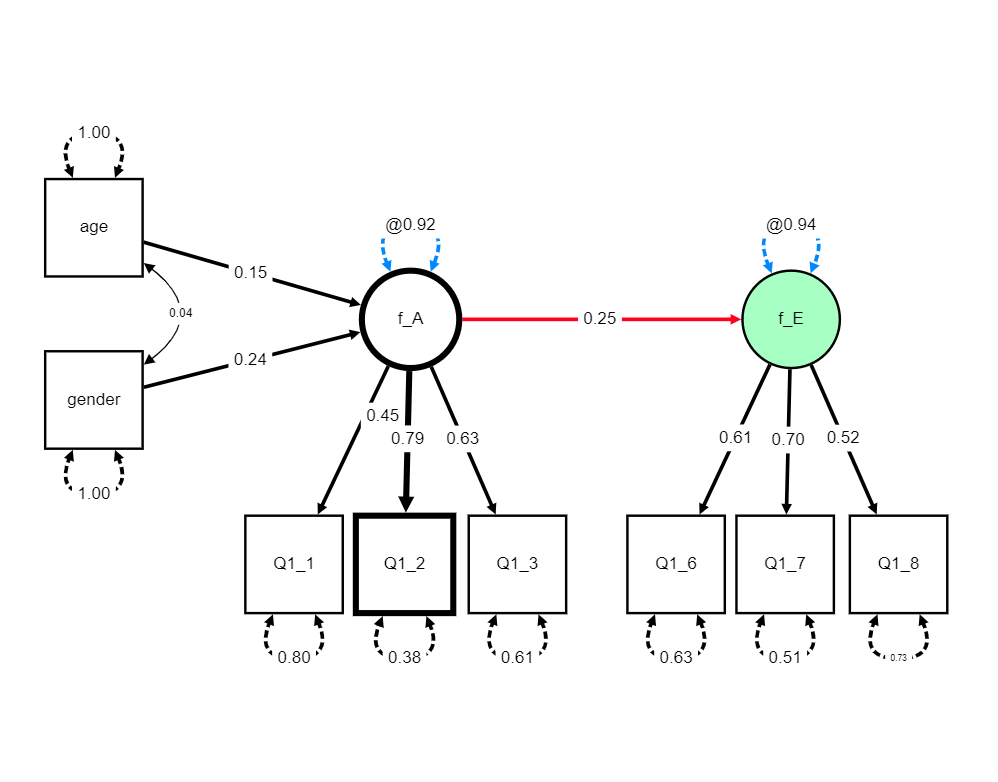
lavaanの関数(cfa()やsem())によって得られた結果のオブジェクトから,自動的にパス図を作ってくれるものとして,lavaanPlotパッケージというものが用意されています。 こういったものを利用して,自分で書いたモデルのコードが正しいものだったかをきちんと確認しておくと良いでしょう。 lavaanPlotパッケージは, 図 7.10 のように比較的そのまま論文にも載せられそうなレベルのきれいな図を書いてくれます。 ただ,見た目の点では変数名を変えたり,微妙に矢印の位置を調整したりする必要が出てくることが多いと思うので,最終的にはPowerPointやIllustratorなどを使って自分で図を作ったほうが良さそうです。
lavaanguiパッケージ
2024年9月に新しくCRANにリリースされたlavaanguiパッケージは,その名の通りGUIで操作可能な形でlavaanを利用できるパッケージです。 基本的な機能は2種類で,まず1つ目はGUIでモデル式を自動作成できる機能です。 使い方は簡単で,lavaangui()を実行するとウェブブラウザ上にGUIの画面が表示されます10。 後はマルや四角や矢印を適宜置いていくだけです。 この講義資料の上ではそこまで表示できないので,ぜひ手元で試してみてください。
2つ目の機能は,cfa()やsem()関数で推定した結果を図示する機能です。 lavaanguiパッケージの強みは,表示された図をグリグリ動かせる点です。 つまり,各変数の位置をうまく調整することで,そのまま論文に載せられるレベルの図が作れるかもしれません。
実際に弄ってみると分かりますが,各要素の色やフォントサイズなどは一つ一つ自由に変更可能です。 また,いろいろと弄った後のものをFile > Download modelで保存可能なので,あとで編集を再開するといったことも可能です。
semPlotパッケージもあるよ
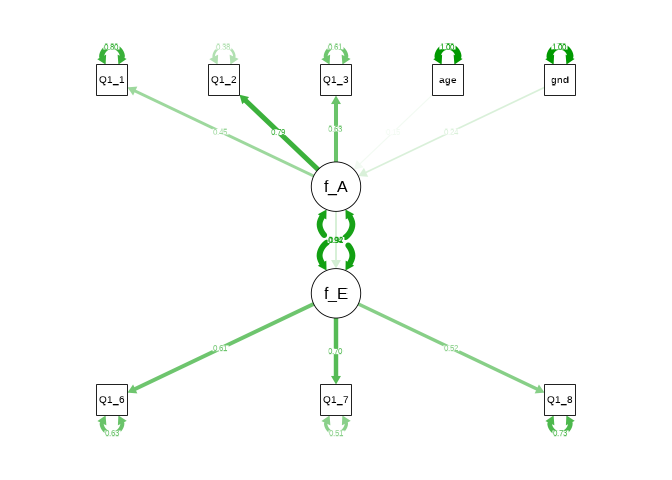
結果のオブジェクトから自動的にパス図を作成してくれるものとしては,semPlotパッケージにあるsemPaths()という関数もあります。 lavaanPlotと比べても,残念ながらそのまま論文に載せられるほど高性能ではないのですが,自分の書いたモデル式に間違いが無いかを確認したり,係数が一定以下のところを除外したときの図をさっと確認するのには使えると思います。
(lavaanPlotは比較的新しいパッケージでまだ挙動の変更の可能性があるので,なんかうまくいかない場合のプランBとして補足的に紹介しておきます。)
7.5.1 (おまけ)SEMモデルを一つの式で表す
ここまでに見てきたように,SEMは回帰分析と因子分析を内包する上位の概念です。 回帰分析も因子分析も,「被説明変数を説明変数の線形和で表現する」という点は変わらないので,これらがくっついたモデル( 図 7.8 )であっても,これまでと同じように線形代数を使えば一つの式で表すことができます(Adachi, 2020)。
まず,因子分析の部分(潜在変数から観測変数に矢印が引かれている部分)だけ見てみると,これは単純な2因子モデルなので, \[ \symbf{y}_p = \symbf{f}_p\symbf{B}^{(1)} + \symbf{\varepsilon}_p^{(1)} \tag{7.22}\] と表すことができます。上付きの添字\((1)\)は,因子分析パートと回帰分析パートの\(\symbf{B}\)や\(\symbf{\varepsilon}\)を区別するために便宜的につけているものです。 それぞれを展開すると, \[ \begin{split} \begin{bmatrix} y_{p1} & y_{p2} & y_{p3} & y_{p6} & y_{p7} & y_{p8} \end{bmatrix} = & \begin{bmatrix} f_{p\mathrm{A}} & f_{p\mathrm{E}} \end{bmatrix} \begin{bmatrix} b_{11} & b_{21} & b_{31} & 0 & 0 & 0 \\ 0 & 0 & 0 & b_{62} & b_{72} & b_{82} \end{bmatrix} \\ & + \begin{bmatrix} \varepsilon_{p1} & \varepsilon_{p2} & \varepsilon_{p3} & \varepsilon_{p6} & \varepsilon_{p7} & \varepsilon_{p8} \end{bmatrix} \end{split} \tag{7.23}\] となります。 同様に,回帰分析の部分は, \[ f_{p\mathrm{E}} = f_{p\mathrm{A}}b_{\mathrm{A}} + \symbf{\varepsilon}_p^{(2)} \tag{7.24}\] となります。 ここで,因子分析の表現に合わせるため,式の左辺にすべての潜在変数が登場するように少し式を書き換えます。具体的には \[ \left\{ \begin{alignedat}{2} f_{p\mathrm{A}} &= & & f_{p\mathrm{A}} \\ f_{p\mathrm{E}} &= f_{p\mathrm{A}}b_{\mathrm{A}} & + & \varepsilon_{p\mathrm{A}} \end{alignedat} \right. \tag{7.25}\] という連立方程式を用意し,これを行列によって \[ \begin{aligned} \begin{bmatrix} f_{p\mathrm{A}} & f_{p\mathrm{E}} \end{bmatrix} &= \begin{bmatrix} f_{p\mathrm{A}} & f_{p\mathrm{E}} \end{bmatrix} \begin{bmatrix} 0 & b_{\mathrm{A}} \\ 0 & 0 \end{bmatrix} + \begin{bmatrix} f_{p\mathrm{A}} & \varepsilon_{p\mathrm{A}} \end{bmatrix} \\ \longrightarrow \symbf{f}_p &= \symbf{f}_p\symbf{B}^{(2)} + \symbf{\varepsilon}_p^{(2)} \end{aligned} \tag{7.26}\] と表現します。
これで準備は完了です。あとは(7.23)式と(7.26)式をうまく組み合わせると, \[ \begin{aligned} \begin{bmatrix} \symbf{f}_p & \symbf{y}_p \end{bmatrix} &= \begin{bmatrix} \symbf{f}_p & \symbf{y}_p \end{bmatrix} \begin{bmatrix} \symbf{B}^{(1)} & \symbf{B}^{(2)} \\ \symbf{0} & \symbf{0} \end{bmatrix} + \begin{bmatrix} \symbf{\varepsilon}_p^{(1)} & \symbf{\varepsilon}_p^{(2)} \end{bmatrix} \\ \longrightarrow \symbf{v}_p &= \symbf{v}_p\symbf{B} + \symbf{\varepsilon}_p \end{aligned} \tag{7.27}\] となります。 回帰係数行列の\(\symbf{0}\)は,今回のモデルでは\(y\)から\(f\)への回帰や\(y\)同士の回帰は一つも無いため,ゼロ行列を置いています。 もしも\(y\)同士の回帰などがあれば,それに応じて係数を入れる必要があります。 とにかく,これによってすべての(観測・潜在)変数同士の回帰分析のモデルを統一的に表すことができました。
ちなみに展開すると横長になりすぎてかなり見にくいですが,一応 \[ \begin{aligned} \begin{split} & \begin{bmatrix} f_{p\mathrm{A}} & f_{p\mathrm{E}} & y_{p1} & y_{p2} & y_{p3} & y_{p6} & y_{p7} & y_{p8} \end{bmatrix} = \\ & \begin{bmatrix} f_{p\mathrm{A}} & f_{p\mathrm{E}} & y_{p1} & y_{p2} & y_{p3} & y_{p6} & y_{p7} & y_{p8} \end{bmatrix} \begin{bmatrix} 0 & b_{\mathrm{A}} & b_{11} & b_{21} & b_{31} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & b_{62} & b_{72} & b_{82} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix} \\ & + \begin{bmatrix} f_{p\mathrm{A}} & \varepsilon_{p\mathrm{A}} & \varepsilon_{p1} & \varepsilon_{p2} & \varepsilon_{p3} & \varepsilon_{p6} & \varepsilon_{p7} & \varepsilon_{p8} \end{bmatrix} \end{split} \end{aligned} \tag{7.28}\] という形をしています。
あとは(7.27)式を,左辺が\(\symbf{y}\)のみになるように変形していくだけです。 \((T+I)\)単位行列\(\symbf{I}_{(T+I)}\)を用いると \[ \symbf{v}_p\symbf{I}_{(T+I)} = \symbf{v}_p\symbf{B} + \symbf{\varepsilon}_p \tag{7.29}\] と表せるので,\(\symbf{v}_p\symbf{B}\)を移項させてから両辺に逆行列をかけると \[ \symbf{v}_p = \symbf{\varepsilon}_p(\symbf{I}_{(T+I)}-\symbf{B})^{-1} \tag{7.30}\] と変形させることができます。 ここで, \[ \begin{aligned} \symbf{v}_p = \begin{bmatrix} \symbf{f}_p & \symbf{y}_p \end{bmatrix} \end{aligned} \tag{7.31}\] であることを踏まえると,\(\symbf{v}_p\)のうち\(\symbf{f}_p\)に当たる部分が0になったものが\(\symbf{y}_p\)なので,\((T\times T)\)のゼロ行列\(\symbf{0}_{(T)}\)と,\((I\times I)\)の単位行列\(\symbf{I}_{(I)}\)を縦に並べた行列\(\symbf{H}\)を使って, \[ \begin{aligned} \begin{split} \symbf{y}_p &= \begin{bmatrix} \symbf{f}_p & \symbf{y}_p \end{bmatrix}\begin{bmatrix} \symbf{0}_{(T)} \\ \symbf{I}_{(I)} \end{bmatrix} \\ &= \symbf{v}_p\symbf{H} \end{split} \end{aligned} \tag{7.32}\] と表せます。 あとは,これに(7.30)式を代入することで, \[ \symbf{y}_p = \symbf{\varepsilon}_p(\symbf{I}_{(T+I)}-\symbf{B})^{-1}\symbf{H} \tag{7.33}\] という形で,どんなSEMモデルであっても,すべての観測変数をすべてのパラメータの関数で表す一般化が完成しました。
7.6 モデルの適合度
ここまで,いくつかの簡単なモデルでSEMの基本的な仕組みを紹介しました。 SEMの目的はなるべく少ないモデルパラメータによってデータの共分散行列に近い値を再現することです。 データ(の共分散行列\(\symbf{S}\))に対するモデル(の共分散行列\(\symbf{\Sigma}\))の当てはまりの程度を表す指標を(モデルの)適合度と呼び,その指標には様々な種類があります。 以下でいくつかの代表的な指標を紹介します。 これらは,どれか一つ・一種類の指標を使えばOKというものではありません。 様々な視点からの評価を行い,総合的にモデルの適合度を判定するようにしましょう。 適合度指標に関する議論は,星野 他 (2005) あたりが詳しいです。
7.6.1 相対的指標
相対的指標では,「最悪のモデル」と比べてどの程度当てはまりが改善したかを考えます。 ここでの「最悪のモデル」とは,全ての変数が完全に無相関だと仮定したモデルです。 例えば 図 7.6 のパス解析で考えると,このモデルには計4個の観測変数が登場するので,「最悪のモデル」は 図 7.11 のような状態です。
何もないということは,モデル上の相関行列\(\symbf{\Sigma}_0\)は \[ \symbf{\Sigma}_0 = \begin{bmatrix} \sigma_{x_{\mathrm{age}}}^2 & & & \\ 0 & \sigma_{x_{\mathrm{gender}}}^2 & & \\ 0 & 0 & \sigma_{x_{A}}^2 & \\ 0 & 0 & 0 & \sigma_{x_{E}}^2 \end{bmatrix} \tag{7.34}\]
ということです。もちろんこれ以上当てはまりの悪いモデルは考えられません。 ということで,相対的指標ではこの独立モデル(ヌルモデル)と比べて,設定したモデルではどの程度当てはまりが改善したかを確認します11。 ここで用いる「当てはまり」の指標は,最尤推定の場合は尤度を元に設定します。 分析者が設定した仮説モデルに関する当てはまりの指標\(L_{h}\)は \[ L_{h} = (P-1)\left\{\mathrm{tr}(\symbf{\Sigma}^{-1}\symbf{S}) - \log\vert\symbf{\Sigma}^{-1}\symbf{S}\vert - I\right\} \tag{7.35}\] となります。この式は,最尤推定量におけるモデルの尤度(波括弧の中身)を\(P-1\)倍したものなのですが,細かい式の意味や導出はともかく,この値が「データにおける観測された共分散行列\(\symbf{S}\)」と「仮説モデルの共分散行列\(\symbf{\Sigma}\)」の比(\(\symbf{\Sigma}^{-1}\symbf{S}\))に基づく値だということだけ理解しておいてください。 つまりこの値は\(\symbf{\Sigma}\)と\(\symbf{S}\)の値が近くなるほど小さな値を取る,いわば乖離度のようなものを表しています12。 そして同様に,独立モデルでの当てはまりの指標\(L_{0}\)を \[ L_{0} = (P-1)\left\{\mathrm{tr}(\symbf{\Sigma}_0^{-1}\symbf{S}) - \log\vert\symbf{\Sigma}_0^{-1}\symbf{S}\vert - I\right\} \tag{7.36}\] とします。 相対的指標では,この\(L_{h}\)と\(L_{0}\)を比較していきます。
相対的指標でよく用いられている指標の一つは,TLI (Tucker-Lewis index: Tucker & Lewis, 1973) でしょう。 \[ \mathrm{TLI} = \frac{\frac{L_{0}}{df_{0}}-\frac{L_{h}}{df_{h}}}{\frac{L_{0}}{df_{0}}-1} \tag{7.37}\] \(df_{h}\)と\(df_{0}\)はそれぞれ仮説モデルと独立モデルでの自由度です。自由度はデータの分散共分散の総数(\(\frac{I(I+1)}{2}\))からパラメータ数を引いた数になります。 例えば 図 7.6 のモデルでは,4つの観測変数から計算できる分散(\(4\)個)と共分散(\({}_4\mathrm{C}_2=6\)個)の総数10個を8つのモデルパラメータで表現しました。そのため自由度は\(df_{h}=2\)となります。 本来データの分散共分散は10個あったのに,8個だけでそれを再現したという意味では,自由度は「何個のパラメータを削減しているか」という見方もできそうです。
あらためてTLIの式を見てみます。 \(\frac{L_{0}}{df_{0}}\)は独立モデルでの乖離度です。削減したパラメータ1個につきどの程度のズレが発生したかを表しています13。 これに対して,\(\frac{L_{h}}{df_{h}}\)は仮説モデルでの乖離度です。 あってもなくても良いパラメータは削減しても大きなズレは発生しないですが,重要なパラメータを削減すると大きなズレが発生します。 ズレの大きさをパラメータ数で割ることで,「(ヌルモデルから)追加したパラメータ数の割に当てはまりが改善したか」を評価しているわけですね。
似たような指標に CFI (Comparative fit index: Bentler, 1990)があり,これもよく用いられています。 \[ \mathrm{CFI} = 1-\frac{\max(L_{h}-df_{h},0)}{\max(L_{h}-df_h,L_0-df_0,0)} \tag{7.38}\] CFIでは乖離度\(L_h\)から自由度\(df_h\)を引いています。 が,あとは大体同じです。分母の方の\(\max\)関数では,普通は最も乖離度の大きい\(L_0-df_0\)が選ばれるはずです。 そうなると \[ \mathrm{CFI}= 1- \frac{L_{h}-df_{h}}{L_0-df_0} \tag{7.39}\] となり,仮説モデルにおける当てはまりの改善度を表していることがよくわかります。
TLIやCFIは1に近いほど良い指標です。一般的には0.9くらいはほしいだの0.95あると嬉しいだの言われています。 しかし\(L_h\)は\(\symbf{\Sigma}\)と\(\symbf{S}\)のズレの大きさに規定されている以上,基本的にはパラメータ数を増やすほど値が改善していくという点には注意が必要です。
7.6.2 絶対的指標
データの相関行列\(\symbf{S}\)とモデルの相関行列\(\symbf{\Sigma}\)の要素レベルでのズレを \[ \symbf{E} = \symbf{\Sigma} - \symbf{S} \tag{7.40}\] と表すと,適合度の指標として\(\symbf{E}\)の部分がどれだけ小さいかという発想が自然に出てきます。 例えば 図 7.6 のパス解析では, \[ \begin{aligned} \symbf{E} &= \symbf{\Sigma} - \symbf{S} \\ &= \begin{bmatrix} 120.254 & & & \\ 0.204 & 0.221 & & \\ 8.902 & 0.432 & 20.685 & \\ 4.892 & 0.238 & 11.354 & 28.395 \end{bmatrix} - \begin{bmatrix} 120.254 & & & \\ 0.204 & 0.221 & & \\ 8.906 & 0.433 & 20.667 & \\ 4.198 & 0.260 & 11.359 & 28.407 \end{bmatrix} \\ &= \begin{bmatrix} 0 & & & \\ 0 & 0 & & \\ -0.004 & -0.001 & 0.018 & \\ 0.694 & -0.022 & -0.005 & -0.012 \end{bmatrix} \end{aligned} \] という関係になっています。 ここから適合度を単純に考えると,例えば\(\symbf{E}\)の成分の平均のようなものを計算すると良さそうです。 この指標を RMR (root mean-squared residual) と呼び,式としては \[ \mathrm{RMR} = \sqrt{\frac{2}{I(I-1)}\sum_{i=1}^{I}\sum_{j=1}^{I}(\sigma_{ij}-s_{ij})^2} \tag{7.41}\] と表されます。ここで\(\sigma_{ij}, s_{ij}\)はそれぞれ\(\symbf{\Sigma}, \symbf{S}\)の\((i,j)\)成分の値を意味しています。 しかし,RMRは変数のスケールの影響を受けてしまいます。 例えば全ての変数の値を10倍(=分散は100倍)にしたとしたら,\(\symbf{S}\)と\(\symbf{\Sigma}\)の各要素の値は単純に100倍されてしまうため,\(\symbf{E}\)の平均であるRMRも100倍になってしまいます。
これでは基準を決められないので,RMRを標準化することで生まれたのが SRMR (standardized RMR: Hu & Bentler, 1999)です。 標準化の仕方は,「共分散から相関係数を導出する時」と同様にすることで, \[ \mathrm{SRMR} = \sqrt{\frac{2}{I(I-1)}\sum_{i=1}^{I}\sum_{j=1}^{I}\left(\frac{\sigma_{ij}-s_{ij}}{s_{ii}s_{jj}}\right)^2} \tag{7.42}\] と定式化されます。
SRMRの他にもよく使われる指標としては,GFI (Goodness of fit index: Bentler, 1983)があります。これも基本的な考え方は同じで,\(\symbf{S}\)と\(\symbf{\Sigma}\)の各要素の値が近いほど良くなります。 \[ \begin{aligned} \mathrm{GFI} &= 1-\frac{tr\left[\left(\symbf{S}-\symbf{\Sigma}\right)^2\right]}{tr[\symbf{S}^2]} \\ &= 1-\frac{\sum_{i=1}^{I}\sum_{j=1}^{i}(s_{ij}-\sigma_{ij})^2}{\sum_{i=1}^{I}\sum_{j=1}^{i}s_{ij}^2} \end{aligned} \tag{7.43}\]
SRMRやGFIは,回帰分析の決定係数や因子分析の分散説明率のようなもので,パラメータの数が多いほど値は改善していきます。 因子分析の分散説明率では「最低限これくらいは欲しい」といった考え方を紹介しました。 その観点ではこれらの指標は役に立ちます。 例えばSRMRでは0.08や0.05以下くらいだと良いと言われていたり,GFIや後述するAGFIは0.95以上だと良いと言われていたりします(Hancock et al., 2019; 豊田,2014)。 ですがSEMの目的は「なるべく少ないパラメータで」達成したいところです。 そう考えると,これらの指標だけを用いていると少し問題があるわけです。
ちなみに,GFIには自由度で調整したAGFI(Adjusted GFI)というものがあります。 \[ \mathrm{AGFI} = 1-\frac{I(I+1)}{2}\frac{1}{df}(1-\mathrm{GFI}) \tag{7.44}\] これは,自由度調整済み決定係数のような感じで,推定するパラメータ数が多くなるほど相関行列の乖離度\((1-\mathrm{GFI})\)を過大評価するような調整がされているわけです。
7.6.3 倹約的指標
データへの当てはまりは良いほど嬉しいのですが,「なるべく少ないパラメータで」を満たすために,先ほど紹介したAGFIのように推定するパラメータ数を考慮した適合度指標を考えます。 このクラスで多分最もよく用いられているのが RMSEA (Root Mean Square error of approximation: Steiger & Lind, 1980)です。 \[ \mathrm{RMSEA} = \sqrt{\max\left(\frac{L_h}{df_h} - \frac{1}{P-1},0\right)} \tag{7.45}\] TLIのところでも登場した\(\frac{L_{h}}{df_{h}}\)は「削減したパラメータ1個あたりの乖離度の大きさ」の指標です。 したがって,乖離度\(L_h\)が同じであれば,パラメータ数が少ない=自由度が大きいほど良い値になります。 RMSEAに関しては,0.05を下回っていると良いとか,90%信頼区間が0.1を含まないと良いなどと言われています。
倹約的指標には,他にもPGFI (parsimonious GFI: Mulaik et al., 1989)といったものもあります。 \[ \mathrm{PGFI} = \frac{df_h}{\frac{I(I-1)}{2}}\mathrm{GFI} \tag{7.46}\] ただ,PGFIはシンプルなモデルでは変動が大きすぎることがあります。 例えば 図 7.6 のモデルでは,10個の分散共分散を8個のパラメータで説明していましたが,この場合\(PGFI=\frac{2}{10}GFI\)となり,GFIの5分の1になってしまいます。 独立モデルだったとしても各変数の分散パラメータは必ず存在しているため,\(PGFI=\frac{6}{10}GFI\)となります。 ということで,PGFIと同様の補正がかかる倹約的指標では,どの程度の値なら十分かを明確に決めづらいためあまり使われることはない印象があります。
7.6.4 モデル比較の指標
適合度指標とは少し異なりますが,パラメータ数の割に当てはまりの良いモデルを選ぶための指標として情報量規準というものがあります。 代表的な情報量規準には \[ \begin{aligned} \mathrm{AIC} &= L_h - 2df_h \\ \mathrm{BIC} &= L_h - \log(P)df_h \end{aligned} \tag{7.47}\] などがあります (Akaike, 1969/1998–1969; Schwarz, 1978)。式からわかるように,パラメータ数が多くなるほど第2項の値が小さくなり,結果的に情報量規準の値が大きくなってしまいます。
情報量規準には絶対的な基準はありません。単体のモデルに対する値を見て一喜一憂するものではなく,複数のモデルにおける値を比較してより小さい方を選ぶためのものです。
一般的に,乖離度\(L_h\)はサンプルサイズが大きくなるほど大きな値になりやすいものです。 AICではパラメータを1つ追加した際のペナルティがサンプルサイズによらず2のため,サンプルサイズが大きくなるほど「パラメータを追加したことによる当てはまりの改善」のほうが「パラメータを追加したことによるペナルティ」よりも大きくなりやすく,結果的にパラメータ数の多いモデルを選びやすくなる,という性質があったりします。 また2つのモデルでの値の差がわずかな場合には,標本誤差によって大小関係が変わりうるため,単一の情報量規準だけを用いてモデルを選択するのは危険なときがあるかもしれません。 少しだけ注意しましょう。
7.6.5 確認してみよう
それでは,これまでに紹介したものを含めた様々な適合度指標をlavaanで出してみましょう。 fitmeasures()関数を使うと簡単に出すことが出来ます14。
npar fmin chisq
18.000 0.027 129.227
df pvalue baseline.chisq
18.000 0.000 2331.678
baseline.df baseline.pvalue cfi
28.000 0.000 0.952
tli nnfi rfi
0.925 0.925 0.914
nfi pnfi ifi
0.945 0.607 0.952
rni logl unrestricted.logl
0.952 -34146.289 -34081.676
aic bic ntotal
68328.579 68432.915 2432.000
bic2 rmsea rmsea.ci.lower
68375.725 0.050 0.042
rmsea.ci.upper rmsea.ci.level rmsea.pvalue
0.059 0.900 0.450
rmsea.close.h0 rmsea.notclose.pvalue rmsea.notclose.h0
0.050 0.000 0.080
rmr rmr_nomean srmr
0.308 0.308 0.036
srmr_bentler srmr_bentler_nomean crmr
0.036 0.036 0.041
crmr_nomean srmr_mplus srmr_mplus_nomean
0.041 0.036 0.036
cn_05 cn_01 gfi
544.308 656.021 0.987
agfi pgfi mfi
0.974 0.494 0.977
ecvi
0.068 これまでに紹介したもの以外にも色々出ていますが,とりあえず先ほど紹介したものに関する指標だけ説明すると
fitmeasures()関数で表示される適合度指標の一部
| 指標名 | 解説 |
|---|---|
chisq |
\(\chi^2\)統計量(\(L_h\)) |
df |
自由度(\(df_h\)) |
pvalue |
\(\chi^2\)検定の\(p\)値 |
baseline.*** |
独立モデルでの値(\(L_0,df_0\)) |
cfi |
CFI |
aic |
AIC |
bic |
BIC |
rmsea |
RMSEA |
rmsea.ci.lower |
RMSEAの90%信頼区間の下限 |
rmsea.ci.upper |
RMSEAの90%信頼区間の上限 |
rmsea.pvalue |
「RMSEAが0.05以下」という帰無仮説に対する\(p\)値 |
srmr |
SRMR |
gfi |
GFI |
agfi |
AGFI |
pgfi |
PGFI |
といった感じです。
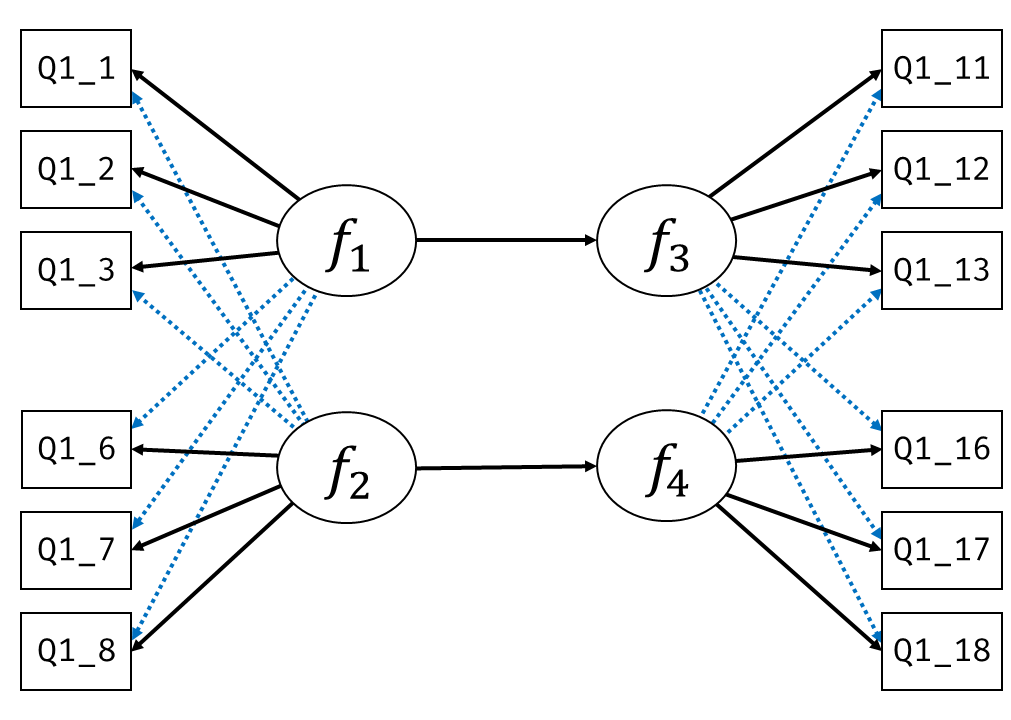
では実際に複数のモデルを比較して,各適合度指標の挙動を確認してみましょう。 ここでは,「正しい」モデルとして 図 7.3 の「本来の2因子モデル」を例として,これに「余計な矢印が入った2因子モデル」(「正しくない」モデル)と比較してみましょう。 まずは2つのモデルそれぞれについてパラメータ推定を行います。
続いて2つのモデルの適合度を比較していきましょう。 とはいえ,一つ一つfitmeasures()して出力を見比べるのは大変なので,複数のモデルの適合度を並べてくれるsemTools::compareFit()という関数を使ってみます。
semTools::compareFit(): 複数のモデルの適合度を比較する
################### Nested Model Comparison #########################
Chi-Squared Difference Test
Df AIC BIC Chisq Chisq diff RMSEA Df diff Pr(>Chisq)
result2 7 46682 46764 57.197
result1 8 46685 46761 62.062 4.8642 0.039861 1 0.02742 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
####################### Model Fit Indices ###########################
chisq df pvalue rmsea cfi tli srmr aic
result2 57.197† 7 .000 .054 .976† .949 .033† 46682.454†
result1 62.061 8 .000 .053† .974 .952† .035 46685.319
bic
result2 46763.605
result1 46760.673†
################## Differences in Fit Indices #######################
df rmsea cfi tli srmr aic bic
result1 - result2 1 -0.002 -0.002 0.003 0.002 2.864 -2.932最初のNested Model Comparisonというところは,ネストされたモデル間での比較です。 今回の例の場合,result1のモデルは,result2のモデルでf_1 =~ Q1_6の値が0になった場合という意味で,result2の特殊なケースといえます。 このように,あるモデルが別のモデルに内包されているとき,そのモデルは「ネスト」の関係にあると呼んだりします。
ネストされたたモデル間の比較では,尤度比検定を行うことができます。 ネストされたモデルでは,パラメータ数の減少に伴い少なからずデータに対する当てはまりが悪化(尤度が減少)しているはずですが,もしも尤度比検定が有意にならない場合,その当てはまりの悪化が「減らしたパラメータ数的に許容できる」という感じになり,それならばより節約的なモデルを選ぼう,という流れになります。 今回の場合,Pr(>Chisq)が0.05より小さいため検定は有意になっています。 result2を基準に見るとresult1のモデルはf_1 =~ Q1_6のパスを0にしたことによって当てはまりが有意に悪化している,ということです。 したがって,尤度比検定的にはresult2を選ぶべし,となります。 しかしこれも例によって統計的仮説検定あるあるの「サンプルサイズが大きいと有意になりやすい」があるので,これだけを信じすぎないほうが良いと思います。
その下のModel Fit Indicesでは各種適合度指標を並べてくれています。ダガー(†)の付いているものは,その適合度指標においてベストなモデル,という意味です。 また一番下のDifferences in Fit Indicesは読んで字のごとく適合度指標の差分です。 僅かな差ですが,RMSEAやTLIの値はf_1 =~ Q1_6のパスが無い(本来正しい)モデルの方が良い値です。 一方で絶対的指標であるCFIやSRMRはresult2のほうが良い値になっています。
情報量規準を見ると,AICはモデル2,BICはモデル1のほうが大きな値になっています。 先程説明したように,AICのほうがサンプルサイズが大きくなるほど複雑な(パラメータ数の多い)モデルを好む傾向があり,今回の比較でもその傾向が表れたということです。
このように,適合度指標の定義によってモデル比較の結果も一貫しないことが大半なので,結果を報告する際には複数の指標を提示し,総合的に判断する必要があるわけです。
compareFit()関数は,デフォルトでは上に表示されているいくつかの指標のみを表示する様になっています。 このSectionで紹介した他の適合度指標についても比較してほしい場合には,引数を設定する必要があります。
################### Nested Model Comparison #########################
Chi-Squared Difference Test
Df AIC BIC Chisq Chisq diff RMSEA Df diff Pr(>Chisq)
result2 7 46682 46764 57.197
result1 8 46685 46761 62.062 4.8642 0.039861 1 0.02742 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
####################### Model Fit Indices ###########################
gfi agfi rmsea.pvalue
result2 .992† .977 .271†
result1 .992 .978† .333
################## Differences in Fit Indices #######################
gfi agfi
result1 - result2 -0.001 0.001引数fit.measuresに指定できるのは,fitmeasures()関数で表示されるものの名前です。 そして実はfitmeasures()関数自体も同じ引数fit.measuresを受け付けるので,同様に一部の指標のみを表示したい場合には設定してあげると良いでしょう。
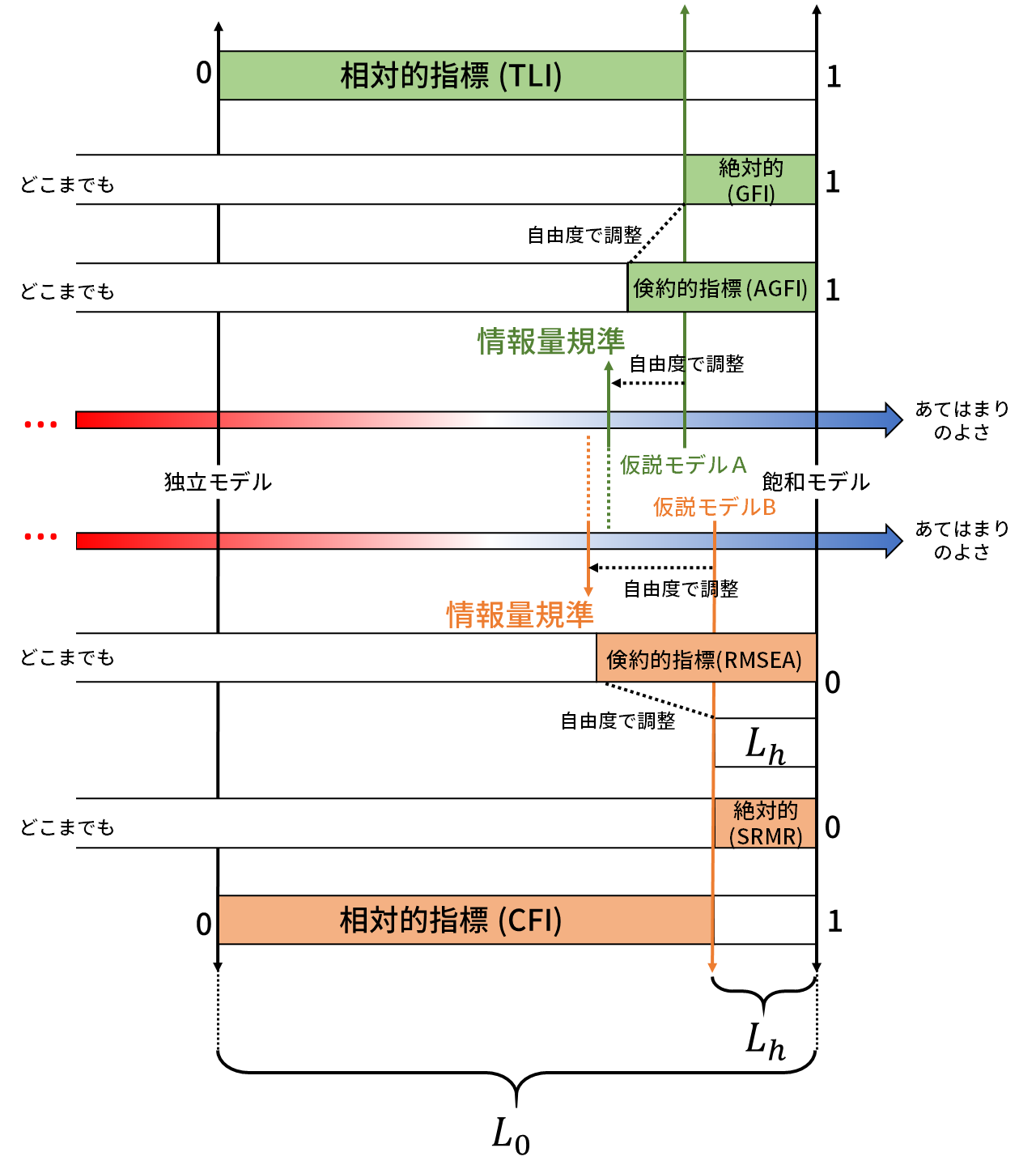
図 7.12 に,各種適合度指標の関係を表してみました。無理やり1つの図にまとめたので多少変なところがあるかもしれませんが…
- 相対的指標は「独立モデルを0,飽和モデルを1」としたときの仮説モデルの位置づけを表しています。
- 絶対的指標は「飽和モデル=データ」からのズレを表す指標です。理論上はたぶん下限は決まっていませんが,基本的に0から1の範囲内に収まるはずです。
- 倹約的指標はものによります。自由度で調整した値です。
- 情報量規準は独立モデル・飽和モデルと何の関係もありません。尤度を自由度で調整しただけです。図の例では,モデルBのほうが絶対的な当てはまりは良いのですが,自由度による調整の結果情報量規準の値はモデルAのほうが良い,という状態を表しています。
7.7 モデルの修正
(ここからはプラクティカルな話題です。)
SEMでは,まずドメイン知識に基づいた仮説を立てて,その仮説をモデルを落とし込んでいく(パス図に線を引く)ことになります。 そして,実際のデータと仮説モデルとで共分散行列がどの程度ずれているかを評価し,ズレが小さければ「問題ないモデル」と判断します。 ズレの大きさを評価する適合度指標には,大きく分けると「絶対的なズレの大きさを評価するもの(SRMRやGFIなど)」と「パラメータ数(自由度)を考慮して評価するもの(AGFIやRMSEA)」の2種類がありました。
もしも仮説モデルにおいて適合度指標の値が悪ければ,モデルを修正してデータとの整合性 and/or モデルの倹約度を高める必要があります。 データとの整合性を高めるためには,矢印を追加してあげれば良いです。 矢印を追加するということは推定するパラメータが増えるため,回帰分析の説明変数や因子分析の因子数を増やした時と同じように,パラメータを増やした分だけデータとモデルのズレは小さくできるはずです。 一方,モデルの倹約度を高めるためには矢印を消去する必要もあります。ある矢印が,あってもなくてもデータとモデルのズレに大きな影響を与えないのであれば,そのような矢印はなくなったほうがRMSEAなどは向上するはずです。
ということで,この節ではモデルを修正してデータとの整合性を高めるための方法について説明します。 手当たり次第にひとつひとつ矢印を足したり引いたりしたモデルを試しまくるのはさすがに効率が悪いので,もう少しスマートに修正案にアタリをつけたいと思います。 以降では, 図 7.8 のSEMモデルを題材にモデルの修正を試してみます。
lavaan 0.6-20 ended normally after 36 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 18
Number of observations 2432
Model Test User Model:
Test statistic 129.227
Degrees of freedom 18
P-value (Chi-square) 0.000
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_A =~
Q1_1 0.602 0.031 19.255 0.000 0.628 0.447
Q1_2 0.888 0.030 29.426 0.000 0.926 0.790
Q1_3 0.786 0.030 25.796 0.000 0.819 0.627
f_E =~
Q1_6 0.728 0.031 23.767 0.000 0.753 0.611
Q1_7 0.888 0.035 25.607 0.000 0.918 0.698
Q1_8 0.651 0.031 21.262 0.000 0.673 0.523
Regressions:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_A ~
age 0.014 0.002 6.275 0.000 0.013 0.147
gender 0.522 0.053 9.894 0.000 0.501 0.236
f_E ~
f_A 0.252 0.030 8.402 0.000 0.254 0.254
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
age ~~
gender 0.204 0.105 1.945 0.052 0.204 0.039
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Q1_1 1.581 0.051 31.144 0.000 1.581 0.801
.Q1_2 0.517 0.046 11.273 0.000 0.517 0.376
.Q1_3 1.034 0.046 22.666 0.000 1.034 0.607
.Q1_6 0.950 0.043 22.240 0.000 0.950 0.626
.Q1_7 0.889 0.055 16.228 0.000 0.889 0.513
.Q1_8 1.205 0.044 27.533 0.000 1.205 0.727
age 120.254 3.449 34.871 0.000 120.254 1.000
gender 0.221 0.006 34.871 0.000 0.221 1.000
.f_A 1.000 0.920 0.920
.f_E 1.000 0.935 0.935 npar fmin chisq
18.000 0.027 129.227
df pvalue baseline.chisq
18.000 0.000 2331.678
baseline.df baseline.pvalue cfi
28.000 0.000 0.952
tli nnfi rfi
0.925 0.925 0.914
nfi pnfi ifi
0.945 0.607 0.952
rni logl unrestricted.logl
0.952 -34146.289 -34081.676
aic bic ntotal
68328.579 68432.915 2432.000
bic2 rmsea rmsea.ci.lower
68375.725 0.050 0.042
rmsea.ci.upper rmsea.ci.level rmsea.pvalue
0.059 0.900 0.450
rmsea.close.h0 rmsea.notclose.pvalue rmsea.notclose.h0
0.050 0.000 0.080
rmr rmr_nomean srmr
0.308 0.308 0.036
srmr_bentler srmr_bentler_nomean crmr
0.036 0.036 0.041
crmr_nomean srmr_mplus srmr_mplus_nomean
0.041 0.036 0.036
cn_05 cn_01 gfi
544.308 656.021 0.987
agfi pgfi mfi
0.974 0.494 0.977
ecvi
0.068 7.7.1 不要なパスを消す
普通に考えると年齢ageと性別genderは無相関だと考えるのが自然ですね。 先程の分析の結果を見ても,共分散age ~~ genderの検定結果は有意にはなっていません。 summary(sem())で出力される検定では,帰無仮説に「そのパラメータの母数が0に等しい」を設定したWald検定の結果を出しています。 Wald検定の中身はともかく,とりあえずこのP(>|z|)列を見れば,そのパラメータを削除してよいかにアタリをつけられそうかが分かります。
ということで,検定結果が有意ではなかったage ~~ genderの共分散をゼロに固定して再度推定してみましょう。
lavaanの記法では,このように右辺の変数名の前に0*を付けると,そのパラメータの値を0に固定することが出来ます15。
lavaan 0.6-20 ended normally after 30 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 17
Number of observations 2432
Model Test User Model:
Test statistic 133.020
Degrees of freedom 19
P-value (Chi-square) 0.000
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_A =~
Q1_1 0.602 0.031 19.216 0.000 0.627 0.446
Q1_2 0.888 0.030 29.335 0.000 0.925 0.789
Q1_3 0.786 0.031 25.715 0.000 0.818 0.627
f_E =~
Q1_6 0.728 0.031 23.763 0.000 0.753 0.611
Q1_7 0.888 0.035 25.602 0.000 0.918 0.698
Q1_8 0.651 0.031 21.259 0.000 0.673 0.523
Regressions:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_A ~
age 0.014 0.002 6.280 0.000 0.013 0.147
gender 0.522 0.053 9.901 0.000 0.502 0.236
f_E ~
f_A 0.252 0.030 8.387 0.000 0.254 0.254
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
age ~~
gender 0.000 0.000 0.000
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Q1_1 1.581 0.051 31.136 0.000 1.581 0.801
.Q1_2 0.517 0.046 11.237 0.000 0.517 0.377
.Q1_3 1.034 0.046 22.625 0.000 1.034 0.607
.Q1_6 0.950 0.043 22.238 0.000 0.950 0.626
.Q1_7 0.889 0.055 16.225 0.000 0.889 0.513
.Q1_8 1.205 0.044 27.532 0.000 1.205 0.727
age 120.254 3.449 34.871 0.000 120.254 1.000
gender 0.221 0.006 34.871 0.000 0.221 1.000
.f_A 1.000 0.923 0.923
.f_E 1.000 0.936 0.936結果を見ると,確かに共分散age ~~ genderの値が推定されず,0に固定されています。 それでは,パス削除前(result1)と削除後(result2)の適合度を比較してみましょう。
################### Nested Model Comparison #########################
Chi-Squared Difference Test
Df AIC BIC Chisq Chisq diff RMSEA Df diff Pr(>Chisq)
result1 18 68329 68433 129.23
result2 19 68330 68429 133.02 3.7929 0.033888 1 0.05147 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
####################### Model Fit Indices ###########################
chisq df pvalue rmsea cfi tli srmr aic
result1 129.227† 18 .000 .050 .952† .925 .036† 68328.579†
result2 133.020 19 .000 .050† .951 .927† .037 68330.371
bic
result1 68432.915
result2 68428.911†
################## Differences in Fit Indices #######################
df rmsea cfi tli srmr aic bic
result2 - result1 1 -0.001 -0.001 0.002 0.001 1.793 -4.004いま比較している2つのモデルのうちresult2のモデルは,result1のモデルでage ~~ genderの値が0になった場合という意味で,result1の特殊なケースといえます。 ということで尤度比検定の結果が出力されています。 今回の場合,Pr(>Chisq)が0.05より大きいため検定は(ギリギリ)有意になっていません。 したがって,尤度比検定的にはパラメータを1つ削除しても当てはまりは有意には悪化していない,そのためより節約的なresult2を選ぼう,ということになるわけです。
続いて各種適合度指標を見ると,僅かな差ですが,RMSEAやTLIの値は改善しているようです。 一方で絶対的指標であるSRMRは悪化しているようですね。
このように,単一のパスを削除する場合には,cfa()やsem()の結果の検定のところを見るのが第一歩です。 ですが,統計的仮説検定の枠組みの中にあるため,サンプルサイズの影響を受けてしまう点は注意が必要です。 例えば先程の分析を,サンプルサイズを100人にして行うと,さっきは有意だったf_A ~ ageの回帰係数も有意ではなくなってしまいます。 検定の結果だけを鵜呑みにするのではなく,例えば実際の推定値の大きさを踏まえて決定するなどの対応が必要でしょう。
lavaan 0.6-20 ended normally after 35 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 18
Number of observations 100
Model Test User Model:
Test statistic 29.972
Degrees of freedom 18
P-value (Chi-square) 0.038
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_A =~
Q1_1 0.535 0.151 3.540 0.000 0.576 0.394
Q1_2 0.926 0.147 6.301 0.000 0.996 0.857
Q1_3 0.674 0.141 4.781 0.000 0.725 0.537
f_E =~
Q1_6 0.764 0.126 6.085 0.000 0.840 0.679
Q1_7 0.829 0.135 6.163 0.000 0.911 0.690
Q1_8 0.822 0.132 6.222 0.000 0.904 0.698
Regressions:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_A ~
age 0.011 0.010 1.050 0.294 0.010 0.115
gender 0.720 0.254 2.830 0.005 0.669 0.330
f_E ~
f_A 0.424 0.148 2.874 0.004 0.415 0.415
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
age ~~
gender 1.028 0.580 1.772 0.076 1.028 0.180
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Q1_1 1.801 0.273 6.606 0.000 1.801 0.844
.Q1_2 0.360 0.234 1.535 0.125 0.360 0.266
.Q1_3 1.296 0.225 5.769 0.000 1.296 0.711
.Q1_6 0.823 0.172 4.788 0.000 0.823 0.539
.Q1_7 0.915 0.197 4.647 0.000 0.915 0.524
.Q1_8 0.860 0.190 4.533 0.000 0.860 0.513
age 133.886 18.934 7.071 0.000 133.886 1.000
gender 0.244 0.034 7.071 0.000 0.244 1.000
.f_A 1.000 0.864 0.864
.f_E 1.000 0.828 0.8287.7.2 新しいパスを増やす
続いて,新しいパスを追加することを考えたいと思います。 パスを追加する場合,基本的に絶対的な適合度は上昇するため,先程の尤度比検定の考え方とは反対に「パラメータを1個追加する価値があるだけの適合度の改善が見られる」ようなパラメータは追加してあげればよいわけです。 modificationIndices()という関数は,現状モデル内でパラメータが自由推定になっていない全てのパス16について,「そこにパスを追加するとどれだけ適合度が改善するか」をまとめて表してくれます。
lhs op rhs mi epc sepc.lv sepc.all sepc.nox
24 f_E =~ Q1_1 33.281 -0.196 -0.203 -0.144 -0.144
32 Q1_1 ~~ age 25.661 1.519 1.519 0.110 0.110
37 Q1_2 ~~ Q1_8 23.532 0.114 0.114 0.145 0.145
45 Q1_6 ~~ Q1_7 19.848 0.527 0.527 0.574 0.574
23 f_A =~ Q1_8 19.845 0.134 0.139 0.108 0.108
47 Q1_6 ~~ age 13.741 0.902 0.902 0.084 0.084
30 Q1_1 ~~ Q1_7 9.220 -0.092 -0.092 -0.078 -0.078
33 Q1_1 ~~ gender 9.153 0.040 0.040 0.068 0.068
26 f_E =~ Q1_3 7.717 0.087 0.089 0.069 0.069
43 Q1_3 ~~ age 6.496 -0.690 -0.690 -0.062 -0.062
50 Q1_7 ~~ age 6.371 -0.645 -0.645 -0.062 -0.062
41 Q1_3 ~~ Q1_7 5.463 0.062 0.062 0.065 0.065
[ reached 'max' / getOption("max.print") -- omitted 32 rows ]引数sort = TRUEを与えると,改善度(出力の一番左,mi列)の大きい順に並べてくれます。 したがって今回の場合,一つだけパスを追加するならばf_E =~ Q1_1というパスを追加すると適合度が最も改善する,ということです。 出力ではmi列に続いて,
epc- そのパスを自由推定にした際のパラメータの変化量の予測値。パスが引かれていない場合は「0からの変化量」なので推定値そのものの予測値を意味する。
sepc.lv-
潜在変数
lvを標準化した際のEPC (standardized EPC)。 sepc.all- 全ての変数を標準化した際(標準化解)のEPC。
sepc.nox- 観測変数の外生変数以外を全て標準化した際のEPC。
が表示されています。きっと多くの場合ではmiが大きいところはsepc.allが大きくなっていることでしょう。 ということで,パスを追加する際にはmiが大きいほうから試してみると良いでしょう。 さっそくf_E =~ Q1_1を追加して推定してみます。
lavaan 0.6-20 ended normally after 31 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 18
Number of observations 2432
Model Test User Model:
Test statistic 98.800
Degrees of freedom 18
P-value (Chi-square) 0.000
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_A =~
Q1_1 0.678 0.034 19.682 0.000 0.707 0.503
Q1_2 0.867 0.029 29.957 0.000 0.904 0.772
Q1_3 0.792 0.030 26.483 0.000 0.826 0.633
f_E =~
Q1_6 0.720 0.030 23.860 0.000 0.752 0.610
Q1_7 0.879 0.034 25.758 0.000 0.918 0.698
Q1_8 0.647 0.030 21.333 0.000 0.675 0.524
Q1_1 -0.201 0.034 -5.875 0.000 -0.210 -0.149
Regressions:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_A ~
age 0.014 0.002 6.466 0.000 0.014 0.152
gender 0.529 0.053 9.982 0.000 0.507 0.238
f_E ~
f_A 0.287 0.031 9.131 0.000 0.287 0.287
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
age ~~
gender 0.000 0.000 0.000
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Q1_1 1.514 0.052 29.360 0.000 1.514 0.767
.Q1_2 0.555 0.042 13.069 0.000 0.555 0.404
.Q1_3 1.021 0.044 23.011 0.000 1.021 0.600
.Q1_6 0.952 0.042 22.594 0.000 0.952 0.628
.Q1_7 0.889 0.054 16.558 0.000 0.889 0.513
.Q1_8 1.202 0.044 27.589 0.000 1.202 0.725
age 120.254 3.449 34.871 0.000 120.254 1.000
gender 0.221 0.006 34.871 0.000 0.221 1.000
.f_A 1.000 0.920 0.920
.f_E 1.000 0.918 0.918パス追加前(result2)と追加後(result3)の適合度を比較してみましょう。
################### Nested Model Comparison #########################
Chi-Squared Difference Test
Df AIC BIC Chisq Chisq diff RMSEA Df diff Pr(>Chisq)
result3 18 68298 68402 98.80
result2 19 68330 68429 133.02 34.22 0.11688 1 4.921e-09 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
####################### Model Fit Indices ###########################
chisq df pvalue rmsea cfi tli srmr aic
result3 98.800† 18 .000 .043† .965† .945† .029† 68298.151†
result2 133.020 19 .000 .050 .951 .927 .037 68330.371
bic
result3 68402.488†
result2 68428.911
################## Differences in Fit Indices #######################
df rmsea cfi tli srmr aic bic
result2 - result3 1 0.007 -0.014 -0.018 0.008 32.22 26.424尤度比検定の結果は有意になっています。今回はresult2のほうが節約的なモデルなので,パス追加前(result2)の方が当てはまりが有意に悪い,ということになりました。 ほかの適合度指標を見ても,どうやら確かに追加したあとの方が改善しているようです。
7.7.3 実際のところ
ここまで,モデルを修正するための候補を統計的な視点から紹介しました。 しかしSEMで重要なのは,因子分析と同じようにその結果をきちんと解釈できるか(解釈可能性)です。 実際にモデルを修正するかどうかは,そのパスが持つ意味をよく考えて行う必要があります。 先程の修正では,f_E =~ Q1_1を追加したことによって 図 7.13 のような状態になりました。 つまり完全な単純構造ではないと考えたほうがデータ的には当てはまりが良い,ということです。 ですが修正指標(mi)も,尤度に基づく指標です。つまりサンプルサイズが大きいほど当てはまりは大幅に改善するように見えてしまいます。 したがって,本質的には無意味なパスが手元のデータにおいては偶然それなりの改善を示しただけの可能性もあります。 同様に,モデルが複雑になるほど自由度も大きくなり共分散構造の乖離度も大きくなりやすいと考えられます。 「f_E =~ Q1_1を追加すると良い」ということが,本当に「Q1_1が因子Eを反映した項目である」ことを示しているのかは,実質的な意味に基づいてよく考える必要があるでしょう。
ということで,モデルの修正の際には,パスを追加・削除することが自分の仮説と照らし合わせて受け入れられるかをよく考えるようにしましょう。
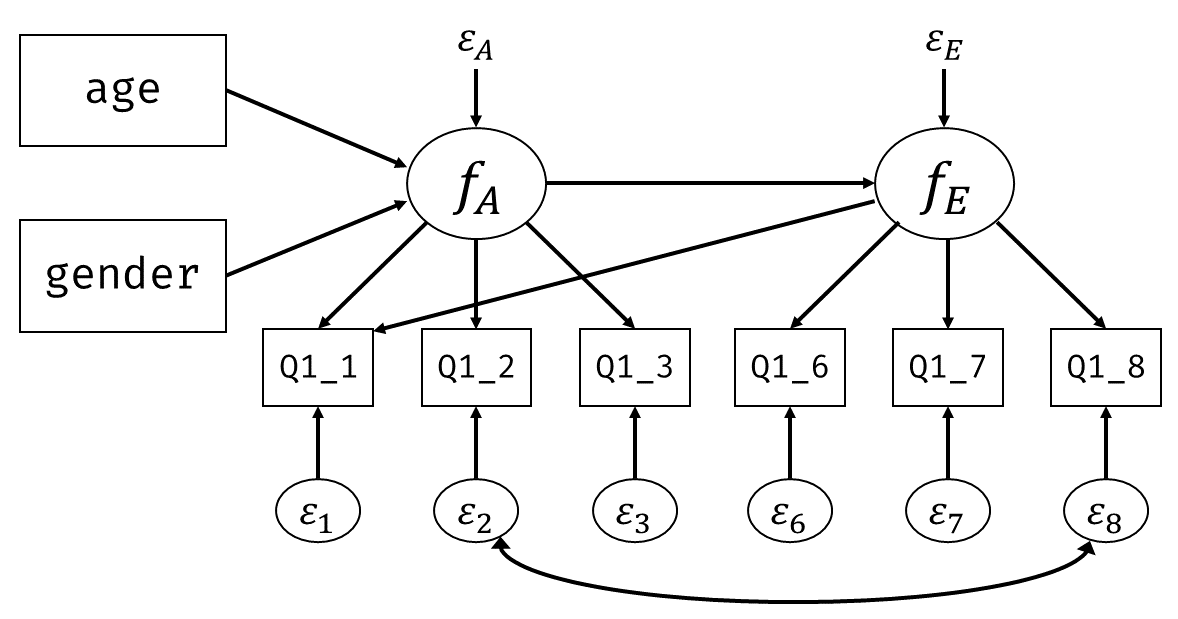
実践場面でよく見られる―が適切に用いられていないことも多い(吉田 他,2020)―修正としては, 図 7.14 のように独自因子の間の相関を追加するパターンがあります。 例えば時系列モデルにおいて,異なる時期に聞かれた同一の項目間においたり,あるいはDIFのように特定の属性などが影響していると言えそうな場合には妥当なパスの追加だと思われます。 このような場合にも,パスを追加する場合にはなぜそのパスを追加するべき(しても問題ない)と考えたかをきちんと説明するようにしましょう。 裏を返せば,そのパスが意味するところが説明できないような場所には,いくら適合度が改善するにしてもパスを追加しないほうが良いだろう,ということです。
また,モデルの修正は割と終わりなき戦いです。 というのも,modificationIndices()で出力されるmiは必ず正の値を取ります。 絶対的な適合度指標と同じように,パスを追加すればするほど当てはまりは良くなるということです。 モデルの修正を行う場合には,
- まず仮説で立てたモデルを基準として
- もしそのままでは当てはまりが良くない(適合度指標が許容範囲を超えている)という場合にのみ
- もともとの仮説で受け入れられるパスの追加・削除を少しずつ行い
- 適合度指標が許容範囲になったらその時点でストップ
くらいに考えておくのが良いのではないかと思います。多くの場合は仮説で立てたモデルが(本当に考え抜いて構築されたのならば)理論的には最も整合的なはずなので,そこからあまり変えないようにできればそれに越したことは無いわけです。 適合度指標の許容範囲についてはゼロイチで判断できるものではないですが,自分が納得できる&査読者などを納得させられるくらいの値であれば良いでしょう。
7.8 カテゴリカル変数のSEM
資料の前半で見てきたように,SEMは因子分析や回帰分析を内包する分析手法です。 したがって,カテゴリカル変数を扱う場合も因子分析や回帰分析と同じように考えればOKです。
7.8.1 内生変数がカテゴリカルな回帰分析・パス解析
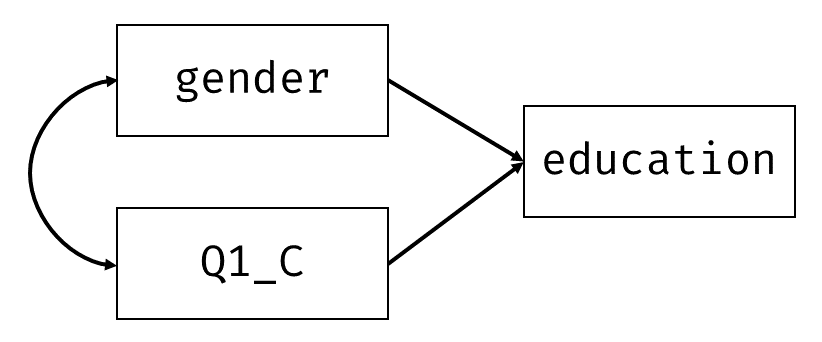
内生変数,つまり結果変数がカテゴリカルな場合,ポリコリック相関のように,本来連続的なものが閾値で切り分けられてカテゴリになっている,と考えると良さそうです。 ここでは, 図 7.15 のように,性別と勤勉性(Q1_C)がカテゴリカルな内生変数である「学歴」に与える影響を考える回帰分析モデルを実行してみましょう17。
lavaanには,内生観測変数がカテゴリカルであることを示す引数orderedが用意されています。
lavaan 0.6-20 ended normally after 3 iterations
Estimator DWLS
Optimization method NLMINB
Number of model parameters 6
Used Total
Number of observations 2232 2432
Model Test User Model:
Standard Scaled
Test Statistic 0.000 0.000
Degrees of freedom 0 0
Parameter Estimates:
Parameterization Delta
Standard errors Robust.sem
Information Expected
Information saturated (h1) model Unstructured
Regressions:
Estimate Std.Err z-value P(>|z|)
education ~
gender 0.007 0.047 0.150 0.881
Q1_C 0.006 0.005 1.233 0.217
Thresholds:
Estimate Std.Err z-value P(>|z|)
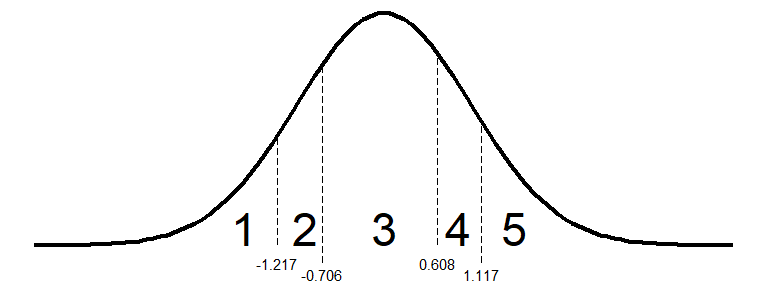
education|t1 -1.217 0.123 -9.858 0.000
education|t2 -0.706 0.123 -5.757 0.000
education|t3 0.608 0.124 4.914 0.000
education|t4 1.117 0.125 8.961 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.education 1.000 結果を見ると,Variances:のところにあるeducationに,潜在変数であることを示す.がついて.educationになっており,その値が1に固定されています。 また,表示はされていないのですが,.educationの平均値は自動的に0に固定されてパラメータ推定が行われます18。 すなわちカテゴリカルな内生変数を扱う場合には,その変数(ここではeducation)の背後にある連続的なものが平均0,分散1に標準化された値として考慮されている,ということです。
そのもとで,Thresholds:のところには各カテゴリの閾値が表示されています。図4.8に当てはめると 図 7.16 のような状態だということです。
7.8.2 (おまけ)外生変数がカテゴリカルな回帰分析・パス解析
「外生変数がカテゴリカル」ということは,回帰分析の説明変数がカテゴリカルな場合と同じように考えたらOKです。 すなわち,その変数が二値カテゴリカルであればそのまま使用してよく,多値カテゴリカルであればダミー変数に置き換えることで対応可能です。 例えば多値カテゴリカル変数であるeducationを説明変数とする, 図 7.17 の回帰分析モデルを考えます。
educationは順序カテゴリカル変数ですが,いったん順序を無視してダミー変数へ変換してみます(順序性を考慮したダミー変数化はあとで説明)。 ダミー変数をデータフレームに追加する簡単な方法として,contr.treatment()関数を利用する方法があります19。
contr.treatment()関数では第一カテゴリを基準カテゴリとしたダミー変数を作成してくれます。
2 3 4 5
<NA> NA NA NA NA
<NA> NA NA NA NA
<NA> NA NA NA NA
<NA> NA NA NA NA
<NA> NA NA NA NA
3 0 1 0 0
<NA> NA NA NA NA
2 1 0 0 0
<NA> NA NA NA NA
1 0 0 0 0
<NA> NA NA NA NA
<NA> NA NA NA NA
1 0 0 0 0
<NA> NA NA NA NA
<NA> NA NA NA NA
<NA> NA NA NA NA
<NA> NA NA NA NA
<NA> NA NA NA NA
<NA> NA NA NA NA
<NA> NA NA NA NA
5 0 0 0 1
2 1 0 0 0
1 0 0 0 0
3 0 1 0 0
5 0 0 0 1
[ reached 'max' / getOption("max.print") -- omitted 2407 rows ]contr.treatment()で作成したダミー行列のdat$education行目を取る,ということは,
education == 1の人なら0 0 0 0の行education == 2の人なら1 0 0 0の行education == 3の人なら0 1 0 0の行education == 4の人なら0 0 1 0の行education == 5の人なら0 0 0 1の行education == NAの人ならNA NA NA NAの行
が返ってくるわけです。これをもとのdatの存在しない列名に代入してあげればOKですね。
こうして作成したダミー変数を入れたモデルを作成して実行しましょう。
lavaan 0.6-20 ended normally after 1 iteration
Estimator ML
Optimization method NLMINB
Number of model parameters 7
Used Total
Number of observations 2232 2432
Model Test User Model:
Test statistic 0.000
Degrees of freedom 0
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Regressions:
Estimate Std.Err z-value P(>|z|)
Q1_A ~
age 0.068 0.009 7.470 0.000
edu_2 -0.207 0.417 -0.497 0.619
edu_3 1.097 0.336 3.263 0.001
edu_4 -0.132 0.393 -0.337 0.736
edu_5 0.413 0.394 1.046 0.295
Intercepts:
Estimate Std.Err z-value P(>|z|)
.Q1_A 20.897 0.382 54.641 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.Q1_A 18.842 0.564 33.407 0.000Number of observationsのところにTotalという値が追加されています。 当然ですが欠測値がある場合にはそのままだと分析が出来ないため,デフォルトでは「分析に使用する変数に欠測が一つもない人」だけを使って分析をしているのです。 今回の場合,education == NAの人は全てのダミー変数がNAになっているので,「educationに回答している人のデータのみ」を使用した結果となっている点には注意が必要かもしれません。
順序カテゴリの順序性を保ったままダミー化する場合は,下の表のようにダミーの効果を加算していく,という方法が考えられます。 カテゴリ2ではedu_2の効果のみ,カテゴリ3ではedu_2 + edu_3の効果,…というようになります。 そして例えばedu_3の係数は,education == 2の人とeducation == 3の人の切片の差を表すことになるわけです。
| education | edu_2 | edu_3 | edu_4 | edu_5 |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 |
| 2 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 |
| 4 | 1 | 1 | 1 | 0 |
| 5 | 1 | 1 | 1 | 1 |
7.8.3 カテゴリカルな確認的因子分析
確認的因子分析の場合,モデル上は因子得点から観測変数に矢印が引かれているため,これらは全て内生変数として扱われます。したがって引数orderedを使えばOKです。 ということで,前回行った 図 7.3 の単純構造2因子モデルで試してみましょう。
全ての変数を名指しでordered=paste0("Q1_",c(1,2,3,6,7,8))という感じで指定しても良いのですが,もし全ての内生変数である観測変数がカテゴリの場合20,ordered = TRUEとすることで全てカテゴリカルになります。
# まずは普通にモデル式を作成
model <- "
f_1 =~ Q1_1 + Q1_2 + Q1_3
f_2 =~ Q1_6 + Q1_7 + Q1_8
"
# 引数orderedを指定する
result <- cfa(model, data = dat, std.lv = TRUE, ordered = TRUE)
summary(result, standardized = TRUE)lavaan 0.6-20 ended normally after 14 iterations
Estimator DWLS
Optimization method NLMINB
Number of model parameters 37
Number of observations 2432
Model Test User Model:
Standard Scaled
Test Statistic 72.885 100.302
Degrees of freedom 8 8
P-value (Chi-square) 0.000 0.000
Scaling correction factor 0.733
Shift parameter 0.815
simple second-order correction
Parameter Estimates:
Parameterization Delta
Standard errors Robust.sem
Information Expected
Information saturated (h1) model Unstructured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_1 =~
Q1_1 0.472 0.020 24.163 0.000 0.472 0.472
Q1_2 0.854 0.021 41.558 0.000 0.854 0.854
Q1_3 0.681 0.019 36.343 0.000 0.681 0.681
f_2 =~
Q1_6 0.649 0.020 32.847 0.000 0.649 0.649
Q1_7 0.729 0.019 37.962 0.000 0.729 0.729
Q1_8 0.561 0.018 30.590 0.000 0.561 0.561
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_1 ~~
f_2 0.271 0.027 10.191 0.000 0.271 0.271
Thresholds:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
Q1_1|t1 -1.887 0.051 -36.934 0.000 -1.887 -1.887
Q1_1|t2 -1.234 0.034 -36.437 0.000 -1.234 -1.234
Q1_1|t3 -0.743 0.028 -26.414 0.000 -0.743 -0.743
Q1_1|t4 -0.326 0.026 -12.588 0.000 -0.326 -0.326
Q1_1|t5 0.434 0.026 16.487 0.000 0.434 0.434
Q1_2|t1 -2.144 0.064 -33.743 0.000 -2.144 -2.144
Q1_2|t2 -1.534 0.040 -38.430 0.000 -1.534 -1.534
Q1_2|t3 -1.179 0.033 -35.716 0.000 -1.179 -1.179
Q1_2|t4 -0.478 0.027 -18.047 0.000 -0.478 -0.478
Q1_2|t5 0.481 0.027 18.127 0.000 0.481 0.481
Q1_3|t1 -1.829 0.049 -37.433 0.000 -1.829 -1.829
Q1_3|t2 -1.303 0.035 -37.181 0.000 -1.303 -1.303
Q1_3|t3 -0.963 0.030 -31.885 0.000 -0.963 -0.963
Q1_3|t4 -0.328 0.026 -12.668 0.000 -0.328 -0.328
[ reached 'max' / getOption("max.print") -- omitted 16 rows ]
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Q1_1 0.777 0.777 0.777
.Q1_2 0.270 0.270 0.270
.Q1_3 0.536 0.536 0.536
.Q1_6 0.578 0.578 0.578
.Q1_7 0.469 0.469 0.469
.Q1_8 0.686 0.686 0.686
f_1 1.000 1.000 1.000
f_2 1.000 1.000 1.000orderedを指定せずにやった結果と比べると,因子負荷の値(Std.all列)が少し大きくなっていることがわかります。 このあたりは探索的因子分析のときと同じですね。
7.9 多母集団同時分析
分析結果の一般化可能性を高めるためには「異なる属性間で一貫して同じ結果が得られるか」を検討するのが一つの手段となります。 あるいは異なる属性・集団の間での差異に関心がある場合にも,グループごとに分析を行い結果の一貫性を検討することが多々あります。 例えば因子分析によって得られる因子得点に関して,男性と女性で平均点に差があるか・どちらのほうが平均点が高いかを検討したいとしましょう。 SEMでは多母集団同時分析という枠組みによってこうした分析を行うことができます。
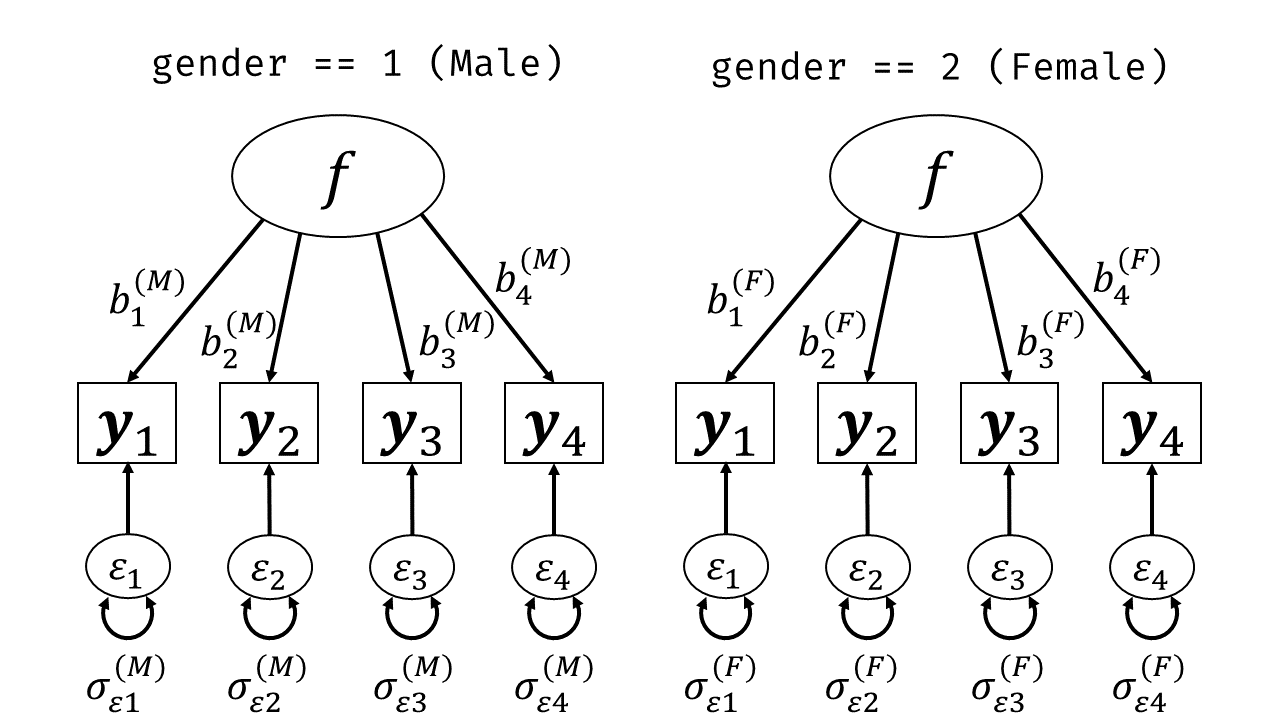
7.9.1 多母集団同時分析の基本的な考え方
基本的な考え方はシンプルです。 図 7.18 のように,まずデータをグループごとに分けておいて,同じモデルをグループごとに適用し,対応するパラメータの推定値が同じかどうかを評価していきます。 なおここでは,上付き添字はグループごとに異なる係数を表すと思ってください。 つまり\(b_1^{(M)}\)と\(b_1^{(F)}\)は同じ因子から同じ項目への因子負荷ですが,異なるパラメータとして別々に推定される,ということです。
lavaanでは,引数groupに,グループを表す変数の名前を指示してあげればすぐに分析が可能です。
lavaan 0.6-20 ended normally after 43 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 24
Number of observations per group:
1 802
2 1630
Model Test User Model:
Test statistic 34.458
Degrees of freedom 4
P-value (Chi-square) 0.000
Test statistic for each group:
1 7.472
2 26.986
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Group 1 [1]:
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_A =~
Q1_1 0.549 0.058 9.544 0.000 0.549 0.385
Q1_2 0.857 0.051 16.813 0.000 0.857 0.682
Q1_3 0.965 0.054 17.784 0.000 0.965 0.731
Q1_4 0.761 0.059 13.003 0.000 0.761 0.515
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Q1_1 4.278 0.050 85.060 0.000 4.278 3.004
.Q1_2 4.494 0.044 101.352 0.000 4.494 3.579
.Q1_3 4.347 0.047 93.246 0.000 4.347 3.293
.Q1_4 4.434 0.052 84.932 0.000 4.434 2.999
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Q1_1 1.728 0.093 18.624 0.000 1.728 0.852
.Q1_2 0.842 0.070 11.949 0.000 0.842 0.534
.Q1_3 0.811 0.082 9.916 0.000 0.811 0.465
.Q1_4 1.607 0.094 17.037 0.000 1.607 0.735
f_A 1.000 1.000 1.000
Group 2 [2]:
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_A =~
Q1_1 0.575 0.039 14.834 0.000 0.575 0.420
Q1_2 0.811 0.032 25.073 0.000 0.811 0.738
Q1_3 0.852 0.037 23.087 0.000 0.852 0.665
Q1_4 0.695 0.041 16.883 0.000 0.695 0.474
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Q1_1 4.748 0.034 139.992 0.000 4.748 3.467
.Q1_2 4.953 0.027 182.102 0.000 4.953 4.510
.Q1_3 4.728 0.032 149.135 0.000 4.728 3.694
.Q1_4 4.818 0.036 132.828 0.000 4.818 3.290
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Q1_1 1.544 0.059 26.000 0.000 1.544 0.824
.Q1_2 0.549 0.041 13.298 0.000 0.549 0.455
.Q1_3 0.913 0.052 17.571 0.000 0.913 0.557
.Q1_4 1.662 0.066 25.038 0.000 1.662 0.775
f_A 1.000 1.000 1.000結果を見ると,Number of observations per group:(7行目)のところで,各グループでの人数を表示しています。 そしてGroup 1 [1]:(27行目から)とGroup 2 [2]:(54行目から)という形で,それぞれのグループに対する推定結果が表示されています。
ただしこの段階では,単にデータを分割してそれぞれ独立にパラメータ推定を行っただけなので,グループごとに因子得点が標準化されています(52, 78行目)。 そのため,当然ながら平均値などの比較はできません。 そして因子得点をグループ間で比較可能にするためには,因子負荷と切片がともにグループ間で等しいという制約を置く必要があります。 多母集団同時分析の目的の一つは,因子構造が同じかどうかを検証することですが,同一性が満たされて初めて,異なるグループ間での因子得点の平均が比較可能になります。
因子負荷が等しいという条件は,そもそも因子自体がグループ間で異なっていないことを示すために必要です。これが満たされていないと,(仮にモデルの矢印が同じであっても)因子に占める各項目の重みが変わってしまうため,完全に同じ因子とは言えないのです。
では,切片が同じという制約はなぜ必要なのでしょうか。 ここでいう「切片」は,回帰分析の「切片」と同じようなものです。 因子分析では説明変数にあたる因子得点が潜在変数のため,少し厄介なことになっているのです。 これまで1因子の因子分析モデルは \[ \symbf{y}_i = \symbf{f}b_{i} + \symbf{\varepsilon}_i \tag{7.48}\] という形を取っていました。 ですが本当は,回帰分析での\(b_0\)にあたる切片項(ここでは\(\tau\)と表記します)が存在しており, \[ \symbf{y}_i = \tau + \symbf{f}b_{i} + \symbf{\varepsilon}_i \tag{7.49}\] という式になっています。 通常SEM(因子分析)では,観測変数\(\symbf{y}_i\)は標準化されていれば(あるいは標準化解を出す場合には),暗黙に\(\tau=0\)となります。そのためにこれまでは\(\tau\)を無視してきました。 ですが多母集団同時分析では,観測変数\(\symbf{y}_i\)が標準化されていたとしても,切片項まで考慮しないと因子得点の比較ができなくなってしまいます21。
例えば,データ全体で標準化された(全体平均が0の)観測変数\(\symbf{y}_i\)の平均値が,男性のみで計算すると0.3, 女性のみで計算すると-0.3だった,つまり男性のほうが平均的に高い得点をつけていたとしましょう。 これは心理尺度で言えば,男性のほうが「当てはまる」寄りの回答をしがち,という状況に相当します。 そう考えるとこの0.6の差は「男性のほうが関連する因子得点\(\symbf{f}\)が高い」ということを意味しているように見えるかもしれませんが,まだそうではない可能性を持っています。 もしグループごとに異なる切片\(\tau^{(g)}\)があるとすると,先程の式は \[
\symbf{y}_i = \tau^{(g)} + \symbf{f}b_{i} + \symbf{\varepsilon}_i
\tag{7.50}\] となります。 ここで,もし男性の切片\(\tau^{(\mathrm{M})}=0.3\)で女性の切片\(\tau^{(\mathrm{F})}=-0.3\)だとすると,観測変数\(\symbf{y}_i\)の平均値の差0.6は切片の差に起因するものになってしまい,因子得点\(\symbf{f}\)の部分では平均値には差がなくなります。 これは回帰分析で言えばgenderというダミー変数に対する回帰係数が0.6だった,ということです。 例えばその項目が因子とは別の理由で男性の方が「あてはまる」と答えやすい項目(つまりDIF)などのケースでは,こういったことが起こると考えられます。 そこで,もし\(\tau^{(\mathrm{M})}=\tau^{(\mathrm{F})}\)という制約をおけば,観測変数\(\symbf{y}_i\)の平均値の差0.6は因子得点\(\symbf{f}\)のほうに表れてくれる,というわけです。 こういった理由から,グループ間で因子得点を比較可能にするためには,因子負荷だけでなく切片にも等値制約を置く必要があるのです。
7.9.2 測定不変性の検証
多母集団同時分析では,先程実行した「グループ間でモデル式までは同じ」モデル(配置不変モデル:configural invarianceなどと呼ばれます)をベースラインとして,グループ間で等値制約をどこまで追加しても当てはまりが悪化しないかを検証していきます。 ということで,もし配置不変モデルの段階で適合度が悪かったら終了です。 そのような場合は,少なくともgroupで分ける前から適合度が悪いはず…
配置不変モデルの適合度が問題なければ制約を追加していきましょう。 ここからは
- 【弱測定不変モデル:weak invariance】 因子負荷が同じ
- 【強測定不変モデル:strong invariance】 さらに切片が同じ
- 【厳密な測定不変モデル:strict invariance】 さらに独自因子の分散(共分散)が同じ
- 【(ほぼ完全な測定不変モデル)】 さらに共通因子の分散共分散が同じ
- 【(完全な測定不変モデル)】 さらに因子得点の平均が同じ
という順番で徐々に制約を追加していきます22。 つまり最低でも強測定不変モデルが許容されるならば,因子得点の平均の比較が可能になるというわけです。 また,もしも一番下までクリア出来てしまった場合には,多母集団同時分析を行う必要はありません。その場合には,胸を張って単一母集団モデルとしての結果を報告しましょう。
lavaanでこれらの等値制約をかける場合には,引数group.equalに制約をかけたいパラメータの種類を指定します。指定は何種類でもOKです。
group.equalで指定できる等値制約
| 指定 | 制約されるもの |
|---|---|
loadings |
因子負荷 |
intercepts |
切片 |
means |
因子得点の平均 |
thresholds |
閾値(orderedのときの) |
regressions |
回帰係数 |
residuals |
独自因子の分散 |
residual.covariances |
独自因子の共分散 |
lv.variance |
共通因子の分散 |
lv.covariance |
共通因子の共分散 |
ということで,まずは弱測定不変モデル(因子負荷が同じ)を実行してみます。
lavaan 0.6-20 ended normally after 43 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 25
Number of equality constraints 4
Number of observations per group:
1 802
2 1630
Model Test User Model:
Test statistic 35.926
Degrees of freedom 7
P-value (Chi-square) 0.000
Test statistic for each group:
1 8.416
2 27.509
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Group 1 [1]:
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_A =~
Q1_1 (.p1.) 0.596 0.038 15.684 0.000 0.596 0.415
Q1_2 (.p2.) 0.869 0.039 22.169 0.000 0.869 0.692
Q1_3 (.p3.) 0.937 0.042 22.576 0.000 0.937 0.714
Q1_4 (.p4.) 0.756 0.041 18.308 0.000 0.756 0.512
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Q1_1 4.278 0.051 84.317 0.000 4.278 2.977
.Q1_2 4.494 0.044 101.301 0.000 4.494 3.577
.Q1_3 4.347 0.046 93.738 0.000 4.347 3.310
.Q1_4 4.434 0.052 84.975 0.000 4.434 3.001
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Q1_1 1.709 0.092 18.650 0.000 1.709 0.828
.Q1_2 0.823 0.062 13.282 0.000 0.823 0.522
.Q1_3 0.846 0.068 12.457 0.000 0.846 0.491
.Q1_4 1.612 0.091 17.623 0.000 1.612 0.738
f_A 1.000 1.000 1.000
Group 2 [2]:
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_A =~
Q1_1 (.p1.) 0.596 0.038 15.684 0.000 0.552 0.405
Q1_2 (.p2.) 0.869 0.039 22.169 0.000 0.804 0.732
Q1_3 (.p3.) 0.937 0.042 22.576 0.000 0.867 0.675
Q1_4 (.p4.) 0.756 0.041 18.308 0.000 0.700 0.478
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Q1_1 4.748 0.034 140.596 0.000 4.748 3.482
.Q1_2 4.953 0.027 182.141 0.000 4.953 4.511
.Q1_3 4.728 0.032 148.704 0.000 4.728 3.683
.Q1_4 4.818 0.036 132.793 0.000 4.818 3.289
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Q1_1 1.555 0.059 26.460 0.000 1.555 0.836
.Q1_2 0.559 0.038 14.861 0.000 0.559 0.464
.Q1_3 0.896 0.049 18.158 0.000 0.896 0.544
.Q1_4 1.656 0.065 25.361 0.000 1.656 0.772
f_A 0.856 0.075 11.434 0.000 1.000 1.000因子負荷のところに(.p1.)などといったものが表示されるようになりました。 lavaanでは,各パラメータに名前をつけられる機能があり,複数のパラメータに同じ名前をつけると等値制約をかけることができます(他の使い方は後述)。 そしてgroup.equalでパラメータの種類の指定をすると,その種類のすべてのパラメータに自動的に名前をつけることで,等値制約をかけているのです。 実際にGroup 1 [1]:とGroup 2 [2]:のそれぞれ対応する因子負荷には同じ名前がついているため,等値制約が置かれたことがわかります。
またIntercepts:欄には各観測変数の切片(=グループ平均)が表示されています。 これを見る限りではGroup 2 [2]:,つまり女性の方が平均点が高そうですが,まだ切片には等値制約を置いていないため,先ほど説明した理由よりこれが「因子得点の差」なのか「それ以外の要因の差」なのかはまだわかりません。
そしてもう一点。Group 2 [2]:の因子の分散(f_A)の値が1では無くなっています。 一方Group 1 [1]:のほうでは相変わらず因子の分散は1に固定されています, これは,因子負荷に等値制約を置いたことで,共通因子のスケールはGroup 1 [1]:側で決まり,Group 2 [2]:側では制約を置く必要がなくなったためです。 その結果,因子負荷のStd.lv列は「全ての潜在変数の分散を1にした」時の推定値なので,グループ間で値が変わってしまいます。 せっかく等値制約を置いたのに,これでは多少違和感がありますが,そういうものなのであまり気にしないでください。 実際に弱測定不変モデルの結果を報告する際には,たぶん因子負荷はEstimate列の値を載せて,各グループの因子得点の分散を記入することが多いと思います。
続いて,弱測定不変モデルと配置不変モデルの間で適合度が著しく悪化していないかを検証します。 比較の方法は セクション 7.6.5 と同じです。 多母集団モデルでは,各パラメータをグループごとに異なるものとしてそれぞれ自由に推定していました。 ここに等値制約を置くということは,自由に推定できるパラメータの数が減少していることを意味するので,それだけ適合度は悪くなるはずです。 モデル修正におけるパスの削除が「そのパスの係数を0に固定する」だとすると,多母集団モデルにおける等値制約は例えば「因子負荷\(b_i^{(\mathrm{F})}\)の値を\(b_i^{(\mathrm{M})}\)に固定する」としているようなもので,やっていることは同じなわけですね。
################### Nested Model Comparison #########################
Chi-Squared Difference Test
Df AIC BIC Chisq Chisq diff RMSEA Df diff Pr(>Chisq)
result_base 4 31636 31775 34.458
result_weak 7 31631 31753 35.925 1.4678 0 3 0.6897
####################### Model Fit Indices ###########################
chisq df pvalue rmsea cfi tli srmr aic
result_base 34.458† 4 .000 .079 .979 .936 .022† 31635.698
result_weak 35.926 7 .000 .058† .980† .965† .023 31631.166†
bic
result_base 31774.813
result_weak 31752.891†
################## Differences in Fit Indices #######################
df rmsea cfi tli srmr aic bic
result_weak - result_base 3 -0.021 0.001 0.029 0.001 -4.532 -21.922今回の等値制約では,4つの項目の因子負荷にそれぞれ等値制約を置いたため,パラメータが4つ減少しています。 一方で,先程説明したようにGroup 2 [2]:の因子の分散が自由推定可能になったことでパラメータが実は1つ増えており,弱測定不変モデルでは差し引き3つのパラメータが減少しています。 これが自由度Dfの違いに表れているのです。
結果を見ると,どうやら等値制約による当てはまりの悪化よりもパラメータを減らした(倹約度の向上)効果の方が大きいらしく,RMSEAやCFIは改善しました。 尤度比検定も有意ではなかったということで,弱測定不変性が確認されたと言って良いでしょう。
続いて,強測定不変モデル(因子負荷+切片)の検討に移ります。
lavaan 0.6-20 ended normally after 37 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 26
Number of equality constraints 8
Number of observations per group:
1 802
2 1630
Model Test User Model:
Test statistic 48.938
Degrees of freedom 10
P-value (Chi-square) 0.000
Test statistic for each group:
1 18.205
2 30.733
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Group 1 [1]:
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_A =~
Q1_1 (.p1.) 0.626 0.037 16.693 0.000 0.626 0.432
Q1_2 (.p2.) 0.882 0.039 22.885 0.000 0.882 0.701
Q1_3 (.p3.) 0.910 0.040 22.835 0.000 0.910 0.696
Q1_4 (.p4.) 0.752 0.040 18.705 0.000 0.752 0.509
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Q1_1 (.10.) 4.385 0.037 117.490 0.000 4.385 3.025
.Q1_2 (.11.) 4.504 0.040 112.782 0.000 4.504 3.582
.Q1_3 (.12.) 4.296 0.042 103.377 0.000 4.296 3.285
.Q1_4 (.13.) 4.437 0.041 108.640 0.000 4.437 3.004
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Q1_1 1.710 0.092 18.510 0.000 1.710 0.814
.Q1_2 0.804 0.062 13.057 0.000 0.804 0.508
.Q1_3 0.883 0.066 13.277 0.000 0.883 0.516
.Q1_4 1.616 0.092 17.663 0.000 1.616 0.741
f_A 1.000 1.000 1.000
Group 2 [2]:
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_A =~
Q1_1 (.p1.) 0.626 0.037 16.693 0.000 0.579 0.422
Q1_2 (.p2.) 0.882 0.039 22.885 0.000 0.816 0.743
Q1_3 (.p3.) 0.910 0.040 22.835 0.000 0.842 0.659
Q1_4 (.p4.) 0.752 0.040 18.705 0.000 0.696 0.475
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Q1_1 (.10.) 4.385 0.037 117.490 0.000 4.385 3.198
.Q1_2 (.11.) 4.504 0.040 112.782 0.000 4.504 4.099
.Q1_3 (.12.) 4.296 0.042 103.377 0.000 4.296 3.362
.Q1_4 (.13.) 4.437 0.041 108.640 0.000 4.437 3.028
f_A 0.504 0.053 9.503 0.000 0.545 0.545
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Q1_1 1.545 0.059 26.271 0.000 1.545 0.822
.Q1_2 0.541 0.037 14.646 0.000 0.541 0.448
.Q1_3 0.924 0.048 19.413 0.000 0.924 0.566
.Q1_4 1.663 0.065 25.474 0.000 1.663 0.774
f_A 0.856 0.075 11.413 0.000 1.000 1.000Group 2 [2]:のf_AのIntercepts:の値がゼロではなくなりました。 切片まで固定したことによって,因子得点の平均値が自由推定になり,比較可能になった状態です。 推定値が0.504ということは,女性の方が各観測変数のグループ平均が高かったのは確かに因子得点が平均的に高いためだ,といえそうです。 一方で,もしも適合度がひどく悪化していたら「切片がグループ間で同じというのはおかしい」ということになり,観測変数のグループ間の差は,むしろ切片項に起因するものだと言えそうです。
################### Nested Model Comparison #########################
Chi-Squared Difference Test
Df AIC BIC Chisq Chisq diff RMSEA Df diff Pr(>Chisq)
result_base 4 31636 31775 34.458
result_weak 7 31631 31753 35.925 1.4678 0.000000 3 0.68973
result_strong 10 31638 31743 48.938 13.0123 0.052389 3 0.00461
result_base
result_weak
result_strong **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
####################### Model Fit Indices ###########################
chisq df pvalue rmsea cfi tli srmr aic
result_base 34.458† 4 .000 .079 .979 .936 .022† 31635.698
result_weak 35.926 7 .000 .058 .980† .965 .023 31631.166†
result_strong 48.938 10 .000 .057† .973 .967† .030 31638.178
bic
result_base 31774.813
result_weak 31752.891
result_strong 31742.514†
################## Differences in Fit Indices #######################
df rmsea cfi tli srmr aic bic
result_weak - result_base 3 -0.021 0.001 0.029 0.001 -4.532 -21.922
result_strong - result_weak 3 -0.002 -0.007 0.002 0.006 7.012 -10.377尤度比検定は有意になった(=当てはまりが有意に悪くなった)のですが,適合度指標はさほど悪化していません。 というかRMSEAやTLIは更に改善しました。 尤度比検定はサンプルサイズが多いとすぐ有意になってしまうこともありますし,BICも強測定不変モデルを支持しているため,ここは強測定不変性が認められたと結論付けて先に進んでみましょう。
あとはどこまで測定不変性が認められるかを試すだけです。 とりあえず一気に残りの全てのモデルを推定してみます。
# 厳密な測定不変モデル
# 独自因子の分散共分散を制約に追加
# 独自因子の共分散を追加している場合は"residual.covariances"も入れる
result_strict <- cfa(model, data = dat, group = "gender", std.lv = TRUE, group.equal = c("loadings", "intercepts", "residuals"))
# (ほぼ完全な測定不変モデル)
# 共通因子の分散共分散を制約に追加
# 2因子以上の場合は"lv.covariances"も入れる
result_almost <- cfa(model, data = dat, group = "gender", std.lv = TRUE, group.equal = c("loadings", "intercepts", "residuals", "lv.variances"))
# (完全な測定不変モデル)
# 因子得点の平均を制約に追加
result_complete <- cfa(model, data = dat, group = "gender", std.lv = TRUE, group.equal = c("loadings", "intercepts", "residuals", "lv.variances", "means"))そして全部一気に適合度を比較してみます23。
################### Nested Model Comparison #########################
Chi-Squared Difference Test
Df AIC BIC Chisq Chisq diff RMSEA Df diff
result_base 4 31636 31775 34.458
result_weak 7 31631 31753 35.925 1.468 0.000000 3
result_strong 10 31638 31743 48.938 13.012 0.052389 3
result_strict 14 31652 31733 70.463 21.526 0.060026 4
result_almost 15 31657 31732 77.395 6.931 0.069841 1
result_complete 16 31760 31830 183.159 105.765 0.293522 1
Pr(>Chisq)
result_base
result_weak 0.6897314
result_strong 0.0046101 **
result_strict 0.0002491 ***
result_almost 0.0084694 **
result_complete < 2.2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
####################### Model Fit Indices ###########################
chisq df pvalue rmsea cfi tli srmr aic
result_base 34.458† 4 .000 .079 .979 .936 .022† 31635.698
result_weak 35.926 7 .000 .058 .980† .965 .023 31631.166†
result_strong 48.938 10 .000 .057† .973 .967† .030 31638.178
result_strict 70.463 14 .000 .058 .960 .966 .036 31651.703
result_almost 77.395 15 .000 .058 .956 .965 .048 31656.635
result_complete 183.159 16 .000 .093 .883 .912 .094 31760.399
bic
result_base 31774.813
result_weak 31752.891
result_strong 31742.514
result_strict 31732.854
result_almost 31731.989†
result_complete 31829.957
################## Differences in Fit Indices #######################
df rmsea cfi tli srmr aic
result_weak - result_base 3 -0.021 0.001 0.029 0.001 -4.532
result_strong - result_weak 3 -0.002 -0.007 0.002 0.006 7.012
result_strict - result_strong 4 0.001 -0.012 -0.001 0.007 13.526
result_almost - result_strict 1 0.001 -0.004 -0.001 0.011 4.931
result_complete - result_almost 1 0.034 -0.074 -0.053 0.046 103.765
bic
result_weak - result_base -21.922
result_strong - result_weak -10.377
result_strict - result_strong -9.660
result_almost - result_strict -0.865
result_complete - result_almost 97.968この結果を踏まえてどこまでの測定不変性を認めるかについては諸説ありそうです。 基本的には適合度指標が許容範囲内にある中で最も制約の強いモデルを選べば良いのではないか,と思いますが,人によって許容範囲内であっても前のモデルから適合度指標が著しく低下している場合にはアウトとする人もいます。
7.9.3 (おまけ)部分的な測定不変性
測定不変性がどこまで満たされるかをもっと厳密に検証しようとすると,ギリギリ許容できるレベルはきっと上で見たいくつかのモデルの間にあるでしょう。 例えば弱測定不変モデルの適合度は許容範囲だが強測定不変モデルまでいくと許容範囲から外れてしまう場合,置くことのできる等値制約は「全ての因子負荷+一部の切片」ということになる可能性が高いです。
ここからは,そのような部分的な測定不変性をlavaanで推定する方法を紹介していきます。 ここでは,仮に「弱測定不変までは認められるが強測定不変性は認められなかった」として,その間の部分的な強測定不変性を検証していきます。
考え方としては,許容されなかったモデルをベースに「どこの等値制約を外すと良さそうか」を見ていくことになります。 そのために有用な関数がlavTestScore()です24。
$test
total score test:
test X2 df p.value
1 score 14.128 8 0.078
$uni
univariate score tests:
lhs op rhs X2 df p.value
1 .p1. == .p15. 2.795 1 0.095
2 .p2. == .p16. 0.040 1 0.842
3 .p3. == .p17. 1.865 1 0.172
4 .p4. == .p18. 0.008 1 0.930
5 .p10. == .p24. 9.348 1 0.002
6 .p11. == .p25. 0.303 1 0.582
7 .p12. == .p26. 6.396 1 0.011
8 .p13. == .p27. 0.011 1 0.917ここで表示されているのはスコア検定(またの名をラグランジュ乗数検定)と呼ばれるものです。 compareFit()関数で出てくる検定(尤度比検定)は,複数のネストされたモデルについて,「制約のないモデル」を基準として,(a)グループ間で等値制約を置く,(b)矢印を消す(あるパラメータの値を0に制約する)など「制約を増やしたときに,増やした制約の数の割に尤度が低下していないか」を確かめるものでした。
スコア検定はこれとは反対に,「制約のあるモデル」を基準として,「制約を減らしたときに,減らした制約の数に合った尤度の改善が見られるか」を確かめるものです。 帰無仮説自体は尤度比検定のときと同じで「2つのモデルの尤度(厳密には最尤推定値)が同じであるか」なので,スコア検定が有意だった場合には「制約を減らしたほうが良さそう」と判断できるわけです。
一番上に出ている$testは,モデル全体での検定の結果です。 今回は全ての因子負荷と切片に等値制約が置かれた強測定不変モデル(result_strong)をもとに検定しているため「強測定不変モデルと配置不変モデルの比較」を直接していることになります(その意味では弱測定不変モデルのとき以外は見なくても良さそう?)。
次に出ている$uniは,パス単位で等値制約を外したときの検定です。 結果を見るのがやや大変ですが,lhsにかかれている名前はsummary(result_strong)の出力にあったパラメータ名です(rhsは等値制約を外したときにグループ2のそのパラメータにつけられるはずの別名)。 したがって,上の4つ(.p1.から.p4)が各因子負荷を,下の4つ(.p10.から.p13)が各切片を意味しています。 今回は強測定不変モデルから制約を緩めようとしているので,特に下の4つに注目してみると,.p10.つまりQ1_1に対する切片のところが\(\chi^2\)値(X2)が最大となっています。 ここから,「切片の等値制約を一つだけ外すとしたらQ1_1を外すと良い」ということが言えるわけです。
これが分かったところで,実際に部分的に等値制約を外したモデルで推定を行ってみましょう。 ここで使用するのがgroup.partialという引数です。
lavaan 0.6-20 ended normally after 43 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 26
Number of equality constraints 7
Number of observations per group:
1 802
2 1630
Model Test User Model:
Test statistic 39.596
Degrees of freedom 9
P-value (Chi-square) 0.000
Test statistic for each group:
1 11.227
2 28.369
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Group 1 [1]:
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_A =~
Q1_1 (.p1.) 0.599 0.038 15.732 0.000 0.599 0.417
Q1_2 (.p2.) 0.884 0.039 22.808 0.000 0.884 0.701
Q1_3 (.p3.) 0.918 0.040 22.859 0.000 0.918 0.701
Q1_4 (.p4.) 0.757 0.040 18.746 0.000 0.757 0.512
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Q1_1 4.278 0.051 84.310 0.000 4.278 2.977
.Q1_2 (.11.) 4.522 0.040 112.334 0.000 4.522 3.589
.Q1_3 (.12.) 4.310 0.042 102.718 0.000 4.310 3.292
.Q1_4 (.13.) 4.450 0.041 108.457 0.000 4.450 3.009
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Q1_1 1.706 0.092 18.629 0.000 1.706 0.826
.Q1_2 0.806 0.062 13.041 0.000 0.806 0.508
.Q1_3 0.872 0.067 13.063 0.000 0.872 0.508
.Q1_4 1.613 0.091 17.633 0.000 1.613 0.738
f_A 1.000 1.000 1.000
Group 2 [2]:
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_A =~
Q1_1 (.p1.) 0.599 0.038 15.732 0.000 0.554 0.406
Q1_2 (.p2.) 0.884 0.039 22.808 0.000 0.817 0.743
Q1_3 (.p3.) 0.918 0.040 22.859 0.000 0.849 0.663
Q1_4 (.p4.) 0.757 0.040 18.746 0.000 0.700 0.478
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Q1_1 4.463 0.044 100.948 0.000 4.463 3.273
.Q1_2 (.11.) 4.522 0.040 112.334 0.000 4.522 4.110
.Q1_3 (.12.) 4.310 0.042 102.718 0.000 4.310 3.368
.Q1_4 (.13.) 4.450 0.041 108.457 0.000 4.450 3.034
f_A 0.476 0.053 8.927 0.000 0.515 0.515
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Q1_1 1.552 0.059 26.450 0.000 1.552 0.835
.Q1_2 0.543 0.037 14.562 0.000 0.543 0.448
.Q1_3 0.917 0.048 19.119 0.000 0.917 0.560
.Q1_4 1.660 0.065 25.427 0.000 1.660 0.772
f_A 0.855 0.075 11.427 0.000 1.000 1.000結果を見ると,確かにIntercepts:のQ1_1のところの等値制約が外れています。 あとは適合度の比較をするだけです。
################### Nested Model Comparison #########################
Chi-Squared Difference Test
Df AIC BIC Chisq Chisq diff RMSEA Df diff
result_weak 7 31631 31753 35.925
result_strong_p 9 31631 31741 39.596 3.6704 0.026208 2
result_strong 10 31638 31743 48.938 9.3419 0.082826 1
Pr(>Chisq)
result_weak
result_strong_p 0.15958
result_strong 0.00224 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
####################### Model Fit Indices ###########################
chisq df pvalue rmsea cfi tli srmr aic
result_weak 35.926† 7 .000 .058 .980† .965 .023† 31631.166
result_strong_p 39.596 9 .000 .053† .979 .971† .025 31630.836†
result_strong 48.938 10 .000 .057 .973 .967 .030 31638.178
bic
result_weak 31752.891
result_strong_p 31740.969†
result_strong 31742.514
################## Differences in Fit Indices #######################
df rmsea cfi tli srmr aic
result_strong_p - result_weak 2 -0.005 -0.001 0.006 0.001 -0.330
result_strong - result_strong_p 1 0.004 -0.006 -0.004 0.005 7.342
bic
result_strong_p - result_weak -11.923
result_strong - result_strong_p 1.545結果を見ると,部分的な強測定不変モデル(result_strong_p)は,弱測定不変モデル(result_weak)と比べても尤度の低下が大きくなく,またRMSEAやAIC, BICなどは改善しており,何なら強測定不変モデルよりも良い値になっています。
…という感じで,測定不変性を細かいところまで見ていくことも可能です。 因子分析で言えば,特定の項目だけ切片が異なるというのは,もしかしたらその項目にDIF的な要素があったことを示しているのかもしれません。 このあたりも掘り下げることができれば面白い示唆が得られるかもしれないので,余裕があればいろいろ試してみると良いでしょう。
7.10 lavaanの記法
知っていると役に立つ日が来るかもしれない,lavaanのより高度な記法について少しだけ紹介します。
7.10.1 パラメータの制約
尺度を作成する際には,探索的因子分析の結果2項目だけの因子が誕生してしまうことがあります。 ですが2項目だけの因子は,モデル的には単体では結構危うい存在です。 実際に,2項目1因子のみの因子分析モデルを考えてみましょう。 この場合,推定するパラメータは因子負荷と独自因子の分散がそれぞれ2つずつで計4つです。 その一方で,データの分散共分散は3つしかありません。 つまりそのままでは推定に失敗する,ということです25。
試しに2項目1因子の(うまくいかない)モデルをやってみましょう。
Warning: lavaan->lav_model_vcov():
Could not compute standard errors! The information matrix could not
be inverted. This may be a symptom that the model is not identified.lavaan 0.6-20 ended normally after 9 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 4
Number of observations 2432
Model Test User Model:
Test statistic NA
Degrees of freedom -1
P-value (Unknown) NA
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_A =~
Q1_1 1.010 NA 1.010 0.719
Q1_2 0.575 NA 0.575 0.491
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Q1_1 0.954 NA 0.954 0.483
.Q1_2 1.044 NA 1.044 0.759
f_A 1.000 1.000 1.000出力を見るとDegrees of freedomが-1になっており,検定も行われていません。 一応因子負荷は出ているのですが,実際のところこれが正しいという保証は全くありません。 本当はこのような場合には,項目数を増やしたり他の項目と合わせて因子構造を再検討するのが重要になるのですが,もしもどうしてもこの2項目だけで行かなければならない場合には,とりあえず2項目の因子負荷に等値制約をかけることで推定するパラメータ数を減らす事ができます。
モデルの修正のところで,右辺の変数名の前に0*をかけることで共分散をゼロに固定する方法を紹介しました。 それと同じように,ここでは右辺の変数名の前に共通のb1をかけています。
lavaan 0.6-20 ended normally after 11 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 4
Number of equality constraints 1
Number of observations 2432
Model Test User Model:
Test statistic 0.000
Degrees of freedom 0
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_A =~
Q1_1 (b1) 0.762 0.023 32.813 0.000 0.762 0.543
Q1_2 (b1) 0.762 0.023 32.813 0.000 0.762 0.650
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Q1_1 1.394 0.051 27.466 0.000 1.394 0.706
.Q1_2 0.793 0.039 20.520 0.000 0.793 0.577
f_A 1.000 1.000 1.000結果を見ると,因子負荷の欄に測定不変性の検証の時と同じように(b1)という表記が追加されています。 パラメータ数を減らしたことによって,Degrees of freedomが0(つまり飽和モデル)になり,晴れてパラメータの検定が行われるようになりました。
尺度得点として,因子得点ではなく和得点を使うケースが多いことはすでに説明したとおりです。 このような場合でも,尺度作成論文では通常「1項目が1因子にのみ負荷している状態(完全な単純構造)」でCFAを行い,モデル適合度を確認しています。 ですがよく考えると,尺度得点が和得点であるならば,CFAを行う際に因子負荷には等値制約をかけたほうがよいのではないかという気がしています。
因子負荷の大きさは,その項目が因子得点の推定に与える影響の強さを表しています。 言い換えると,因子負荷はその項目の重みという見方ができるということです。 そう考えると,等値制約を置かないCFAによるモデル適合度の検証は「重み付け得点を使用した場合の適合度」であり,もしも項目の重みが極端に異なる場合は,重み付けない単純な和得点では著しく適合度が悪化する可能性があります。
したがって,「和得点でのモデル適合度」を検証するために,因子ごとに全ての因子負荷に等値制約をおいた状態でのモデル適合度を評価すべきではないか,という気がするのですが実際にそのようにしている研究は見たことが無い気が…と思っていたらこんな論文がありました。→ McNeish & Wolf (2020)
等値制約は他にも,多母集団同時分析で特定の回帰係数が同じかどうかを評価する際や,複数時点で同一のモデルを測定する場合に共通のパスが同じ値かを検討する際にも使ったりします。 多母集団同時分析に関して,例えば 図 7.17 の回帰分析モデルを性別ごとに行い,「ageがQ1_Aにおよぼす影響」が男女間で同じかを検討したい場合には,以下のようにして,等値制約あり/なしのモデルを比較すると良いですね。
################### Nested Model Comparison #########################
Chi-Squared Difference Test
Df AIC BIC Chisq Chisq diff RMSEA Df diff Pr(>Chisq)
result_base 0 12810 12856 0.0000
result_const 1 12810 12850 2.0076 2.0076 0.030048 1 0.1565
####################### Model Fit Indices ###########################
chisq df pvalue rmsea cfi tli srmr aic
result_base .000† NA .000† 1.000† 1.000† .000† 12809.872†
result_const 2.008 1 .157 .030 .978 .911 .009 12809.880
bic
result_base 12855.557
result_const 12849.854†
################## Differences in Fit Indices #######################
df rmsea cfi tli srmr aic bic
result_const - result_base 1 0.03 -0.022 -0.089 0.009 0.008 -5.703このように掛け算する時にgroupの数と同じ長さのc()を与えると,グループの順にそれぞれパラメータに名前を付けることができます。 もちろんc(0.5, 0.6)*というように直接数字を入力することによって,グループごとに異なる値に固定することもできます。
7.10.2 等式・不等式制約
図 7.19 のように,各因子の2番目の項目を逆の因子に入れてしまった因子分析モデルを考えます。
このモデルを推定すると,(設定をミスっているので)推定値が変なことになります。
Warning: lavaan->lav_object_post_check():
covariance matrix of latent variables is not positive definite ; use
lavInspect(fit, "cov.lv") to investigate.するとなにやらWarningが出てきました。 どうやらメッセージを読む限りは「潜在変数の共分散行列が正定値(positive definite)ではない」ということですが,つまりどういうことでしょうか。
lavaan 0.6-20 ended normally after 33 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 13
Number of observations 2432
Model Test User Model:
Test statistic 844.850
Degrees of freedom 8
P-value (Chi-square) 0.000
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_A =~
Q1_1 0.500 0.033 15.207 0.000 0.500 0.356
Q1_7 0.407 0.030 13.355 0.000 0.407 0.309
Q1_3 0.726 0.034 21.515 0.000 0.726 0.556
f_E =~
Q1_6 0.318 0.029 11.027 0.000 0.318 0.258
Q1_2 0.753 0.034 22.179 0.000 0.753 0.642
Q1_8 0.372 0.030 12.325 0.000 0.372 0.289
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_A ~~
f_E 1.290 0.057 22.693 0.000 1.290 1.290
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Q1_1 1.725 0.053 32.801 0.000 1.725 0.874
.Q1_7 1.566 0.047 33.520 0.000 1.566 0.904
.Q1_3 1.177 0.048 24.574 0.000 1.177 0.691
.Q1_6 1.415 0.042 33.927 0.000 1.415 0.933
.Q1_2 0.808 0.046 17.491 0.000 0.808 0.588
.Q1_8 1.519 0.045 33.623 0.000 1.519 0.916
f_A 1.000 1.000 1.000
f_E 1.000 1.000 1.000Covariances:の推定値(35行目)が1.290になっています。 この値は,2つの因子f_Aとf_Eの相関係数を表しているはずなので1を超えるのは明らかにおかしな話です。 このように,モデルの設定をめちゃめちゃ失敗すると不適解が発生してしまいます。 不適解が生じた場合には,基本的にはモデルに誤設定がある(あまりに変なパスを引いてしまっている or 絶対に必要なパスを引いていなかったり,変な変数が入っていたり)可能性が高いので,まずはそれを修正するべきです。
ただ場合によってはモデルの設定は問題ないという自負があるにも関わらず不適解が生じることがあります。 よくあるのはデータが悪い状況です。 SEMでは,データにおいて観測された分散共分散をもとにして,モデル上の分散共分散を推定していきます。 したがって,データが酷い(サンプルサイズが小さい・欠測値が多すぎる・適当な回答が見られる)ときには,モデルが正しくてもうまく推定できないことがあります26。 セクション 3.2 において,事前に適当な回答をしているデータを除外する方法を紹介したのはこのような事態を回避するためでもあったのです。
そして特にモデルが複雑な場合やデータがひどい場合には,独自因子の分散がマイナスになったり相関係数が1を超えるなどの事態(Heywood case)が起こることがあります。 基本的には不適解はそのまま報告してはいけないのですが,
- どう考えてもモデルは正しいし,
- データには問題ない(と思っている)し,
- 不適解の部分以外はいい感じの推定値だし,
- 不適解といってもギリギリアウト(独自因子の分散が-0.005とか)
という感じで,自分は悪くないと言い切れる自信がある状況であれば,多少の不適解には目をつぶって27不等式制約をかけてとりあえず結果を報告することがあります。 そういう場合には,パラメータに上限・下限を定めて推定するという方法をとります。
lavaan 0.6-20 ended normally after 29 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 13
Row rank of the constraints matrix 2
Number of observations 2432
Model Test User Model:
Test statistic 862.410
Degrees of freedom 8
P-value (Chi-square) 0.000
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_A =~
Q1_1 0.585 0.033 17.760 0.000 0.585 0.416
Q1_7 0.315 0.031 10.041 0.000 0.315 0.239
Q1_3 0.843 0.032 26.209 0.000 0.843 0.645
f_E =~
Q1_6 0.253 0.029 8.579 0.000 0.253 0.205
Q1_2 0.884 0.030 29.289 0.000 0.884 0.754
Q1_8 0.347 0.031 11.336 0.000 0.347 0.270
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_A ~~
f_E (cor) 1.000 1.000 1.000
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Q1_1 (vr_1) 1.633 0.052 31.646 0.000 1.633 0.827
.Q1_7 1.632 0.048 33.979 0.000 1.632 0.943
.Q1_3 0.995 0.047 21.346 0.000 0.995 0.584
.Q1_6 1.453 0.042 34.230 0.000 1.453 0.958
.Q1_2 0.594 0.043 13.723 0.000 0.594 0.432
.Q1_8 1.537 0.046 33.715 0.000 1.537 0.927
f_A 1.000 1.000 1.000
f_E 1.000 1.000 1.000ということで,Warningも出ずに無事推定できました。 ただ,この方法はあくまでも対処療法です。まずはモデルの誤設定の可能性を完全に消し去るのが第一です。
不等式制約と同じように,等式制約や四則演算による制約を置くことも可能です。 例えば(意味があるかはともかく)「項目1の因子負荷」が「項目2と項目3の因子負荷の平均」よりも大きいということが仮説から言えるとしたら,次のような書き方が出来ます。
7.10.3 推定しないパラメータの定義(媒介分析)
SEMでよくあるのが,ある変数が別の変数に及ぼす効果を「直接的な効果(直接効果)」と「別の変数を介して及ぼす効果(間接効果)」に分解して考えるモデルです。 図 7.20 では,学歴に性別が及ぼす効果について,「性別が勤勉性(Q1_C)を介して学歴に影響している」という間接効果を考えています。
このように,ある変数間の関係に第3の変数を考える分析のことを媒介分析(mediation analysis)と呼びます。 Baron & Kenny (1986) の枠組みでは,genderからeducationに対するQ1_Cの媒介効果を確認するためには
Q1_Cをモデルから消したときにはgenderからeducationへの単回帰が有意である- その上で
genderからQ1_Cへの単回帰もQ1_Cからageへの単回帰も有意になる Q1_Cをモデルに含めた場合には,genderからeducationへの直接効果が有意ではなくなる
ことを示せば良いとしています。 理想的には3点目に関してgenderからeducationへの直接効果が完全にゼロになってくれれば,「genderはQ1_Cを通してのみeducationに影響を与える」ということがハッキリ言えるわけですが,実際にはなかなかそうもいきません。 とりあえずgenderからeducationへの直接効果が有意に減少してくれれば万々歳です。
図 7.20 のモデルでは,genderからeducationへの経路は2つあります。 こうしたケースでは2変数の共分散は「全ての経路のパス係数の積の和」となりました。 媒介分析でも同じように,直接効果が\(c\),間接効果が\(ab\)と表されるならば,これらを合わせた\(ab+c\)がgenderからeducationへの総合効果となります。 先程の1点目は,言い換えると「genderからeducationへの総合効果が有意である」ということです。
したがって,先程の Baron & Kenny (1986) の枠組みをSEMのパラメータで表すと
- \(H_1:ab+c\neq0\)
- \(H_2:a\neq0\)
- \(H_3:b\neq0\)
- \(H_4:ab\neq0\)
を全て示すことができれば,Q1_Cによる媒介効果を認めることができるわけです28。
それではlavaanで媒介分析を行ってみましょう。
ここでのポイントは":="という記号です。これをを使うと,ラベル付けしたパラメータの推定値に基づいて計算をしてくれます。 上の例では,まず 図 7.20 に沿って各回帰係数にa,b,cというラベルを付けています。 そして"ab := a*b"と書くことで,「a*bをabと定義します」という意味になります。 ":="によって記述した場合,abというパラメータを推定するということはありません。ただ単に推定されたaとbの値をもとに,事後的にabを計算して出力してくれるようになります。 一方,もしもab = a*bと書いてしまうと,abは(a*bとの等値制約が置かれた)パラメータとして推定されてしまいます。
lavaan 0.6-20 ended normally after 7 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 5
Used Total
Number of observations 2232 2432
Model Test User Model:
Test statistic 0.000
Degrees of freedom 0
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Regressions:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
education ~
Q1_C (b) 0.006 0.005 1.187 0.235 0.006 0.025
gender (c) 0.007 0.050 0.134 0.893 0.007 0.003
Q1_C ~
gender (a) 0.822 0.213 3.852 0.000 0.822 0.081
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.education 1.235 0.037 33.407 0.000 1.235 0.999
.Q1_C 22.423 0.671 33.407 0.000 22.423 0.993
Defined Parameters:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
ab 0.005 0.004 1.134 0.257 0.005 0.002
total 0.012 0.050 0.232 0.817 0.012 0.005Defined Parameters:という箇所が増えました。 定義されたパラメータについても,自由推定されたパラメータと同じように仮説検定まで行ってくれます。 ということで,これを使えば先程の仮説群をまとめて検証することが出来ます。 ただ今回の場合では,そもそもtotalの推定値から,\(H_1:ab+c\neq0\)が有意ではないことが分かるのでおしまいです29。
7.11 同値モデル
突然ですが,同じ4つの観測変数について, 図 7.21 に2つの異なるモデルを考えました。 上は「genderがeducationに及ぼす影響」を考えるモデルです。 これに対して下のモデルでは矢印の向きを全てひっくり返して「educationがgenderに及ぼす影響」を推定するモデルになっています。
普通に考えたら,少なくとも「学歴によって性別が影響を受ける」よりは「性別によって学歴が影響を受ける」上のモデルのほうが自然な気がしますが,とりあえずこれらのモデルを分析してみましょう。
実はこの2つのモデルでは,RMSEA, CFI, TLI, SRMRといった適合度指標は全て完全に同じ値になります30。 ダガー(†)がついているのは,数値計算上の細かいズレのためであり,これも小数点第9位くらいでやっと差が出る程度の違いしかありません。 適合度指標が完全に一致しているということは,モデル上の共分散行列(\(\symbf{\Sigma}\))に関しても全く同じ値になっているということなので,これらの2つのモデルは統計的には優劣をつけることが出来ません。 こうしたモデルのことを同値モデル(equivalent model)と呼びます。
基本的には,回帰を含むSEMのモデルには多少なりとも同値モデルが存在しており,可能であればこうした同値モデルに関しても議論をしておくべきだという意見もあります(Kang & Ahn, 2021) 31。 多くの場合,同値モデルは 図 7.21 のように,どこかしらの矢印の向きを反対にしたモデルです。 一部の人はSEM(あるいは回帰分析)の矢印を「因果関係」かのように扱ってしまいますが,これは誤った考え方です。 統計的にはデータに対する当てはまり(=モデルの「良さ」)が完全に同じモデルがあるということは,分析上は矢印の向きはどちらでも良いといえます。 これは回帰分析の\(x\)と\(y\)は入れ替えても問題ないのと同じです。 したがって,特にSEMを実施する際には,分析者は統計以外の側面から,つまり先行研究などを踏まえてなるべく理論的に矢印の向きを指定する必要があります。 「同値モデルに関しても議論をしておくべき」というのは「なぜ矢印の向きが逆ではいけないのか」をきちんと説明しておく必要があるということです。
7.12 \(ω_h\)を求める
セクション 6.12 で紹介した\(\omega\)係数のお話の続きです。 今回は,分析者が事前に設定した因子構造における\(\omega_h\)を求める方法を紹介します。
7.12.1 双因子モデル
図 7.22 の10項目2因子のモデルに関してやってみましょう。
まずは今までと同じようにcfa()でパラメータの推定を行います。 ただし,\(G\)因子にあたるものを用意する点に注意です。
\(\omega\)係数を算出するためにはsemTools::compRelSEM()という関数を使います32。
出てくる値は,それぞれの因子のみの\(\omega\)係数です。 したがって,gのところにある0.566という値が,\(\omega_h\)を表しています。 セクション 6.12 のなかでomega()関数で出した値(0.42)と比べるとそこそこ大きな値になっています。 これは「カテゴリカル因子分析にした」ことと「もう一方の因子に対する因子負荷を完全にゼロにした」ことが理由だと思われます。 g以外の特殊因子の値は,「G因子の影響を取り除いた\(\omega\)」という位置づけなので,使う機会は無いでしょう。 また,引数return.total = TRUEとすると,\(\omega_t\)も出してくれます。 ただ セクション 6.12 でお話したように,一つの尺度の内的一貫性に関心がある場合には\(\omega_t\)を優先的に使うことは無いと思うので,基本的にはそのままでOKです。
7.12.2 高次因子モデル
G因子の位置づけに関して,場合によっては 図 7.23 のように各特殊因子の上位にあると考えるほうが妥当なケースがあるかもしれません(総合的な学力に対する「文系」「理系」なんかはまさにそれ)。
このような場合に,全ての項目をまとめて一つの得点と考えた場合の内的一貫性は,先ほどの\(\omega_h\)とは異なる形になります。 例えば一番左の項目1について式を展開すると(因子\(f_A\)は内生変数となっているために誤差\(\symbf{\varepsilon}_A\)を追加して), \[ \begin{aligned} \symbf{y}_1 &= \symbf{f}_Ab_{1} + \symbf{\varepsilon}_1 \\ &= (\symbf{G}b_{A}^{g} + \symbf{\varepsilon}_A)b_{1} + \symbf{\varepsilon}_1 \\ &= \symbf{G}b_{A}^{g}b_{1} + \overbrace{b_{1}\symbf{\varepsilon}_A + \symbf{\varepsilon}_1}^{\mathrm{error}} \end{aligned} \tag{7.51}\] となるため,真値\(t\)に相当する部分は\(\symbf{G}b_{A}^{g}b_{1}\)となります。したがって,その係数\(b_{A}^{g}b_{1}\)を使って,高次因子モデルにおける\(\omega_{ho}\)は \[ \omega_{ho} = \frac{\left(\sum_{i=1}^{I}b_{\cdot}^{g}b_{i}\right)^2}{\sigma_{y_\mathrm{total}}^2} \tag{7.52}\] となります。\(b_{\cdot}^{g}\)は項目によって\(b_{A}^{g}\)か\(b_{C}^{g}\)になるものです。
数理的にはそういう扱いですが,lavaanで行う場合にはそれほど難しくはありません。 まずはいつも通りモデルを組みます。 (2因子だと解が求められなかったので3因子分用意しています。)
あとはsemTools::compRelSEM()に入れるだけです。
高次因子があるモデルについて計算する場合は,引数higherに高次因子の名前を入れてあげるだけです。 先ほどと同じようにgのところにある0.638という値が,\(\omega_{ho}\)を表しているわけです。 このように,semTools::compRelSEM()を利用することで,「完全な単純構造ではない場合の\(\omega\)」や「独自因子の間に相関を認めた場合の\(\omega\)」などもフレキシブルに計算可能です。
7.13 もう一つのSEM
これまでに紹介してきたSEMは,共分散構造分析という別名にも表れているように,観測変数間の共分散(相関係数)をうまく復元できるようにモデルのパラメータを推定する方法です。この共分散に基づくSEM (Covariance Based SEM: CB-SEM) に対して,主にマーケティングの分野として(とはいえ今では様々な分野で使われている),異なるSEMが独自に発展しているようです。 ということで最後に,もう一つのSEMことPLS-SEM (Partial Least Squares SEM: Wold, 1975)を簡単に紹介します。
SEMは多変量解析の手法ですが,もともと多変量解析の手法としては重回帰分析や分散分析,クラスター分析などのシンプルな手法が存在しています。20世紀にはこうした手法によって(あるいはこうした手法に当てはめられるようにRQやデータを設計することで)多変量解析の研究が行われていました。 しかしこうした手法には,(a)複雑なモデルを考えることができない,(b)潜在変数を考えることができない(すべての変数は直接観測可能だとみなす),(c)測定誤差というものを明示的に考えることができない,といった限界がありました (Haenlein & Kaplan, 2004)。 これらの問題を解決するために考案されたのが(CB-)SEMということになるようです。 そもそもSEMというものは「構造方程式モデリング」と訳される名が示すように,潜在変数を含む複雑な変数間の関係性を(連立)方程式によって表現し,そのパラメータをデータから推定する方法でした。 PLS-SEMとは,その定式化および推定の方法として,CB-SEMとは別の文脈から生まれてきたもののようです。
7.13.1 モデルの設計
したがって,PLS-SEMにおいても「構造方程式モデリング」としての基本的なコンセプトはCB-SEMと大きく変わりません。 とりあえず観測変数間の関係性をモデルに起こすところから始まります。 図 7.24 は,ホテル利用者が行う評価に及ぼす影響をイメージした仮想的なグラフィカルモデルです33。 このモデルには,以下の3つの潜在変数およびそれらを測定する計7項目の観測変数があるとします。
- 【満足度】 ホテルのサービスに対する満足度。以下の3項目によって,それぞれ7段階評価で測定される。
- スタッフの対応は良かった。(
sat_1) - ホテルは綺麗だった。(
sat_2) - 食事は美味しかった。(
sat_3)
- スタッフの対応は良かった。(
- 【価格】 (主観的な)価格。「1泊あたりの価格はどう感じましたか。(
price)」という1項目に対して「とても安かった」から「とても高かった」までの7段階評価。 - 【評価】 ホテルの評価。以下の3項目によって,それぞれ7段階評価で測定される。
- このホテルのファンになった。(
rate_1) - 機会があればまたこのホテルに泊まりたい。(
rate_2) - このホテルを他の人に薦めたい。(
rate_3)
- このホテルのファンになった。(
このような図は,CB-SEMでも見ることがあるかと思いますが,いくつか気になる点があります。
1点目は,3つの観測変数から「満足度」という潜在変数に対して矢印が刺さっている点です。 これまでのCB-SEMの説明では,矢印は必ず潜在変数から観測変数に向かって刺さっていました。つまり逆向きです。 実はPLS-SEMでは,このような逆向きの矢印もモデルに含めることができると言われています。
では,具体的にこの矢印の向きの違いは何を表しているのでしょうか。 CB-SEMで用いられてきた矢印の向きは,「複数の観測変数の共通原因としての潜在変数が存在する」ということを考えていました。 ここでは,潜在変数を測定するために「観測変数に反映された共通部分」を見出そうとします。 そういった意味で,reflective measurementと呼ばれることがあります。 図 7.24 の中では「評価」という因子はreflectiveなものとみなされています。 rate_1-3の項目を見るとわかりますが,これらの項目への回答はきっと多くの人では互いに似たものになり,それは「ホテルに高い評価をした人ほどいずれも『当てはまる』寄りの回答をするだろう」という推測が立ちます。
一方で, 図 7.24 に登場した逆向きの矢印は,「複数の観測変数の総体として潜在変数が形作られる34」と考えます。 そのため,こちらの矢印はformative measurementを表したものだと呼ばれます。 「満足度」を評価するsat_1-3の項目は,一部共通する側面はあるものの,共通の「原因」を持っていないと考えられます。 つまり,「従業員の対応は良いがあまり綺麗ではないホテル」や「ご飯は美味しいが従業員が無愛想なホテル」などが存在することは容易に想像でき,また「(全体的な)満足度」というものはこうした個別の要素を組み合わせて決まってくるはずです。 「総合的に見て満足だと感じたから,ご飯は美味しかったし従業員は良くしてくれた…気がする」というようにレビューをする人はいないでしょう。
reflectiveとformativeの違いを表した図が, 図 7.25 です。 reflective measurementでは,各観測変数が尋ねている内容(構成概念の一側面)の共通部分(積集合)が潜在変数として表れている,と考えます。 そして各観測変数(rate_1-3)は共通の原因変数(「評価」)の影響を受けているため,基本的に相関係数は高いはずです。 一方でformative measurementでは,そもそも各観測変数が高い相関を持っている必要はありません。 そして潜在変数は,観測変数の和集合として規定されている,と考えているわけです。
ここまでの話は,どちらが良いとか悪いとかの話ではなく,あくまでも潜在変数の考え方の違いの話です。 どちらの考え方も本質的にはあり得るわけですが,CB-SEMではformative measurementは表現できない,という点においてPLS-SEMを積極的に使う理由が生まれるかもしれませんね。
図 7.24 のモデルの違和感の2点目は,「価格」という潜在変数が1つの観測変数のみと,しかも矢印ではなくただの線で繋がっている点です。 このようにPLS-SEMでは,このように単一の観測変数をそのまま潜在変数として利用することができると言われています。 一方でCB-SEMでは,モデルの識別のために,各潜在変数に対して少なくとも3つの観測変数が必要でした。 PLS-SEMで単一の観測変数を潜在変数扱いにしている理由は,どうやら計算上の都合によるところが大きいです。 というのも後ほど説明しますが,PLS-SEMでは「観測変数から潜在変数の得点を推定する(測定モデル)」「潜在変数同士の関係(パス係数)を推定する(構造モデル)」という2つの計算を別々に行い,これらを交互に繰り返します。 PLS-SEMではこのうち構造モデルにおいて,観測変数と潜在変数の間のパス解析(回帰)を考えないために,観測変数を便宜的にそのまま潜在変数として扱っているような気がします。 したがって,単一観測変数から潜在変数の得点を推定するといっても結局やっていることは恒等変換にすぎません。 ちなみにCB-SEMの推定では構造モデルと測定モデルを区別せずにまとめて同時に推定しているので,このような場合はわざわざ「潜在変数に置き換える」ことはせずに,潜在変数のまま扱うことができます。
7.13.2 推定
続いてPLS-SEMのパラメータ推定のイメージを紹介します。 その前にCB-SEMにおけるパラメータ推定の基本理念をおさらいすると,CB-SEMでは「推定されたパラメータから復元された共分散行列\(\symbf{\Sigma}\)」と「データにおける観測された共分散行列\(\symbf{S}\)」のズレが最も小さくなるようにパラメータを推定していました。 これはいわば,データを最も良く説明できるパラメータの組を求める行為です。
これに対してPLS-SEMの基本理念は,内生潜在変数 (endogenous latent variable) を予測した際の分散説明率を最大化するようにパラメータを推定していきます35。 内生潜在変数とは,他の(外生)潜在変数からの矢印が刺さっている潜在変数( 図 7.24 では「評価」)です。 PLS-SEMでは,最終的に内生潜在変数を被説明変数とした(重)回帰分析における分散説明率=決定係数(\(R^2\))の値が最大になるように,以下に示した4つのステップを繰り返して推定を行います。 具体的な各ステップを見てみましょう (Henseler et al., 2012)。
ステップ1
とりあえず各潜在変数の得点を観測変数から求める( 図 7.26 )。この時点では矢印の向きによらず,すべて観測変数の重み付け和として求める。初期値は全ての重みを1とする(=単純な和得点から始める)。
ステップ2
各内生潜在変数を対応する外生潜在変数によって回帰してパス係数を求める( 図 7.27 )。普通に最小二乗法で回帰してあげれば自ずと決定係数(\(R^2\))が最大になるパス係数を求めることができる。
ステップ3
得られたパス係数を使って各内生潜在変数の値を再計算する( 図 7.28 )。ここでは,内生潜在変数の値を外生潜在変数の重み付け和として計算し,ステップ1で得られた値から置き換える。外生潜在変数の値については多分ノータッチ。
ステップ4
ステップ1で用いる潜在変数得点計算時の各観測変数の重みを以下の方法で置き換える( 図 7.29 )。
- reflective measurementの箇所は潜在変数得点と観測変数との相関係数に置き換える(mode A)。
- formative measurementの箇所は観測変数一つ一つから潜在変数への単回帰を行った回帰係数に置き換える(mode B)。
以上4つのステップを解が変わらなくなるまで繰り返すことで,最終的な推定値を得ます。 細かく見ると,PLS-SEMでは図7.26‐7.29の中の点線で囲った部分ごとに計算をしていることになります。
7.13.3 CB-SEMとPLS-SEMの使い分け
これまでに紹介してきたPLS-SEMの特徴を踏まえると,CB-SEMとの使い分けのポイントが見えてきます。 ここでは (Hair et al., 2021, Table 1.6)をもとに,使い分けのポイントをいくつか見てみましょう。
- 分析の目的が説明(観測されたデータ全体に最もよく当てはまるモデルパラメータを推定すること)よりも予測(外生潜在変数から内生潜在変数をできるだけ精度良く予測・説明すること)に関心がある場合はPLS-SEMが良い。
- formative measureな潜在変数が含まれる場合は,CB-SEMでは難しいのでPLS-SEMを使うしかない。
- サンプルサイズが小さい場合はPLS-SEMのほうが良い。というのもPLS-SEMは基本的に回帰分析の組み合わせなので,CB-SEMと比べると少ないサンプルサイズでもそれなりに安定した解が出やすい,らしい。
- 観測変数の(多変量)正規性が怪しい場合はPLS-SEMのほうが良い。というのもCB-SEMは変数の分散共分散行列をもとに推定を行うが,その方法として,多変量正規性を仮定した最尤法などが用いられるため,仮定が満たされない場合は厳しい。
PLS-SEMの利用に関するいくつかのレビュー論文によれば,PLS-SEMを使う理由として最も多く挙げられているのが「サンプルサイズが小さい」,そして「データの非正規性」「予測が目的」「モデルが複雑」などが続いているようです (e.g., Bayonne et al., 2020; Lin et al., 2020; Magno et al., 2022) 。
しかしPLS-SEMにはそれなりの反対意見もあるようで,一部の人は「PLS-SEMはくそくらえだ」という感じもあります (e.g., Rönkkö et al., 2015) 。 例えば,そもそもPLSによる推定値には一致性がないことが昔から知られており(e.g., Dijkstra, 1983; Rönkkö et al., 2016),一般的にはパス係数や相関係数を過小推定する傾向があります。 ということで,理論(研究仮説)的にPLS-SEMのほうが適切だと自信を持って言い切れるかつ場合にはPLS-SEMを使えばよいのですが,どちらを使えば良いかわからない(どちらでもいける)場合には,とりあえずCB-SEMを試してみて,よほど特殊な事情がある場合に初めてPLS-SEMの利用を考えるくらいで良いのかもしれません。
- formative measurementを行いたいんだ!
- →後述するように,CB-SEM(
lavaan)でもformative measurementができるようになりつつありますよ。
- →後述するように,CB-SEM(
- サンプルサイズが小さいから仕方ないんだ!
- CB-SEMで安定しないくらいの結果しか出せないサンプルサイズなのだとしたら,PLS-SEMでもあまり良いとは言えないのではないでしょうか(e.g., Goodhue et al., 2012)。安易にPLS-SEMに逃げるよりもサンプルサイズを増やすことを先に検討すべきだと思いますよ。
- データの正規性が怪しいのです。
- CB-SEMにも,正規性の逸脱に対して頑健なパラメータ推定法(MLRなど)は用意されていますよ。
- モデルが複雑なので,CB-SEMだと解が出ないんですよねぇ。
- 確かにPLS-SEMは何かしらの解を出してくれますが,そもそもCB-SEMで解が得られないということ自体が「モデルが不適切である」ことのシグナルである可能性もあります。PLS-SEMで出てきた解が理論的に「本当に欲しかったもの」であるかはきちんと確認する必要がありそうです。
どうやら今のところは,PLS-SEMを使う積極的な理由は「予測精度の最大化が目的である」という点くらいなようです。 ただ,その理由のためにbiasedな推定を行うことが理論的にどの程度許容されるかは分かりません……
7.13.4 PLS-SEMを実行する方法
PLS-SEMを実行するためのソフトウェアとして,SmartPLSというものがよく用いられているようです。 一応RでもPLS-SEMを行うためのパッケージとしてplssemやseminr (SEM in R)パッケージというものが作成されているので,関心がある方はそちらのパッケージを見てみてください。 ちなみに Hair et al. (2021) はseminrパッケージの使い方を紹介しているOA本です。
7.13.5 lavaanでformativeな測定
2025年9月にリリースされたバージョン0.6-20以降では,lavaanのやり方(つまりCB-SEMの枠組み)でformative measurementができるようになりました。 いよいよPLS-SEMを積極的に利用する必要性が分からなくなってきましたね。
理論的な詳細は Schamberger et al. (2025) を見ていただくとして(私もまだ十分にはチェックできていない&まだプレプリントなので),以下に示すいくつかの制約を満たす限り(バージョン0.6-20時点で)は,formative measurementを含んだCB-SEMを実行することができます。
- formativeな因子は,それぞれが少なくとも1つの「自身を構成している観測変数」以外と矢印でつながっている
- formativeな因子とreflectiveな因子の両方に関係するような観測変数は存在しない
- formativeな因子を構成する観測変数と,reflectiveな因子を構成する観測変数の間に共分散は全く無い
ということで,ここでは以下のシンプルなモデル( 図 7.30 )を考えてみましょう。
グラフィカルモデルにおいてformativeな構成概念は,一般的には六角形で示されているようです。 したがってこのモデルでは,gender,age,educationの3つの変数の(重み付け)合計点のような形で,demoという構成概念を形作っていると考えています。 これは,社会経済的地位(SCS)が複数の側面から評価されているのと構造的には同じことです36。
あとはこのモデルをlavaanの形式に落とし込んでいくだけです。 lavaanでformativeな測定を行う場合には,<~という記号を使用します。
あとは通常通りsem()関数を実行するだけです。 ただし,ここもいくつかの(lavaanパッケージ側の)制約があるため,引数に注意してください。
- (勾配の)計算を数値計算で行う必要があるため
optim.gradient = "numerical"を与える std.lv = TRUEに対応していないので,これは入れない(つまり必ず各構成概念の最初の項目の因子負荷・重みを1とした計算が行われる)- 標準化解を出したい場合は,
summary()関数で対応する
- 標準化解を出したい場合は,
lavaanでformativeな測定
lavaan 0.6-20 ended normally after 56 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 9
Used Total
Number of observations 2232 2432
Model Test User Model:
Test statistic 61.362
Degrees of freedom 6
P-value (Chi-square) 0.000
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_A =~
Q1_1 1.000 0.628 0.452
Q1_2 1.415 0.104 13.666 0.000 0.889 0.774
Q1_3 1.242 0.078 15.860 0.000 0.780 0.608
Composites:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
demo <~
gender 1.000 1.933 0.908
age 0.017 0.005 3.805 0.000 0.033 0.356
education 0.035 0.040 0.877 0.381 0.068 0.076
Regressions:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_A ~
demo 0.357 0.033 10.864 0.000 0.294 0.294
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
gender ~~
age 0.228 0.228 0.046
education 0.003 0.003 0.005
age ~~
education 2.954 2.954 0.249
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Q1_1 1.537 0.053 28.833 0.000 1.537 0.796
.Q1_2 0.530 0.056 9.436 0.000 0.530 0.402
.Q1_3 1.037 0.052 19.995 0.000 1.037 0.630
gender 0.220 0.220 1.000
age 113.790 113.790 1.000
education 1.236 1.236 1.000
.f_A 0.361 0.043 8.401 0.000 0.914 0.914
demo 0.268 1.000 1.000ということで得られた推定値(標準化解)を 図 7.31 に書き入れると,以下のようになります。
7.14 (おまけ)lavaanで探索的因子分析
2023年1月にリリースされたバージョン0.6-13以降では,lavaanパッケージで探索的因子分析が可能になっています。 ただの探索的因子分析ならpsych::fa()で十分なのですが,lavaanではSEMの枠組みと組み合わせることでEFAとCFAや回帰分析を組み合わせることができる点が,もしかしたら便利かもしれません。 こうしたモデルは特にExploratory SEM (ESEM: Asparouhov & Muthén, 2009)と呼ばれている比較的新しい手法です。 世間の注目を集めているかはわかりません。 ということでこのおまけセクションでは,lavaanで探索的因子分析およびESEMを行う方法を紹介していきます。
7.14.1 lavaanでEFAを試してみる
まずは普通に探索的因子分析を試してみます。 セクション 6.3 の10項目2因子モデル ( 図 6.6 ) を再現してみましょう。 lavaanでEFAを指定する方法は大きく分けると2種類です。
efa()関数
シンプルな方法は,efa()関数を利用するものです。
This is lavaan 0.6-20 -- running exploratory factor analysis
Estimator ML
Rotation method OBLIMIN OBLIQUE
Oblimin gamma 0
Rotation algorithm (rstarts) GPA (30)
Standardized metric TRUE
Row weights None
Number of observations 2432
Fit measures:
aic bic sabic chisq df pvalue cfi rmsea
nfactors = 2 78530.51 78698.61 78606.47 375.946 26 0 0.932 0.074
Eigenvalues correlation matrix:
ev1 ev2 ev3 ev4 ev5 ev6 ev7 ev8 ev9
3.078 1.834 0.896 0.823 0.722 0.684 0.530 0.523 0.469
ev10
0.440
Standardized loadings: (* = significant at 1% level)
f1 f2 unique.var communalities
Q1_1 0.408* * 0.846 0.154
Q1_2 0.661* 0.558 0.442
Q1_3 0.779* * 0.408 0.592
Q1_4 0.464* .* 0.723 0.277
Q1_5 0.624* 0.603 0.397
Q1_6 0.567* 0.690 0.310
Q1_7 0.623* 0.615 0.385
Q1_8 0.551* 0.689 0.311
Q1_9 0.691* 0.527 0.473
Q1_10 * 0.587* 0.634 0.366
f2 f1 total
Sum of sq (obliq) loadings 1.876 1.832 3.707
Proportion of total 0.506 0.494 1.000
Proportion var 0.188 0.183 0.371
Cumulative var 0.188 0.371 0.371
Factor correlations: (* = significant at 1% level)
f1 f2
f1 1.000
f2 0.317* 1.000 回転方法を指定する引数はrotationです。psych::fa()ではrotateだったのでご注意ください。 ということで,かなり簡単にlavaanの出力形式でEFAの結果を出すことができました。 lavaan::efa()の利点の一つは,自動的に因子負荷の検定を行ってくれるところです。 SEMの枠組みにしたがって,回転後の因子負荷が0であるという帰無仮説のもとで検定をしています。 デフォルトでは1%水準で有意のところに*がつくようになっていますが,これも引数で調整可能です。 ついでに因子負荷が小さいところも全て表示されるように書き換えてみましょう。
This is lavaan 0.6-20 -- running exploratory factor analysis
Estimator ML
Rotation method OBLIMIN OBLIQUE
Oblimin gamma 0
Rotation algorithm (rstarts) GPA (30)
Standardized metric TRUE
Row weights None
Number of observations 2432
Fit measures:
aic bic sabic chisq df pvalue cfi rmsea
nfactors = 2 78530.51 78698.61 78606.47 375.946 26 0 0.932 0.074
Eigenvalues correlation matrix:
ev1 ev2 ev3 ev4 ev5 ev6 ev7 ev8 ev9
3.078 1.834 0.896 0.823 0.722 0.684 0.530 0.523 0.469
ev10
0.440
Standardized loadings: (* = significant at 5% level)
f1 f2 unique.var communalities
Q1_1 0.408* -0.069* 0.846 0.154
Q1_2 0.661* 0.011 0.558 0.442
Q1_3 0.779* -0.032* 0.408 0.592
Q1_4 0.464* 0.142* 0.723 0.277
Q1_5 0.624* 0.019 0.603 0.397
Q1_6 -0.036 0.567* 0.690 0.310
Q1_7 -0.008 0.623* 0.615 0.385
Q1_8 0.022 0.551* 0.689 0.311
Q1_9 -0.012 0.691* 0.527 0.473
Q1_10 0.049* 0.587* 0.634 0.366
f2 f1 total
Sum of sq (obliq) loadings 1.876 1.832 3.707
Proportion of total 0.506 0.494 1.000
Proportion var 0.188 0.183 0.371
Cumulative var 0.188 0.371 0.371
Factor correlations: (* = significant at 5% level)
f1 f2
f1 1.000
f2 0.317* 1.000 ちなみにlavaanのデフォルトでは,最尤法によってパラメータの推定を行っています。 したがって,上記の結果はpsych::fa()でfm = "ml"を指定したときに同じになるはずです。
psych::fa()関数と比べる
分散説明率のところには細かい違いはあるのですが,因子負荷に関しては確かに同じ結果が得られました。
あえてlavaan::efa()関数を使う別の利点は,複数の因子数を一気に実行できることです。 引数nfactorsに整数のベクトルを与えてあげると,すべての因子数で実行した結果をまとめて一つのオブジェクトで返してくれます。
This is lavaan 0.6-20 -- running exploratory factor analysis
Estimator ML
Rotation method GEOMIN OBLIQUE
Geomin epsilon 0.001
Rotation algorithm (rstarts) GPA (30)
Standardized metric TRUE
Row weights None
Number of observations 2432
Overview models:
aic bic sabic chisq df pvalue cfi rmsea
nfactors = 1 80259.06 80374.99 80311.44 2122.495 35 0 0.595 0.157
nfactors = 2 78530.51 78698.61 78606.47 375.946 26 0 0.932 0.074
nfactors = 3 78387.85 78602.32 78484.76 217.286 18 0 0.961 0.067
Eigenvalues correlation matrix:
ev1 ev2 ev3 ev4 ev5 ev6 ev7 ev8 ev9
3.078 1.834 0.896 0.823 0.722 0.684 0.530 0.523 0.469
ev10
0.440
Number of factors: 1
Standardized loadings: (* = significant at 1% level)
f1 unique.var communalities
Q1_1 .* 0.934 0.066
Q1_2 0.502* 0.748 0.252
Q1_3 0.523* 0.727 0.273
Q1_4 0.487* 0.763 0.237
Q1_5 0.480* 0.769 0.231
Q1_6 0.439* 0.808 0.192
Q1_7 0.507* 0.742 0.258
Q1_8 0.480* 0.769 0.231
Q1_9 0.552* 0.696 0.304
Q1_10 0.531* 0.718 0.282
f1
Sum of squared loadings 2.327
Proportion of total 1.000
Proportion var 0.233
Cumulative var 0.233
Number of factors: 2
Standardized loadings: (* = significant at 1% level)
f1 f2 unique.var communalities
Q1_1 0.407* * 0.846 0.154
Q1_2 0.660* 0.558 0.442
Q1_3 0.778* 0.408 0.592
Q1_4 0.464* .* 0.723 0.277
Q1_5 0.623* 0.603 0.397
Q1_6 0.567* 0.690 0.310
Q1_7 0.622* 0.615 0.385
Q1_8 0.550* 0.689 0.311
Q1_9 0.690* 0.527 0.473
Q1_10 0.587* 0.634 0.366
f2 f1 total
Sum of sq (obliq) loadings 1.876 1.831 3.707
Proportion of total 0.506 0.494 1.000
Proportion var 0.188 0.183 0.371
Cumulative var 0.188 0.371 0.371
Factor correlations: (* = significant at 1% level)
f1 f2
f1 1.000
f2 0.309* 1.000
Number of factors: 3
Standardized loadings: (* = significant at 1% level)
f1 f2 f3 unique.var communalities
Q1_1 0.408* .* 0.798 0.202
Q1_2 0.671* * 0.555 0.445
Q1_3 0.796* 0.400 0.600
Q1_4 0.475* .* 0.725 0.275
Q1_5 0.636* 0.601 0.399
Q1_6 0.379* 0.448* 0.637 0.363
Q1_7 0.472* 0.492* 0.496 0.504
Q1_8 .* 0.472* 0.709 0.291
Q1_9 0.793* 0.386 0.614
Q1_10 0.600* 0.614 0.386
f1 f3 f2 total
Sum of sq (obliq) loadings 1.873 1.714 0.491 4.079
Proportion of total 0.459 0.420 0.120 1.000
Proportion var 0.187 0.171 0.049 0.408
Cumulative var 0.187 0.359 0.408 0.408
Factor correlations: (* = significant at 1% level)
f1 f2 f3
f1 1.000
f2 0.142 1.000
f3 0.325* 0.076 1.000 出力されるオブジェクトは,あくまでもlavaanの形式に沿っているため,例えばfitMeasures()関数を利用して(SEM的な)適合度指標を出して,因子数を決める参考にすることも可能だったりします。
nfct=1 nfct=2 nfct=3
npar 19.000 29.000 37.000
fmin 0.436 0.077 0.045
chisq 2122.495 375.946 217.286
df 35.000 26.000 18.000
pvalue 0.000 0.000 0.000
baseline.chisq 5201.585 5201.585 5201.585
baseline.df 45.000 45.000 45.000
baseline.pvalue 0.000 0.000 0.000
cfi 0.595 0.932 0.961
tli 0.480 0.883 0.903
nnfi 0.480 0.883 0.903
rfi 0.475 0.875 0.896
nfi 0.592 0.928 0.958
pnfi 0.460 0.536 0.383
ifi 0.596 0.932 0.962
rni 0.595 0.932 0.961
logl -40109.529 -39236.255 -39156.925
unrestricted.logl -39048.282 -39048.282 -39048.282
aic 80259.058 78530.510 78387.849
bic 80374.987 78698.607 78602.319
ntotal 2432.000 2432.000 2432.000
bic2 80311.443 78606.467 78484.761
rmsea 0.157 0.074 0.067
rmsea.ci.lower 0.151 0.068 0.060
rmsea.ci.upper 0.162 0.081 0.076
rmsea.ci.level 0.900 0.900 0.900
rmsea.pvalue 0.000 0.000 0.000
rmsea.close.h0 0.050 0.050 0.050
rmsea.notclose.pvalue 1.000 0.087 0.006
rmsea.notclose.h0 0.080 0.080 0.080
rmr 0.201 0.065 0.049
rmr_nomean 0.201 0.065 0.049
srmr 0.115 0.034 0.026
srmr_bentler 0.115 0.034 0.026
srmr_bentler_nomean 0.115 0.034 0.026
crmr 0.127 0.038 0.028
crmr_nomean 0.127 0.038 0.028
srmr_mplus 0.115 0.034 0.026
srmr_mplus_nomean 0.115 0.034 0.026
cn_05 58.064 252.548 324.123
cn_01 66.704 296.256 390.563
gfi 0.800 0.970 0.982
agfi 0.685 0.936 0.946
pgfi 0.509 0.458 0.322
mfi 0.651 0.931 0.960
ecvi 0.888 0.178 0.120今回の結果では,どうやら2因子モデルよりも3因子モデルのほうがモデル適合度は高いようです。 ただこのあたりは因子分析のときにお話したように,最終的には解釈可能性までを視野に入れて決めるようにしましょう。
モデル式で指定する
lavaanでEFAを実行するもう一つの方法は,「モデル式でEFAであることを指定する」というものです。 これまでにこのChapterでは,変数名の前に0*をつけることでその値を固定したり( セクション 7.7.1 ),名前をつけることで等値制約を置く方法( セクション 7.10 )を紹介しました。 これと同じ要領で,因子名の前に「この因子にどの項目がかかるかはEFA的に決めてください」ということを指定する記号を書き足すことができるのです。
EFA的に推定&回転をしてほしい因子名の前にefa()という記号をかけてあげます。 カッコの中は特に指定はありません(後で説明)。 とりあえずここではF1とF2の間のEFAであることがわかりやすいように"f12"としましたが,例えばefa("hoge")*f1 =~などとしても(f1とf2に同じ名前がついていれば)OKです。
lavaan 0.6-20 ended normally after 1 iteration
Estimator ML
Optimization method NLMINB
Number of model parameters 31
Row rank of the constraints matrix 2
Rotation method OBLIMIN OBLIQUE
Oblimin gamma 0
Rotation algorithm (rstarts) GPA (30)
Standardized metric TRUE
Row weights None
Number of observations 2432
Model Test User Model:
Test statistic 375.946
Degrees of freedom 26
P-value (Chi-square) 0.000
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f1 =~ f12
Q1_1 0.574 0.034 17.024 0.000 0.574 0.408
Q1_2 0.775 0.026 29.811 0.000 0.775 0.661
Q1_3 1.017 0.028 36.231 0.000 1.017 0.779
Q1_4 0.686 0.034 20.081 0.000 0.686 0.464
Q1_5 0.788 0.028 27.908 0.000 0.788 0.624
Q1_6 -0.044 0.024 -1.878 0.060 -0.044 -0.036
Q1_7 -0.011 0.023 -0.459 0.646 -0.011 -0.008
Q1_8 0.029 0.025 1.133 0.257 0.029 0.022
Q1_9 -0.016 0.020 -0.795 0.427 -0.016 -0.012
Q1_10 0.079 0.031 2.592 0.010 0.079 0.049
f2 =~ f12
Q1_1 -0.097 0.033 -2.981 0.003 -0.097 -0.069
Q1_2 0.013 0.020 0.682 0.495 0.013 0.011
Q1_3 -0.042 0.015 -2.731 0.006 -0.042 -0.032
Q1_4 0.210 0.033 6.430 0.000 0.210 0.142
Q1_5 0.024 0.023 1.056 0.291 0.024 0.019
Q1_6 0.699 0.028 24.527 0.000 0.699 0.567
Q1_7 0.820 0.030 27.497 0.000 0.820 0.623
Q1_8 0.709 0.030 23.759 0.000 0.709 0.551
Q1_9 0.951 0.031 31.181 0.000 0.951 0.691
Q1_10 0.958 0.037 25.724 0.000 0.958 0.587
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f1 ~~
f2 0.317 0.025 12.921 0.000 0.317 0.317
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Q1_1 1.672 0.051 32.747 0.000 1.672 0.846
.Q1_2 0.767 0.029 26.155 0.000 0.767 0.558
.Q1_3 0.695 0.037 18.788 0.000 0.695 0.408
.Q1_4 1.585 0.050 31.457 0.000 1.585 0.723
.Q1_5 0.962 0.035 27.799 0.000 0.962 0.603
.Q1_6 1.046 0.036 29.327 0.000 1.046 0.690
.Q1_7 1.064 0.039 27.338 0.000 1.064 0.615
.Q1_8 1.142 0.038 29.675 0.000 1.142 0.689
.Q1_9 0.998 0.041 24.060 0.000 0.998 0.527
.Q1_10 1.687 0.059 28.395 0.000 1.687 0.634
f1 1.000 1.000 1.000
f2 1.000 1.000 1.000だいぶlavaanの見慣れた形で出力されてくれました。 結果はもちろんlavaan::efa()のときと同じ値なので説明は省略します。
実際のところ,EFAをするだけであればefa()関数を使っておけば良いと思います37。 モデル式での指定方法は,このあとのESEMで必要になってくるのです…。
7.14.2 Exploratory SEM (ESEM)
ESEMは,SEMとEFAを組み合わせたようなものです。 この背景には,そもそもCFAを探索的に使っているケースが割と存在する,ということがあるようです (Browne, 2001)。 例えば セクション 7.7 で紹介したように,モデルの適合度を改善するためにある場所にパスを足したり引いたりすることは,まさにexploratoryといって良いでしょう。 また,自分で作成した尺度や,手元のデータで因子構造が再現できる怪しいデータを用いてSEMを実行する場合には,通常まずEFAで因子構造・因子得点を出した上で,これをSEMの中に投入することが多くあります。 ならばもういっそ全部ひっくるめて一気にやってしまおう,というモチベーションもあるのかもしれません。
ということでESEMを試してみましょう。ここでは 図 7.32 のようなモデルを考えてみます。 左側の6項目と右側の6項目は,それぞれ異なる尺度を表しています(以後,左側を尺度A,右側を尺度Bと呼びます)。 想定する因子数だけは決まっていて,それぞれが2因子を測定する尺度です。 さらに,尺度Aの一方の因子が尺度Bの一方の因子に影響を与える,という因子間の関係性(回帰)も仮説として検証したいとします。
このモデルをSEMで実行する場合には,尺度A・Bの中の各項目がそれぞれどちらの因子に所属するかを明確に決める必要がありました。 図 7.32 で言えば,青い点線のところにパスを許容しない(=因子負荷は厳密にゼロとする)のがSEMでした。 一方ESEMでは,この青い点線のパス (cross-loadings) を許容します38。 つまり,尺度Aに含まれる2因子(\(f_1, f_2\))は6項目からEFAによって推定し,尺度Bの6項目からも同様に2因子(\(f_3, f_4\))を推定する,ということです。 そして,小さい因子負荷もそのまま残してSEMの適合度指標の計算などを行います。 言い換えると,ESEMはSEMの制約を緩めたモデルあるいはEFAに部分的な制約を加えたモデルという位置づけになっているわけです。
では実際に 図 7.32 のESEMモデルを書き下してみましょう。 先程出てきたefa("")*の記法を使って書いていきます。
model_esem <- '
# 尺度AのEFA
efa("f12")*f1 =~ Q1_1 + Q1_2 + Q1_3 + Q1_6 + Q1_7 + Q1_8
efa("f12")*f2 =~ Q1_1 + Q1_2 + Q1_3 + Q1_6 + Q1_7 + Q1_8
# 尺度BのEFA
efa("f34")*f3 =~ Q1_11 + Q1_12 + Q1_13 + Q1_16 + Q1_17 + Q1_18
efa("f34")*f4 =~ Q1_11 + Q1_12 + Q1_13 + Q1_16 + Q1_17 + Q1_18
# 因子間の回帰
f3 ~ f1
f4 ~ f2
'尺度Aと尺度Bはそれぞれ異なる因子を測定しているため,例えばQ1_1がf3やf4にかかることはありません(因子負荷は0)。 そして因子の回転は,「f1とf2が単純構造に近づくように」「f3とf4が単純構造に近づくように」を独立に実行していきます。 このことを表すために,f1とf2の前にはefa("f12")*,f3とf4の前にはefa("f34")*というように,異なる名前のefaをかけているのです。
あとは推定するだけです。
lavaan 0.6-20 ended normally after 29 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 40
Row rank of the constraints matrix 4
Rotation method OBLIMIN OBLIQUE
Oblimin gamma 0
Rotation algorithm (rstarts) GPA (30)
Standardized metric TRUE
Row weights None
Number of observations 2432
Model Test User Model:
Test statistic 422.462
Degrees of freedom 42
P-value (Chi-square) 0.000
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f1 =~ f12
Q1_1 0.607 0.034 17.755 0.000 0.607 0.432
Q1_2 0.856 0.029 29.726 0.000 0.856 0.730
Q1_3 0.909 0.032 28.397 0.000 0.909 0.696
Q1_6 -0.021 0.021 -0.996 0.319 -0.021 -0.017
Q1_7 -0.017 0.016 -1.039 0.299 -0.017 -0.013
Q1_8 0.099 0.028 3.559 0.000 0.099 0.077
f2 =~ f12
Q1_1 -0.067 0.033 -2.028 0.043 -0.067 -0.048
Q1_2 0.003 0.015 0.179 0.858 0.003 0.002
Q1_3 0.013 0.019 0.660 0.509 0.013 0.010
Q1_6 0.763 0.034 22.180 0.000 0.763 0.620
Q1_7 0.930 0.038 24.354 0.000 0.930 0.707
Q1_8 0.634 0.033 19.016 0.000 0.634 0.493
f3 =~ f34
Q1_11 0.880 0.034 25.566 0.000 1.037 0.636
Q1_12 0.979 0.037 26.402 0.000 1.153 0.716
Q1_13 0.649 0.028 23.054 0.000 0.765 0.568
Q1_16 0.024 0.013 1.822 0.068 0.028 0.018
Q1_17 -0.011 0.014 -0.788 0.431 -0.013 -0.008
Q1_18 -0.039 0.023 -1.695 0.090 -0.046 -0.029
f4 =~ f34
Q1_11 0.111 0.024 4.606 0.000 0.111 0.068
Q1_12 -0.120 0.021 -5.669 0.000 -0.121 -0.075
Q1_13 0.082 0.023 3.491 0.000 0.082 0.061
Q1_16 1.351 0.030 45.238 0.000 1.355 0.861
Q1_17 1.272 0.029 43.650 0.000 1.277 0.834
Q1_18 1.036 0.031 32.966 0.000 1.040 0.653
Regressions:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f3 ~
f1 0.637 0.039 16.261 0.000 0.541 0.541
f4 ~
f2 -0.053 0.027 -1.971 0.049 -0.052 -0.052
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f1 ~~
f2 0.264 0.028 9.314 0.000 0.264 0.264
.f3 ~~
.f4 -0.220 0.028 -7.764 0.000 -0.220 -0.220
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Q1_1 1.623 0.051 31.654 0.000 1.623 0.822
.Q1_2 0.641 0.037 17.164 0.000 0.641 0.466
.Q1_3 0.872 0.045 19.547 0.000 0.872 0.512
.Q1_6 0.942 0.045 20.888 0.000 0.942 0.621
.Q1_7 0.874 0.059 14.784 0.000 0.874 0.505
.Q1_8 1.212 0.043 28.146 0.000 1.212 0.731
.Q1_11 1.619 0.066 24.478 0.000 1.619 0.610
.Q1_12 1.190 0.066 18.083 0.000 1.190 0.459
.Q1_13 1.252 0.045 27.828 0.000 1.252 0.689
.Q1_16 0.657 0.044 14.817 0.000 0.657 0.265
.Q1_17 0.705 0.041 17.221 0.000 0.705 0.301
.Q1_18 1.431 0.048 30.098 0.000 1.431 0.564
f1 1.000 1.000 1.000
f2 1.000 1.000 1.000
.f3 1.000 0.720 0.720
.f4 1.000 0.993 0.993無事,小さい因子負荷を残して推定が完了しました。 ESEMの利点は,このように小さい因子負荷を許容することでモデル適合度がSEMよりも良くなる可能性がある,という点にあります。 試しに 図 7.32 から青い点線を取り除いたSEMモデルと適合度を比べてみましょう。
model_sem <- "
# 尺度A
f1 =~ Q1_1 + Q1_2 + Q1_3
f2 =~ Q1_6 + Q1_7 + Q1_8
# 尺度B
f3 =~ Q1_11 + Q1_12 + Q1_13
f4 =~ Q1_16 + Q1_17 + Q1_18
# 因子間の回帰
f3 ~ f1
f4 ~ f2
"
# 推定
result_sem <- sem(model_sem, data = dat, std.lv = TRUE)
# 適合度の比較
# SEMはESEMの特殊なケース(一部の因子負荷を0に固定)なのでnested
summary(compareFit(result_esem, result_sem))################### Nested Model Comparison #########################
Chi-Squared Difference Test
Df AIC BIC Chisq Chisq diff RMSEA Df diff Pr(>Chisq)
result_esem 42 96399 96607 422.46
result_sem 50 96485 96647 524.93 102.47 0.069681 8 < 2.2e-16
result_esem
result_sem ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
####################### Model Fit Indices ###########################
chisq df pvalue rmsea cfi tli srmr aic
result_esem 422.462† 42 .000 .061† .944† .913† .046† 96398.512†
result_sem 524.928 50 .000 .062 .931 .908 .054 96484.978
bic
result_esem 96607.185†
result_sem 96647.279
################## Differences in Fit Indices #######################
df rmsea cfi tli srmr aic bic
result_sem - result_esem 8 0.001 -0.014 -0.004 0.007 86.466 40.094今回の比較では,ESEMの結果の方が適合度が良いことがわかります。 特に青い点線にあたるところに0ではない因子負荷があるような場合には,SEMで無理に0に制約をかけてしまうと適合度が悪化してしまう可能性がある,ということですね。
実際には
cov()関数で得られるのは不偏共分散行列です。\(\symbf{S}\)は標本共分散行列なので,\(P/P-1\)倍する必要があったりするのですが,今回は2000人以上いるので気にしないことにします。↩︎もちろんこれも厳密にはポリコリック相関のほうが良い可能性が高いですが,ここでは深く考えずにとりあえずピアソンの積率相関係数で話を進めます。↩︎
理論的には\(T\)因子構造の場合,因子負荷行列のうち最低でも\(T(T-1)\)個の値を固定したら推定は可能です。↩︎
残念ながら固有値分解によって因子負荷行列を求めることはできなくなりますが,コンピュータによる反復計算ならば力技で近い値を求めることができるでしょう。↩︎
本当は
lavaanパッケージの基本関数は同名のlavaan()というものです。 この関数ではモデルの推定のための設定をいろいろと細かく変更できるのですが,その設定が割と細い上にデフォルトでは思っていたような設定になかなかたどり着けません。いわば上級者向けの関数です。↩︎平均構造も統一的な枠組みで扱うために,近年では「共分散構造分析」ではなく「構造方程式モデリング」という呼び方が一般的なのだと思ってます。↩︎
パス解析での誤差項は潜在変数としても扱われないため,楕円で囲わないのが一般的です。↩︎
「途中で
Q1_Aを通っているじゃないか」という点は大目に見てください。SEMでは全ての内生変数の分散・共分散を外生変数の分散の関数で表す必要があるため,パスの経路で考える場合には必ず外生変数を通過する必要があるのです。↩︎共通因子と独自因子の間は無相関であり,またモデル上独自因子間も無相関と仮定しているため,これらの項が全て消えています。↩︎
ちなみにこれで表示される画面は,https://lavaangui.org/からもアクセス可能です。↩︎
独立モデルとは反対に,全ての観測変数間に両方向の矢印を引いたモデル(共分散を独立に推定するモデル)のことを飽和モデル(フルモデル)と呼びます。わざわざ飽和モデルをSEMで実行する必要はまったくないのですが「全てのモデルは独立モデルと飽和モデルの間に位置している」という感覚は持っておくと良いかもしれません。↩︎
もう少し詳しく説明すると,\(L_h\)は「対立仮説を飽和モデルとしたときの\(\symbf{\Sigma}\)の尤度比検定統計量」になっています。尤度比検定では,\(L_h\)つまり乖離度が大きい場合には対立仮説が採択されるため,「いま考えているモデル\(\symbf{\Sigma}\)よりは飽和モデルが真のモデル構造と考えられる」となります。↩︎
ちなみに\(L_{h}\)や\(L_{0}\)を\(P-1\)で割ったものの期待値は,対応する自由度に一致することが知られています。つまり,自由度が小さいほど=パラメータ数が多いほどズレの期待値は当然のように小さくなるわけです。↩︎
summary()に引数fit = TRUEを与えても良いのですが,この方法だと一部の適合度指標しか出してくれません。↩︎同じように,
1*としたら1に固定したりもできます。0以外はあまり使い道ないかもしれませんが…↩︎「自由推定になっていない」ということは,例えば
1*によって係数を0以外の定数に固定している場所も検討対象にしてくれる,ということです。↩︎外生変数の
genderも二値のカテゴリカル変数じゃないか,と思われるかもしれませんがそこは一旦おいといてください。↩︎以前のバージョンでは,
Intercepts:にも自動的に.educationの値が表示されていたような気がするのですが,いつの間にか無くなっていました。ただ,モデル式にeducation ~ 0を追加(切片を0に固定)しても結果は全く変わらないことから,平均値は0に固定されていることが分かります。↩︎ダミー変数を作るためのパッケージとして
makedummiesというものもあります。こちらはデータフレーム内のfactor型変数を一気に全部ダミー変数に変えてくれるものです。用途に応じて使い分けると良いでしょう(ただ2019年が最終更新なので急に使えなくなるかも)。↩︎因子得点から観測変数への回帰を含むモデルにおいて
ordered = TRUEにすると,内生変数となった観測変数も自動的にカテゴリ変数として扱われます。このように観測変数の回帰と因子分析を組み合わせた場合には意図せぬカテゴリ化を行ってしまう可能性があるので気をつけましょう。↩︎多母集団同時分析以外でも切片を考えても良いのですが,グループ間での比較をしない限りはさほど重要ではないのでこれまで無視してきました。↩︎
下2つのモデルには決まった名称が無いため,カッコをつけています。↩︎
ここまでのプロセスの大半を一度にやってくれる関数として,
semTools::measurementInvariance()という関数があります。一応今のところは使えるのですが,やがて消えることが公式にアナウンスされています。「代わりにmeasEq.syntax()を使え」とアナウンスされているのですが,これは「指定した等値制約を置いたモデル式を作ってくれる関数」のようです。つまり,機械的にとりあえずいろいろな不変モデルを試すのではなく,一つ一つの結果を見て能動的に判断していけよということなのかもしれません。↩︎パラメータを自由推定にした際の適合度の改善を見るわけなので
modificationindices()も使えそうなのですが,こいつは「等値制約を外したとき」を評価してはくれないのでここでは使えません。↩︎一応他の因子との因子間相関(両方向の矢印)があれば,2項目でも問題なく推定できるようになりますが,安定しないことも多々あります…↩︎
Rに慣れた方は,試しに「変数間の相関関係を完全に無視してデータのサイズだけ合わせたデータ」を乱数生成して試してみてください。ほぼ確実に推定失敗すると思います。↩︎
独自因子の分散の真値がほぼゼロの場合,標本誤差の影響などで0を下回ってしまうことが実際にあるのです。そうだと言い切れるなら仕方ないのです。↩︎
もしこれに加えて\(H_5:c = 0\)が示せれば,完全な媒介効果だといえます。因果関係における中継点を見つけた,という意味で因果関係のメカニズム解明にかなり役立つ情報になりえます。↩︎
当然ですが,
totalの値はlm(education ~ gender,data=dat)の結果と一致します。↩︎AICやBICがぜんぜん違う値になっているのですが,この理由は分かりません…何か計算方法のせいだとは思うのですが,とりあえず今回のケースではAICやBICはあてにならないと思ってください。↩︎
少し前までは
semTools:reliability()という関数もあったのですが,すでにdeprecatedになっているのでsemTools::compRelSEM()を使います。↩︎このモデルはあくまでも仮想です。一応元ネタは Albers (2010) ですが,皆さんの知見に照らし合わせたときに「そんな因果関係なわけないだろ!」といった批判は甘んじて受け入れます。↩︎
その点で,PLS-SEMはcomposite-based SEMと呼ばれることもあるようです (Hwang et al., 2020)。略すとCB-SEMになってしまいますね…↩︎
その点で,PLS-SEMはvariance-based SEMと呼ばれることもあるようです。別名が多いですね。↩︎
もちろん,SCSとは全く無関係なので,このあとに示す結果は「どちらの性別のほうが優れている」「若いほうがナントカ」といったことを含意するものではありません。↩︎
もっと言えばここまでの話は
psych::fa()でも何一つ問題はないんですけどね。↩︎もちろん,そもそもどこのパスが黒か青かわからない(完全に探索的な)状態でもESEMは実行可能です。というかESEMの推定ではパスの色は区別していない,はず。↩︎