本章の構成
このChapterでは,データに階層性がある場合の分析方法を紹介していきます。 マルチレベルな分析の中でも最も基本的な階層線形モデルをRで実行する場合には,lme4というパッケージがデファクトスタンダードになっていると思うのですが,この資料では,同等の機能を持ちながらより多くの状況(e.g., 過分散,ゼロ過剰,不均一分散)に対応可能なglmmTMBパッケージを使用します1 2。
9.1 マルチレベルデータとは?
マルチレベルデータ(階層データ)とは,異なる階層レベルを含む構造を持ったデータのことを指します。 社会科学の多くの研究分野では,個人が何らかの集団に所属しているという自然な階層構造が存在します。 教育研究では生徒が学校に,医療研究では患者が病院に,経済研究では従業員が企業に所属するといった具合です。
まずは,「データに階層性がある」ということの具体的な意味を詳細に説明した上で,なぜそのようなデータに対しては特別な分析法が必要なのかを直感的および数理的に示していきます。
9.1.1 マルチレベルデータの例(使用するデータ)
本Chapterでは,これまでとは異なるデータを使用します(さすがにこれまで使ってきたものでは無理でした……)。
↓本Chapterで使用するファイルのダウンロードはこちらから
school_id student_id read_score wants_univ belong1 belong2 belong3
1 001 0462 704.541 1 3 2 3
2 001 0850 569.687 1 4 3 4
3 001 0893 647.678 1 4 3 4
4 001 1063 672.170 1 4 4 4
5 001 1234 671.836 1 3 2 3
belong4 belong5 belong6 teach1 teach2 teach3 teach4 escs
1 3 3 3 4 2 2 4 1.2045
2 4 4 4 4 4 3 4 -0.0486
3 4 3 4 4 4 4 4 -0.2250
4 3 3 1 4 4 2 3 0.4586
5 4 2 3 2 2 2 2 -0.3454
sch_escs_mean s_t_ratio
1 0.4668657 15.5
2 0.4668657 15.5
3 0.4668657 15.5
4 0.4668657 15.5
5 0.4668657 15.5
[ reached 'max' / getOption("max.print") -- omitted 1 rows ]このデータは,経済協力開発機構(OECD)がおよそ3年に1度実施している生徒の学習到達度調査(PISA)の2018年実施分の日本のデータを加工したものです。 表 9.1 に,各変数の意味をまとめました。
chapter09.rdsの変数
| 変数名 | 説明 |
|---|---|
student_id |
回答者(生徒)のID |
school_id |
回答者(生徒)が所属する学校のID |
read_score |
PISA読解力の得点 |
wants_univ |
予想する最終学歴(進学希望の代理指標として)「あなたは,自分がどの教育段階まで終えると思いますか。:短期大学・高等専門学校あるいは大学・大学院」 |
belong1 |
所属感「学校ではよそ者だ(またはのけ者にされている)と感じる」 |
belong2 |
所属感「学校ではすぐに友達ができる」 |
belong3 |
所属感「学校の一員だと感じている」 |
belong4 |
所属感「学校は気後れがして居心地が悪い」 |
belong5 |
所属感「他の生徒たちは私をよく思ってくれている」 |
belong6 |
所属感「学校にいると,さみしい」 |
teach1 |
授業方法「先生は,私たちの学習の目標をはっきりと示す」 |
teach2 |
授業方法「先生は,私たちが学んだことを理解しているかどうか、確認するための質問を出す」 |
teach3 |
授業方法「先生は,授業の始めに、前回の授業のまとめをする」 |
teach4 |
授業方法「先生は,学習する内容を私たちに話す」 |
escs |
回答者(生徒)の社会経済的地位 |
sch_escs_mean |
学校ごとのescsの平均値 |
s_t_ratio |
ST比(教員1人あたりの生徒の数) |
なお,本Chapterでは基本的に,「読解力に影響を与える要因」の検討を目的とします。 したがって,被説明変数は一貫してread_scoreです。
PISAでは,(層化)二段階抽出によってサンプリングを行っています。 これは,全国の高校生から,
- (学校区分ごとに)対象となる高校を無作為に選ぶ
- 選ばれた高校の中から,受検する学生をランダムに(クラス単位で)選ぶ
という手順で抽出する方法です。 したがって,このデータの分析単位(各行の単位)は生徒一人ひとりですが,同時に各生徒は特定の学校に所属しており,複数の生徒が同じ学校に所属しているという構造のデータになっています3。
興味がある人もいるかも知れないので,本Chapterで使用するデータセットの作成に使用したRコードを掲載しておきます。 あくまでも補足なので,本編では封印していたdplyrの記法を使いますがご了承ください。
まずは,PISAデータをダウンロードします。 RにはEdSurveyというパッケージがあり,これを使うとPISAをはじめとした大規模調査データを簡単に取得できます。
# install.packages("EdSurvey")
library(EdSurvey) # PISAをはじめとした大規模調査データの取得用
library(dplyr) # データフレームの操作用
library(stringr) # 文字列の操作用
# PISA2018のデータのダウンロード
# かなり大きい&時間がかかるので要注意!
downloadPISA(years = 2018, root = "./")
# 日本のデータだけ使うので準備
pisa_jpn_edsurvey <- readPISA(path = "./PISA/2018", countries = "JPN")
# 使用する変数の選択
selected_vars <- c(
"cntstuid", "cntschid", "pv1read", "escs",
"st225q05ha", "st225q06ha", # 進学希望
paste0("st034q", sprintf("%02i", 1:6), "ta"), # 所属感の項目
paste0("st102q", sprintf("%02i", 1:4), "ta"), # 授業方法の項目
"stratio"
)
# データの抽出
pisa_df_raw <- getData(
data = pisa_jpn_edsurvey,
varnames = selected_vars,
addAttributes = FALSE
)ここまででデータの準備ができたので,あとは分析しやすいように色々と整形していきます。
pisa_final <- pisa_df_raw |>
rename( # 分かりやすい変数名に変更
school_id = cntschid, student_id = cntstuid,
read_score = pv1read, wants_univ1 = st225q05ha, wants_univ2 = st225q06ha,
belong1 = st034q01ta, belong2 = st034q02ta, belong3 = st034q03ta,
belong4 = st034q04ta, belong5 = st034q05ta, belong6 = st034q06ta,
teach1 = st102q01ta, teach2 = st102q02ta, teach3 = st102q03ta, teach4 = st102q04ta,
s_t_ratio = stratio
) |>
# 進学希望有無を二値変数に変換
mutate(wants_univ = as.numeric(wants_univ1 == "CHECKED" | wants_univ2 == "CHECKED")) |>
# 欠損値を持つ行を削除 (簡単化のため)
na.omit() |>
# 所属感の項目を数値に変換し,逆転項目の向きを反転
mutate(across(starts_with("belong"), as.numeric)) |>
mutate(across(c(belong2, belong3, belong5), function(x) 5 - x)) |>
# 先生の指導に関する項目を数値に変換し,すべて逆転
mutate(across(starts_with("teach"), as.numeric)) |>
mutate(across(starts_with("teach"), function(x) 5 - x)) |>
# レベル2の変数(学校平均ESCS)を作成
group_by(school_id) |>
mutate(sch_escs_mean = mean(escs, na.rm = TRUE)) |>
ungroup() |>
# IDの桁数を削る(必須ではない)
mutate(
school_id = sprintf("%03s", str_sub(school_id, -3, -1)),
student_id = sprintf("%04s", str_sub(student_id, -4, -1))
) |>
select( # 不要な変数を削除し,列の順番を整理
school_id, student_id, read_score, wants_univ,
belong1:belong6, teach1:teach4, escs, sch_escs_mean, s_t_ratio
) |>
# 並び替え
arrange(school_id, student_id) |>
# data.frameとして保存(tibbleでも良いが,資料中の一貫性から)
as.data.frame()
saveRDS(pisa_final, "chapter09.rds")9.1.2 階層性が生じるメカニズム
階層性が生じる理由は大きく分けて以下の3つです。
- 選択効果(Selection Effect)
- 似たような特徴を持つ個人が同じ集団に集まる傾向です。 例えば,公立の学校では,家庭の社会経済的地位が似た生徒は同じ地域(学区)に住むことが多いため,同じ学校に通う傾向が見られるでしょう。
- 処遇効果(Treatment Effect)
- 同じ集団に属する個人は,共通の処遇や環境を経験することで結果的に似たような特徴を持つようになることがあります。 同じ学校の生徒は,共通の教員,カリキュラム,設備の影響を受けるために,学力や進路希望なども(学校ごとに)似たものになるでしょう。 あるいは,同じ会社に勤務している人は,仕事に対する考え方などが似てくるかもしれません。
- 相互作用効果(Interaction Effect:ピア効果とも)
- 同じ集団に属する個人同士は,行動などを共にする機会が多いことで相互に影響し合うことがあります。 その結果として,集団内で特徴が似てくることもあるでしょう。 例えば学校では,同級生同士の学習態度や動機が相互に影響し合うはずです。
このように,データの階層性(集団内で似ている傾向)は,事前的にも事後的にも発生しうるものです。 どのように発生したものにせよ,階層性がある場合にはこれを考慮して分析する必要があります。
その中でも,特に階層性の因果関係をはっきりさせたい場合には,階層性のメカニズム(どの時点で発生したものであるか)の区別が非常に重要です。 例えば,学校において「相互作用効果によって学習意欲が向上するか」を検証することはかなり難しいとされています。 これは,階層データでは本質的に「クラスメイトが頑張っているから自分も頑張ろう,となる(ピア効果)」のか「もともと同程度に頑張る=同程度の学力の人たちが同じ学校に所属しやすい(選択効果)」のかが区別できないためです。 つまり,「類は友を呼ぶ」のか「友が類になる」のかが区別できないと,因果関係の方向性を特定することができないのです。
9.1.3 階層性を考慮する必要性
階層データの根本的な特徴は,観測単位間の依存性にあります。 分析の対象となる変数について,観測単位に依存性がある場合,普通の回帰分析や分散分析で分析すると,いくつかの問題が生じます。 まずはその問題を直感的に理解するため,簡単な「母平均の推定」を例に考えてみましょう。
シンプルな例
PISAの目的の中には,「世界各国の高校1年生の学習到達度」の評価があります。 日本の高校1年生の読解力の平均値(母平均)を知るために最も適切な方法がランダムサンプリングであることは明らかです。 しかし,高校生一人ひとりに個別にお願いをするのはかなり大変なので,PISAでは先に説明した二段階抽出を行っています。 では,「ある学校のある1つのクラス(40人)をランダムに選ぶ」場合,「完全ランダムに40人をサンプリングする」理想的な状況と比べて,母平均の推定はどうなるでしょうか。
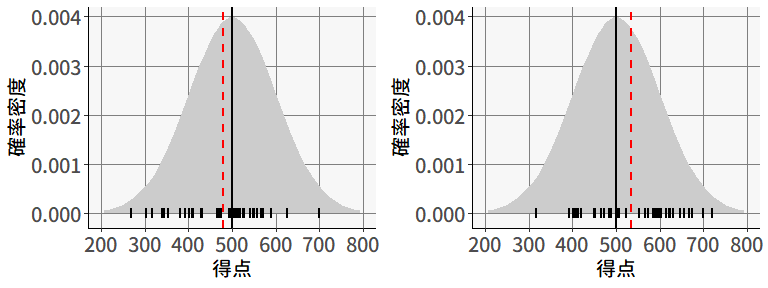
PISAの得点は,平均500,標準偏差100になるように調整された値なので,まずは理想的なランダムサンプリングを想定して,試しに正規分布\(N(500, 100^2)\)から40個の乱数を2回ほどサンプリングしてみましょう。 すると, 図 9.2 のような結果が得られました。
各図には,正規分布\(N(500, 100^2)\)の確率密度関数と,下のほうに実際にサンプリングされた40個の値が描かれています。 また,黒い直線は\(x=500\)を,赤い点線は標本平均を表しています。 このように,毎回のサンプリングは異なっていても,結果として得られる標本平均は,サンプルサイズに応じて母平均の周辺に集まる,という性質がありました(大数の法則)。
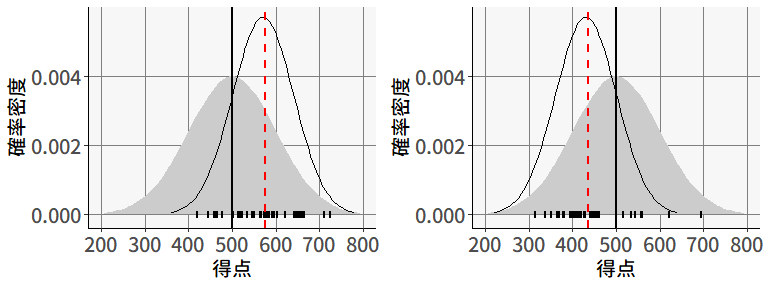
続いては,「ある学校のある1つのクラス(40人)をランダムに選ぶ」場合を考えてみます。 この場合,たまたま優秀な学校が選ばれる可能性もあれば,そうでもない学校が選ばれる可能性もあります。 図 9.3 の左は,たまたま優秀な学校が選ばれた場合を,右は優秀ではない学校が選ばれた場合を表しています。
この場合,あるクラスが抽出されると,そのクラスの中での学力レベルは全体の\(N(500, 100^2)\)よりも凝集していると考えられるため,その確率分布を線で表しています4。 その結果,図 9.2 と比べると,どのクラスが選ばれるかによって,標本平均は大きく変動することがわかります。
図 9.2 と 図 9.3 の対比は,データに階層性がある場合,理想的な状況と比べてサンプリングの効率が低下することを意味しています。 ここで,標本平均の標本分布は,サンプルサイズを用いて,正規分布\(N\left(\mu, \frac{\sigma^2}{n}\right)\)と表せることを思い出してください。 この式に基づくと,\(n=40\)の場合( 図 9.2 )の標本平均の標本分布は,\(N\left(500, \frac{100^2}{40}\right)\approx N(500, 15.81^2)\)となります。 そして,二段階抽出の場合( 図 9.3 )には,どうやら標本平均の標本分布の分散は,これよりも大きくなりそうなので,\(N\left(\mu, \frac{\sigma^2}{n}\right)\)に基づいて標本分布を構成してしまうと,色々と問題がありそうだと分かるのです5。
以上は,母平均の推定においてデータの階層性に注意して分析を行うべきであることの簡単な説明でした。 ほかの分析手法においても同様に,完全なランダムサンプリングを前提に構築された手法を,階層性のあるデータに適用すべきではないことが多々あるわけです。
生態学的誤謬
ここでもう一つ,データの階層性を無視することが明確に誤った結論を導く有名な例を紹介しておきます。
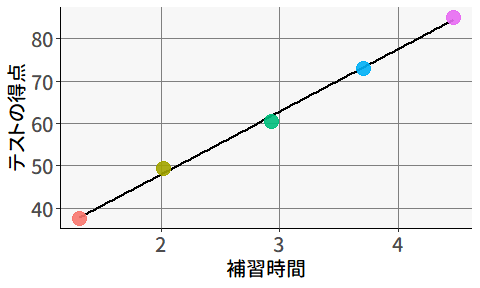
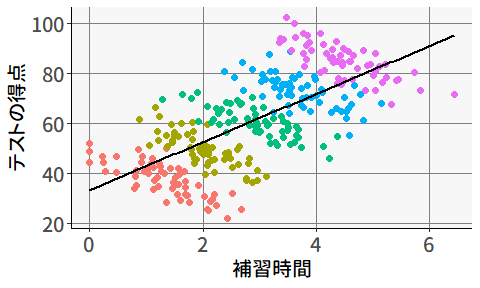
ある研究者が,「教育熱心な地域ほど学力が高い」という仮説を立てました。 これを検証するため,(「教育熱心度」の代理指標として)学校の授業以外の学習時間(塾・補習など)が長いほど学力が高いかを調べるために,5つの地域からそれぞれ60人ずつのデータを収集しました。 図 9.4 は,地域ごとに計算した平均値に基づいて回帰分析を行った結果です。
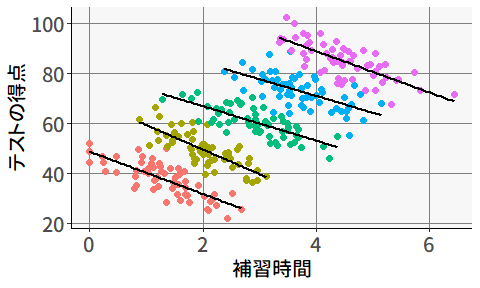
この結果を見ると,補習時間と学力の間にはかなり強い正の相関がありそうです。 ただし,この結果は「補習時間が長い個人ほど学力が高い」ということは意味しません。 実際に,個人レベルで見ても2つの変数に正の相関があるかは場合によります。 実際に,地域(散布図の点の色)ごとにそれぞれ回帰分析を行ってみると,個人レベルでは,補習時間が長いほどむしろテストの得点が低いことがわかります( 図 9.6 )。
このように,集団レベルで見られた関係性が,個人レベルにも自動的に当てはまる,ということは決してありません。 にも関わらず,個人と集団をごっちゃに考えてしまい誤った推論を行ってしまうことを,生態学的誤謬 (ecological fallacy: Robinson, 1950) と呼びます。 データの階層性を無視して分析を行うことは,生態学的誤謬の餌食になってしまう可能性があるわけです。
ちなみにこのデータに関しては,集団平均を使わずに個人レベルのデータでそのまま回帰分析を行った場合も,正の傾きが見られます( 図 9.6 )。
このように,データ全体を個人レベルで分析した場合と,集団ごとに分析した場合に全く異なる結論が導き出されることは,生態学的誤謬の中でもシンプソンのパラドックス (Simpson, 1951) などと呼ばれています。
生態学的誤謬およびシンプソンのパラドックスに関して厄介なのは,この場合どちらのメカニズムもある程度妥当な解釈が可能である,という点です。 図 9.5 に示されているように,補習時間が長いほどテストの得点が高くなる,というのは直感的に有り得そうですし, 図 9.5 のように集団内では負の関係が見られる,というのも,「もともとの学力が低い生徒ほど補習させられている」と考えると納得が行きます。
このため,階層データに対しては,データの階層性を正しく理解して適切な分析手法を適用するだけでなく,集団レベル・個人レベルの変数がどのように影響するかを考えることが重要となります。
9.1.4 階層構造の表現
ここで,これ以降の説明のために,階層構造の基本的な表記を説明しておきます。 必然的に添え字が複数になるので,混乱しないように気をつけてください。 本資料では,階層データのレベルに合わせて添字を以下のように表します6。
- レベル1(個人[\(p\)erson]レベル): \(p = 1, 2, \ldots, n_g\)(第\(g\)集団内の個人)
- レベル2(集団[\(g\)roup]レベル): \(g = 1, 2, \ldots, G\)(集団)
例えば\(x_{pg}\)は,「第\(g\)集団の中の\(p\)番目の人の\(x\)の値」を表しているわけです。
なお,レベル1が「個人」,レベル2が「集団」を表す,というのは,あくまでも本Chapterで使用するPISAのデータに関する話です。 これ以外にも,例えば同じ人から定期的に何度も測定を行うことで変化を観察する(縦断的な)測定の場合には,レベル1が「時点」,レベル2が「個人」となります。
また,理論的には階層はいくつでも考えることができます。 例えばPISAデータの場合には,国\(\rightarrow\)学校\(\rightarrow\)個人という3つの階層を考えることもできますし,アメリカであれば州ごとにも教育政策が異なるため,国\(\rightarrow\)州\(\rightarrow\)学校\(\rightarrow\)個人という4つの階層を考えることもできるでしょう。
もちろん階層を増やすほど,分析のモデルは複雑になり,必要なサンプルサイズも増加します。 ただ,理論的には考えることはできるので,本当に必要な時が来たら考えてみてください。
9.1.5 変動の分解
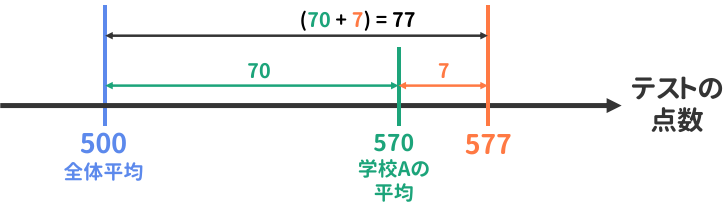
データの階層性を考慮するためには,まずある変数の値のばらつきが複数の要素に分解されるという考え方を理解する必要があります。 例えば,PISAの平均点が570点のとあるクラスの生徒が577点を獲得した場合,これは \[ x_{pg} = 500 + \overbrace{70}^{全体平均とクラス平均の差} + \overbrace{7}^{クラス平均との差} = 577 \tag{9.1}\] と表すことができます( 図 9.7 )。 このとき,「全体平均とクラス平均の差」は,言わば集団レベルの変動を意味しています。 一方「クラス平均との差」は,集団内での個人レベルの変動を意味します。
分解に基づく回帰分析の表現
このように変数を「全体平均と集団の平均の差」と「集団の平均と個人の値の差」に分解すると,単回帰分析は \[ \begin{alignedat}{3} y_{pg} &= \beta_0 + & &\beta_1x_{pg} & &+ u_{pg} \\ &= \beta_0 + & &\beta_1[(x_{pg}-\bar{x}_{\cdot g})+\bar{x}_{\cdot g}] & &+ u_{pg} \end{alignedat} \tag{9.2}\] と表すことができます。 ここで,\(\bar{x}_{\cdot g}\)は集団\(g\)の平均値 \[ \bar{x}_{\cdot g} = \frac{1}{n_g} \sum_{p=1}^{n_g}x_{pg} \tag{9.3}\] を表しています。 (9.2)式からは,回帰分析における傾き\(\beta_1\)が集団レベルと個人レベルの両方の変動に対して影響する係数であることが分かります。 これは,例えば\(\beta_1>0\)であった場合に,
- \((x_{pg}-\bar{x}_{\cdot g})\)の値が大きい,すなわち集団内で相対的に値が大きい個人ほど\(y_{pg}\)の値も大きい
- \(\bar{x}_{\cdot g}\)の値が大きい集団ほど\(y_{pg}\)の値も大きい
という2つの効果が混ざっていることを意味します。 したがって,階層性を考慮したモデルで推定しない限り,\(\beta_1\)の効果を正しく解釈することは非常に難しいのです。
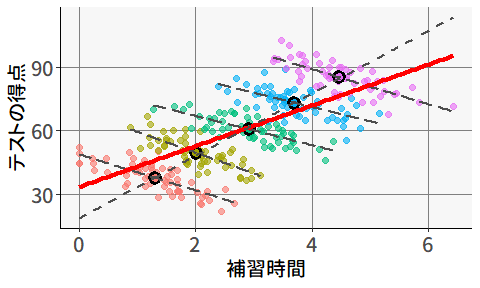
図 9.8 は,生態学的誤謬の例として示したプロットです。 集団(学校)ごとに求めた回帰係数は負の値となっている一方で,集団の平均値(黒丸)に基づいて求めた回帰直線は正の値となっていました。 ここでのポイントは,個人のデータレベルで求めた回帰直線(赤い線)が,集団ごとに求めた回帰直線と,集団平均に基づいて求めた回帰直線の傾きの中間になっているということです。 これこそが,「2つの効果が混ざっている」ことを示しています。
9.2 マルチレベル分析の出発点:分散分析
セクション 9.1.5 で見たように,階層性のあるデータの分析では,ある変数の値の変動を「集団レベル」と「個人レベル」のようにレベル毎に分解して考えます。 そのような分析の代表例として,(マルチレベルモデルなどは聞いたことがない人でもきっとご存知の)分散分析というものがあります。
分散分析自体の説明はここでは省略しますが,Rでは,aov()という関数によって,以下のように一要因の分散分析は簡単に実行可能です7。
分散分析では,「すべての集団の平均値が等しい」という帰無仮説を設定し統計的仮説検定を行います。 この際に使用する検定統計量\(F\)(F value,今回は21.38)は,簡単に言えば「集団レベルの変動( 図 9.7 の緑の矢印の長さ)」と「個人レベルの変動(オレンジ色の矢印の長さ)」の比に基づいており,集団レベルの変動が十分に大きければ「集団ごとに平均値が異なる」と判断しています。 したがって,とりあえずまずは分散分析を行えば,集団ごとに平均に差がある=データの階層性を考慮した分析手法を採用すべきか,が分かりそうな気がします。
このように,マルチレベル(階層線形)モデルは,分散分析を拡張したような形になっているのですが,実際にはもう少し考えなければいけないことがあります。 マルチレベルモデルの適用に際しては,集団ごとの変動に関する重要な考え方の違いを理解しておく必要があるのです。
9.2.1 固定効果と変量効果
分散分析が行っているのは,実際に観測された各学校の間に平均的な差があるかの検証です。 これは,各学校の差を詳細に検討したいような状況を想定しています(例:同じ市内の中学校の間に差があるか)。 したがって,分散分析から分かることは「そのデータの中にある学校間では平均値に差がある」ということです。
一方で,PISAデータの分析では,抽出された学校が具体的にどの学校であるかは問題ではありません。 たまたま無作為抽出でその学校が選ばれたからデータに含まれているだけで,何らかの理由でその学校が別の学校に変わったとしても,基本的には何も問題ないでしょう。 このように,一つ一つの集団には具体的な関心がなく,一般論としての「学校ごとの違い」などに関心があるような場合,分散分析では結果が「そのデータの中」に限定されてしまうため,別のアプローチのほうが良いと考えられます。 そこで,集団の平均値自体を確率変数とみなして,観測値はその実現値だと考えるのです。
このように,データの階層構造を考えるときには,レベル2以上の要素について「一つ一つの具体的な値に関心があるか」を明確に区別して考える必要があります。 具体的には,説明変数の効果は固定効果(fixed effects)と変量効果(random effects)のいずれかに分類されます。
固定効果(Fixed Effects)
固定効果とは,母集団の中で値が固定されている(決まっている)と見なされる効果のことです。 「固定」された値があると見なすならば,その値自体に関心があるわけで,そのために特定の集団を名指しで指定してデータを収集しているのです。 例えば,「性別による学力の差」を分析する場合,性別の効果は固定効果として扱います。 これは,男性と女性という2つのカテゴリが明確に定まっており,その効果の大きさ(回帰係数)が母集団全体で一定であると考えるためです。
各学校の平均値差を固定効果と見なして行う分散分析は,実は回帰分析の形で以下のように表すことができます。 \[ y_{pg} = \beta_0 + \beta_{02} x_{g=2} + \beta_{03} x_{g=3} + \cdots + \beta_{0G} x_{g=G} + u_{pg} \tag{9.4}\] ここで\(x_{g=g}\)は,その生徒が学校\(g\)に所属している場合は1をとり,それ以外では0となるダミー変数です。 したがって,上の式は集団\(g\)ごとに \[ \begin{alignedat}{3} y_{p1} &= \beta_0 &&+u_{p1} &&\quad (g=1) \\ y_{p2} &= \beta_0 +\beta_{02}&&+u_{p2} &&\quad (g=2) \\ y_{p3} &= \beta_0 +\beta_{03}&&+u_{p3} &&\quad (g=3) \\ &\vdots\\ y_{pG} &= \beta_0 +\beta_{0G}&&+u_{pG} &&\quad (g=G) \\ \end{alignedat} \tag{9.5}\] と書き分けることができます。 つまり,各ダミー変数に関する回帰係数\(\beta_{0g}~(g=2,3,\cdots,G)\)は,基準となる集団(上の式は\(g=1\))との平均値差を表している,と言えます。
そしてこのとき,分散分析の検定は,\(\beta_{0g}~(g=2,3,\cdots,G)\)がすべて0であるかを評価することと,数学的には同じことなのです。 実際に,school_idについてダミー変数化した回帰分析を行ってみましょう。 回帰分析を行うlm()関数では,説明変数が名義尺度(character型など)の場合,自動的にダミー変数化して分析を実行してくれます。
Call:
lm(formula = read_score ~ school_id, data = dat)
Residuals:
Min 1Q Median 3Q Max
-323.86 -49.34 0.37 50.13 275.00
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 621.2408 12.6256 49.205 < 2e-16 ***
school_id002 -148.3601 17.9861 -8.249 < 2e-16 ***
school_id003 -159.6712 18.9384 -8.431 < 2e-16 ***
school_id004 -115.5121 18.1239 -6.373 2.00e-10 ***
school_id005 -212.7595 18.4223 -11.549 < 2e-16 ***
school_id006 -9.3313 18.1239 -0.515 0.606669
[ reached 'max' / getOption("max.print") -- omitted 177 rows ]
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 74.69 on 5583 degrees of freedom
Multiple R-squared: 0.4107, Adjusted R-squared: 0.3915
F-statistic: 21.38 on 182 and 5583 DF, p-value: < 2.2e-16出力の(Intercept)は(9.4)式の\(\beta_0\),すなわちschool_id==001の学校の平均値を表しています。 そして,続くschool_id***は,それぞれの学校のschool_id==001との差を表しているわけです。 最も重要なポイントは,一番下に出力されている検定統計量(F-statistic)の値が,先程の分散分析のときと同じ(21.38)であるという点です。 これが,ダミー変数を用いた回帰分析と分散分析が数学的には等価であることを示しています。
平均値の違いを固定効果とみなした分析の結果は,例えば分散分析であれば「そのデータに含まれる学校の間には,平均値に差がある/ない」というものです。 したがって,この結果をもって「一般的に,世の中の学校(母集団全体)において平均値に差がどの程度あるか」までは分かりません(差があることくらいは分かったとしても)。 また,係数\(\beta_{0g}\)は,あくまでもその集団\(g\)ごとに個別に計算される値なので,複数の集団間の\(\beta_{0g}\)を比べるような分析,例えば「どのような特徴を持った集団ほど\(\beta_{0g}\)が大きい=平均値が高いのか」といった分析には不都合です8。
変量効果(Random Effects)
変量効果とは,母集団の中で確率的に変動する効果のことです。 これは先程説明したように,個々の集団の具体的な値はただの確率変数の実現値に過ぎず,再び同じようにランダムサンプリングを行えば異なる集団・異なる値になるだろう,と考えることを意味します。 PISAデータの例では,学校の効果は変量効果として扱います。 これは,データに含まれる具体的な学校(例:A高校,B高校)がたまたま抽出されただけであり,他の学校が抽出されても同様の分析を行いたいためです。
平均値の差を変量効果として扱う場合,もちろん「(特定の)A高校とB高校では具体的に平均値がどの程度(何点くらい)違うのか」を調べることには興味がありません。 代わりに「全体的に,学校ごとに平均値はどの程度のばらつきを持っているのか」を調べることになります。 このため数学的には,学校ごとの平均値差を変量効果として扱う場合,もはやパラメータ(\(\beta_{0g}\))でもないため表記を\(u_{pg}\)に変えて9, \[ u_{0g} \sim N(0, \sigma^2_{0g}) \tag{9.6}\] のように正規分布に従う確率変数であると仮定します。 このとき,分散分析のモデル式は(9.5)式とほぼ同じで良いのですが,少し変えて \[ y_{pg} = \mu +u_{0g} + u_{pg} \tag{9.7}\] となります。 なお,固定効果の場合の分散分析では,\(\beta_0\)は「集団\(g=1\)の平均値」を表していましたが,変量効果の場合の分散分析では,\(g=1\)も含めたすべての集団に対して付与される\(\beta_{0g}\)が平均0と仮定されている(9.6式)ため,パラメータ\(\mu\)はそのまま全体平均を表しています。
判断基準
ある要因を固定効果として扱うか変量効果として扱うかは,慣れないうちはなかなか悩むと思います。 基本的な判断の基準は,以下のような感じです。
固定効果として扱う場合:
- カテゴリ数が少ない
- 具体的なカテゴリの効果に関心がある(性差・地域差の比較など)
- カテゴリが理論的に意味を持つ(その学校を選んだことに必然性がある)
変量効果として扱う場合:
- カテゴリ数が多い
- 個々のカテゴリよりも変動の大きさに関心がある
- カテゴリ自体がランダムサンプリングされている(その学校である必要はない)
また,実用的な観点からは,サンプルサイズについても考慮する必要があります。 変量効果として扱うには,各レベルに十分なサンプルが必要です。 というのも,変量効果として扱う場合には,その変量効果のばらつき(\(\sigma^2_{0g}\))が推定の対象となるためです。 一般的には,レベル2のカテゴリ(例:学校)が30以上あることが推奨されます。 とはいえ,統計的な基準だけでなく,研究の理論的背景も考慮して決めなくてはいけません。 例えば,もしもリソースの都合によって,5つの学校からしかデータを集めることができなかったとしても,「一般的に学校ごとに差があるか」を評価したいのであれば,やはり(多少無理はあるにせよ)変量効果として分析するほうが良いかもしれません。
9.3 階層線形モデル
ここからは,集団ごとの違いを変量効果とみなした分析の実践に入っていきます。 まずは,最も基本的な回帰分析のマルチレベルモデルについて見ていきます。
9.3.1 ランダム切片モデル
階層線形モデル(Hierarchical Linear Model [HLM])の最も基本的なモデルは,先ほど説明した分散分析において,集団ごとの平均値差を変量効果に置き換えただけのモデルとされています。これを,ランダム切片モデル(random intercept model)と呼びます。 すでに部分的にはところどころで説明しているのですが,ここでまとめて,改めて「マルチレベルモデルの出発点」をおさえておきます。
これから紹介するモデルは,分野の慣習や,モデルのどの側面に注目するかによって,マルチレベルモデルや階層線形モデル以外にも異なる名称で呼ばれることがあります。
すべてのモデルには,必ず固定効果と変量効果が最低1つずつは含まれます。そのため混合効果モデル(mixed effects model)とも呼ばれることがあります。 とはいえ,やはりこのモデルのキモは変量効果にあり,そもそも回帰分析では固定効果がないモデルは存在しないことから,変量効果モデル(random effects model)やランダム係数モデルと(random coefficient model)いう名称もあります。
特に分野が異なる人と会話するときには,実は同じモデルを指しているのに,異なる名称で呼ばれている可能性があるので,まずはモデル式を見るようにすると良いかもしれません。
モデルの基本構造
ランダム切片モデルの最も基本的な形は,説明変数を含まない切片のみのモデル(null model または unconditional model)です。このモデルは,セクション 9.1.5 で説明した変動の分解の考え方を直接的に表現したものです。
数学的表現
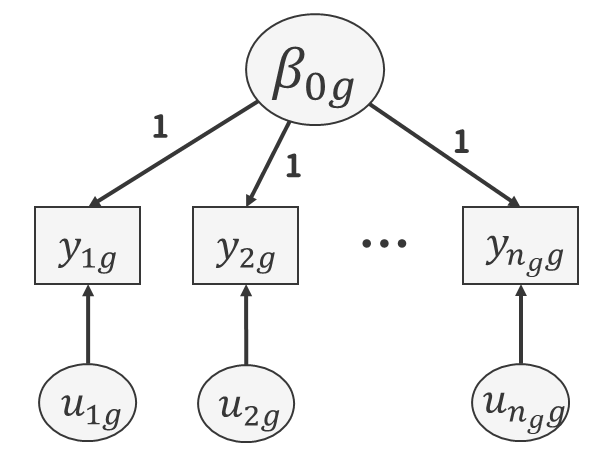
マルチレベルモデルでは,基本的に回帰式をレベルごとに作成することを考えます。 基本的なランダム切片モデルを表す場合には, \[ \begin{alignedat}{2} \text{(レベル1)} \quad & y_{pg} & & = \beta_{0g} + u_{pg} \\ \text{(レベル2)} \quad & \beta_{0g} & & = \mu + u_{0g} \end{alignedat} \tag{9.8}\] という要領です。 回帰式っぽく見えないかもしれませんが,これも立派な「説明変数のない回帰分析」の形です。 なお,式中の各項はそれぞれ
- \(y_{pg}\):第\(g\)集団の\(p\)番目の個人の従属変数の値
- \(\mu\):全体の平均
- \(u_{0g}\):第\(g\)集団の切片の全体平均との差
- \(u_{pg}\):個人レベルの誤差項(集団平均との差)
をそれぞれ表しています。 このモデルにおいて,\(u_{0g}\)および\(u_{pg}\)は変量効果に相当する項である一方,全体平均\(\mu\)は固定効果に相当します。 このように,階層線形モデルには必ず固定効果と変量効果が含まれています。
もちろん(9.8)の2つの式を組み合わせて, \[ y_{pg} = \mu + u_{0g} + u_{pg} \tag{9.9}\] のように表しても良いのですが,後ほど回帰分析の説明変数が追加されるときに,どちらのレベルの説明変数なのかを区別しやすいように,レベルごとに表記するのがおすすめです。
変量効果の仮定
変量効果と誤差項については,以下の仮定を置きます。 \[ \begin{aligned} u_{0g} &\sim N(0, \sigma^2_{0g}) \\ u_{pg} &\sim N(0, \sigma^2_{pg}) \\ \sigma_{u_{0g}, u_{pg}} &= 0 \end{aligned} \tag{9.10}\] 上2つの仮定は単に,集団レベル・個人レベルの変動を,それぞれ異なる正規分布に従う確率変数(変量効果)と見なすことを意味しています。 また,一番下の仮定は,集団レベルと個人レベルの変動が無相関であることを意味します。
以上の仮定のもとでは,\(y_{pg}\)の分布は \[ y_{pg} \sim N(\beta_{0g}, \sigma^2_{pg}) \tag{9.11}\] という形で表すことも可能であり,これが尤度関数を形作ります。 つまり,集団\(g\)に属する個人\(p\)の値\(y_{pg}\)は,集団\(g\)の平均\(\beta_{0g}\)を中心に,個人レベルの誤差項\(u_{pg}\)に従う正規分布に従うと考えるわけです。 これにより,各集団\(g\)の尤度関数は単純に正規分布の掛け算として表現されます。
モデルの意味
このモデルは,被説明変数の値の変動を, \[ y_{pg} = \overbrace{\mu}^{全体平均} + \overbrace{u_{0g}}^{集団平均と全体平均の差} + \overbrace{u_{pg}}^{個人値と集団平均の差} \tag{9.12}\] つまり,「全体平均」「集団効果」「個人効果」の3つの成分に分解したものです。 そして,(9.10)式の仮定のもとでは,被説明変数の総分散は以下のように分解されます。 \[ \sigma_{y}^2 = \sigma^2_{0g} + \sigma^2_{pg} \tag{9.13}\]
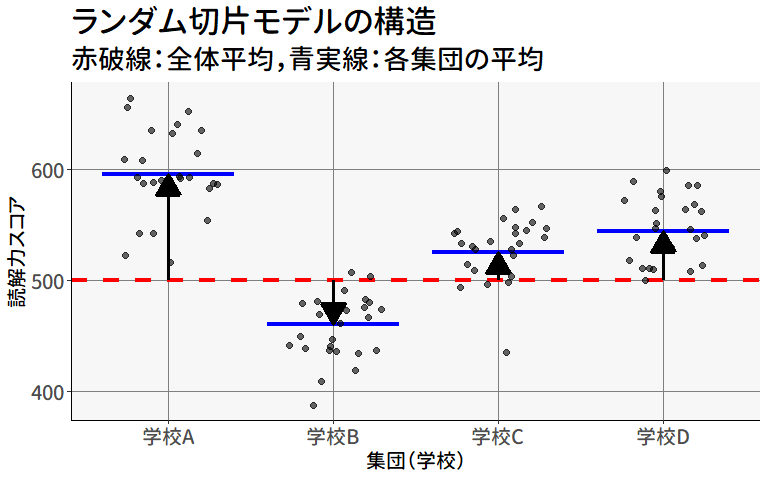
図 9.9 は,ランダム切片モデルのイメージ図です。 全体平均を表す赤い点線(\(\mu\))と,各グループの平均値(\(\beta_{0g}\))を表す青い実線の間の距離(矢印の長さ)が\(u_{0g}\)に相当し,この長さの母分散が\(\sigma^2_{0g}\)となります。
このモデルは,マルチレベル分析の出発点となる最も基本的なモデルです。 後ほど説明変数を追加していきますが,まずはこのモデルでデータの階層構造と変動の分解を理解しましょう。
Rでのランダム切片モデルの実装
Rでマルチレベルモデルを推定するには,パッケージと同名のglmmTMB()関数を使用します。
Family: gaussian ( identity )
Formula: read_score ~ (1 | school_id)
Data: dat
AIC BIC logLik -2*log(L) df.resid
66670.7 66690.7 -33332.3 66664.7 5763
Random effects:
Conditional model:
Groups Name Variance Std.Dev.
school_id (Intercept) 3624 60.2
Residual 5579 74.7
Number of obs: 5766, groups: school_id, 183
Dispersion estimate for gaussian family (sigma^2): 5.58e+03
Conditional model:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 503.699 4.562 110.4 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1glmmTMB()関数は,通常の回帰分析の関数lm()と似たような構文formulaを取ります。 ただし,固定効果と変量効果を明確に区別するために,少し特殊な記法を使用します。
通常の(school_idの効果を固定効果とした)lm()では,read_score ~ school_idと記述していました。 変量効果とする場合,この右辺のschool_idの部分を(1|school_id)に書き換えます。 このように,カッコの中の縦棒(|)の右側には,変量効果として扱う説明変数を書きます。 そして左側には,「レベル2の回帰分析の説明変数」を書きます(詳細は セクション 9.3.5 にて)。 とりあえず現時点では,そのような説明変数はまだ考えていないので,school_idによる変量効果の平均値(切片)を表す1だけを書いておきます。
lme4パッケージの場合の解説
上記の分析をlme4パッケージで実行する場合には,lmer()関数を使用します。 ただし引数は基本的にglmmTMB()関数と同じなので,パッケージを読み込んでいれば,関数名を変えるだけでOKです。
lme4)
Linear mixed model fit by maximum likelihood ['lmerMod']
Formula: read_score ~ (1 | school_id)
Data: dat
AIC BIC logLik -2*log(L) df.resid
66670.7 66690.7 -33332.3 66664.7 5763
Scaled residuals:
Min 1Q Median 3Q Max
-4.3531 -0.6575 0.0101 0.6729 3.6592
Random effects:
Groups Name Variance Std.Dev.
school_id (Intercept) 3624 60.2
Residual 5579 74.7
Number of obs: 5766, groups: school_id, 183
Fixed effects:
Estimate Std. Error t value
(Intercept) 503.699 4.562 110.4ただし,lmer()関数には,少し注意点があります。 まず,lmer()関数では少なくとも1つは変量効果が必ず含まれていないと実行できません。 したがって,間違えてschool_idを固定効果のように書いてしまった以下のコードではエラーとなります。 変量効果がないならば,素直にlm()を使っておけ,ということですね。
Error: No random effects terms specified in formulaなおglmmTMB()関数では,変量効果がない場合でも推定を行ってくれます(つまり通常のlm()関数も内包している)。
また,lmer()関数では,デフォルトで制限付き最尤法(REstricted Maximum Likelihood [REML])による推定が行われます。 細かい説明は省略するのですが,実は セクション 9.3.6 で説明するモデル比較においては,多くの場合でREML = FALSEとして通常の最尤法(ML)に変更しておかないと正しくない (川端,2019) ので,この引数の意味が分からなくても,こだわりが無ければ基本的にREML = FALSEをつけて実行するようにしてください。
なおglmmTMB()関数にも引数REMLは用意されているのですが,上述の理由からかデフォルトがfalseになっています。 したがって,glmmTMB()関数を使用する場合はREMLを明示的に使用したい場合だけ設定する必要があるということです。
改めて結果を見ると,Random effects:とConditional model:という形で,変量効果と固定効果が別々に記載されていることがわかります。
まず,Conditional model:には,固定効果として,ここではレベル2の回帰分析(9.8式)の結果が示されています。 といっても現時点では説明変数は何もないので,(Intercept)すなわち切片(全体平均)のみが示されています。 Estimateの503.699という値は,各集団の平均値(\(\beta_{0g}\))の期待値(\(\mu\))が503.699点,ということを意味します。 注意が必要な点として,これは個人レベルの全体平均の推定値とは異なる統計量です。 実際に,分析に使用しているデータについてread_scoreの平均値を計算すると,以下のようになります。
いま計算した個人レベルの標本平均は,集団のサンプルサイズの違いの影響を強く受けます。 極端な例を上げると,\(n_g=10000\)の学校1つと,\(n_g=10\)の学校99校のデータを混ぜた場合,個人レベルの標本平均は,ほぼ\(n_g=10000\)の学校の平均値によって決まるでしょう。 一方で,集団平均の期待値は,100校のデータをまんべんなく使用して算出されるべきです。 もちろんサンプルサイズの違いによって集団平均の推定精度が異なるため多少の重み付けは必要なのですが,このあたりをうまく調整した推定が行われるために,やや異なる値が得られるのです。
Random effects:には,変量効果の分散および標準偏差が示されています。 Groupsにはformulaのカッコ内の右側に書いた変数名(集団レベルの変数)が,Nameには左側に書いた変数名(レベル2の回帰分析の説明変数)が記されています。 したがって,school_id (Intercept)と記された行の値が,集団平均の分散(\(\sigma_{0g}^2\))および標準偏差を表しています。 同様に,Residualは残差を表しているので,これが個人レベルの分散(\(\sigma_{pg}^2\))および標準偏差を意味します。
以上の結果をランダム切片モデルの回帰式(9.8および9.10式)に代入すると, \[ \begin{alignedat}{3} \text{(レベル1)} \quad y_{pg} & = \beta_{0g} &&+ u_{pg}, &&\qquad u_{pg}\sim N(0, 74.7^2) \\ \text{(レベル2)} \quad \beta_{0g} & = 503.699 &&+ u_{0g}, &&\qquad u_{0g}\sim N(0, 60.2^2) \end{alignedat} \tag{9.14}\] という形になります。
なお,(9.13)式では,\(y_{pg}\)の総変動\(\sigma_y^2\)を2つの変量効果の分散の和に分解できると説明しました。 これも,全体平均\(\mu\)のときと同様に,観測された標本分散および不偏分散とは異なる値となります。 これは,データの階層構造を考慮しているか,そして計算方法の違いによって当然起こる違いです。
集団ごとの切片(\(\beta_{0g}\))は変量効果として扱われているため,モデルの中で直接推定されることはありません。 ただし,(制限付き)最尤法による推定の副産物として,事後的に各グループの切片(\(\beta_{0g}\))を計算することはできます。
coef()関数は,回帰係数を取得する関数ですが,glmmTMB()の結果に対しては,変量効果の平均値(切片)を集団ごとに計算してくれます。 この結果から,例えばschool_id == 001の学校の切片は616.2887と高く,この学校が相対的に他の学校よりも数学の学力が高いことなどがわかります。
9.3.2 階層性を考慮すべきか
ここまでに説明してきたランダム切片モデルがマルチレベルの出発点である理由は,このモデルによってそもそも階層性を考慮して分析する必要のあるデータなのかを検討できるためです。
社会科学におけるデータの多くには,何らかの形で階層性があると考えられます。 しかし,必ずしもその階層性を踏まえた分析を行わなくても良いケースもあります。 例えば,「数学の学力」を被説明変数とする場合にデータの階層性を意識する必要があるのは,「数学の学力」自体が学校ごとに平均的に異なると考えられるためです。 したがって,同じようにいくつかの学校から二段階抽出によってサンプリングされたデータであっても,例えば「運動の頻度」などの,学校(レベル2)よりは個人・家庭(レベル1)によって決まるような変数に関心がある場合には,わざわざマルチレベルモデルを使う必要は無いかもしれません10。 そこで,マルチレベルモデルの必要性をある程度統計的に判断するための具体的な基準を示します。
級内相関係数
セクション 9.1.5 で示した形で,変数の変動を「個人レベル」と「集団レベル」に分解すると,回帰係数に個人・集団レベルの効果が混ざること( 図 9.8 )や 標本平均の計算における二段階抽出の影響( 図 9.3 )は,総変動に占める集団レベルの変動の割合によって決まるということが見えてきます。
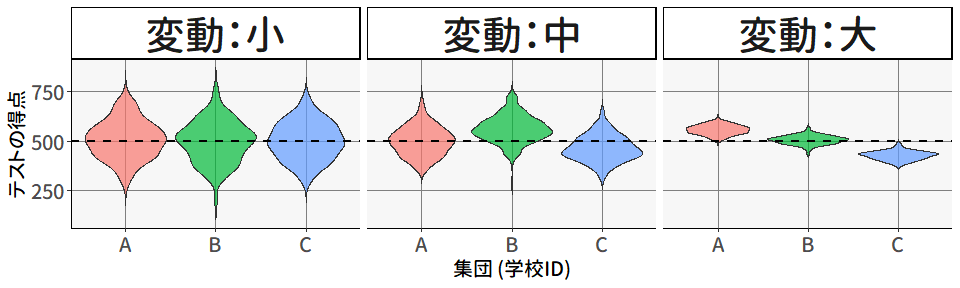
図 9.10 には,3つの学校からサンプリングされたテストの得点について,学校ごとに作成したバイオリンプロットが描かれています。 3つのプロットのいずれについても,3つの学校のデータをくっつけてテストの得点の分布を求めると,平均500,標準偏差100になるように設計されています。 図 9.7 にあるように,変動を分解して考えると,集団間の変動が大きいほど集団内の変動は小さくなります。
図 9.10 の左は,集団レベルの変動がほとんどないケースです。 この場合,各学校の平均値\(\bar{x}_{\cdot g}\)は,すべて全体平均\(\bar{x}\)と近い値になります。 そこで,\(\bar{x}_{\cdot g}=\bar{x}\)として(9.2)式を少し変形させると, \[ \begin{aligned} y_{pg}&= \mu &+& \beta_1[(x_{pg}-\bar{x}_{\cdot g})+\bar{x}_{\cdot g}] &+ u_{pg} \\ &=\mu &+& \beta_1[(x_{pg}-\bar{x})+\bar{x}] &+ u_{pg} \\ &=\mu + \beta_1\bar{x} &+& \beta_1(x_{pg}-\bar{x}) &+ u_{pg} \\ &= \mu^{*} &+& \beta_1(x_{pg}-\bar{x}) &+ u_{pg} \end{aligned} \tag{9.15}\] と書き換えることができます。 したがって,単純に説明変数を全体平均で中心化して切片を調整しただけの普通の回帰分析の形になることから,わざわざマルチレベルの分析を行う必要が無いことがわかります。
同様に,標本平均の計算(母平均の推定)を考えた場合も,集団ごとの違いが見られない場合は,仮に単一の学校からサンプリングを行ったとしても,あるいは学校にとらわれずに全体からランダムサンプリングしたとしても,同じような結果が得られると考えられます。 したがって,わざわざ階層性を考慮せずとも,普通に個人レベルで分析を行えば良いでしょう。
一方 図 9.10 の右は,集団レベルの変動が大きい場合です。 このときには,明らかに,\(\bar{x}_{\cdot g}=\bar{x}\)ではないことから,(9.15)式のように変換することはできず,結果として\(\beta_1\)には個人レベルと集団レベルの効果が混ざることになります。 したがって,マルチレベルの分析が必要となります。 これは,簡単に言えば\((x_{pg}-\bar{x})\)に対する回帰係数と\(\bar{x}\)に対する回帰係数を別々に設定して \[ y_{pg}= \beta_0 + \beta_{1}(x_{pg}-\bar{x}_{\cdot g})+\beta_{2}\bar{x}_{\cdot g} + \varepsilon_{pg} \] としてあげると良さそうです(詳細は後ほど)。 マルチレベルな分析の本質は,このように集団レベルの変数\(\bar{x}\)と個人レベルの変数\((x_{pg}-\bar{x})\)を同時に用いて,個別に効果を評価することにあると言えます。
以上に基づき,マルチレベルな分析手法を採用すべきかどうかを判断するための定量的な指標を,集団レベルの変動の割合に基づいて定義していきましょう。
(9.13)式に示されていたように,ランダム切片モデルのもとでは,ある変数\(y_{pg}\)の全体の分散は\(\sigma^2_{0g}+\sigma^2_{pg}\)と単純な和の形に分解することができました。 したがって,全体の変動に占める集団レベルの変動の割合は,単純に \[ \text{ICC} =\frac{\sigma^2_{0g}}{\sigma^2_{0g}+\sigma^2_{pg}} \tag{9.16}\] と定義できます。 この値のことを級内相関係数(inter-class correlation coefficient [ICC])と呼びます。 ICCがどの程度の大きさであればマルチレベルな分析が必要とされるかには諸説あるようですが,一説には
- ICC < 0.05: マルチレベルモデルの必要性は低い
- 0.05 ≤ ICC < 0.10: マルチレベルモデルを検討する価値がある
- ICC ≥ 0.10: マルチレベルモデルが強く推奨される
などと考えられているようです。
階層性を考慮した分析を行うべき理由は, 図 9.3 に示されていたように,二段階抽出を行うと,見かけのサンプルサイズよりも有効なサンプルサイズが小さいために,標準誤差が過小評価されてしまうことにありました。 これは,二段階抽出が行われると,サンプリングの効率が悪化してしまうことを意味しています。
このサンプリングの効率悪化の程度を示す指標として用いられることがあるのが,デザイン効果 (design effect)と呼ばれる指標です。 デザイン効果は \[ \text{Deff} = \frac{\text{二段階抽出における標準誤差}}{\text{無作為抽出における標準誤差}} \tag{9.17}\] と定義される値で,そのまま二段階抽出によってどれだけ推定の精度が悪化したかを表しています。 そして,このデザイン効果は,(9.16)式で定義されたICCを用いると, \[ \text{Deff} = 1 + (\bar{n_g}-1)\text{ICC} \tag{9.18}\] と表せることが知られています。 すなわち,ICCが大きいほどサンプリングの効率が悪化するのです。
そして一説によれば,Deffの値が2を超えてくると,マルチレベルな分析をしたほうが良いかも,と考えられたりするそうです。
RでICCの計算
ICCを計算するための材料は,すでにglmmTMB()関数によって出力されていました。 表示された値(\(\sigma_{0g}=60.2^2,~ \sigma_{pg}=74.7^2\))を用いて手計算しても良いのですが,よりシステマティックに,そして小数点以下の細かい値まで計算したい場合のために,関数を用いた計算方法も紹介しておきます。
performanceというパッケージには,回帰分析に関する様々な性能チェック(決定係数\(R^2\)やRMSEなどをはじめ,かなりいろいろな種類)の関数が用意されています。 その中にicc()という関数があり,これを使えば簡単に計算可能です。
performanceパッケージでICCの計算
今回のデータでは,ICCはおよそ0.394とかなり大きな値となりました。 したがって,マルチレベルな分析を行う必要性が高いと言えるでしょう。
以下の内容を書いたあとでperformanceパッケージの存在に気づいたのですが,performanceパッケージが使えなくなったときのためにこちら説明も残しておきます。
VarCorr()関数を使うと,推定された結果の中から分散成分のみを取り出すことができます。 あとは,頑張って各成分の数値を取り出せば,ICCが計算可能です。
きちんとperformance::icc()関数と(丸め誤差を除けば)同じ値が得られました。
ICCパッケージによるICCの計算について
ICCを計算するためのパッケージとして,実はICCというものも用意されています。
ICCという統計量自体は,マルチレベルモデル以外の文脈でも用いられるものです。 例えば,複数人が同じ人のパフォーマンスを採点するような場合,ICCが高いということは「採点者間で評価が一致している」とみなすことができます。 そのような用途でICCを計算することを想定しているので,ICCパッケージは,もともとマルチレベルモデルのために作られたものではないはずです。
実際にICCパッケージでは,(集団レベルの変動を固定効果とみなした)分散分析の考え方に基づいて,観測されたある変数の分散を「群間変動」と「群内変動」に分解してICCを求めます。 具体的には,「群間変動の総和(\(SS_B\))」と「群内変動(\(SS_W\))」をそれぞれの自由度で割った値をそれぞれ\(MS_{B},~MS_{W}\)と表したとき, \[
ICC=\frac{MS_B-MS_W}{MS_B + (n_g-1)MS_W}
\tag{9.19}\] という形で計算しています (McGraw & Wong, 1996, 細かい話は無視します)。 ICCest()関数は,ICCの点推定値および95%信頼区間を算出してくれる関数です。
Warning in ICCest(x = school_id, y = read_score, data = dat): 'x' has been
coerced to a factor結果を見ると,glmmTMB()の出力とはやや異なる値が出力されています。 これは,そもそものモデルの考え方が異なるためであり,マルチレベルモデルを実行すべきかを判断する,という意味では,glmmTMB()の出力に基づいて計算するほうが良いと考えられます。
ただし,もちろんICCest()にも使い所は色々とあります。 一つは,ランダム切片モデルにおけるICCのラフな見積もりとして,簡単に信頼区間まで計算してくれる,という点です。 そのため,説明変数のICCを計算する場合にはとりあえずICCest()を使うと良いかもしれません。
ここまでは被説明変数のICCを計算してきました。 というのも,そもそもマルチレベルな分析を行うのは,被説明変数の変動(分散)に関する集団レベル・個人レベルの要因を同時に考慮するためです。 一方でマルチレベルな分析では,個人レベルの変数と集団レベルの変数を同時に使用します。 したがって,例えば回帰分析を行う場合には,被説明変数だけでなく各説明変数についても,集団レベルの変数として扱うべきかを検討すると良いかもしれません。 このような目的の場合には,説明変数に関してもICCを計算してみると良いでしょう。
Warning in ICCest(x = school_id, y = escs, data = dat): 'x' has been
coerced to a factorescs(社会経済的地位)のICCがおよそ0.23であることから,これは学校ごとに平均が異なる変数と言えます。 したがって,説明変数として使用する場合には,集団レベルのESCS(集団の平均値)と個人レベルのESCSをそれぞれ異なる説明変数として使用することができそうです。
belong1)
Warning in ICCest(x = school_id, y = belong1, data = dat): 'x' has been
coerced to a factor所属感のICCはおよそ0.026と非常に低く,学校ごとに平均的に差があるとは言えなさそう(どの学校でも分布は概ね同じ)です。 したがって,この変数を説明変数として使用する場合には,集団レベルの変数として使う意味は薄く,個人レベルの変数として使用するのが良いでしょう。
9.3.3 変量効果として分析するメリット
ランダム切片モデルは,単に分散分析を変量効果に変更しただけのモデルです。 本来各集団の平均値には関心は無いのですが,計算すること自体は可能なので,先ほど紹介したcoef()関数を使って算出した集団平均(\(\beta_{0g}\))と,固定効果の分散分析の結果に基づく各学校の平均値(\(\beta_0 + \beta_{0g}\))を比較してみましょう。
# 固定効果の係数を取得
result_anova <- aov(read_score ~ school_id, data = dat)
intercept <- result_anova$coefficients[1]
# group1の平均はInterceptなので0を頭につける
group_diff <- c(0, result_anova$coefficients[-1])
coef_fixed <- intercept + group_diff
# 変量効果の係数を取得
coef_random <- coef(model0)$cond$school_id$`(Intercept)`
plot(coef_fixed, coef_random,
xlab = "固定効果の学校平均",
ylab = "変量効果の学校平均",
main = "固定効果と変量効果の比較"
)
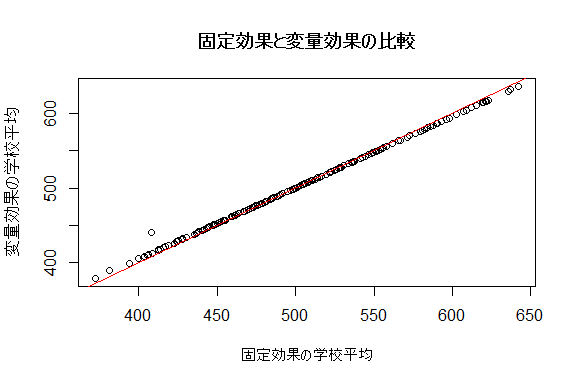
abline(a = 0, b = 1, col = "red") # y=xの直線を追加図 9.11 には,固定効果の分散分析の結果から得られた各学校の平均値と,ランダム切片モデルの結果から得られた各学校の平均値を比較した散布図が描かれています。 基本的にはほぼ同じ値になっているのですが,\(y=x\)の直線と比べると,わずかに傾きが小さくなっていることがわかります。 これは,変量効果の推定で行われている縮退推定(shrinkage estimation)を表したものです。
変量効果に関しては,その分布が何かしらの正規分布に従う(9.10式)と仮定していました。 したがって,変量効果の尤度の部分には,とりあえず全体平均\(\mu\)に近いほうが尤度が大きくなるという性質があります。 そして,ある集団の平均値\(\beta_{0g}=\mu+u_{0g}\)を推定する際,ざっくり言えば「変量効果の背後にある正規分布」と「その集団内のデータの尤度」の掛け算 \[ L(\mathbf{x}_{g}) = \overbrace{\prod_{p=1}^{n_g} f(x_{pg}|\beta_{0g},\sigma^2_{pg})}^{集団内のデータの尤度} \cdot \overbrace{\vphantom{\prod_{p=1}^{n_g}}f(\beta_{0g}|\mu,\sigma^2_{0g})}^{変量効果の尤度} \tag{9.20}\] を最大化するように求めています11。 したがって,変量効果として推定する際には,集団ごとの平均値を単にサンプリングした値として扱うのではなく,全体の平均に近づけるように調整された値が得られます。 そして,これは(9.20)式からわかるように,その集団のサンプルサイズ\(n_g\)が小さいほど,より強く全体平均に近づけられることになります。
この「縮退推定」が,結果的に集団平均の推定を真の値に近づけるのか遠ざけるのかは場合によります。 ただし,縮退推定は特にサンプルサイズが小さい集団がある場合には役に立つ可能性が高くなります。 例えば,ある学校(school_id == "001")では予算か何かの都合により\(n_g=3\)人しかサンプリングできなかったとします。
この場合,その学校の平均値は,たった3人のサンプルから計算されるため,その学校の真の平均値から大きく外れる可能性があります12。
もちろん固定効果の分散分析の場合には,この観測された平均値(734.5123)をそのまま学校の平均値として扱うことになります。
Call:
lm(formula = read_score ~ school_id, data = dat_use)
Residuals:
Min 1Q Median 3Q Max
-323.86 -49.15 0.35 49.89 275.00
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 734.51 43.13 17.028 < 2e-16 ***
school_id002 -261.63 45.00 -5.814 6.42e-09 ***
school_id003 -272.94 45.39 -6.014 1.93e-09 ***
[ reached 'max' / getOption("max.print") -- omitted 180 rows ]
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 74.71 on 5551 degrees of freedom
Multiple R-squared: 0.4085, Adjusted R-squared: 0.3891
F-statistic: 21.07 on 182 and 5551 DF, p-value: < 2.2e-16しかしこのとき,ランダム切片モデルを用いて集団平均を推定すると,どうなるでしょうか。
このように,ランダム切片モデルを用いると,集団平均の推定値は(変量効果として)全体平均に近づいた値になるのです。 イメージとしては,サンプルサイズが小さい集団の平均値が他の集団から著しく離れている場合に,「他の集団の平均値から考えると,そんなに異常な値ということはないだろう」という感じで調整をしていると言えます。
したがって,変量効果を用いることで,集団ごとの平均値の推定がより安定する可能性があるのです。 試しに,
school_id == "001"の学校からランダムに3人をサンプリングする- 他の学校のデータはすべて使用する
- ダミー変数を用いた回帰分析とランダム切片モデルでそれぞれパラメータを推定する
- この操作を100回繰り返して,散布図を描く
というシミュレーションをしてみました。
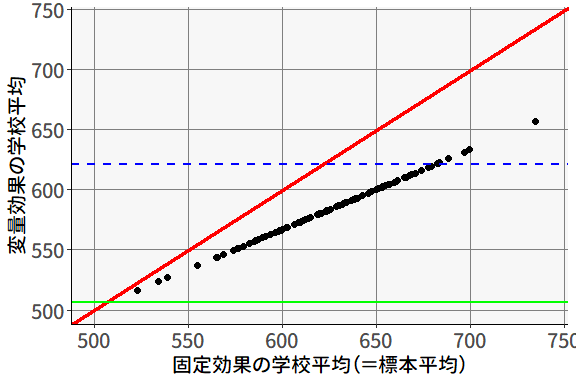
図 9.12 を見ると,すべての点が赤い直線(\(y=x\))よりも下にあります。 school_id == "001"の学校はもともと優秀な学校なので,どの3人を選んでも全体平均以下になることはないのですが,それでもランダム切片モデルを用いると,その学校の平均値は全体平均(緑の実線あたり)に近づくように調整されていることが分かります。 その結果,ランダム切片モデルでは,\(n_g=3\)の割に,集団平均の推定値のばらつきが小さくなっています。 これが,変量効果として分析する直接的なメリットの一つなのです。
なお,図 9.12 の青い点線は,school_id == "001"の学校の全体平均(母集団平均)を表しています。 つまり本来サンプルサイズが十分に大きければこの値に収束するはずなのですが,縮退推定では,この「本来の平均値」に近づくわけではなく,他の集団も含めた全体の平均値(緑の実線)に近づいていきます。 したがって,school_id == "001"の学校のように,もともと全体平均から離れた集団において,サンプリングが逆方向に偏ってしまった場合には,むしろその集団の本来の平均値から更に離れてしまうこともあり得るという点は注意が必要です。
9.3.4 説明変数を含むランダム切片モデル
ランダム切片モデルによってICCがそれなりに大きい値になることが分かったら,次は回帰分析のように説明変数を含むモデルに拡張していきましょう。 ここでは,まず「社会経済的地位(ESCS)が高い生徒ほど読解力が高いのか」を検証する回帰モデルを考えてみます。 まずシンプルに説明変数を追加することを考えると, \[ y_{pg} = \mu + \beta_{\mathrm{ESCS}}\mathrm{ESCS}_{pg} + u_{0g} + u_{pg} \tag{9.21}\] という形になります。 ESCSは個人ごとに異なる値をとる(個人レベルの変数である)ため,上の式をレベルごとに表すならば \[ \begin{alignedat}{2} \text{(レベル1)} \quad & y_{pg} & & = \beta_{0g} +\beta_{\mathrm{ESCS}}\mathrm{ESCS}_{pg} + u_{pg} \\ \text{(レベル2)} \quad & \beta_{0g} & & = \mu + u_{0g} \end{alignedat} \tag{9.22}\] と表記できます。
このモデルは,glmmTMB()関数を使うと以下のように実装可能です。 単純に説明変数を追加するだけであれば,lm()関数のときと同じようにformulaの右辺に変数名を書くだけです。
Family: gaussian ( identity )
Formula: read_score ~ escs + (1 | school_id)
Data: dat
AIC BIC logLik -2*log(L) df.resid
66636.0 66662.6 -33314.0 66628.0 5762
Random effects:
Conditional model:
Groups Name Variance Std.Dev.
school_id (Intercept) 3313 57.56
Residual 5558 74.56
Number of obs: 5766, groups: school_id, 183
Dispersion estimate for gaussian family (sigma^2): 5.56e+03
Conditional model:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 504.791 4.375 115.38 < 2e-16 ***
escs 9.478 1.564 6.06 1.36e-09 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1出力のConditional model:のところを見ると,escsの推定値が9.478となっています。 したがって,「escsが高い生徒ほど,read_scoreの値も高い」と言えそうです。
lme4パッケージは検定をしてくれない
実は変量効果がある場合には,検定に必要な自由度の正確な定義が難しく,どうやらlme4パッケージの作者の思想として,不正確な可能性があるくらいなら表示しない,というスタンスを取っているようです。 そうは言ってもやはり固定効果の検定の結果が欲しい場面はあるでしょう。 lmer()の結果に対して検定結果(\(p\)値)を出してほしい場合には,lmerTestというパッケージをロードしてからlmer()関数を実行するだけです。
lme4)
Linear mixed model fit by maximum likelihood . t-tests use
Satterthwaite's method [lmerModLmerTest]
Formula: read_score ~ escs + (1 | school_id)
Data: dat
AIC BIC logLik -2*log(L) df.resid
66636.0 66662.6 -33314.0 66628.0 5762
Scaled residuals:
Min 1Q Median 3Q Max
-4.3224 -0.6498 0.0124 0.6705 3.6257
Random effects:
Groups Name Variance Std.Dev.
school_id (Intercept) 3313 57.56
Residual 5558 74.56
Number of obs: 5766, groups: school_id, 183
Fixed effects:
Estimate Std. Error df t value Pr(>|t|)
(Intercept) 504.791 4.375 179.861 115.388 < 2e-16 ***
escs 9.478 1.549 5724.542 6.117 1.02e-09 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Correlation of Fixed Effects:
(Intr)
escs 0.040 lmerTestパッケージは,lme4::lmer()関数の出力に対して,近似的に計算された自由度を用いて\(p\)値を表示してくれるようになります。 「じゃあ最初からlmerTestパッケージを使えばいいじゃないか」と思われるかもしれません。 正直それでも良いと思います。 そしてglmmTMB()パッケージはデフォルトで検定結果を出してくれます。 ただし,2つの関数で算出される標準誤差(Std. Error)の値が異なるので,どうやら自由度の定義が異なっているようです。
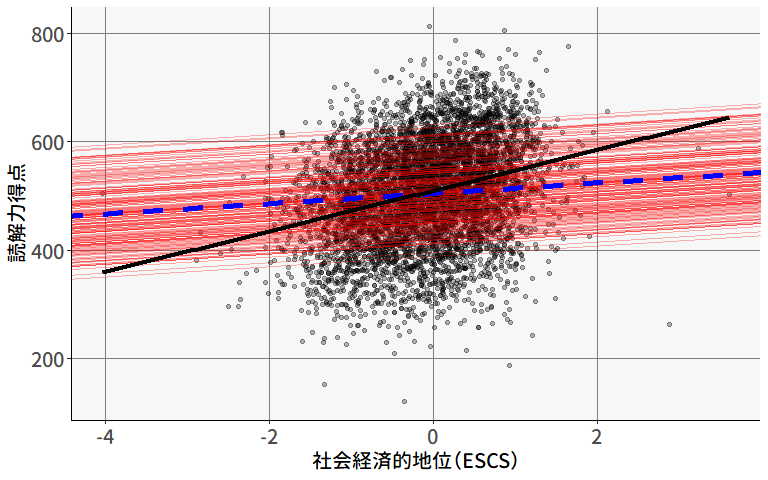
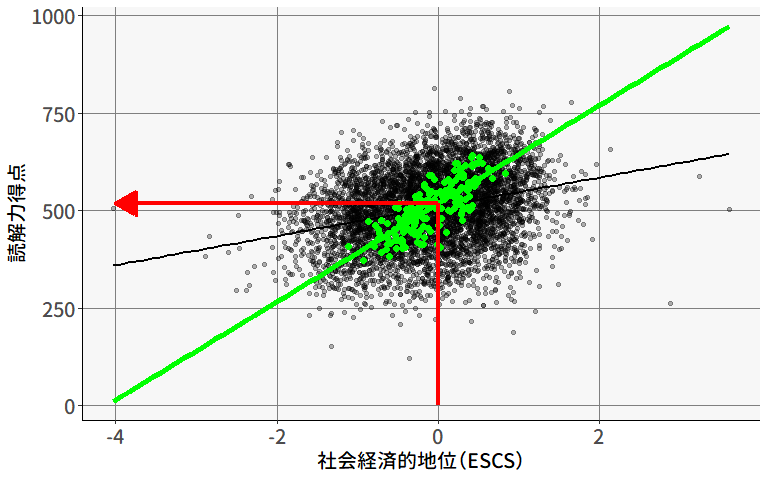
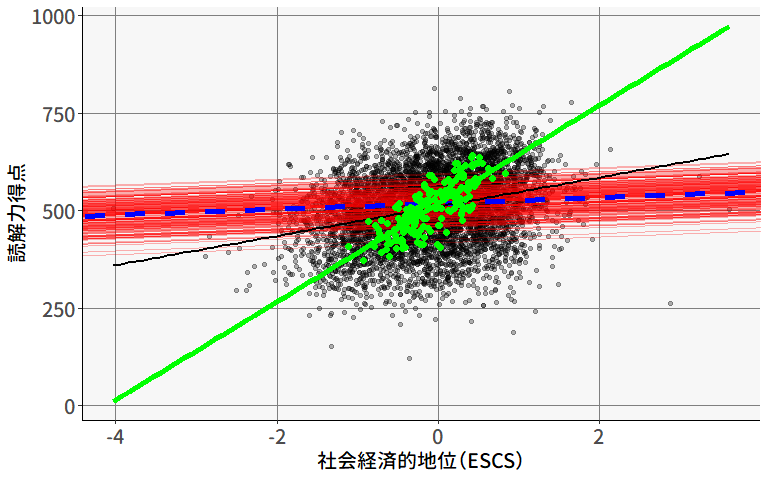
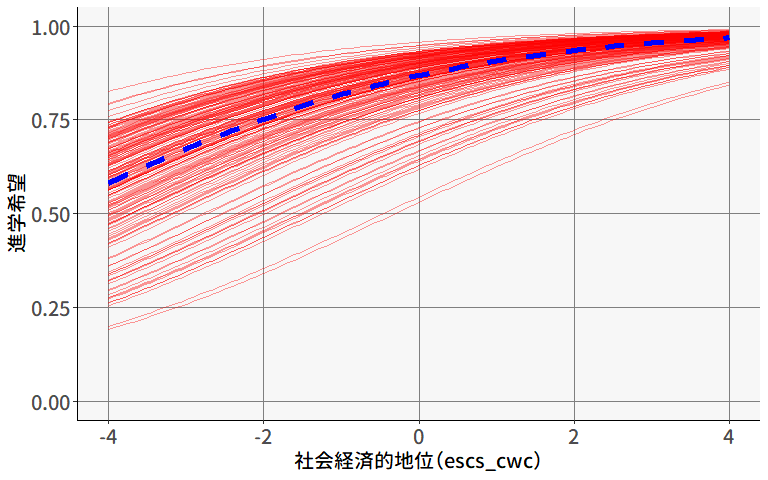
ということで,得られた推定値を(9.22)式に代入すると, \[ \begin{alignedat}{3} \text{(レベル1)} \quad & y_{pg} &&= \beta_{0g} +9.478\mathrm{ESCS}_{pg} + u_{pg}, &\quad& u_{pg} \sim N(0, 74.56^2) \\ \text{(レベル2)} \quad & \beta_{0g} &&= 504.791 + u_{0g}, &\quad& u_{0g} \sim N(0, 57.56^2) \end{alignedat} \tag{9.23}\] となります。 図 9.13 は,このモデルを可視化したものです。 青い点線は切片の全体平均(\(\mu\))に基づいて引いた回帰直線を,また赤い実線は各集団(学校)の\(\beta_{0g}\)の推定値に基づいて引いた回帰直線を表しています。 (9.22)式に示されているように,ランダム切片モデルでは傾き\(\beta_{\mathrm{ESCS}}\)はすべての集団で同じ値となっています。
また,黒い実線は切片の変量効果を含めない通常の回帰分析によって得られる回帰直線です。 ランダム切片モデルにおける回帰直線の傾きと比べると,わずかに傾きが大きいことが分かります。 これは,ランダム切片モデルでは集団レベルの効果が多少は変量効果(\(u_{0g}\))の方に分離されていることを示しています。
改めてこのモデルの回帰係数\(\beta_{\mathrm{ESCS}}\)が意味するところを考えてみると, セクション 9.1.5 で見たように,これは集団レベルの効果と個人レベルの効果が混ざったものになっています(9.2式)。 すなわち,
- \((\mathrm{ESCS}_{pg}-\overline{\mathrm{ESCS}}_{\cdot g})\)の値が大きい,すなわち集団内で相対的に値が大きい個人ほど\(y_{pg}\)の値も大きい
- \(\overline{\mathrm{ESCS}}_{\cdot g}\)の値が大きい集団ほど\(y_{pg}\)の値も大きい
という2つの効果が混ざった値になっているのです。 このままでは,「ESCSが読解力に与える効果」の解釈は非常にややこしくなってしまいます。 このような場合には,説明変数を個人レベルと集団レベルに分解するのが良いでしょう。
集団レベルの説明変数を含むランダム切片モデル
まずは,集団レベルの説明変数を含むモデルを考えてみます。 これは,先ほど見たように,ESCSの集団平均である\(\overline{\mathrm{ESCS}}_{\cdot g}\)を代わりに使用するだけです。 \[ y_{pg} = \mu +\beta_{\overline{\mathrm{ESCS}}}\overline{\mathrm{ESCS}}_{\cdot g}+ u_{0g} + u_{pg} \tag{9.24}\] この場合,\(\overline{\mathrm{ESCS}}_{\cdot g}\)は集団内では同じ値をとる(集団レベルの変数である)ため,上の式をレベルごとに表すならば \[ \begin{alignedat}{2} \text{(レベル1)} \quad & y_{pg} & & = \beta_{0g} + u_{pg} \\ \text{(レベル2)} \quad & \beta_{0g} & & = \mu +\beta_{\overline{\mathrm{ESCS}}}\overline{\mathrm{ESCS}}_{\cdot g} + u_{0g} \end{alignedat} \tag{9.25}\] と表記されます。
今回のデータには,たまたまescsの集団平均がsch_escs_mean列に入っていたので,これを使いましょう。
Family: gaussian ( identity )
Formula: read_score ~ sch_escs_mean + (1 | school_id)
Data: dat
AIC BIC logLik -2*log(L) df.resid
66518.6 66545.3 -33255.3 66510.6 5762
Random effects:
Conditional model:
Groups Name Variance Std.Dev.
school_id (Intercept) 1461 38.22
Residual 5579 74.69
Number of obs: 5766, groups: school_id, 183
Dispersion estimate for gaussian family (sigma^2): 5.58e+03
Conditional model:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 518.060 3.131 165.44 <2e-16 ***
sch_escs_mean 126.570 8.153 15.52 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1得られた係数を(9.25)式に代入すると, \[ \begin{alignedat}{3} \text{(レベル1)} \quad & y_{pg} && = \beta_{0g} + u_{pg}, &\quad& u_{pg}\sim N(0, 74.69^2) \\ \text{(レベル2)} \quad & \beta_{0g} && = 518.060 +126.570\overline{\mathrm{ESCS}}_{\cdot g} + u_{0g}, &\quad& u_{0g} \sim N(0, 38.22^2) \end{alignedat} \tag{9.26}\] となります。
そんなわけで,マルチレベルモデルを使用する場合には集団レベルの平均値の計算を行うことが多々あります。 わかりやすい方法としては,dplyrパッケージのgroup_by()関数を利用する方法です。
あるいは,Rにデフォルトで入っているave()関数もシンプルに使いやすい関数です。 この関数は,指定した変数の値でグループを作成し,そのグループごとに平均値を計算してくれます。
[1] 0.466865714 0.466865714 0.466865714 0.466865714 0.466865714
[6] 0.466865714 0.466865714 0.466865714 0.466865714 0.466865714
[11] 0.466865714 0.466865714 0.466865714 0.466865714 0.466865714
[16] 0.466865714 0.466865714 0.466865714 0.466865714 0.466865714
[21] 0.466865714 0.466865714 0.466865714 0.466865714 0.466865714
[26] 0.466865714 0.466865714 0.466865714 0.466865714 0.466865714
[31] 0.466865714 0.466865714 0.466865714 0.466865714 0.466865714
[36] -0.386726471 -0.386726471 -0.386726471 -0.386726471 -0.386726471
[41] -0.386726471 -0.386726471 -0.386726471 -0.386726471 -0.386726471
[46] -0.386726471 -0.386726471 -0.386726471 -0.386726471 -0.386726471
[51] -0.386726471 -0.386726471 -0.386726471 -0.386726471 -0.386726471
[56] -0.386726471 -0.386726471 -0.386726471 -0.386726471 -0.386726471
[61] -0.386726471 -0.386726471 -0.386726471 -0.386726471 -0.386726471
[66] -0.386726471 -0.386726471 -0.386726471 -0.386726471 -0.003253571
[71] -0.003253571 -0.003253571 -0.003253571 -0.003253571 -0.003253571
[76] -0.003253571 -0.003253571 -0.003253571 -0.003253571 -0.003253571
[81] -0.003253571 -0.003253571 -0.003253571 -0.003253571 -0.003253571
[86] -0.003253571 -0.003253571 -0.003253571 -0.003253571 -0.003253571
[91] -0.003253571 -0.003253571 -0.003253571 -0.003253571 -0.003253571
[96] -0.003253571 -0.003253571 -0.490621212 -0.490621212 -0.490621212
[ reached 'max' / getOption("max.print") -- omitted 5666 entries ]あるいは別の方法として,これもRにデフォルトで入っているaggregate()関数を使うのも一つの手です。
aggregate()
ここで,集団レベルの説明変数を含むランダム切片モデルの特徴を視覚的に確認してみましょう。 図 9.14 には,集団ごとの平均値を緑の点で示し,これに基づいて求めた回帰直線を緑の実線で示しています。 この回帰直線の切片および傾きは,先ほど求めたConditional model:に示された値と一致しています。
この緑の回帰直線は,各集団の切片(\(\beta_{0g}\))の予測値を表しており,例えばESCSの集団平均が0の学校の切片は,おおよそ518.060くらいになるだろう,ということを表します。
また,もとのescsを説明変数に入れた通常の回帰分析における回帰直線が黒い実線で示されています。 これと比べると,明らかに回帰係数が大きくなっていることが分かります13。
いま実行したモデルによって得られる回帰係数\(\beta_{\overline{\mathrm{ESCS}}}\)は,「生徒の平均的なESCSが高い学校ほど,読解力の平均値が高いか」を表しています。 すなわち,この分析は学校間の切片の違いが何によって説明できるのかを明らかにできるわけです。 しかし,このままでは個人レベルの効果,つまり「ESCSが高い生徒ほど…」と言えるかは全くわかりません。
個人レベルの説明変数も加えたランダム切片モデル
(9.2)式で見たように,個人と集団の両レベルの効果を含んだ説明変数\(x_{pg}\)を分解する場合には, \[ x_{pg} = (x_{pg} - \bar{x}_{\cdot g}) + \bar{x}_{\cdot g}, \tag{9.27}\] すなわち集団レベルの変数として平均値\(\bar{x}_{\cdot g}\),そして個人レベルの変数として集団平均を引いた値\(x_{pg}-\bar{x}_{\cdot g}\)に分解する必要があります。 このように,レベル1の変数をモデルに含める際には,集団平均中心化(centering within cluster [CWC])という操作が非常に重要となります。
そして,集団平均中心化した説明変数を加えることで,モデル式は \[ y_{pg} = \mu +\beta_{\mathrm{ESCS}}(\mathrm{ESCS}_{pg}-\overline{\mathrm{ESCS}}_{\cdot g})+\beta_{\overline{\mathrm{ESCS}}}\overline{\mathrm{ESCS}}_{\cdot g}+ u_{0g} + u_{pg} \tag{9.28}\] となり,レベルごとに表すならば \[ \begin{alignedat}{2} \text{(レベル1)} \quad & y_{pg} & & = \beta_{0g} +\beta_{\mathrm{ESCS}}(\mathrm{ESCS}_{pg}-\overline{\mathrm{ESCS}}_{\cdot g})+ u_{pg} \\ \text{(レベル2)} \quad & \beta_{0g} & & = \mu +\beta_{\overline{\mathrm{ESCS}}}\overline{\mathrm{ESCS}}_{\cdot g} + u_{0g} \end{alignedat} \tag{9.29}\] と表記されます。 セクション 9.3.4 の最初のモデル(9.21式)との違いとして,本来単一の説明変数を,中心化を挟むことで2つのレベルの説明変数に分解し,それぞれに異なる回帰係数を推定するというのが重要なポイントです。
集団平均中心化した説明変数を作成するのは,集団平均が先に用意されているならば簡単です。
こうして作成された「集団平均中心化後の説明変数」の値escs_cwcは,「その集団(学校)の中で相対的にESCSがどの程度高い/低いか」を表す値となっています。
それでは,集団平均中心化した変数と集団平均を同時にモデルに含めて分析してみましょう。
Family: gaussian ( identity )
Formula: read_score ~ escs_cwc + sch_escs_mean + (1 | school_id)
Data: dat
AIC BIC logLik -2*log(L) df.resid
66498.0 66531.3 -33244.0 66488.0 5761
Random effects:
Conditional model:
Groups Name Variance Std.Dev.
school_id (Intercept) 1461 38.23
Residual 5557 74.54
Number of obs: 5766, groups: school_id, 183
Dispersion estimate for gaussian family (sigma^2): 5.56e+03
Conditional model:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 518.060 3.132 165.43 < 2e-16 ***
escs_cwc 7.446 1.563 4.77 1.88e-06 ***
sch_escs_mean 126.569 8.153 15.53 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1集団レベルの効果の推定値(Conditional model:)は先程とほぼ同じ126.569になっています。 この点は変わらないまま,集団平均中心化した説明変数を加えたことで,ESCSのもたらす個人レベル・集団レベルの両方の効果が評価できるようになりました。
得られた係数を(9.29)式に代入すると, \[ \begin{alignedat}{3} \text{(レベル1)} \quad & y_{pg} & & = \beta_{0g} +7.446(\mathrm{ESCS}_{pg}-\overline{\mathrm{ESCS}}_{\cdot g})+ u_{pg}, &\quad& u_{pg} \sim N(0, 74.54^2) \\ \text{(レベル2)} \quad & \beta_{0g} & & = 518.060 +126.569\overline{\mathrm{ESCS}}_{\cdot g} + u_{0g}, &\quad& u_{0g} \sim N(0, 38.23^2) \end{alignedat} \tag{9.30}\] となります。
ここまでの分析の集大成となるモデルについて,結果を可視化してみましょう。
図 9.15 には,
- 青い点線: 切片の全体平均(\(\mu\))に基づいて引いた回帰直線
- 赤い線: 各集団(学校)の\(\beta_{0g}\)の推定値に基づいて引いた回帰直線
- 緑の線: 各学校の集団平均(ESCS)と読解力得点の平均値(緑の点)に基づいて引いた回帰直線
- 黒い線: 集団平均中心化した説明変数を含めない通常の回帰分析によって得られる回帰直線
がそれぞれ描かれています。 したがって,青い点線の傾きが「(集団内の)個人レベルの効果の大きさ」を,緑の線の傾きが「集団レベルの効果の大きさ」を,それぞれ表しています。
実質的な意味
2つのレベルに分解した説明変数を加えたランダム切片モデルによって,ESCSが読解力に及ぼす効果の大きさが分かりました。 推定値はそれぞれ,集団レベルの回帰係数が126.568,個人レベルの回帰係数が7.446でした。 この結果をまとめると,以下のようなことが言えます。
- 集団内効果:同じ学校内でも社会経済的地位が高い生徒ほど読解力得点が高い
- 集団間効果:社会経済的地位が高い生徒が多い学校ほど,その学校の生徒全体の読解力得点が高い
- 効果の大きさの比較:多くの場合,集団間効果の方が集団内効果よりも大きくなる傾向がある
特に3点目は,説明変数(escs)を個人レベルと集団レベルに分解したとしてもそのスケールは変わらないことから,これらの係数を直接比較可能と見なして得られる知見です。 とはいえ,本当に個人レベルの効果と集団レベルの効果の大きさを直接比較することに意味があるかはまた別の話です。
いずれにしても,これは教育社会学における重要な知見であり,学校の文脈効果(同じ能力の生徒でも,どの学校に通うかによって成果が変わる)を示したものと言えます。
変動の説明
マルチレベルモデルに限らず,回帰分析では分散説明率が重要な指標となります。 そこで,分散説明率に相当するものとして,これまでに実行してきたモデルについて,ランダム切片やレベル1,2の説明変数を入れたことで,それぞれのレベルの変動のうちどの程度の割合が説明されたか(分散説明率: proportion of variance explained [PVE])を確認してみましょう。
まずは,各モデルの分散成分を取得する関数を定義します。
models <- list(model0, model1, model2, model3)
model_names <- c("model0", "model1", "model2", "model3")
model_var <- c(
"(Intercept)", # model0
"escs", # model1
"mean", # model2
"cwc + mean" # model3
)
# 分散成分の取得
get_variance_components <- function(model) {
vc <- VarCorr(model)$cond # 分散だけ取り出す
school_var <- as.numeric(vc$school_id[1]) # 集団レベルの分散
residual_var <- attr(vc, "sc")^2 # 個人レベル(残差)の分散
return(c(school_var = school_var, residual_var = residual_var))
}そして,これを各モデルに適用して,分散成分を比較してみましょう。
# sapply()関数を使って,先ほど作成したmodelsリストの各要素に適用する
variance_table <- data.frame(
Model = model_names,
var = model_var,
t(sapply(models, get_variance_components))
)
# 変動の減少率を計算
# 集団レベルの総変動
baseline_school_var <- variance_table$school_var[1]
# 個人レベルの総変動
baseline_residual_var <- variance_table$residual_var[1]
# 集団レベルについてどれだけ変動が減少したか
variance_table$PVE_school <-
(baseline_school_var - variance_table$school_var) / baseline_school_var
# 個人レベルについてどれだけ変動が減少したか
variance_table$PVE_residual <-
(baseline_residual_var - variance_table$residual_var) / baseline_residual_var
print(variance_table)個人レベルの回帰係数(\(\beta_{\mathrm{ESCS}}\))があまり大きな値ではなかったことからも示唆されるように,今回のデータにおいてESCSは,個人レベルの変動にはほとんど寄与していない(どのモデルについてもPVE_residualがほぼゼロである)ことが分かります。 一方で,集団レベルのPVEは大きな値(model2, 3ではPVE_schoolが0.6程度)となっており,集団レベルの変動の説明変数として重要な役割を果たしていることが分かります。 このように,分散説明率PVEは,通常の回帰分析と同じように,ある説明変数を(場合によってはどちらのレベルに)投入すべきかを判断するのに役に立つ指標となります。
さらなる集団レベル変数の追加
もちろんモデルは更に拡張可能です。 例えば,レベル2の説明変数を追加することで,集団レベルの変数が平均値に及ぼす影響をさらに考慮することができます。 ここでは,既にデータに含まれているST比(生徒教員比)も集団レベルの変数として追加してみましょう。 これは,少人数学級のほうが生徒の学力が高いのか,という仮説を検証するようなイメージです。
この場合,レベル2の説明変数が追加されるので,モデル式は \[ y_{pg} = \mu +\beta_{\mathrm{ESCS}}(\mathrm{ESCS}_{pg}-\overline{\mathrm{ESCS}}_{\cdot g})+\beta_{\overline{\mathrm{ESCS}}}\overline{\mathrm{ESCS}}_{\cdot g} + \beta_{\mathrm{ST}}\mathrm{ST}_{\cdot g}+ u_{0g} + u_{pg} \tag{9.31}\] となり,レベルごとに表すならば \[ \begin{alignedat}{2} \text{(レベル1)} \quad & y_{pg} & & = \beta_{0g} +\beta_{\mathrm{ESCS}}(\mathrm{ESCS}_{pg}-\overline{\mathrm{ESCS}}_{\cdot g})+ u_{pg} \\ \text{(レベル2)} \quad & \beta_{0g} & & = \mu +\beta_{\overline{\mathrm{ESCS}}}\overline{\mathrm{ESCS}}_{\cdot g} + \beta_{\mathrm{ST}}\mathrm{ST}_{\cdot g}+ u_{0g} \end{alignedat} \tag{9.32}\] と表記されます。
Family: gaussian ( identity )
Formula:
read_score ~ escs_cwc + sch_escs_mean + s_t_ratio + (1 | school_id)
Data: dat
AIC BIC logLik -2*log(L) df.resid
66494.9 66534.9 -33241.5 66482.9 5760
Random effects:
Conditional model:
Groups Name Variance Std.Dev.
school_id (Intercept) 1416 37.63
Residual 5557 74.54
Number of obs: 5766, groups: school_id, 183
Dispersion estimate for gaussian family (sigma^2): 5.56e+03
Conditional model:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 500.0671 8.5274 58.64 < 2e-16 ***
escs_cwc 7.4461 1.5625 4.77 1.88e-06 ***
sch_escs_mean 122.4814 8.2412 14.86 < 2e-16 ***
s_t_ratio 1.4621 0.6458 2.26 0.0236 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1得られた係数を(9.33)式に代入すると, \[ \begin{alignedat}{3} \text{(レベル1)} \quad & y_{pg} & & = \beta_{0g} +7.4461(\mathrm{ESCS}_{pg}-\overline{\mathrm{ESCS}}_{\cdot g})+ u_{pg}, &\quad& u_{pg} \sim N(0, 74.54^2) \\ \text{(レベル2)} \quad & \beta_{0g} & & = 500.0671 +122.4814\overline{\mathrm{ESCS}}_{\cdot g} + 1.4621\mathrm{ST}_{\cdot g}+ u_{0g}, &\quad& u_{0g} \sim N(0, 37.63^2) \end{alignedat} \tag{9.33}\] となります。
結果を見ると,s_t_ratioの係数は正となっていることから,どうやらむしろST比の高い学校のほうが生徒の読解力がやや高い傾向があるようです。 ただこの結果が少人数教育を否定するものであるかは分かりません。 一応集団レベルにはすでにsch_escs_meanが含まれているため,この効果は統制された偏回帰係数として算出されて入るのですが,ESCSに含まれない別の要因が影響している可能性は否定できないためです。
9.3.5 ランダム切片・傾きモデル
これまでに紹介してきたランダム切片モデルはいずれも,レベル1説明変数(escsあるいはescs_cwc)の回帰係数は集団ごとに同じ値となっていました。 しかし,場合によっては集団ごとに回帰係数が異なることもあります。 例えば,レベル1説明変数として「勉強時間」を考えた場合,「正しい勉強のしかた」を教えてくれる学校では勉強時間の効果が大きい一方で,そうでない学校では勉強時間が学力にあまり結びつかない(回帰係数が小さい)可能性もあるでしょう。 またESCSについても,私立学校ではそもそものESCSのばらつきが小さいために回帰係数が小さい一方で,公立学校ではESCSのばらつきが大きく,回帰係数も大きい可能性が考えられます。
このような場合には,傾きが集団ごとに異なることを許容した拡張であるランダム傾きモデル(random slopes model)を使用します。 なお,ICCの計算で見たように,マルチレベルモデルの基本は集団間の切片の差に起因します。 そのためランダム傾きモデルも,ほとんどの場合にはランダム切片も同時に適用する,ランダム切片モデルの拡張と位置づけられます。
傾きを固定効果とみなすモデル
本題に入る前に,まずは傾きを固定効果とみなすモデルを考えてみましょう。 これは,個人レベルの説明変数をそのままモデルに入れる通常の回帰分析と同じです。 ただし,分散分析のダミー変数と同じように,傾きを集団の数だけ設定する必要があります。 したがって,モデル式としては \[
y_{pg} = \beta_0 + \beta_{\mathrm{ESCS}}\mathrm{ESCS}_{pg}+\overbrace{(\beta_{0g}+ \beta_{\mathrm{ESCS},g}\mathrm{ESCS}_{pg})x_{g=g} + \cdots}^{G-1\text{個だけ足す}} + u_{pg}
\tag{9.34}\] となります。 これだとわかりにくいので,再び集団\(g\)ごとに分解すると, \[
\begin{aligned}
y_{p1} &= \beta_{0} \hspace{-.5em}&+ &\beta_{\mathrm{ESCS}}\mathrm{ESCS}_{p1} \hspace{-.5em}&+ &u_{p1} \hspace{-.5em}& \quad (g=1) \\
y_{p2} &= \beta_{0} + \beta_{02} \hspace{-.5em}&+ &(\beta_{\mathrm{ESCS}}+\beta_{\mathrm{ESCS},2})\mathrm{ESCS}_{p2} \hspace{-.5em}&+ &u_{p2} \hspace{-.5em}& \quad (g=2) \\
y_{p3} &= \beta_{0} + \beta_{03} \hspace{-.5em}&+ &(\beta_{\mathrm{ESCS}}+\beta_{\mathrm{ESCS},3})\mathrm{ESCS}_{p3} \hspace{-.5em}&+ &u_{p3} \hspace{-.5em}& \quad (g=3) \\
& \vdots \\
y_{pG} &= \beta_{0} + \beta_{0G} \hspace{-.5em}&+ &(\beta_{\mathrm{ESCS}}+\beta_{\mathrm{ESCS},G})\mathrm{ESCS}_{pG} \hspace{-.5em}&+ &u_{pG} \hspace{-.5em}& \quad (g=G)
\end{aligned}
\tag{9.35}\] という要領で,(9.5)式と同じように,集団ごとに切片と傾きそれぞれについて「\(g=1\)との違い」の係数を設定することに相当します。 このモデルは,lm()関数を使えば以下のように実行可能です。
(前略)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.170e+02 1.657e+01 37.234 < 2e-16 ***
school_id002 -1.458e+02 2.225e+01 -6.554 6.13e-11 ***
school_id003 -1.552e+02 2.172e+01 -7.149 9.91e-13 ***
school_id004 -1.075e+02 2.266e+01 -4.744 2.15e-06 ***
(中略)
school_id185 -1.484e+02 2.295e+01 -6.468 1.08e-10 ***
escs 9.096e+00 2.317e+01 0.393 0.694693
school_id002:escs -1.346e+01 3.043e+01 -0.442 0.658330
school_id003:escs 4.823e+01 2.779e+01 1.736 0.082693 .
school_id004:escs -1.421e+00 2.890e+01 -0.049 0.960792
(後略)この結果から,例えばschool_idが001,002の学校の回帰直線はそれぞれおよそ \[
\begin{alignedat}{4}
\text{(学校1)} &\quad y_{p1} &&= 617.0 &&+ 9.096\mathrm{ESCS}_{p1} &&+ u_{p1} \\
\text{(学校2)} &\quad y_{p2} &&= (617.0 - 145.8) &&+ (9.096 - 13.46)\mathrm{ESCS}_{p2} &&+ u_{p2} \\
& &&= 471.2 &&- 4.364\mathrm{ESCS}_{p2} &&+ u_{p2}
\end{alignedat}
\tag{9.36}\] という要領で,具体的に各集団ごとの回帰直線を個別に求めることができます。
しかし,このモデルは集団ごとに傾きを設定するため,集団の数だけ回帰係数が必要となり,集団の数が多い場合には非常に多くのパラメータを推定することになります。 また,集団の数が多い場合には,その解釈は非常に大変になってしまうでしょう。 ということで,紹介はしましたが,集団の数が多い場合にはこのモデルはあまり実用的ではありません。
基本的なランダム傾きモデル
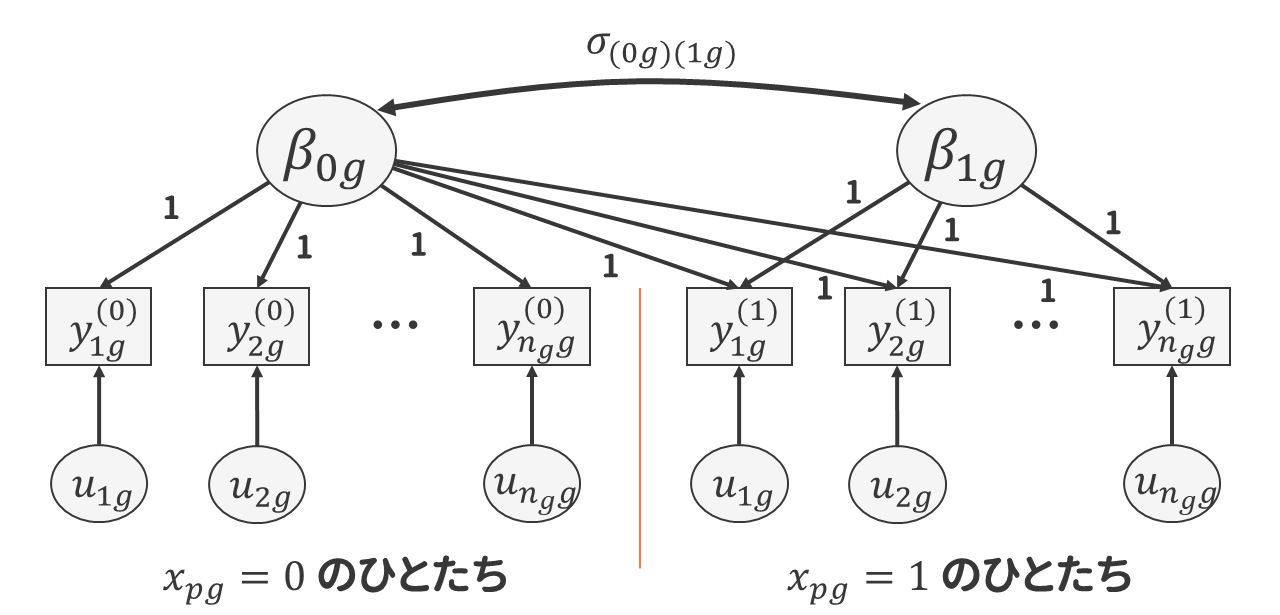
ということで,個人レベルの説明変数の傾きを変量効果とみなすランダム傾きモデルを考えてみましょう。 考え方は今までと同じで,集団ごとに異なる傾き\(\beta_{\mathrm{ESCS},g}\)を何かしらの正規分布に従う確率変数と考えるだけです。 \[ \begin{alignedat}{2} \text{(レベル1)} \quad & y_{pg} & & = \beta_{0g} +\beta_{\mathrm{ESCS},g}(\mathrm{ESCS}_{pg}-\overline{\mathrm{ESCS}}_{\cdot g})+ u_{pg} \\ \text{(レベル2)} \quad & \beta_{0g} & & = \mu_0 + u_{0g}\\ \text{(レベル2)} \quad & \beta_{\mathrm{ESCS},g} & & = \mu_{\mathrm{ESCS}} + u_{\mathrm{ESCS},g} \end{alignedat} \tag{9.37}\] 変量効果が複数になる場合には,それぞれの変量効果に対して,レベル2の回帰式が設定されることになります。 これは,後ほど「切片の説明変数」と「傾きの説明変数」がそれぞれ投入されるときに,しっかりと区別するうえで重要な書き方です。
このとき,それぞれの変量効果に対して,以下の仮定を置きます。 \[
\begin{alignedat}{2}
\text{(レベル1)} &u_{pg} &&\sim N(0, \sigma^2_{pg}) \\
\text{(レベル2)} &\left[\begin{array}{c}
u_{0g} \\ u_{\mathrm{ESCS},g}
\end{array}\right] &&\sim MVN\left(
\left[\begin{array}{c}
0 \\ 0
\end{array}\right],
\left[\begin{array}{cc}
\sigma_{0g}^2 & \sigma_{(0g)(\mathrm{ESCS},g)} \\
\sigma_{(0g)(\mathrm{ESCS},g)} & \sigma_{\mathrm{ESCS},g}^2
\end{array}\right]\right)
\end{alignedat}
\tag{9.38}\] これまでと同様に,基本的に各変量効果は正規分布に従い,また異なるレベル間の変量効果は相関しないと仮定します。 ただし,同じレベルの変量効果(今回で言えば\(u_{0g}\)と\(u_{\mathrm{ESCS},g}\))には多変量正規分布\(MVN(\boldsymbol{\mu}, \boldsymbol{\Sigma})\)を仮定します。 簡単に言えば,これは同じレベルの変量効果の間には相関関係を認める,ということです。 その具体的な意味は後ほど確認するとして,まずはglmmTMB()関数でこのモデルを実行してみましょう。
傾きに変量効果を持たせるためには,まず普通にその説明変数をformulaの右辺に入れます。 これによって,「傾きの全体平均(\(\mu_{\mathrm{ESCS}}\))」を推定できるようになります。
Family: gaussian ( identity )
Formula: read_score ~ escs_cwc + (escs_cwc | school_id)
Data: dat
AIC BIC logLik -2*log(L) df.resid
66648.6 66688.6 -33318.3 66636.6 5760
Random effects:
Conditional model:
Groups Name Variance Std.Dev. Corr
school_id (Intercept) 3626.8 60.22
escs_cwc 106.9 10.34 -0.09
Residual 5512.9 74.25
Number of obs: 5766, groups: school_id, 183
Dispersion estimate for gaussian family (sigma^2): 5.51e+03
Conditional model:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 503.695 4.563 110.40 < 2e-16 ***
escs_cwc 7.396 1.751 4.22 2.4e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1傾きの変量効果の情報は,出力のRandom effects:の部分に記載されています。 Groupsがschool_idでNameがescs_cwcとなっている行が,傾きの変量効果に関する情報です。 また,一番右にはCorrという列が追加されています。 これは,変量効果の相関係数 \[
\rho_{(0g)(\mathrm{ESCS},g)} = \frac{\sigma_{(0g)(\mathrm{ESCS},g)}}{\sqrt{\sigma_{0g}^2} \sqrt{\sigma_{\mathrm{ESCS},g}^2}}
\tag{9.39}\] を表しています。 したがって,得られた係数を(9.37)式に代入すると, \[
\begin{alignedat}{2}
\text{(レベル1)} \quad & y_{pg} & & = \beta_{0g} +\beta_{\mathrm{ESCS},g}(\mathrm{ESCS}_{pg}-\overline{\mathrm{ESCS}}_{\cdot g})+ u_{pg} \\
\text{(レベル2)} \quad & \beta_{0g} & & = 503.695 + u_{0g}\\
\text{(レベル2)} \quad & \beta_{\mathrm{ESCS},g} & & = 7.396 + u_{\mathrm{ESCS},g}
\end{alignedat}
\tag{9.40}\] また変量効果は \[
\begin{alignedat}{2}
\text{(レベル1)} &u_{pg} &&\sim N(0, 74.25^2) \\
\text{(レベル2)} &\left[\begin{array}{c}
u_{0g} \\ u_{\mathrm{ESCS},g}
\end{array}\right] &&\sim MVN\left(
\left[\begin{array}{c}
0 \\ 0
\end{array}\right],
\left[\begin{array}{cc}
60.22^2 & -56.05 \\
-56.05 & 10.34^2
\end{array}\right]\right)
\end{alignedat}
\tag{9.41}\] となります14。
固定効果escs_cwcの値が正であることから,個人レベルの効果は,平均的には正の値を持つことが分かります。 ただし,その変量効果の標準偏差が10.34と大きな値であることから,集団ごとに傾きが大きく異なり,場合によっては負の値になりうることも見えてきます。 実際に,データに含まれている集団(学校)ごとの係数を見てみましょう。
(Intercept) escs_cwc
001 616.3353 6.187427
002 474.2600 5.242309
003 463.3115 23.355328
004 505.6372 7.446572
005 413.0458 4.324954
006 607.0751 8.663129
007 584.1511 7.371261
008 416.7438 10.494779
009 503.3077 6.174089
010 379.0714 10.940293
[ reached 'max' / getOption("max.print") -- omitted 173 rows ]最初の10校には傾きが負になっている学校はありませんでしたが,係数が大きいところでは20を超えている一方で1桁の学校も多く,確かに学校ごとに傾きが大きく異なっていることが分かります。
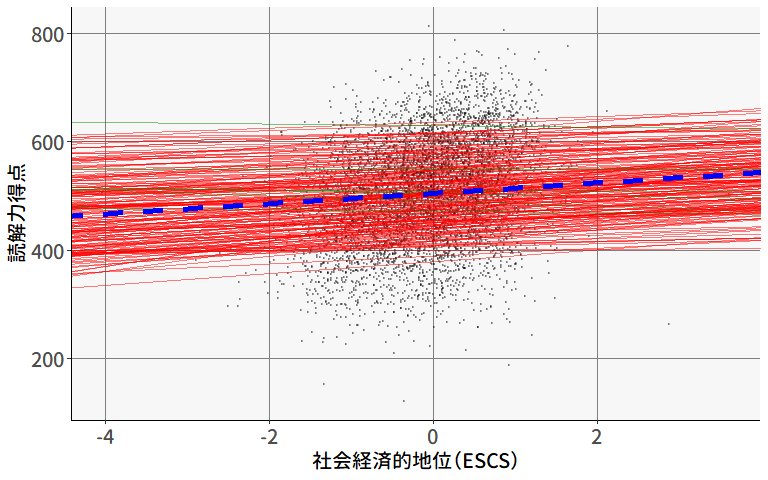
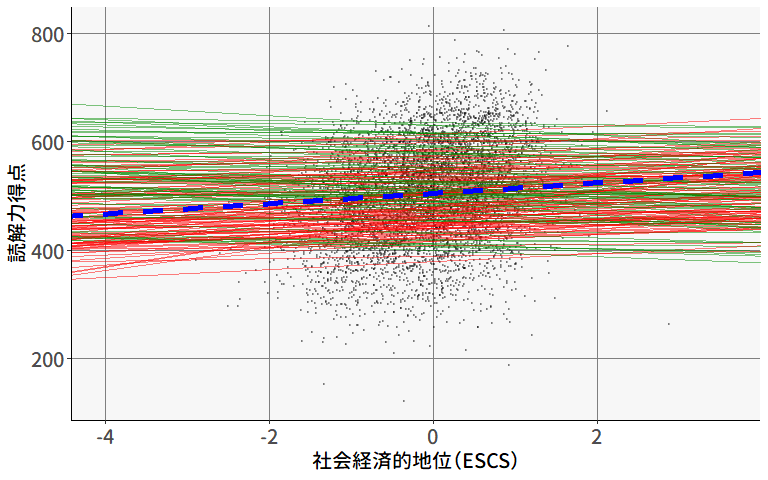
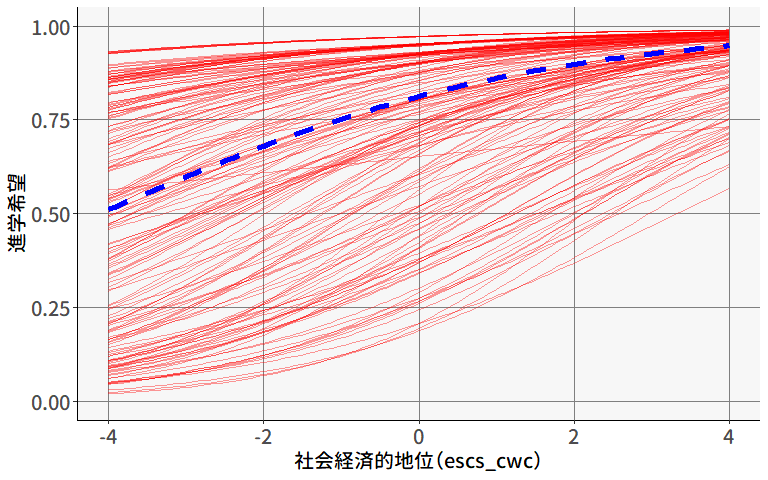
図 9.16 は,集団ごとの傾きの変量効果を視覚化したものです。 read_scoreの値のスケールが大きいのでやや分かりにくいですが,集団ごとに求めた回帰直線は,確かに傾きが微妙に異なっているようです。 試しに,傾きが正の場合は赤,負の場合は緑で色分けしてみると,一部の集団では傾きが負の値になっていることが分かります。
formulaに固定効果を入れ忘れてしまうと
そろそろ分かってきたかもしれませんが,glmmTMB()関数(やlmer()関数)のformulaでは,カッコに入れない説明変数は固定効果(すべての集団で共通の係数)を表し,カッコの中にある説明変数が変量効果を表します。 そのため,傾きの変量効果を推定する場合には,ほとんど全ての場合において,カッコの中と外にそれぞれ同じ説明変数を指定する必要があるのです。
これを忘れてしまうと,モデルとしては以下のようになります。 \[
\begin{alignedat}{2}
\text{(レベル1)} \quad & y_{pg} & & = \beta_{0g} +\beta_{\mathrm{ESCS},g}(\mathrm{ESCS}_{pg}-\overline{\mathrm{ESCS}}_{\cdot g})+ u_{pg} \\
\text{(レベル2)} \quad & \beta_{0g} & & = \mu + u_{0g}\\
\text{(レベル2)} \quad & \beta_{\mathrm{ESCS},g} & & = u_{\mathrm{ESCS},g}
\end{alignedat}
\tag{9.42}\] つまり,各集団の傾き\(\beta_{\mathrm{ESCS},g}\)は,全体平均が0になるように推定されてしまうのです。 もちろん,事前に「傾きの全体平均は0である」という確固たる信念や自負や証拠があるならば,このように設定しても問題ありません。 むしろ推定するパラメータを1つ減らすことができるので良いかもしれません。 しかし,ほとんどの場合ではそのようなことが事前に分かっていることはないでしょう。 ということで,基本的には常にformulaの右辺に説明変数を2回書くことを忘れないようにしましょう。
以下は,実際に固定効果に指定するのを忘れて実行してしまった場合の結果です。
Family: gaussian ( identity )
Formula: read_score ~ (escs_cwc | school_id)
Data: dat
AIC BIC logLik -2*log(L) df.resid
66663.7 66697.0 -33326.8 66653.7 5761
Random effects:
Conditional model:
Groups Name Variance Std.Dev. Corr
school_id (Intercept) 3627.8 60.23
escs_cwc 157.6 12.56 -0.12
Residual 5514.4 74.26
Number of obs: 5766, groups: school_id, 183
Dispersion estimate for gaussian family (sigma^2): 5.51e+03
Conditional model:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 504.812 4.774 105.7 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 escs_cwc (Intercept)
001 -0.1697830 616.3282
002 -0.6870569 474.2846
003 23.4385752 463.1085
004 2.6156933 505.6190
005 -1.3208036 413.0862
006 2.9982828 607.0461
007 2.0129289 584.1247
008 6.2975992 416.7272
009 0.5201487 503.3150
010 7.3494200 379.0455
[ reached 'max' / getOption("max.print") -- omitted 173 rows ]実際に回帰直線を引いてみると, 図 9.16 よりも緑の線(負の傾きになる集団)の割合が大きいことが分かります。
ちなみに,切片(1)に関しては,説明変数が1つでもある場合には,特に除外の指定をしない限り自動的に固定効果にも変量効果にも含まれるため,わざわざ書かなくても問題ありません。
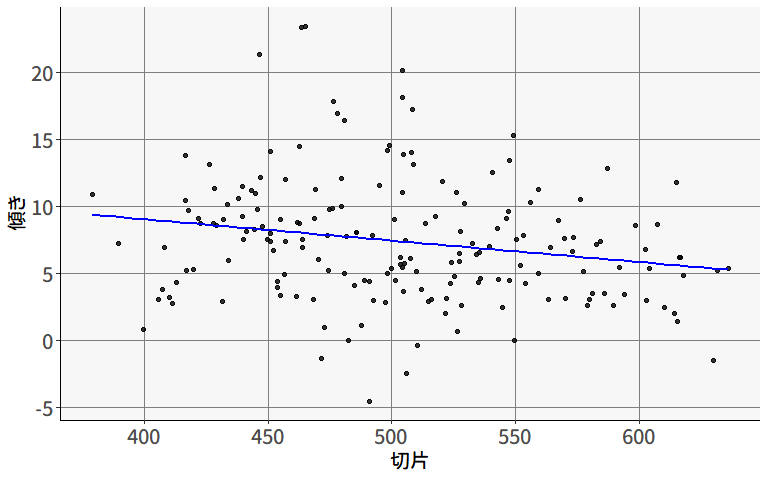
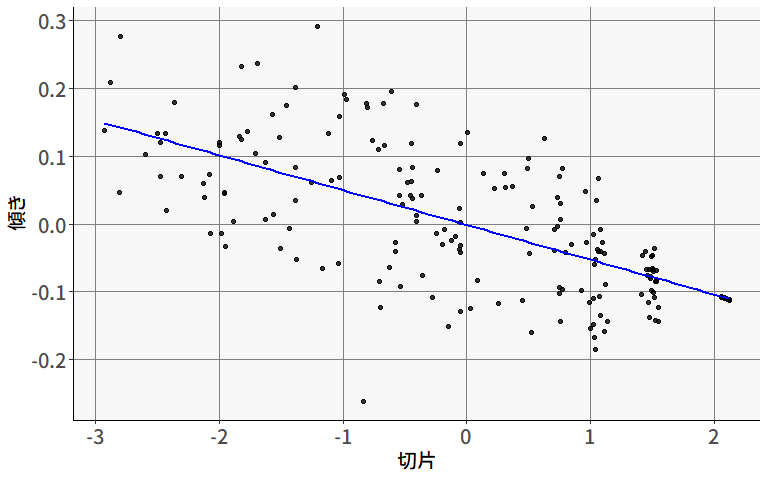
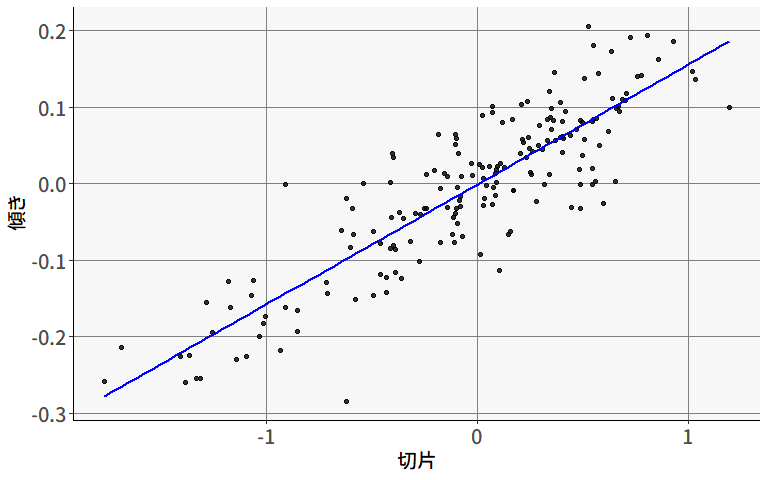
続いて,集団レベルの変量効果間の相関係数が負の値になっていることの意味を確認してみましょう。 一言で言えば,これは切片が大きい集団ほど,escs_cwcがread_scoreに与える正の効果が小さくなっていくことを意味します。 図 9.18 は,切片と傾きの変量効果の散布図です。
このような負の相関が生じるメカニズムまではさすがにこの結果からは分かりませんが,想像すると以下のような現象などが考えられそうです。
- 切片が大きい=学力が高い学校は,もともと入試の時点である程度選抜されているために,生徒のESCSのばらつきが小さく,ESCSの効果が小さくなる。
- 切片が小さい=学力が高くない集団は,入試での選抜が相対的に強くないために,個人レベルのESCSの効果がまだ残っている。
これ以上の議論は領域の専門家に任せるとして,とりあえずはこのような解釈が可能になりそうな分析ができました。
説明変数を含むランダム切片モデル
ランダム切片モデルでは,escs_cwcの傾きが集団(学校)ごとに異なることを確認しました。 そうすると,次は「傾きの差異の原因は何か」を明らかにしたくなるものです。 図 9.18 では,事後的に推定された傾きと切片の散布図に対して回帰直線を引いて,負の関係を示しました。 続いては,この関係をモデル式の中に組み込んでいきましょう。 ということで,切片と傾きの両方に対して,\(\mathrm{ESCS}_{pg}\)の集団平均である\(\overline{\mathrm{ESCS}}_{\cdot g}\)を説明変数として投入します。 \[
\begin{alignedat}{2}
\text{(レベル1)} \quad & y_{pg} & & = \beta_{0g} +\beta_{\mathrm{ESCS},g}(\mathrm{ESCS}_{pg}-\overline{\mathrm{ESCS}}_{\cdot g})+ u_{pg} \\
\text{(レベル2)} \quad & \beta_{0g} & & = \mu + \beta_{0,\overline{\mathrm{ESCS}}}\overline{\mathrm{ESCS}}_{\cdot g} + u_{0g}\\
\text{(レベル2)} \quad & \beta_{\mathrm{ESCS},g} & & = \beta_{\mathrm{ESCS}} +\beta_{1,\overline{\mathrm{ESCS}}}\overline{\mathrm{ESCS}}_{\cdot g} + u_{\mathrm{ESCS},g}
\end{alignedat}
\tag{9.43}\]
このモデルには,合計3つの固定効果が含まれています:
- \(\beta_{0,\overline{\mathrm{ESCS}}}\):切片の集団平均に対する効果
- \(\beta_{\mathrm{ESCS}}\):傾きの全体平均
- \(\beta_{1,\overline{\mathrm{ESCS}}}\):傾きの集団平均に対する効果
そして,それぞれの固定効果に対応する説明変数を考えるために,3つの式を1つにまとめてみると, \[ \begin{alignedat}{1} y_{pg} &=\beta_{0g} +\beta_{\mathrm{ESCS},g}(\mathrm{ESCS}_{pg}-\overline{\mathrm{ESCS}}_{\cdot g})+ u_{pg} \\ &= (\mu + \beta_{0,\overline{\mathrm{ESCS}}}\overline{\mathrm{ESCS}}_{\cdot g} + u_{0g}) + (\beta_{\mathrm{ESCS}} + \beta_{1,\overline{\mathrm{ESCS}}}\overline{\mathrm{ESCS}}_{\cdot g} + u_{\mathrm{ESCS},g})(\mathrm{ESCS}_{pg} - \overline{\mathrm{ESCS}}_{\cdot g}) + u_{pg} \\ &= \mu + \beta_{0,\overline{\mathrm{ESCS}}}\underbrace{\overline{\mathrm{ESCS}}_{\cdot g}}_{集団レベル} + \beta_{\mathrm{ESCS}}\underbrace{(\mathrm{ESCS}_{pg} - \overline{\mathrm{ESCS}}_{\cdot g})}_{個人レベル} + \beta_{1,\overline{\mathrm{ESCS}}}\underbrace{\overline{\mathrm{ESCS}}_{\cdot g}(\mathrm{ESCS}_{pg} - \overline{\mathrm{ESCS}}_{\cdot g})}_{交互作用} \\ &+ \underbrace{u_{0g} + u_{\mathrm{ESCS},g}(\mathrm{ESCS}_{pg} - \overline{\mathrm{ESCS}}_{\cdot g}) + u_{pg}}_{変量効果} \\ \end{alignedat} \tag{9.44}\] という形になっています。 すなわち,個人レベルの説明変数\((\mathrm{ESCS}_{pg} - \overline{\mathrm{ESCS}}_{\cdot g})\)と集団レベルの説明変数\(\overline{\mathrm{ESCS}}_{\cdot g}\),そしてこれらの交互作用項に対して,固定効果の回帰係数が1つずつ推定されることになります。
それでは,このモデルもglmmTMB()関数で実行してみましょう。 変量効果の部分はすでに(escs_cwc|school_id)で指定しているので,説明変数をformulaの右辺に追加するだけで実行できます。 交互作用項を追加する場合には,+の代わりに*を使って繋げましょう。 *を使うと,説明変数の主効果と交互作用項の両方が自動的に追加されます。
Family: gaussian ( identity )
Formula:
read_score ~ escs_cwc * sch_escs_mean + (escs_cwc | school_id)
Data: dat
AIC BIC logLik -2*log(L) df.resid
66498.0 66551.3 -33241.0 66482.0 5758
Random effects:
Conditional model:
Groups Name Variance Std.Dev. Corr
school_id (Intercept) 1463 38.24
escs_cwc 107 10.34 -0.17
Residual 5513 74.25
Number of obs: 5766, groups: school_id, 183
Dispersion estimate for gaussian family (sigma^2): 5.51e+03
Conditional model:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 518.0581 3.1314 165.44 < 2e-16 ***
escs_cwc 7.4769 1.8728 3.99 6.54e-05 ***
sch_escs_mean 126.5833 8.1517 15.53 < 2e-16 ***
escs_cwc:sch_escs_mean 0.4573 4.8602 0.09 0.925
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1得られた推定値を(9.43)式に代入すると, \[ \begin{alignedat}{2} \text{(レベル1)} \quad & y_{pg} & & = \beta_{0g} +\beta_{\mathrm{ESCS},g}(\mathrm{ESCS}_{pg}-\overline{\mathrm{ESCS}}_{\cdot g})+ u_{pg} \\ \text{(レベル2)} \quad & \beta_{0g} & & = 518.0581 + 126.5833\overline{\mathrm{ESCS}}_{\cdot g} + u_{0g}\\ \text{(レベル2)} \quad & \beta_{\mathrm{ESCS},g} & & = 7.4769 +0.4573\overline{\mathrm{ESCS}}_{\cdot g} + u_{\mathrm{ESCS},g} \end{alignedat} \tag{9.45}\] となります(変量効果の部分は省略)。 一番下の式から,このモデルにおいては,ESCSの集団平均(\(\overline{\mathrm{ESCS}}_{\cdot g}\))が大きい集団ほど,個人レベルのESCSの正の効果が大きくなることが示されました。 ただし,係数が小さく,また\(p\)値も大きいことから,基本的には「ESCSの集団平均による違いはほとんどない」と言っても良さそうです。
単純傾斜分析
今回の分析では見られなかったのですが,(クロスレベル)交互作用がある場合には,ある説明変数(\(\mathrm{ESCS}_{pg} - \overline{\mathrm{ESCS}}_{\cdot g}\))回帰係数の傾きが,別の説明変数(\(\overline{\mathrm{ESCS}}_{\cdot g}\))の値によって変わることになります。 これを視覚的に表すために用いられることがあるのが,単純傾斜分析(simple slope analysis)です。 Rで実行する方法はいくつかあると思いますが,ここではmodelbasedパッケージを使って,単純傾斜分析を行う方法を紹介します15。
単純傾斜分析では,傾きを検討したい説明変数(ここではescs_mean)に対する交互作用項(ここではsch_escs_mean)が平均\(\pm1\)標準偏差などの特定の値を取るときに,回帰係数の値について検定を行います。
Estimated Marginal Effects
sch_escs_mean | Slope | SE | 95% CI | z | p
-------------------------------------------------------------
-1.11 | 6.97 | 5.04 | [-2.92, 16.86] | 1.38 | 0.167
-0.89 | 7.07 | 4.05 | [-0.86, 15.00] | 1.75 | 0.081
-0.68 | 7.17 | 3.21 | [ 0.88, 13.45] | 2.23 | 0.025
-0.46 | 7.27 | 2.38 | [ 2.61, 11.92] | 3.06 | 0.002
-0.25 | 7.36 | 1.83 | [ 3.79, 10.94] | 4.03 | < .001
-0.03 | 7.46 | 1.80 | [ 3.93, 10.99] | 4.14 | < .001
0.18 | 7.56 | 2.39 | [ 2.87, 12.25] | 3.16 | 0.002
0.40 | 7.66 | 3.13 | [ 1.52, 13.80] | 2.45 | 0.014
0.61 | 7.76 | 3.96 | [-0.01, 15.53] | 1.96 | 0.050
0.83 | 7.86 | 5.07 | [-2.08, 17.79] | 1.55 | 0.121
Marginal effects estimated for escs_cwc
Type of slope was dY/dXestimate_slopes()関数では,trendに与えた変数(escs_cwc)を説明変数とした回帰直線の傾きが,byに与えた変数(sch_escs_mean)の値によってどう変化するかを表示してくれます。 デフォルトでは,byに与えた変数について,データ内に存在する範囲を10等分した値の場合の傾きをそれぞれ表示しています。 また,以下のように引数byの書き方を変えると,特定の値における結果を表示することも可能です。
Estimated Marginal Effects
sch_escs_mean | Slope | SE | 95% CI | z | p
------------------------------------------------------------
-0.50 | 7.25 | 2.46 | [2.43, 12.07] | 2.95 | 0.003
0.00 | 7.48 | 1.87 | [3.80, 11.15] | 3.99 | < .001
0.50 | 7.71 | 3.54 | [0.77, 14.64] | 2.18 | 0.029
Marginal effects estimated for escs_cwc
Type of slope was dY/dXEstimated Marginal Effects
sch_escs_mean | Slope | SE | 95% CI | z | p
------------------------------------------------------------
-0.46 | 7.27 | 2.37 | [2.61, 11.92] | 3.06 | 0.002
-0.10 | 7.43 | 1.76 | [3.98, 10.88] | 4.22 | < .001
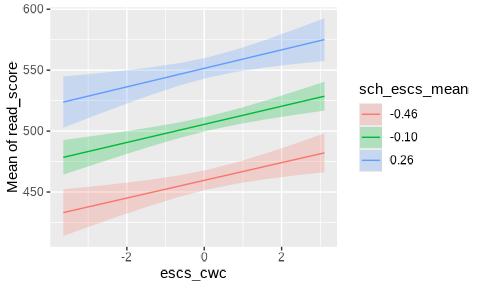
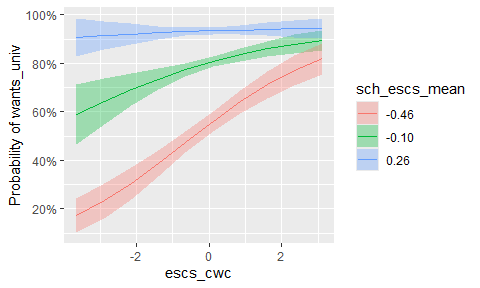
0.26 | 7.60 | 2.75 | [2.22, 12.98] | 2.77 | 0.006
Marginal effects estimated for escs_cwc
Type of slope was dY/dX今回の分析においては,そもそも交互作用が有意でないため,\(\pm1\)標準偏差の間では傾きはほぼ同じになっており,検定もすべて有意となっています。
単純傾斜検定においてよく用いられるのが,特定の条件における回帰直線を実際に引いてみる,というものです。 このためには,まず説明変数の値で条件づけた期待値を計算する必要があります。
引数byの中で,最初に指定した変数を\(X\)軸に置き,2つめに指定した変数の値ごとにそれぞれ回帰直線をプロットします。 今回の場合は,傾きのクロスレベル交互作用がほぼ見られなかったため,傾きはほぼ同じで切片だけが異なる直線となりました。
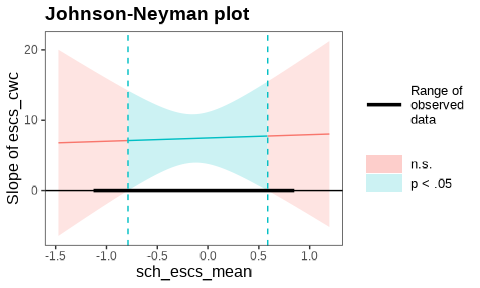
単純傾斜分析の考え方を拡張すると,「sch_escs_meanがある値以下の学校では傾きが有意になり,ある値を超えると有意ではなくなる」などと考えることができます。 これを表すために用いられるのが,Johnson-Neyman区間 (Bauer & Curran, 2005; Johnson & Fay, 1950) と呼ばれるものです。
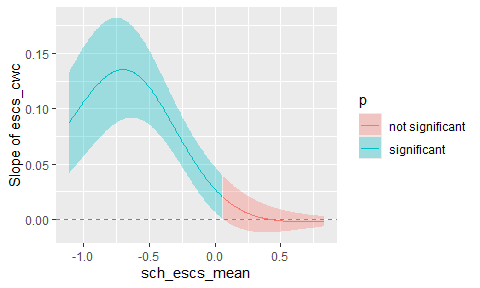
出力の各行は,byに与えた交互作用の説明変数がStartからEndの間の値であるときに有意(\(p<0.05\))であるかをそれぞれあらわしています。 したがって1行目から順に見ていくと,sch_escs_meanが\([-1.11, -0.82]\)の範囲ではescs_cwcの傾きが有意ではなく,\([-0.80, 0.56]\)の範囲では有意,そして\(0.58\)以上では再び有意ではなくなる,ということです16。 なおこの結果は,estimate_slopes()関数で計算された結果をそのまま使っているだけなので,区間の精度を上げたい場合には,それだけ引数lengthを増やせばOKです。
Johnson-Neyman区間の精度を上げるために,試しにlengthを増やしてみましょう。
Johnson-Neymann Intervals
Start | End | Direction | Confidence
-------------------------------------------
-1.11 | -0.81 | positive | Not Significant
-0.80 | 0.54 | positive | Significant
0.55 | 0.55 | positive | Not Significant
0.56 | 0.56 | positive | Significant
0.57 | 0.58 | positive | Not Significant
0.59 | 0.59 | positive | Significant
0.60 | 0.83 | positive | Not Significant
Marginal effects estimated for escs_cwc
Type of slope was dY/dXすると,\(0.55\)から\(0.60\)の間でNot SignificantとSignificantを行き来しました。 これは,sch_escs_meanの値が大きくなるにつれて,傾きと標準誤差が同時に大きくなるためと考えられます。 つまり,sch_escs_meanの値が\(0.55\)から\(0.60\)の間では\(p\)値がほぼ0.05に近いために起こっています(そんなに頻繁に起こることではないと思います)。
この場合の解釈は悩ましいところですが,基本的にはこのように曖昧なところは,有意ではないものとして解釈しておいたほうが良い気がします。 これは,迷った場合には保守的な態度を取ったほうが安全であり,またJohnson-Neyman区間を単一の区間として表せるためです。
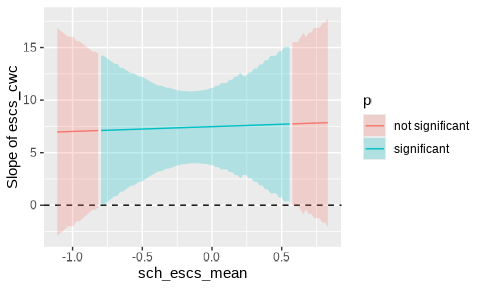
estimate_slopes()関数の出力をplot()にかけると,Johnson-Neyman区間を図示することが可能です。 これは,sch_escs_meanの値が具体的にどの区間にあるときにescs_cwcの傾きが有意になるかを視覚的にわかりやすく示すツールです。
このように,単純傾斜分析やJohnson-Neymanプロットを用いることで,クロスレベルの交互作用がある場合に,どのような状況で傾きが有意になるかを確認することができます。 研究仮説の精緻な検証や,結果の解釈に役立つかもしれません。
lme4とinteractionの組み合わせの場合
ここまでの分析は,lme4::lmer()の出力に対しても同じように実行可能です。 また,interactionパッケージでも以下のように実行可能です。 modelbasedパッケージはまだバージョンが1になっていないので,今後使えなくなる可能性を考慮して,interactionパッケージでの実行方法をいかに示します。 ただし,以下に示す方法の一部はglmmTMB()関数の出力に対しては適用できない点にご注意ください。
単純傾斜分析として,sch_escs_meanの値が特定の状況でのescs_cwcの回帰係数(傾き)を表示するためには,interaction_plot()関数を使用します。
interactions)
interact_plot()関数では,predに与えた変数(escs_cwc)を説明変数とした回帰直線の傾きが,modxに与えた変数(sch_escs_mean)の値によってどう変化するかを表示してくれます。 デフォルトでは,modxの値が平均値\(\pm1\)標準偏差の場合の傾きを表示します。 また,interval = TRUEを指定すると,回帰直線の95%信頼区間も表示されます。
さらに,特定の状況における傾きについて,具体的に検定を行うことも可能です。
JOHNSON-NEYMAN INTERVAL
When sch_escs_mean is INSIDE the interval [-0.79, 0.59], the slope of
escs_cwc is p < .05.
Note: The range of observed values of sch_escs_mean is [-1.11, 0.83]
SIMPLE SLOPES ANALYSIS
Slope of escs_cwc when sch_escs_mean = -0.46161665 (- 1 SD):
Est. S.E. t val. p
------ ------ -------- ------
7.26 2.36 3.08 0.00
Slope of escs_cwc when sch_escs_mean = -0.09878821 (Mean):
Est. S.E. t val. p
------ ------ -------- ------
7.43 1.77 4.21 0.00
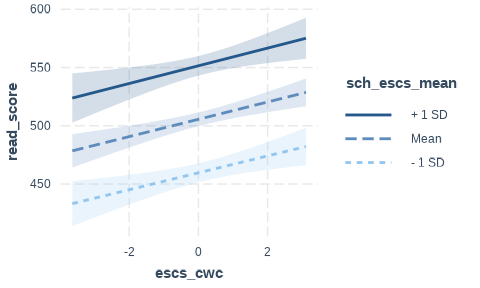
Slope of escs_cwc when sch_escs_mean = 0.26404024 (+ 1 SD):
Est. S.E. t val. p
------ ------ -------- ------
7.60 2.64 2.88 0.00sim_slopes()関数は,interact_plot()関数と同じ引数をとり,特定の状況において「傾きが0である」という帰無仮説に対する検定の結果を表示します。 したがって,上の結果からは,sch_escs_meanが平均値あるいは\(\pm1\)標準偏差くらいの範囲にある学校においては,いずれも個人レベルのESCSの効果が有意であることがわかります。
Johnson-Neyman区間のプロットを出すためには,johnson_neyman()関数を使用します。
プロットにおいて,青い線が表示されている範囲が,「sch_escs_meanがその値のときにはescs_cwcの傾きが有意になる」範囲です。 具体的な値は,同時に出力された中に示されており,今回のケースでは[-0.79, 0.59]の範囲であれば有意であると分かります。
さらなる集団レベル変数の追加
もちろんランダム傾きモデルでも,集団レベルのみの説明変数を追加することは可能です。 ランダム切片モデルのときと同様に,ST比を切片および傾きの説明変数に追加した以下のモデルを考えてみましょう。
\[ \begin{alignedat}{2} \text{(レベル1)} \quad & y_{pg} & & = \beta_{0g} +\beta_{\mathrm{ESCS},g}(\mathrm{ESCS}_{pg}-\overline{\mathrm{ESCS}}_{\cdot g})+ u_{pg} \\ \text{(レベル2)} \quad & \beta_{0g} & & = \mu + \beta_{0,\overline{\mathrm{ESCS}}}\overline{\mathrm{ESCS}}_{\cdot g} + \beta_{0,\mathrm{ST}}\mathrm{ST}_{\cdot g} + u_{0g}\\ \text{(レベル2)} \quad & \beta_{\mathrm{ESCS},g} & & = \beta_{\mathrm{ESCS}} +\beta_{1,\overline{\mathrm{ESCS}}}\overline{\mathrm{ESCS}}_{\cdot g} + \beta_{1,\mathrm{ST}}\mathrm{ST}_{\cdot g} + u_{\mathrm{ESCS},g} \end{alignedat} \tag{9.46}\]
このモデルにおいて,集団レベルの説明変数であるST比は,統制変数のような位置づけです。 例えば,ESCSが平均的に高い学校(有名私立など?)では,よりきめ細かい教育を目指してST比が小さくなる傾向があるとしたら,ESCSが読解力に与える影響は,部分的にはST比によるものである可能性があります。 統制変数を追加するということは,このST比の効果を統制することで,集団レベルのESCSそのもののより純粋な効果を推定するために必要かもしれないのです。 このあたりは,マルチレベルモデルであるかに関わらず,回帰分析においては同じように考えておくと良いでしょう。
それでは,このモデルもglmmTMB()関数で実行してみましょう。 先ほどと同様に,クロスレベル交互作用項の位置に気をつけると,\(\overline{\mathrm{ESCS}}_{\cdot g}(\mathrm{ESCS}_{pg}-\overline{\mathrm{ESCS}}_{\cdot g})\)に加えて,\(\mathrm{ST}_{\cdot g}(\mathrm{ESCS}_{pg}-\overline{\mathrm{ESCS}}_{\cdot g})\)もあることから,以下のようになります。
Warning in finalizeTMB(TMBStruc, obj, fit, h, data.tmb.old): Model
convergence problem; non-positive-definite Hessian matrix. See
vignette('troubleshooting') Family: gaussian ( identity )
Formula:
read_score ~ escs_cwc * (sch_escs_mean + s_t_ratio) + (escs_cwc |
school_id)
Data: dat
AIC BIC logLik -2*log(L) df.resid
NA NA NA NA 5756
Random effects:
Conditional model:
Groups Name Variance Std.Dev. Corr
school_id (Intercept) 1.416e+03 3.763e+01
escs_cwc 1.329e-09 3.645e-05 -1.00
Residual 5.555e+03 7.453e+01
Number of obs: 5766, groups: school_id, 183
Dispersion estimate for gaussian family (sigma^2): 5.55e+03
Conditional model:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 500.0676 8.5274 58.64 < 2e-16 ***
escs_cwc 12.8474 4.4287 2.90 0.00372 **
sch_escs_mean 122.4814 8.2412 14.86 < 2e-16 ***
s_t_ratio 1.4621 0.6458 2.26 0.02358 *
escs_cwc:sch_escs_mean 1.5242 4.4683 0.34 0.73302
escs_cwc:s_t_ratio -0.4387 0.3352 -1.31 0.19063
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1交互作用の追加は,掛け算の分配法則のように考えていけばOKです。 すなわち,固定効果をescs_cwc * (sch_escs_mean+s_t_ratio)と書けば,これはescs_cwc * sch_escs_mean + escs_cwc * s_t_ratioと同じ意味になります。 一方で,もしもescs_cwc * sch_escs_mean * s_t_ratioと書いてしまうと,sch_escs_meanとs_t_ratioの間およびこれとescs_cwcの3つの組み合わせにもすべて交互作用があるものとして解釈されてしまいます。
出力を見ると,Warningが出ており,escs_cwcの傾きの変量効果の分散\(\sigma_{\mathrm{ESCS},g}^2\)の値がほぼゼロになっています。 ということで,今回のデータではうまく変量効果を推定することができませんでした17。
不適解であることに目を瞑って,得られた係数を(9.46)式に代入すると, \[ \begin{alignedat}{2} \text{(レベル1)} \quad & y_{pg} & & = \beta_{0g} +\beta_{\mathrm{ESCS},g}(\mathrm{ESCS}_{pg}-\overline{\mathrm{ESCS}}_{\cdot g})+ u_{pg} \\ \text{(レベル2)} \quad & \beta_{0g} & & = 500.0676 + 122.4814\overline{\mathrm{ESCS}}_{\cdot g} + 1.4621\mathrm{ST}_{\cdot g} + u_{0g}\\ \text{(レベル2)} \quad & \beta_{\mathrm{ESCS},g} & & = 12.8474 +1.5242\overline{\mathrm{ESCS}}_{\cdot g} -0.4387\mathrm{ST}_{\cdot g} + u_{\mathrm{ESCS},g} \end{alignedat} \tag{9.47}\] となります。
9.3.6 モデル比較
ここまで色々なモデルを実行してきましたが,結局のところどこまでの変量効果を考えるべきか,というのは実用上重要なポイントです。 ランダム切片モデルによって求めたICCでは,まずデータの階層性を考慮する必要があるかを確認しましたが,それ以上のモデルを考える必要があるかどうかは,モデル比較によって判断することができます。
まずは,ここまでに実行してきたモデルのformulaを一覧にしておきましょう。 表 9.2 を見ると,一部のモデルはネストの関係にあることが分かります。 例えば,model0は,model2においてsch_escs_meanの回帰係数を0に固定した(集団レベルの説明変数を削除した)モデル,とみなすことができます。
| model | formulaの右辺 |
|---|---|
| model0 | (1|school_id) |
| model1 | escs + (1|school_id) |
| model2 | sch_escs_mean + (1|school_id) |
| model3 | escs_cwc + sch_escs_mean + (1|school_id) |
| model4 | escs_cwc + sch_escs_mean + s_t_ratio + (1 | school_id) |
| model5 | escs_cwc + (1 + escs_cwc | school_id) |
| model6 | escs_cwc * sch_escs_mean + (1 + escs_cwc | school_id) |
| model7 | escs_cwc * (sch_escs_mean + s_t_ratio) + (1 + escs_cwc | school_id) |
このように,モデルがネストの関係にある場合には,尤度比検定(Likerlihood ratio test [LRT])を用いて,モデルの比較を行うことができます。 尤度比検定自体は チャプター 7 でも少しだけ登場しましたが,これは簡単に言えば増やしたパラメータに見合うだけの尤度の改善が見られるかを評価する方法です18。
ということで,明確にネストの関係にあるmodel0,model2,model3,model6の4つのモデルを比較してみましょう19。 これは非常に簡単に,anova()関数を用いて実行できます20。
Data: dat
Models:
model0: read_score ~ (1 | school_id), zi=~0, disp=~1
model2: read_score ~ sch_escs_mean + (1 | school_id), zi=~0, disp=~1
model3: read_score ~ escs_cwc + sch_escs_mean + (1 | school_id), zi=~0, disp=~1
model6: read_score ~ escs_cwc * sch_escs_mean + (escs_cwc | school_id), zi=~0, disp=~1
Df AIC BIC logLik deviance Chisq Chi Df Pr(>Chisq)
model0 3 66671 66691 -33332 66665
model2 4 66519 66545 -33255 66511 154.0264 1 < 2.2e-16 ***
model3 5 66498 66531 -33244 66488 22.6635 1 1.93e-06 ***
model6 8 66498 66551 -33241 66482 5.9989 3 0.1117
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1このように,anova()関数にネストの関係にあるモデルを順番に指定するだけで,モデル比較ができます。 基本的に,パラメータが増えるほど,(対数)尤度を表すlogLikの値は大きくなります。 そして,anova()関数では,この改善した尤度の大きさと追加したパラメータの数(Dfに等しい)を比較して,その改善が有意かどうかを検定してくれます。 今回のデータでは,model0よりもmodel2が,またmodel2よりもmodel3が,それぞれ有意に尤度を改善している一方で,model6はmodel3と比べて有意な改善が見られなかった,と言えます。 したがって,「傾きの変量効果を追加したこと」あるいは「クロスレベル交互作用を追加したこと」の少なくともいずれか(たぶん後者)は,このデータにおいてはあまり意味がなかったのだと言えそうです。 ただし,この結果はもちろんサンプルサイズが大きいほど有意になりやすいので,注意が必要です。
また,anova()関数では情報量規準(AIC, BIC)も出してくれます。 必要に応じてこれらも参考にすると良いでしょう。 その他にも,説明変数を追加したことによる分散説明率を示すPVEや,「推定された変量効果と相関を持つレベル2説明変数を入れ忘れていないか」を確認するなど,説明変数の選択は多角的に行うことが重要とされています (尾崎 他,2018)。
9.4 一般化線形モデル
ここまで紹介してきた階層線形モデルの考え方は,一般化線形モデル(GLM)に対しても同様に適用可能です21。 そこで,ここからはGLMにおける変量効果の考え方を紹介するため,被説明変数を「進学希望(wants_univ)」としたロジスティック回帰分析をマルチレベルで実行していきます。
9.4.1 ランダム切片GLM
まずは,ランダム切片モデルです。 変量効果を考える前に,まず学校ごとの切片を固定効果とみなした場合のモデル式は以下のようになります。 \[
g(y_{pg}) = \log\frac{y_{pg}}{1-y_{pg}} = \beta_0 + \beta_{02} x_{g=2} + \beta_{03} x_{g=3} + \cdots + \beta_{0G} x_{g=G} + u_{pg}
\tag{9.48}\] このモデルをglm()関数で実行する場合には,以下のように書けば良かったですね。
Call:
glm(formula = wants_univ ~ school_id, family = binomial, data = dat)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 1.757e+01 6.687e+02 0.026 0.979
school_id002 -1.817e+01 6.687e+02 -0.027 0.978
school_id003 -1.698e+01 6.687e+02 -0.025 0.980
school_id004 -1.775e+01 6.687e+02 -0.027 0.979
school_id005 -1.776e+01 6.687e+02 -0.027 0.979
school_id006 -1.068e-07 9.599e+02 0.000 1.000
school_id007 -1.479e+01 6.687e+02 -0.022 0.982
[ reached 'max' / getOption("max.print") -- omitted 176 rows ]
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 6572.3 on 5765 degrees of freedom
Residual deviance: 4782.7 on 5583 degrees of freedom
AIC: 5148.7
Number of Fisher Scoring iterations: 16得られた係数から,各学校におけるwants_univの期待値\(\hat{y}_{pg}\)を求める場合には,\(g(y_{pg})\)を\(y_{pg}\)に戻すように変換したら良いので, \[
\begin{alignedat}{2}
\hat{y}_{pg} &= \frac{\exp\left(g(y_{pg})\right)}{1+\exp\left(g(y_{pg})\right)} \\
&= \frac{\exp\left(\beta_0 + \beta_{02} x_{g=2} + \beta_{03} x_{g=3} + \cdots + \beta_{0G} x_{g=G}\right)}{1+\exp\left(\beta_0 + \beta_{02} x_{g=2} + \beta_{03} x_{g=3} + \cdots + \beta_{0G} x_{g=G}\right)}
\end{alignedat}
\tag{9.49}\] となります。 ここに,先ほど推定された値を代入すると,各学校における平均値はそれぞれ \[
\begin{alignedat}{2}
\hat{y}_{p1} &= \frac{\exp(17.57)}{1+\exp(17.57)}&&\approx 1 \\
\hat{y}_{p2} &= \frac{\exp(17.57-18.17)}{1+\exp(17.57-18.17)} &&\approx 0.354 \\
\hat{y}_{p3} &= \frac{\exp(17.57-16.98)}{1+\exp(17.57-16.98)} &&\approx 0.643 \\
\vdots
\end{alignedat}
\tag{9.50}\] などと求めることができます。
もちろん,このままでは先程と同様に「このデータに含まれる学校の間では進学希望率が異なる」以上のことは言えないので,さっそく変量効果を考えていきましょう。
GLMについて変量効果を考える場合,線形予測子の部分に対して正規分布に従うものがあると考えます。 GLMでは,(9.48)式にあるように,被説明変数のタイプにかかわらず,「被説明変数を何らかの形に変換したもの(\(g(y)\))」が「説明変数と回帰係数の線形和(\(\boldsymbol{X}\boldsymbol{\beta} = \beta_0 + \beta_1x_1 + \beta_2x_2 +\cdots\))」で表されると考えます。 したがって,切片を変量効果としたランダム切片GLMは,以下のように書くことができます。
\[ g(y_{pg}) = \log\frac{y_{pg}}{1-y_{pg}} = \mu + u_{0g} \tag{9.51}\] あるいはレベルごとに分割すると, \[ \begin{alignedat}{2} \text{(レベル1)} \quad & g(y_{pg}) & & = \beta_{0g} \\ \text{(レベル2)} \quad & \beta_{0g} & & = \mu + u_{0g} \end{alignedat} \tag{9.52}\] という形になります。 通常の線形モデルとの違いとして,ロジスティック回帰(やポアソン回帰)では,レベル1の変量効果(\(u_{pg}\))が存在しません。 ロジスティック回帰の場合,\(y_{pg}\)の確率分布(尤度関数)は \[ y_{pg} \sim \mathrm{Bernoulli}(p_{pg}) \quad \text{with } p_{pg} = \frac{\exp\left(g(y_{pg}\right))}{1+\exp\left(g(y_{pg})\right)} \tag{9.53}\] と,ベルヌーイ分布として表されます。 そして,ベルヌーイ分布の分散は,この\(p_{pg}\)の関数\(p_{pg}(1-p_{pg})\)であることから,レベル1の要素として独立に分散を考えることが出来ないのです22。 これに対して正規分布(通常の階層線形モデル)の場合には,期待値と分散は無関係であることから,「期待値に影響する」レベル2変量効果と,「分散に影響する」レベル1変量効果という形で,異なるレベルの変量効果がそれぞれ規定できるのです。
以上より,変量効果に関する仮定は,以下のように設定されます。 \[ \text{(レベル2)} \quad u_{0g} \sim N(0, \sigma^2_{0g}) \tag{9.54}\] レベル1(個人レベル)の変量効果こそないものの,GLMにおいても変量効果を考える場合には,線形予測子の部分に対して正規分布に従うものがあると考えれば良いのです。 ただし,この場合変量効果の分散\(\sigma^2_{0g}\)は,\(y\)の分散を表したものではない点には注意してください。 この解釈はやや複雑なので,後ほど数値例とともに紹介していくことにします。
ということで,Rで上記のモデルを実行してみましょう。 といっても,使用する関数はglmmTMB()のままでOKです。 この関数はGLMにも対応しています。 ただしglm()関数と同じように,被説明変数が従う確率分布と,必要に応じてリンク関数を指定する必要があります。
Family: binomial ( logit )
Formula: wants_univ ~ (1 | school_id)
Data: dat
AIC BIC logLik -2*log(L) df.resid
5374.7 5388.0 -2685.3 5370.7 5764
Random effects:
Conditional model:
Groups Name Variance Std.Dev.
school_id (Intercept) 2.164 1.471
Number of obs: 5766, groups: school_id, 183
Conditional model:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 1.449 0.118 12.28 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1lme4パッケージの場合
lm()関数に対してglm()関数が用意されていたように,lme4パッケージではlmer()関数に対してもglmer()という関数が用意されています。
Generalized linear mixed model fit by maximum likelihood (Laplace
Approximation) [glmerMod]
Family: binomial ( logit )
Formula: wants_univ ~ (1 | school_id)
Data: dat
AIC BIC logLik -2*log(L) df.resid
5374.7 5388.0 -2685.3 5370.7 5764
Scaled residuals:
Min 1Q Median 3Q Max
-4.4188 -0.5060 0.2857 0.4988 2.0516
Random effects:
Groups Name Variance Std.Dev.
school_id (Intercept) 2.161 1.47
Number of obs: 5766, groups: school_id, 183
Fixed effects:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 1.448 0.117 12.37 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1得られた推定値を(9.52)式に代入すると, \[ \begin{alignedat}{2} \text{(レベル1)} \quad & g(y_{pg}) & & = \beta_{0g} \\ \text{(レベル2)} \quad & \beta_{0g} & & = 1.449 + u_{0g},\quad u_{0g} \sim N(0, 1.471^2) \end{alignedat} \tag{9.55}\] となります。 \(\mu=1.449\)ということは,ある意味で最も「平均的な」学校における進学希望率は, \[ \hat{y}_{pg} = \frac{\exp(1.449)}{1+\exp(1.449)} \approx 0.810 \tag{9.56}\] となることを意味します。
ロジスティック回帰やポアソン回帰では,期待値に応じて分散が自動的に決定してしまいます。 しかし,この「分散が期待値の関数で表される」という仮定は,実際のデータではかなり強い制約となることがあります。 先ほど実行したモデルでは,進学希望率が学校ごとに異なることを考慮していた一方で,実際にはそれ以外の要因(個人のやる気など)によってもさらなるばらつきが発生する可能性があります。 もちろん,そのような要因は後ほど行うようにモデルの中に説明変数として加えてしまえば良いのですが,もちろんすべての要因を説明変数として加えることはできません。
そこで,「レベル2の変量効果および説明変数では説明できない個人のばらつき」に起因する過分散(ovedispersion)に対応するために,以下のような方法を取ることがあります。
確率分布を変える
同じデータに適用可能な確率分布の中で,パラメータが多いものを用いることで,分散を期待値の関数から切り離す,というのがもっともよく用いられる方法です。 ベルヌーイ分布(二項分布)に対しては,ベータ二項分布という分布がよく用いられます。 これは残念ながらlme4パッケージでは対応できないのですが,以下のようにglmmTMBパッケージ(やbrmsパッケージ)を用いることで,ベータ二項分布を用いたマルチレベルモデルを実行することができます。
同様に,ポアソン分布に対しては負の二項分布(negative binomial distribution)を用いることができます。
ちなみに負の二項回帰は,lme4パッケージにあるglmer.nb()という関数でも実行可能です。
レベル1の変量効果をあえて追加する
言うまでもなく,レベル1の固定効果を加えてしまうと,それだけでサンプルサイズと同数のパラメータが追加されてしまうので,これは不可能です。 一方で変量効果の場合,モデル上は個人ごとのばらつきの具体的な値ではなく,その分散だけを推定するため,観測レベル変量効果 (Observation-level random effects [OLRE]: Harrison, 2014) を指定することも可能なようです。
この場合,レベル1変量効果が追加されることからモデル式は(9.8)式とほぼ同じ形の \[ \begin{alignedat}{2} \text{(レベル1)} \quad & g(y_{pg}) & & = \beta_{0g} + u_{pg} \\ \text{(レベル2)} \quad & \beta_{0g} & & = \mu + u_{0g} \end{alignedat} \tag{9.57}\] となります。 このとき,\(u_{pg}\)の分散\(\sigma_{pg}^2\)を追加で推定するために,過分散に対応できるようになるようです。
OLREは,glmmTMB()での実装も非常に簡単です。 変量効果に関する記述を(1|school_id) + (1|student_id)とすることで,個人レベルの変量効果も考慮することができます。
Family: binomial ( logit )
Formula: wants_univ ~ (1 | school_id) + (1 | student_id)
Data: dat
AIC BIC logLik -2*log(L) df.resid
5376.7 5396.7 -2685.3 5370.7 5763
Random effects:
Conditional model:
Groups Name Variance Std.Dev.
school_id (Intercept) 2.164e+00 1.4710382
student_id (Intercept) 2.261e-08 0.0001504
Number of obs: 5766, groups: school_id, 183; student_id, 5766
Conditional model:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 1.449 0.118 12.28 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1図 9.19 は,モデルで推定された各学校の\(\beta_{0g}\)の値に基づく進学希望割合と,実際にその学校で観測された進学希望割合の散布図です。 実は今回のデータでは,過分散がほとんど発生していないため,student_idのRandom effectsの分散はほぼゼロになっています。 このような場合には,わざわざレベル1変量効果を追加する必要はないのですが,方法だけ紹介しておきました。
ちなみに,過分散であるかどうかを確認する関数も,performanceパッケージに用意されています。すごいですね。 check_overdispersion()関数では,「過分散度」に当たるdispersion ratioが1であるという帰無仮説に対して検定を行ってくれます。 したがって,この値が1より大きい場合には過分散が発生していると考えられるわけです。
変量効果の解釈
\(u_{0g}\)の分散が\(1.47^2\)と出ましたが,これが実際に「学校ごとの進学希望率のばらつき」としてはどの程度になるのでしょうか。 これを確認する直感的な方法は,以下のように「データ内に存在する学校でのモデル上の予測値」の分布を見たり分散を計算することでしょう。
この方法でも,実際に学校ごとにばらつきがあることは分かりますが,わざわざ変量効果にした意味が無くなってしまいます。 図 9.20 は,あくまでも母集団からランダムサンプリングされた学校におけるばらつきを示すものです。 あまりきれいな分布にはなっていませんが,本来はスケールを変えたら正規分布に従うような分布になっているはずです。
ということで,変量効果を考慮したモデルベースで学校ごとのばらつきを示す方法としては,以下のように「母集団の\(X\)%の学校が含まれる区間」を示す,というやり方が考えられます (e.g., Austin & Merlo, 2017; Devine et al., 2024)。 まず,\(u_{0g} \sim N(0, 1.471^2)\)ということは,正規分布の性質から,\(X\)%の確率で含まれる値の範囲を求めることは容易です。 実際に,\(\beta_{0g}\)が従う正規分布\(N(1.449, 1.471^2)\)における平均値周りの95%の範囲は,Rでは以下のように求めることができます。
qnorm()は,指定した分位点(quantile)における正規分布の値を求める関数です。 したがって,いま算出された\([-1.434, 4.332]\)という区間は,母集団全体の95%の学校の\(\beta_{0g}\)が含まれる範囲を表しています。 あとはこれを\(y\)のスケールに戻してあげると,母集団全体の95%の学校の進学希望率が含まれる範囲を求めることができます。
このように,ランダム切片GLMにおいては,変量効果を考慮することで,母集団全体の学校の進学希望率のばらつきを示すことができるのです。 ただし今回の場合,95%区間はあまりに広すぎるようなので,例えば50%区間などを求めてみても良いのかもしれません23。
別の方法としては,推定された変量効果の正規分布から乱数を生成する,というやり方も考えられます。
rnorm(n)関数は,正規分布からn個の乱数(random number)を生成してくれる関数です。 これを用いて「母集団に含まれる(仮想的な)学校の\(\beta_{0g}\)」を10万個生成し,それを\(y\)のスケールに戻してヒストグラムを描画したものが 図 9.21 です。 こうして見ても,やはり進学希望率が学校ごとにかなりばらついていることがよく分かります。
9.4.2 級内相関係数の確認
ランダム切片GLMにおいても,級内相関係数(ICC)を求めることができます。 ただし,(9.16)式の定義では2つのレベルの変量効果の分散の割合を用いていたため,レベル1の変量効果がないGLMでは,そのままでは求めることができません。 そのため,ロジスティック回帰分析においては,レベル1変量効果の大きさを仮定するために,ポリコリック相関のときのように二値反応の背後に連続量が存在し,その連続量が標準ロジスティック分布(標準正規分布のようなもの)に従うと仮定します(Snijders & Bosker, 2012)。 この仮定のもとでは,母集団全体におけるレベル1変量効果の分散(個人レベルのばらつき)は,標準ロジスティックの分散\(\frac{\pi^2}{3}\)とおいて考えることに一定の正当性が生まれます。
最終的に,ロジスティック回帰分析における級内相関係数は,以下のように定義されます。 \[ \text{ICC} = \frac{\sigma^2_{0g}}{\sigma^2_{0g} + \frac{\pi^2}{3}} \approx \frac{\sigma^2_{0g}}{\sigma^2_{0g} + 3.29} \tag{9.58}\] となります24。
実際に,推定された変量効果の分散を用いてICCを求めてみましょう。
今回のデータに対するICCは,およそ0.397と大きく,( 図 9.21 などからも明らかですが)やはりマルチレベルな分析を行ったほうが良いと言えそうです。
9.4.3 説明変数を追加したランダム切片GLM
これ以降は,通常の階層線形モデルと同じように説明変数を色々と追加していくだけです。 まずは,ESCS(社会経済的地位)を説明変数として追加してみましょう。 個人レベルおよび集団レベルの効果をそれぞれ説明変数として投入した場合,モデルは以下のようになります。 \[ \begin{alignedat}{2} \text{(レベル1)} \quad & g(y_{pg}) & & = \beta_{0g} + \beta_{\mathrm{ESCS}}(\mathrm{ESCS}_{pg} - \overline{\mathrm{ESCS}}_{\cdot g} ) \\ \text{(レベル2)} \quad & \beta_{0g} & & = \mu + \beta_{\overline{\mathrm{ESCS}}}\overline{\mathrm{ESCS}}_{\cdot g} + u_{0g} \end{alignedat} \tag{9.59}\]
glmmTMB()で実行する場合は,以下のとおりです。
Family: binomial ( logit )
Formula: wants_univ ~ escs_cwc + sch_escs_mean + (1 | school_id)
Data: dat
AIC BIC logLik -2*log(L) df.resid
5122.7 5149.3 -2557.3 5114.7 5762
Random effects:
Conditional model:
Groups Name Variance Std.Dev.
school_id (Intercept) 0.5417 0.736
Number of obs: 5766, groups: school_id, 183
Conditional model:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 1.88638 0.07958 23.703 < 2e-16 ***
escs_cwc 0.38946 0.05521 7.054 1.74e-12 ***
sch_escs_mean 3.58849 0.20254 17.717 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1得られた推定値を(9.59)式に代入すると, \[
\begin{alignedat}{2}
\text{(レベル1)} \quad & g(y_{pg}) & & = \beta_{0g} + 0.38946(\mathrm{ESCS}_{pg} - \overline{\mathrm{ESCS}}_{\cdot g} ) \\
\text{(レベル2)} \quad & \beta_{0g} & & = 1.88638 + 3.58849\overline{\mathrm{ESCS}}_{\cdot g} + u_{0g}, \quad u_{0g} \sim N(0, 0.736^2)
\end{alignedat}
\tag{9.60}\] となります。 推定値を見ると,escs_cwc(個人レベルのESCS)とsch_escs_mean(学校ごとの平均ESCS)の両方の係数(固定効果)が有意であることが分かります。 したがって,ESCSが高い学校の生徒ほど,また同じ学校内でも相対的にESCSが高い生徒ほど進学希望率が高くなる,と言えそうです。
次に,ランダム切片GLMを可視化してみましょう。 図 9.22 は,coef()関数を用いて取得した学校ごとの切片をもとに回帰の線を引いたものです。 赤い線が各学校の回帰線を,青い点線が全体の平均的な回帰線を表しています。
ランダム切片モデルでは,傾きはすべての学校で共通(0.38946)です。 したがって,図ではややわかりにくいですが,赤い実線や青い点線はいずれも,左右に平行移動させたら完全に重なる線です。
9.4.4 ランダム傾きGLM
続いては,ランダム傾きモデルもロジスティック回帰で実行してみましょう。 ランダム傾きモデルでは,レベル2の変量効果が切片だけでなく傾きにも影響を与えます。 まず,レベル2説明変数のないランダム傾きGLMのモデル式は以下のようになります。 \[ \begin{alignedat}{2} \text{(レベル1)} \quad & g(y_{pg}) & & = \beta_{0g} +\beta_{\mathrm{ESCS},g}(\mathrm{ESCS}_{pg}-\overline{\mathrm{ESCS}}_{\cdot g}) \\ \text{(レベル2)} \quad & \beta_{0g} & & = \mu + u_{0g}\\ \text{(レベル2)} \quad & \beta_{\mathrm{ESCS},g} & & = \mu_{\mathrm{ESCS}} + u_{\mathrm{ESCS},g} \end{alignedat} \tag{9.61}\] また,変量効果は以下のようになります。 \[ \begin{alignedat}{2} \text{(レベル2)} &\left[\begin{array}{c} u_{0g} \\ u_{\mathrm{ESCS},g} \end{array}\right] &&\sim MVN\left( \left[\begin{array}{c} 0 \\ 0 \end{array}\right], \left[\begin{array}{cc} \sigma_{0g}^2 & \sigma_{(0g)(\mathrm{ESCS},g)} \\ \sigma_{(0g)(\mathrm{ESCS},g)} & \sigma_{\mathrm{ESCS},g}^2 \end{array}\right]\right) \end{alignedat} \tag{9.62}\] レベル1の回帰式が\(y_{pg}\)そのものではなく\(g(y_{pg})\)であること,またレベル1の変量効果がないことを除けば,通常の階層線形モデルと同じということです。 GLMであっても,やはりレベル2の変量効果(切片・傾き)の間には相関関係を許容することができます。
上記のモデルをRで実行する際も,glmmTMB()を使えば簡単です。
Family: binomial ( logit )
Formula: wants_univ ~ escs_cwc + (escs_cwc | school_id)
Data: dat
AIC BIC logLik -2*log(L) df.resid
5327.4 5360.7 -2658.7 5317.4 5761
Random effects:
Conditional model:
Groups Name Variance Std.Dev. Corr
school_id (Intercept) 2.21612 1.4887
escs_cwc 0.07018 0.2649 -0.28
Number of obs: 5766, groups: school_id, 183
Conditional model:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 1.46466 0.11965 12.241 < 2e-16 ***
escs_cwc 0.35556 0.07242 4.909 9.13e-07 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1得られた推定値を(9.61)式に代入すると, \[ \begin{alignedat}{2} \text{(レベル1)} \quad & g(y_{pg}) & & = \beta_{0g} +\beta_{\mathrm{ESCS},g}(\mathrm{ESCS}_{pg}-\overline{\mathrm{ESCS}}_{\cdot g}) \\ \text{(レベル2)} \quad & \beta_{0g} & & = 1.46466 + u_{0g}\\ \text{(レベル2)} \quad & \beta_{\mathrm{ESCS},g} & & = 0.35556 + u_{\mathrm{ESCS},g} \end{alignedat} \tag{9.63}\] また変量効果は \[ \begin{alignedat}{2} \text{(レベル2)} &\left[\begin{array}{c} u_{0g} \\ u_{\mathrm{ESCS},g} \end{array}\right] &&\sim MVN\left( \left[\begin{array}{c} 0 \\ 0 \end{array}\right], \left[\begin{array}{cc} 1.4887^2 & -0.1104 \\ -0.1104 & 0.2649^2 \end{array}\right]\right) \end{alignedat} \tag{9.64}\] となります。
図 9.23 は,ランダム傾きGLMの回帰線を可視化したものです。 赤い線が各学校の回帰線を,青い点線が全体の平均的な回帰線を表しています。 この図を見ると,学校内での相対的なESCS(escs_cwc)が高い生徒は,所属している高校によらず進学希望率が高い傾向にある一方で,相対的なESCSが低い生徒の進学希望率は高校によってかなりばらつきがあることが分かります。
また,切片と傾きの変量効果の間に負の相関があったことも図で改めて確認しておきましょう。
切片(学校単位の進学希望率)が高い高校ほどescs_cwcの回帰係数が小さい(傾きが緩やかである)どころか負になっていくことが分かります。 このメカニズムとしては,例えば
- 進学希望率の高い進学校などでは,ESCSの高い生徒も低い生徒も進学希望率が高くなるため,傾きが緩やかになる
- 逆に,進学希望率の低い高校では,相対的にESCSの高い生徒でないと進学希望が出せないために,傾きが急になる
といったことが考えられるかもしれません。
lmer::glmer()の実行時に,下記のようなメッセージや警告が出てきた場合は要注意です。
Warning: Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl =
control$checkConv, : Model failed to converge with max|grad| = 0.00483982
(tol = 0.002, component 1)このようなときにsummary(model)の出力をよく見てみると,例えば2つのRandom effectsの相関係数(Corr)の絶対値が1に近い値になっているなど,常識的に考えておかしな推定値が出ていることがあります。 これは,ロジスティック回帰の推定がうまくいっていないことを示しています。
ロジスティック回帰において推定がうまくいかない代表的なケースとして, 図 9.25 の左のように,すべてのケースの被説明変数の値が同じになっている場合や,右のように,説明変数の値が完全に分離している場合が挙げられます。 というのも,ロジスティック回帰の目的は,( 図 9.22 に示されているように),「説明変数の値が大きくなるほど\(y=1\)となる確率がどれだけ変化するか」を推定することです。 しかし,被説明変数の値が全員同じ場合,説明変数の値が変化しても\(y\)の値は変化しないため,S字の曲線が上か下に貼り付いてしまい,係数の推定が発散してしまいます。 同様に,説明変数の値が完全に分離している場合には,ロジスティック曲線の傾きが無限大に発散してしまい,やはりうまくいかないのです。 マルチレベルの場合,このような学校が一つでもあると,このデータも含めて変量効果\(u_{0g},u_{\mathrm{ESCS},g}\)の分散を推定することになるため,計算がおかしくなってしまいます。
データ内に被説明変数の値が全員同じ集団がある場合は,まずそもそもランダム傾きモデルを適用するべきかを考えましょう。 特にそのような集団の割合が大きい場合には,いわば「傾きがゼロ」の集団が無視できないほど多いわけなので,その傾きの大きさの違いを議論することは本質的ではない可能性があります25。
そして,もしたまたまサンプルサイズの小さい集団でたまたまそのようなことが起こっていただけなど,外れ値的に無視しても良さそうと判断できるならば,対策を講じていくことになります。 最もシンプルな対策は,そのような学校を一時的に除外してしまうことです26。 もちろん,そのような学校を除外してしまうことは,固定効果の推定にも影響を与えるため,慎重に行う必要があります。 例えば,全員が\(y_{pg}=0\)の学校を除外してしまうことは,大学進学を希望しない生徒のデータを選択的にゴッソリ除外してしまうことになります。 もしも進学希望とESCSに相関があるならば,これは同時にESCSの低い生徒のデータも除外してしまうことになります。 その結果,使用するデータは「ESCSが比較的高い生徒・学校」のデータのみになってしまう,といった可能性があるわけです。
9.4.5 説明変数を含むランダム傾きGLM
先程の分析では,進学希望率が高い学校ほど,個人レベルのESCSと進学希望率の関係が弱くなる可能性が示されました。 ということで,最後にレベル2説明変数を追加したランダム傾きモデルで,sch_escs_meanが傾きの説明変数として機能するかを確認してみましょう。
\[ \begin{alignedat}{2} \text{(レベル1)} \quad & g(y_{pg}) & & = \beta_{0g} +\beta_{\mathrm{ESCS},g}(\mathrm{ESCS}_{pg}-\overline{\mathrm{ESCS}}_{\cdot g}) \\ \text{(レベル2)} \quad & \beta_{0g} & & = \mu + \beta_{0,\overline{\mathrm{ESCS}}}\overline{\mathrm{ESCS}}_{\cdot g} + u_{0g}\\ \text{(レベル2)} \quad & \beta_{\mathrm{ESCS},g} & & = \beta_{\mathrm{ESCS}} +\beta_{1,\overline{\mathrm{ESCS}}}\overline{\mathrm{ESCS}}_{\cdot g} + u_{\mathrm{ESCS},g} \end{alignedat} \tag{9.65}\]
このモデルをglmmTMB()で実行する場合も,クロスレベル交互作用に気をつけてformulaを正しく指定してください。
Family: binomial ( logit )
Formula:
wants_univ ~ escs_cwc * sch_escs_mean + (escs_cwc | school_id)
Data: dat
AIC BIC logLik -2*log(L) df.resid
5117.2 5163.8 -2551.6 5103.2 5759
Random effects:
Conditional model:
Groups Name Variance Std.Dev. Corr
school_id (Intercept) 0.54961 0.7414
escs_cwc 0.05358 0.2315 0.50
Number of obs: 5766, groups: school_id, 183
Conditional model:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 1.88564 0.08027 23.493 < 2e-16 ***
escs_cwc 0.26730 0.08712 3.068 0.00215 **
sch_escs_mean 3.57660 0.20388 17.543 < 2e-16 ***
escs_cwc:sch_escs_mean -0.50243 0.20912 -2.403 0.01628 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1得られた推定値を(9.65)式に代入すると, \[ \begin{alignedat}{2} \text{(レベル1)} \quad & g(y_{pg}) & & = \beta_{0g} +\beta_{\mathrm{ESCS},g}(\mathrm{ESCS}_{pg}-\overline{\mathrm{ESCS}}_{\cdot g}) \\ \text{(レベル2)} \quad & \beta_{0g} & & = 1.88564 + 3.57660\overline{\mathrm{ESCS}}_{\cdot g} + u_{0g}\\ \text{(レベル2)} \quad & \beta_{\mathrm{ESCS},g} & & = 0.26730 -0.50243\overline{\mathrm{ESCS}}_{\cdot g} + u_{\mathrm{ESCS},g} \end{alignedat} \tag{9.66}\] となります。
単純傾斜分析
クロスレベル交互作用がある場合,単純傾斜分析を行うことで,escs_cwc(個人レベルのESCS)とsch_escs_mean(学校ごとの平均ESCS)の組み合わせごとに,進学希望率の変化を確認することができます。
この図からは,ESCSが高い学校(青)では,個人の相対的なESCSに関わらず進学希望率が高いこと,反対にESCSが低い学校(赤)では,進学希望率が個人の相対的なESCSに強く影響を受けていることがはっきりと分かります。
ということで,変化率の検定も行ってみると,sch_escs_meanが0.06以下の学校では,個人レベルのESCS(escs_cwc)が進学希望率に有意な影響を与えていることが分かりました。
Estimated Marginal Effects
sch_escs_mean | Slope | SE | 95% CI | z | p
-------------------------------------------------------------------
-0.46 | 0.11 | 0.02 | [ 0.08, 0.14] | 7.08 | < .001
-0.10 | 0.04 | 0.01 | [ 0.02, 0.06] | 3.86 | < .001
0.26 | 4.72e-03 | 7.94e-03 | [-0.01, 0.02] | 0.60 | 0.552
Marginal effects estimated for escs_cwc
Type of slope was dY/dXestimate_slopes()関数が計算しているもの
(9.66)式に基づいて,普通に特定の状況における傾きを計算してみると,少し変なことに気づきます。 例えば上にあるように,sch_escs_meanが-0.46(平均\(-1SD\))のときの傾きは, \[
0.26730 - 0.50243 \times (-0.46) \approx 0.4984
\] となるはずですが,estimate_slopes()の出力を見ると0.11となっています。
実はmodelbasedパッケージのestimate_slopes()関数は,デフォルトでは特定の状況における傾きそのものではなく,限界効果 (marginal effect,より具体的には平均限界効果[AME])というものを出力しています。 限界効果は,特に非線形の回帰分析モデルにおいて,係数の解釈をより直感的にするために用いられる指標のようです。
今回のデータでの結果をもとに,なぜ(9.66)式に基づいて普通に傾きを計算してしまうと問題なのかを考えてみましょう。 今回のモデルでは,傾きと切片の変量効果の両方に,同じ説明変数\(\overline{\mathrm{ESCS}}_{\cdot g}\)が含まれていました。 したがって,例えば\(\overline{\mathrm{ESCS}}_{\cdot g}=-2\)のときの回帰曲線の線形予測子の期待値は, \[
\begin{aligned}
g(y_{pg}) &= (1.88564 + 3.57660\times-2) +(0.26730 -0.50243\times-2)(\mathrm{ESCS}_{pg}-\overline{\mathrm{ESCS}}_{\cdot g}) \\
&= -5.26756 + 1.27216(\mathrm{ESCS}_{pg}-\overline{\mathrm{ESCS}}_{\cdot g})
\end{aligned}
\] となります。 この時点では,傾きは\(1.27216\)となかなか大きいのですが,実際に上の式に基づいて回帰曲線を引いてみると, 図 9.28 のように,大半の人のescs_cwcの値の範囲では,局所的な傾きが非常に小さくなっていることが分かります。
このように,非線形な回帰分析においては,局所的な傾きが部分ごとに異なっているのです。 こうした事情を考慮せずに単純に計算した単一の係数によって評価してしまうと,(特に単純傾斜分析では)例えば「ESCSの平均が極端に高い学校では傾きが有意な負の値になる,これは相対的なESCSが高い生徒(トップオブトップ)はむしろ大学進学を希望しなくなることを意味する」といった,変な結果が出てしまいます。
限界効果は,こういった問題をクリアするために,実質的な効果(説明変数が1増えると,予測確率は何パーセント増加するか)を表すために用いられます。 具体的には,傾きが\(\beta\)であるときに,予測確率\(p\)を用いて\(p(1-p)\beta\)として計算される値です。 \(p(1-p)\)は,\(p=0.5\)で最大値を取ります。 そして,ロジスティック曲線も,\(p=0.5\)で傾きが最大になります。 このようにして,局所的な傾きを反映させることで,より実際に即した「効果」の評価を行っているのです。
ちなみに,(9.66)式に基づく傾き(単純傾斜)を計算してほしい場合には,引数を設定する必要があります。
変量効果の相関
なお,model4_glmでは,切片と傾きの変量効果の間に,model3_glmとは反対に正の相関が見られています。 これは変量効果が,通常の回帰分析における誤差項と同じように「(そのレベルの)説明変数によって説明できなかった残りの変動」に相当するためです。 sch_escs_meanという説明変数は,本来(model4_glm)の推定結果が示すように「切片とは正の相関」「傾きとは負の相関」が見られるものでした。 そんな説明変数がmodel3_glmには含まれていなかったために,「説明変数によって説明できなかった残りの変動」に相当する変量効果の間には負の相関が見られたのです。 model4_glmの変量効果には正の相関が見られたということは,sch_escs_meanの影響を取り除いたあとでなお,傾きと切片に対して同じ方向に働くまだ見ぬ説明変数がある可能性を示唆しているのかもしれません27。
9.5 マルチレベルSEM
チャプター 7 で説明したように,回帰分析はSEMの下位モデルとして位置づけることができました。 そこで,階層線形モデルを拡張して,マルチレベルなSEMを考えていきましょう。
9.5.1 マルチレベル相関係数
SEMは,変数間の共分散行列について,「モデル上の共分散行列\(\symbf{\Sigma}\)」と「実際に観測された共分散行列\(\symbf{S}\)」のズレが最小になるようにパラメータを推定する手法でした。 ということで,まずはデータに階層性がある場合の相関係数(共分散)について考えてみましょう。
まずは,データの階層性を無視して,「生徒のESCSの高さと読解力(read_score)の間の相関」を確認してみます。
この値は,生徒のESCSが高いほど読解力も高い傾向があることを示しています。 ただし,前半で見てきたように,この結果は
- ESCSが高い生徒ほど読解力が高い(個人レベル)
- ESCSが高い学校に所属している生徒ほど読解力が高い(集団レベル)
の両方の効果が混ざっている,と考えられます。 ということで前半では,ある変数の個人ごとの値の違い(変動)を, 2つのレベルに分解する考え方( 図 9.7 )に基づいて階層線形モデルを実施していました。
図 9.30 は,図 9.7 と同じ考え方で2変数の(共)変動をイメージしたものです。 共分散を計算する際には,2変数それぞれについて平均値からの偏差を求めて,その平均値を取っていました。 そのため,集団レベルの共分散は「その集団の平均の,全体平均からの偏差(緑の矢印)」,また個人レベルの共分散は「集団平均からの偏差(オレンジの矢印)」に分解することができそうです。 実際に, セクション 9.1.3 の「生態学的誤謬」の例で見たように,階層性を考慮せずに求めた2変数の相関は,個人レベルの相関と集団レベルの相関の効果が組み合わさった形になっていました( 図 9.8 )。
…ということで,階層線形モデルではこのように,単純に変動をレベルごとに分割していたのですが,よく考えると,この分割には少し注意点があります。 それは,集団平均には,厳密には個人レベルの要因の影響が含まれているということです。 ある学校のESCSの平均値が高いとき,それは「ESCSが高い生徒が集まった結果」として観測されたものであるとも考えられるでしょう。
マルチレベルSEMでは,相関係数をレベル別に分解するとき,具体的には集団レベルの相関係数を算出する際に,個人レベルの影響を完全に取り除いた純粋な相関係数 (Kenny & La Voie, 1985; 日本語での解説は 清水,2014 を参照)を使用します。
マルチレベル相関係数を求める
ということで,ここまでの内容を実際に確認しつつ,マルチレベルSEMをlavaanで実行するための準備をしていきましょう。 まずは,1変数の分散が個人レベルと集団レベルに分解できることを確認するため,ランダム切片モデル(変量効果の分散分析)を行ってみます。
lavaanには,level:というキーワードが設定されており,これによって階層ごとにモデルを指定することができます。 したがって,上のmodelの書き方によって,
level: 1(個人レベル)におけるread_scoreの分散を推定するlevel: 2(集団レベル)におけるread_scoreの分散を推定する
という2つの計算を指定しているわけです。 あとは,いつもと同じようにsem()関数を用いてパラメータ推定を行いましょう。 引数clusterに,レベル2の集団を表す列の名前を与えてあげることで,マルチレベルの推定を行うことができます。
lavaan 0.6-20 ended normally after 11 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 3
Number of observations 5766
Number of clusters [school_id] 183
Model Test User Model:
Test statistic 0.000
Degrees of freedom 0
Parameter Estimates:
Standard errors Standard
Information Observed
Observed information based on Hessian
Level 1 [within]:
Variances:
Estimate Std.Err z-value P(>|z|)
read_score 5579.473 105.605 52.833 0.000
Level 2 [school_id]:
Intercepts:
Estimate Std.Err z-value P(>|z|)
read_score 503.699 4.562 110.401 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
read_score 3624.389 398.532 9.094 0.000summaryを見ると,Level 1 [within]:とLevel 2 [school_id]:という2つの出力が得られています。 これが,それぞれ個人レベルと集団レベルの推定値を表しているのです。
ということで,read_scoreの分散は,個人レベルが5579.473,また集団レベルが3624.389となりました。 もちろんこれは,glmmTMB()で得られた結果とも完全に一致しています。
Family: gaussian ( identity )
Formula: read_score ~ (1 | school_id)
Data: dat
AIC BIC logLik -2*log(L) df.resid
66670.7 66690.7 -33332.3 66664.7 5763
Random effects:
Conditional model:
Groups Name Variance Std.Dev.
school_id (Intercept) 3624 60.2
Residual 5579 74.7
Number of obs: 5766, groups: school_id, 183
Dispersion estimate for gaussian family (sigma^2): 5.58e+03
Conditional model:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 503.699 4.562 110.4 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Random effects:のところに示されている変量効果の分散と対応させてみると,個人レベル分散を表すResidualが5579,また集団レベル分散を表すschool_id (Intercept)が3624ということで,lavaanの推定結果とたしかに一致しています。
続いては,2変数の共分散(相関)を分解してみましょう。 基本的な考え方は同じで,個人レベルと集団レベルのそれぞれについてモデル式を書くだけです。 ここでは,read_scoreとescsの共分散について推定してみます。
Warning: lavaan->lav_data_full():
some observed variances are (at least) a factor 1000 times larger
than others; use varTable(fit) to investigatelavaan 0.6-20 ended normally after 52 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 8
Number of observations 5766
Number of clusters [school_id] 183
Model Test User Model:
Test statistic 0.000
Degrees of freedom 0
Parameter Estimates:
Standard errors Standard
Information Observed
Observed information based on Hessian
Level 1 [within]:
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
read_score ~~
escs 3.038 0.640 4.750 0.000 3.038 0.064
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
read_score 5579.112 105.594 52.836 0.000 5579.112 1.000
escs 0.408 0.008 52.828 0.000 0.408 1.000
Level 2 [school_id]:
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
read_score ~~
escs 16.987 2.102 8.080 0.000 16.987 0.810
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
read_score 503.576 4.570 110.200 0.000 503.576 8.350
escs -0.113 0.027 -4.163 0.000 -0.113 -0.324
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
read_score 3637.088 400.130 9.090 0.000 3637.088 1.000
escs 0.121 0.014 8.581 0.000 0.121 1.000この結果を要約すると,read_scoreとescsの共分散行列はレベルごとに \[
\begin{alignedat}{2}
\mathrm{(レベル1)} & \quad &
\mathrm{Cov}\begin{bmatrix}
\mathrm{read\_score} \\
\mathrm{escs}
\end{bmatrix} = \begin{bmatrix}
5579.112 & 3.038 \\
3.038 & 0.408
\end{bmatrix} \\
\mathrm{(レベル2)} & \quad &
\mathrm{Cov}\begin{bmatrix}
\mathrm{read\_score} \\
\mathrm{escs}
\end{bmatrix} = \begin{bmatrix}
3637.088 & 16.987 \\
16.987 & 0.121
\end{bmatrix}
\end{alignedat}
\tag{9.67}\] と分解できることを表しています。 そしてマルチレベル相関係数は,Covariance:のStd.all列を見ることで,レベル1相関係数が0.064,レベル2相関係数が0.810だと分かります。 すなわち,read_scoreとescsの関係は,どちらかといえば「ESCSの高い学校に所属している生徒ほど,読解力が高い」という効果のほうが強そうだ,ということが,相関係数の観点からも言えるわけです。
ちなみにこの結果は,ランダム切片モデルで個人レベルと集団レベルの両方の説明変数を入れた(read_score ~ escs_cwc + sch_escs_mean + (1|school_id))ときに,集団レベルの回帰係数のほうが傾きが大きかったことと対応している( 図 9.15 )と言えます28。
以上のように,マルチレベルSEMでは,共分散行列を「個人レベル」と「集団レベル」に分解したうえで,2つのSEMを同時に実行していると考えると良いでしょう。
9.5.2 階層線形モデルをlavaanで実行する
マルチレベルSEMでは,基本的に2つのレベルについてSEMをそれぞれ実行しているだけなので,あとは自由にモデルを構築してあげるだけです。 ということで,まずは普通の回帰分析(階層線形モデル)を実行してみましょう。 glmmTMB()で得られた結果と比較するため,個人レベル・集団レベルの両方を説明変数として投入したランダム切片モデル(9.29式)をlavaanで実現してみます。
わざわざ図に表すほどでもないのですが, 図 9.31 にモデル図を用意しました。 なおマルチレベルSEMでは,係数がレベルごとに出力されるだけでなく,後述するようにレベルごとに異なるモデルも設定できるため,モデル図を描く際は,例え同じものになるとしてもレベルごとに描いておくのがおすすめです。
図 9.31 では,2つのレベルに投入されている説明変数が,どちらも同じescsとなっています。 glmmTMB()(やlmer())で階層線形モデルを行う際には,異なるレベルの説明変数は事前に用意(escs_cwcとsch_escs_mean)する必要がありました。 一方lavaanでは,異なるlevel:のモデル式に書くだけで自動的にその説明変数をレベルごとに分離してくれます。 ということで, 図 9.31 のモデルをlavaanで実行してみましょう。
lavaanで階層線形モデル
lavaan 0.6-20 ended normally after 47 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 5
Number of observations 5766
Number of clusters [school_id] 183
Model Test User Model:
Test statistic 0.000
Degrees of freedom 0
Parameter Estimates:
Standard errors Standard
Information Observed
Observed information based on Hessian
Level 1 [within]:
Regressions:
Estimate Std.Err z-value P(>|z|)
read_score ~
escs 7.451 1.562 4.769 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.read_score 5556.473 105.165 52.836 0.000
Level 2 [school_id]:
Regressions:
Estimate Std.Err z-value P(>|z|)
read_score ~
escs 140.609 9.103 15.446 0.000
Intercepts:
Estimate Std.Err z-value P(>|z|)
.read_score 519.422 3.153 164.730 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.read_score 1248.501 173.723 7.187 0.000推定された結果を階層線形モデルのような式で表してみると, \[
\begin{alignedat}{3}
\text{(レベル1)} \quad & y_{pg} & & = \beta_{0g} +7.451\mathrm{ESCS}^{*}_{pg}+ u_{pg}, &\quad& u_{pg} \sim N(0, 74.54^2) \\
\text{(レベル2)} \quad & \beta_{0g} & & = 519.422 +140.609\overline{\mathrm{ESCS}}^{*}_{\cdot g} + u_{0g}, &\quad& u_{0g} \sim N(0, 35.33^2)
\end{alignedat}
\tag{9.68}\] となります。 なお,\(\mathrm{ESCS}^{*}_{pg}\)はescsを集団平均で中心化した値のようなものを表しており,同様に\(\overline{\mathrm{ESCS}}^{*}_{\cdot g}\)も,観測された集団平均値そのものではなく,平均値のようなものを表しています。 これは先ほど説明したように,集団レベルの共分散行列を求める際に,より正確に個人レベルの影響を完全に取り除いた純粋な集団レベルの共分散を計算していることに起因します。
その結果,推定値はglmmTMB()で求めた値と基本的にはあまり変わらないのですが,わずかに差が生じます。
Family: gaussian ( identity )
Formula: read_score ~ escs_cwc + sch_escs_mean + (1 | school_id)
Data: dat
AIC BIC logLik -2*log(L) df.resid
66498.0 66531.3 -33244.0 66488.0 5761
Random effects:
Conditional model:
Groups Name Variance Std.Dev.
school_id (Intercept) 1461 38.23
Residual 5557 74.54
Number of obs: 5766, groups: school_id, 183
Dispersion estimate for gaussian family (sigma^2): 5.56e+03
Conditional model:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 518.060 3.132 165.43 < 2e-16 ***
escs_cwc 7.446 1.563 4.77 1.88e-06 ***
sch_escs_mean 126.569 8.153 15.53 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1glmmTMB()によって得られた推定値を式に入れた(9.30)式と比べると,特にレベル2(集団レベル)の式のところで少しばかりの差が生じていることが分かります。
9.5.3 マルチレベルなCFA
続いては,簡単なCFAをマルチレベルモデルで実行してみましょう。 PISA2018では,授業方法に関する4項目(teach1-4)の質問があります。 これを使用して「授業方針」の因子得点を求めてみます( 図 9.32 )。
マルチレベルCFAで推定される因子得点の解釈は,これまでに見てきた個人レベル・集団レベルそれぞれの解釈の違いと基本的には同じです。 したがって, 図 9.32 の\(f_2\)(レベル2因子得点)は「その学校の先生の授業の構成力」のようなものを表している,とみなせそうです。 一方\(f_1\)(レベル1因子得点)は,「授業の構成力」の評価を学校レベルで相対化した値です。 なんだかよく分かりませんが,例えば「先生は,私たちが学んだことを理解しているかどうか、確認するための質問を出す(teach2)」という質問項目などからは「相対的に自分に目をかけてくれているか」のような得点と言えるかもしれません。 あるいは,生徒側の主観として「先生の授業の工夫を受け取ることができているか」を表したものかもしれません。 ……というように,本来マルチレベルCFAを行う際には,レベルごとの因子の解釈がそれぞれどの様になるかを考えることが重要です。 そして,因子の意味はレベルごとに全く異なるものになるため,モデル図の段階から因子の名前を変えておくのもアリだと思います。
あとは 図 9.32 をlavaanの文法に変換して推定するだけです。
マルチレベルモデルに含まれる潜在変数の名前は,レベルごとに異なっていても,同じでもどちらでも結果は変わりません。 ですが,先ほど説明したように因子の意味が大きく異なるため,名前を変えておくと良いかもしれません。が,自由です。
lavaan 0.6-20 ended normally after 62 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 20
Number of observations 5766
Number of clusters [school_id] 183
Model Test User Model:
Test statistic 96.860
Degrees of freedom 4
P-value (Chi-square) 0.000
Parameter Estimates:
Standard errors Standard
Information Observed
Observed information based on Hessian
Level 1 [within]:
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_1 =~
teach1 0.613 0.011 54.611 0.000 0.613 0.704
teach2 0.619 0.011 58.442 0.000 0.619 0.746
teach3 0.636 0.012 53.622 0.000 0.636 0.694
teach4 0.626 0.010 60.005 0.000 0.626 0.761
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.teach1 0.382 0.009 40.753 0.000 0.382 0.504
.teach2 0.306 0.008 36.937 0.000 0.306 0.444
.teach3 0.436 0.011 41.474 0.000 0.436 0.519
.teach4 0.285 0.008 35.473 0.000 0.285 0.421
f_1 1.000 1.000 1.000
Level 2 [school_id]:
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_2 =~
teach1 0.156 0.020 7.809 0.000 0.156 0.820
teach2 0.147 0.018 8.240 0.000 0.147 0.878
teach3 0.167 0.022 7.674 0.000 0.167 0.785
teach4 0.161 0.017 9.682 0.000 0.161 0.983
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.teach1 3.016 0.018 165.993 0.000 3.016 15.886
.teach2 3.181 0.017 192.116 0.000 3.181 18.995
.teach3 2.808 0.020 141.506 0.000 2.808 13.237
.teach4 3.171 0.016 195.077 0.000 3.171 19.419
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.teach1 0.012 0.003 3.803 0.000 0.012 0.327
.teach2 0.006 0.002 2.723 0.006 0.006 0.229
.teach3 0.017 0.004 4.472 0.000 0.017 0.383
.teach4 0.001 0.002 0.439 0.661 0.001 0.033
f_2 1.000 1.000 1.000得られた結果(Std.all)をモデル図に書き入れると 図 9.33 のようになります。 どちらのレベルについても,すべての項目に対して高い因子負荷量が得られており,基本的には1因子にまとまると考えて良さそうです。
ちなみに,Level 2 [school_id]:のVariances:の推定値を見るとわかるように,今回のマルチレベルCFAでは,レベル2の因子について,標準化する前の残差(独自因子の分散)は非常に小さくなっています。 これは,以下に示すように,teach1-4の学校ごとの平均値の分散は小さく,ICCが概ね0.05以下と非常に小さいためです。
その結果,teach1-4の共分散行列を「集団レベル」と「個人レベル」の分解した場合,「集団レベル」の共分散行列は,非常に小さな値となってしまいます。
# すべての変数間の共分散を明示するだけ
model <- "
level: 1
teach1 ~~ teach2 + teach3 + teach4
teach2 ~~ teach3 + teach4
teach3 ~~ teach4
level: 2
teach1 ~~ teach2 + teach3 + teach4
teach2 ~~ teach3 + teach4
teach3 ~~ teach4
"
model_cov <- sem(model, data = dat, cluster = "school_id")
# summary(model_cov, standardized = TRUE)実際にlavaanで推定した結果をもとに共分散行列を表示する場合,以下のようにして求めることができます。
$within
$within$cov
teach1 teach2 teach3 teach4
teach1 0.758
teach2 0.398 0.689
teach3 0.358 0.399 0.841
teach4 0.388 0.370 0.417 0.676
$within$mean
teach1 teach2 teach3 teach4
0 0 0 0
$school_id
$school_id$cov
teach1 teach2 teach3 teach4
teach1 0.036
teach2 0.024 0.028
teach3 0.024 0.024 0.045
teach4 0.025 0.023 0.027 0.027
$school_id$mean
teach1 teach2 teach3 teach4
3.016 3.181 2.808 3.171 それぞれのレベルの$covの出力が,レベルごとに分解された共分散行列を表しています。したがって, \[
\begin{alignedat}{2}
\mathrm{(レベル1)} & \quad &
\mathrm{Cov}\begin{bmatrix}
\mathrm{teach1} \\
\mathrm{teach2} \\
\mathrm{teach3} \\
\mathrm{teach4}
\end{bmatrix} = \begin{bmatrix}
0.758 & & & \\
0.398 & 0.689 & & \\
0.358 & 0.399 & 0.841 & \\
0.388 & 0.370 & 0.417 & 0.676
\end{bmatrix} \\
\mathrm{(レベル2)} & \quad &
\mathrm{Cov}\begin{bmatrix}
\mathrm{teach1} \\
\mathrm{teach2} \\
\mathrm{teach3} \\
\mathrm{teach4}
\end{bmatrix} = \begin{bmatrix}
0.036 & & & \\
0.024 & 0.028 & & \\
0.024 & 0.024 & 0.045 & \\
0.025 & 0.023 & 0.027 & 0.027
\end{bmatrix}
\end{alignedat}
\tag{9.69}\] となり,レベル2共分散行列の値がとても小さくなることが分かります。 一方で相関係数(Std.all列)は非常に大きいため,因子分析を行った際の因子負荷は大きな値になっています。 ここだけを見ると,マルチレベルCFAを行うことに十分な意味があるようにも見えてしまいますが,そもそものレベル2共分散行列の値がが小さくなってしまう(=ICCがいずれも小さい)ような場合には,わざわざマルチレベルにする意味は小さいのかもしれません。
9.5.4 マルチレベルSEM
最後は,因子分析と回帰分析(パス解析)を組み合わせたフルのSEMを実行してみましょう。 図 9.34 に,思いつきで大きなモデルを作成してみました。 このように,マルチレベルSEMではレベルごとに全く異なるモデルを構築することも可能です。
回帰分析の部分(オレンジの矢印)についての一応の仮説としては,
レベル1 :
- 学校内での相対的なESCSが高い生徒ほど,学校内に居場所を得ることができ(
escs -> f_B1),教師からも目をかけてもらいやすい(escs -> f_T1) - 所属感の高い生徒ほど,またしっかりと指導してもらっている生徒ほど読解力が高い(
f_B1 -> read_scoreおよびf_T1 -> read_score) - もちろん相対的にESCSが高い生徒ほど読解力は高い傾向にある(
escs -> read_score)
レベル2 :
- 教師の授業の構成力は,レベルの高い学校ほど(
escs -> f_T2),またST比が低く余裕のある学校ほど(s_t_ratio -> f_T2)高い傾向にある - 学校の読解力の平均値は,授業の構成力が高い学校ほど(
f_T2 -> read_score),またESCSの平均が高い学校ほど(escs -> read_score)高い傾向にある
といったことを想定しています。 根拠はありません。
ということで, 図 9.34 のモデルをlavaanで実行してみましょう。
model <- "
level: 1
f_T1 ~ escs
f_B1 ~ escs
f_T1 =~ teach1 + teach2 + teach3 + teach4
f_B1 =~ belong1 + belong2 + belong3 + belong4 + belong5 + belong6
read_score ~ f_T1 + f_B1 + escs
level: 2
f_T2 ~ escs + s_t_ratio
f_T2 =~ teach1 + teach2 + teach3 + teach4
read_score ~ f_T2 + escs
"
model_mlsem <- sem(model, data = dat, std.lv = TRUE, cluster = "school_id")Warning: lavaan->lav_data_full():
some observed variances are (at least) a factor 1000 times larger
than others; use varTable(fit) to investigatelavaan 0.6-20 ended normally after 181 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 50
Number of observations 5766
Number of clusters [school_id] 183
Model Test User Model:
Test statistic 3056.118
Degrees of freedom 63
P-value (Chi-square) 0.000
Parameter Estimates:
Standard errors Standard
Information Observed
Observed information based on Hessian
Level 1 [within]:
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_T1 =~
teach1 0.613 0.011 54.629 0.000 0.613 0.704
teach2 0.619 0.011 58.425 0.000 0.619 0.746
teach3 0.636 0.012 53.551 0.000 0.636 0.693
teach4 0.626 0.010 60.042 0.000 0.626 0.761
f_B1 =~
belong1 0.473 0.011 42.027 0.000 0.473 0.625
belong2 0.526 0.013 42.049 0.000 0.526 0.627
belong3 0.507 0.011 45.787 0.000 0.507 0.687
belong4 0.490 0.012 39.615 0.000 0.490 0.613
belong5 0.425 0.010 43.177 0.000 0.425 0.633
belong6 0.491 0.012 42.062 0.000 0.491 0.646
Regressions:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_T1 ~
escs 0.032 0.023 1.401 0.161 0.032 0.021
f_B1 ~
escs 0.029 0.024 1.242 0.214 0.029 0.019
read_score ~
f_T1 4.210 1.115 3.776 0.000 4.211 0.056
f_B1 -3.636 1.143 -3.183 0.001 -3.637 -0.049
escs 7.406 1.560 4.747 0.000 7.406 0.063
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.belong1 3.262 0.010 327.163 0.000 3.262 4.308
.belong2 2.845 0.011 257.493 0.000 2.845 3.391
.belong3 2.958 0.010 304.651 0.000 2.958 4.012
.belong4 3.072 0.011 291.657 0.000 3.072 3.841
.belong5 2.807 0.009 317.651 0.000 2.807 4.183
.belong6 3.304 0.010 329.648 0.000 3.304 4.341
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.teach1 0.382 0.009 40.780 0.000 0.382 0.504
.teach2 0.306 0.008 36.897 0.000 0.306 0.444
.teach3 0.437 0.011 41.530 0.000 0.437 0.520
.teach4 0.284 0.008 35.425 0.000 0.284 0.421
.belong1 0.350 0.009 38.133 0.000 0.350 0.610
.belong2 0.427 0.011 37.667 0.000 0.427 0.606
.belong3 0.287 0.009 31.962 0.000 0.287 0.528
.belong4 0.400 0.011 37.121 0.000 0.400 0.624
.belong5 0.270 0.007 38.162 0.000 0.270 0.600
.belong6 0.338 0.010 34.751 0.000 0.338 0.583
.read_score 5527.897 104.774 52.760 0.000 5527.897 0.990
.f_T1 1.000 1.000 1.000
.f_B1 1.000 1.000 1.000
Level 2 [school_id]:
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_T2 =~
teach1 0.154 0.020 7.744 0.000 0.154 0.814
teach2 0.148 0.018 8.088 0.000 0.148 0.879
teach3 0.162 0.022 7.475 0.000 0.163 0.774
teach4 0.163 0.016 9.900 0.000 0.163 0.991
Regressions:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f_T2 ~
escs -0.181 0.318 -0.569 0.570 -0.180 -0.063
s_t_ratio 0.006 0.021 0.289 0.773 0.006 0.029
read_score ~
f_T2 13.668 3.871 3.531 0.000 13.695 0.225
escs 143.842 9.130 15.755 0.000 143.842 0.823
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.teach1 3.002 0.045 67.361 0.000 3.002 15.857
.teach2 3.167 0.043 74.269 0.000 3.167 18.805
.teach3 2.793 0.047 58.998 0.000 2.793 13.288
.teach4 3.156 0.046 68.525 0.000 3.156 19.194
.read_score 518.476 4.838 107.178 0.000 518.476 8.531
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.teach1 0.012 0.003 3.918 0.000 0.012 0.338
.teach2 0.006 0.002 2.684 0.007 0.006 0.227
.teach3 0.018 0.004 4.605 0.000 0.018 0.401
.teach4 0.000 0.002 0.229 0.818 0.000 0.017
.read_score 1077.909 169.143 6.373 0.000 1077.909 0.292
.f_T2 1.000 0.996 0.996なお,レベル2にのみ投入する説明変数(上の例ではs_t_ratio)がある場合,その説明変数は集団ごとに全員に同じ値が入っていることを確認しておいてください。 例えばescsなど,個人ごとに異なる値が入っている説明変数がレベル2にのみ投入されている場合,以下のようなエラーが出て正しく推定が行われません。
Error: lavaan->lav_data_full():
Some between-level (only) variables have non-zero variance at the
within-level. Please double-check your data.また,個人ごとに値が異なる(レベル1の)変数については,
- レベル2のモデルに登場する場合は自動的に集団平均中心化のようなことが行われた後の値が使われる
- レベル2のモデルに登場しない場合はそのまま使われる
ことになるので気をつけておきましょう。
推定結果をモデル図の中で示したものが 図 9.35 です。 なお,この図では,因子分析の部分(青い矢印)についてはStd.all列の値を,回帰分析の部分(オレンジの矢印)についてはEstimate列の値を記しています。
因子分析の部分はいずれも問題なさそうなので,回帰分析の部分について結果を見ていくと,
レベル1 :
- 相対的な
escsと所属感および授業の構成の間にはほぼ関係がない一方で,直接read_scoreに正の影響を与えている(とはいえレベル2の係数と比べると小さい) - 所属感が高い生徒ほど
read_scoreは低い傾向にある
レベル2 :
- 授業の構成力に対して
escsおよびs_t_ratioはほぼ関係ない(そもそもf_T2の分散が小さいため,かもしれない) - 学校の平均
escsはもちろんのこと,授業の構成力f_T2もread_scoreに正の効果を持っている(ただしf_T2の分散が…)
といった感じになるでしょうか。 ただモデルに理論的な背景が無いので,これ以上の深読みはやめておきましょう。
現時点のlavaanのバージョン(2025/07/31時点で0.6-19)では,引数clusterとorderedを同時に指定することはできません。 すなわち,マルチレベル・カテゴリカルSEMを実施することはできません。 そのため,カテゴリカルな内生変数(wants_univなど)を含んだモデルを行う場合は,Mplusなどの別のソフトウェアを利用するか,諦めるしかないのが現状です。 一応lavaanの開発計画には”multilevel SEM with categorical data”の記載があるので,いつかは実装されるかもしれません。 気長に待ちましょう。
9.5.5 SEM的なモデルチェック
マルチレベルSEMを行うメリットに,SEM的なツールが色々と使える,という点が挙げられます。 チャプター 7 で見てきた中から,いくつかの関数を試してみましょう。
適合度指標
npar fmin chisq
50.000 6.367 3056.118
df pvalue baseline.chisq
63.000 0.000 29575.698
baseline.df baseline.pvalue cfi
86.000 0.000 0.899
tli nnfi rfi
0.861 0.861 0.859
nfi pnfi ifi
0.897 0.657 0.899
rni logl unrestricted.logl
0.899 -99917.457 -98389.398
aic bic ntotal
199934.914 200267.901 5766.000
bic2 rmsea rmsea.ci.lower
200109.015 0.091 0.088
rmsea.ci.upper rmsea.ci.level rmsea.pvalue
0.094 0.900 0.000
rmsea.close.h0 rmsea.notclose.pvalue rmsea.notclose.h0
0.050 1.000 0.080
srmr srmr_within srmr_between
0.198 0.075 0.123 もともと適当に作ったモデルであり,あまり意味のないレベル2因子があったり,有意ですらないパスが含まれていたりすることもあって,適合度はさほど良いとも言えません。 ただこのような感じで,モデル適合度の観点から,マルチレベルSEMを評価することが可能である,という点は階層線形モデルにはなかった利点と言えるでしょう。
fitMeasures()関数は,もちろん両方のレベルを合わせた適合度を算出するため,適合度が悪い場合には,どちらのレベルが悪いのか,あるいはどちらのレベルも悪いのかはわかりません。 このような場合には,レベルごとに適合度を評価することが有効となる可能性があります。
レベルごとの適合度を見るためには,「レベルごとのモデル」と「レベルごとの共分散行列(と平均ベクトル)」が必要となります。 ということで,まずは「レベルごとのモデル」を作成していきます。 といっても,これは単にlevel:で区切っていたモデルを別々に定義するだけです。
model_l1 <- "
# level: 1 に書いていた部分
f_T1 ~ escs
f_B1 ~ escs
f_T1 =~ teach1 + teach2 + teach3 + teach4
f_B1 =~ belong1 + belong2 + belong3 + belong4 + belong5 + belong6
read_score ~ f_T1 + f_B1 + escs
"
model_l2 <- "
# level: 2 に書いていた部分
f_T2 ~ escs + s_t_ratio
f_T2 =~ teach1 + teach2 + teach3 + teach4
read_score ~ f_T2 + escs
"そして,「レベルごとの共分散行列(と平均ベクトル)」は,以下のようにして求めることができます。
$within
$within$cov
teach1 teach2 teach3 teach4 belng1 belng2 belng3
teach1 0.760
teach2 0.400 0.691
teach3 0.360 0.401 0.843
teach4 0.389 0.372 0.419 0.677
belong1 0.052 0.063 0.037 0.060 0.573
belong2 0.034 0.050 0.042 0.034 0.190 0.704
belong3 0.069 0.078 0.064 0.067 0.187 0.359 0.543
belong4 0.074 0.081 0.068 0.066 0.313 0.178 0.195
belng4 belng5 belng6 rd_scr escs
teach1
teach2
teach3
teach4
belong1
belong2
belong3
belong4 0.640
[ reached 'max' / getOption("max.print") -- omitted 4 rows ]
$within$mean
teach1 teach2 teach3 teach4 belong1 belong2
0.000 0.000 0.000 0.000 3.262 2.845
belong3 belong4 belong5 belong6 read_score escs
2.958 3.072 2.807 3.304 0.000 0.000
$school_id
$school_id$cov
teach1 teach2 teach3 teach4 rd_scr escs s_t_rt
teach1 0.033
teach2 0.019 0.022
teach3 0.020 0.020 0.041
teach4 0.022 0.019 0.024 0.023
read_score -1.441 2.902 -1.815 1.086 3600.641
escs -0.018 0.009 -0.020 -0.005 17.080 0.121
s_t_ratio -0.130 0.092 -0.083 -0.045 81.545 0.385 22.260
$school_id$mean
teach1 teach2 teach3 teach4 read_score escs
3.018 3.180 2.810 3.172 503.492 -0.113
s_t_ratio
11.950 lavInspect("h1")は,推定されたモデルパラメータに基づいてレベル別の共分散行列と平均ベクトルを計算してくれる関数です。
あとは,上記の情報を使ってレベルごとに再度lavaanを実行するだけです。 lavaanの関数は,データを丸ごと与える他に(psych::fa()関数などもそうであったように)「共分散行列(sample.cov)」「平均ベクトル(sample.mean)」「サンプルサイズ(sample.nobs)」を与えることでもパラメータ推定を行うことができます。
# レベル1の部分だけの推定
model_mlsem_l1 <- sem(model_l1,
std.lv = TRUE,
sample.cov = cov_mean$within$cov,
sample.mean = cov_mean$within$mean,
sample.nobs = nrow(dat)
)
# レベル2の部分だけの推定
model_mlsem_l2 <- sem(model_l2,
std.lv = TRUE,
sample.cov = cov_mean$school_id$cov,
sample.mean = cov_mean$school_id$mean,
sample.nobs = 183 # レベル2の集団数
)レベルごとに推定された結果29をもとに適合度を見てみましょう。
今回はどちらも大して良くないようですが,その中でもレベル2のほうがなおさら適合度が悪いようです。 ただ何度も見ているように,そもそもレベル2の共分散行列は値が小さいので,これ以上の深追いはやめておきましょう。
モデル修正
lhs op rhs block group level mi epc sepc.lv sepc.all
129 belong4 ~~ belong6 1 1 1 919.872 0.186 0.186 0.506
119 belong2 ~~ belong3 1 1 1 725.070 0.167 0.167 0.477
125 belong3 ~~ belong5 1 1 1 575.525 0.119 0.119 0.428
117 belong1 ~~ belong6 1 1 1 481.375 0.127 0.127 0.370
115 belong1 ~~ belong4 1 1 1 423.871 0.126 0.126 0.337
120 belong2 ~~ belong4 1 1 1 337.055 -0.124 -0.124 -0.301
126 belong3 ~~ belong6 1 1 1 334.642 -0.103 -0.103 -0.331
131 belong5 ~~ belong6 1 1 1 307.838 -0.090 -0.090 -0.298
114 belong1 ~~ belong3 1 1 1 286.407 -0.095 -0.095 -0.299
sepc.nox
129 0.506
119 0.477
125 0.428
117 0.370
115 0.337
120 -0.301
126 -0.331
131 -0.298
114 -0.299
[ reached 'max' / getOption("max.print") -- omitted 89 rows ]modindices()関数も,マルチレベルSEMで利用可能なはずです。 出力を見ると,levelという列30が増えています。 この列が,どのレベルのモデルについての修正の提案であるかを表しているわけです。 ただ今回の結果は,上位がbelongの項目間に誤差共分散をつけるものばかりが提案されており,あまり意味のある修正は見られなさそうです……。
9.5.6 別のアプローチ
ここまでに解説したマルチレベルSEMの考え方では,階層線形モデルでいうところのランダム傾きモデルなど,集団ごとに回帰係数が異なるようなモデルを表現することができません31。 そこで,近年では別のアプローチによるマルチレベルSEM (Mehta & Neale, 2005) を使うことが増えてきているようです (尾崎 他,2019)。
これ以降の内容は,Rではまだあまり十分に実装されていません。 考え方および「現状はこんなことなら出来る」という説明にとどまります。 なお,高度なモデルをガッツリ実行したい場合には,Mplusという有償のソフトウェアを利用するのがおすすめです。
回帰式を因子分析的に表す
改めて,最もシンプルなランダム切片モデルの式(9.8)を見てみます。 \[ \begin{alignedat}{2} \text{(レベル1)} \quad & y_{pg} & & = \beta_{0g} + u_{pg} \\ \text{(レベル2)} \quad & \beta_{0g} & & = \mu + u_{0g} \end{alignedat} \] この式は,ある個人の\(y_{pg}\)の値が,「集団\(g\)に共通の平均値\(\beta_{0g}\)」と「個人ごとに異なる\(u_{pg}\)」の2つによって決まっていることを表していました。 したがって,集団\(g\)の中の複数人の\(y_{pg}\)の値は,以下のように表すことができます。
\[ \begin{aligned} y_{1g} & = \beta_{0g} + u_{1g} \\ y_{2g} & = \beta_{0g} + u_{2g} \\ \vdots \\ y_{n_gg} & = \beta_{0g} + u_{n_gg} \end{aligned} \]
この式を(少し強引に見えるかもしれませんが)因子分析モデルに無理やり当てはめてみると, 図 9.36 のように表すことができます。
一つずつ見ていくと,
- 集団\(g\)の全員に同じ値をもたらすために,集団の切片\(\beta_{0g}\)を全員に共通の因子負荷(通常は1)でかける
- 個人ごとの値の違いは,独自因子として与える
- 独自因子の分布は全員,そして全集団で共通(\(u_{pg} \sim N(0, \sigma^2_{pg})\))
という感じです。 因子分析では,個人の共通因子の得点を,複数の観測変数から求めていました。 ランダム切片モデルでも,各集団\(g\)の共通因子に当たる\(\beta_{0g}\)の値を,その集団に所属する複数の個人の\(y_{pg}\)の値から求めている,と考えると全く同じことなのです。
ということでランダム切片モデルは,適切な制約のもとでは,観測変数の数が\(n_g\)個の一因子モデルとして表すことができます32。 ただし,この方法は基本的には欠測がない,すなわち各集団のサンプルサイズがすべて同じ場合に適用可能な方法です。 ……なのですが,幸いなことにSEMにおいては,欠測がある場合の対処法がすでに確立されています。 簡単に言うと,「データがあるところだけを使って最尤推定を行う」完全情報最尤推定(full information maximul likelihood [FIML])という方法があり,lavaan(やMplusなど)にすでに実装されています。
ということで,無理やり因子分析のようにしてランダム切片モデルを試してみましょう。 このためには,まずデータを各行が集団になるように変換する必要があります。 その方法は色々ある33のですが,ここではreshapeという関数を使ってみます。
# まずは集団内に連番をつける(あとで使うため)
dat$id_in_group <- ave(dat$student_id, dat$school_id, FUN = seq_along)
# wide型に変換する
dat_wide <- reshape(dat,
idvar = "school_id", # wide型にしたときの行
timevar = "id_in_group", # wide型にしたときの列
v.names = "read_score", # wide型にしたときの値
direction = "wide" # wide型に変換する,という宣言
)
# 使う行だけ残す
col_use <- grep("read_score", colnames(dat_wide))
dat_wide <- dat_wide[, col_use]
# 列名の変更,このあとのことを考えてできるだけ短くしたい
colnames(dat_wide) <- paste0("x", seq_along(col_use))
head(dat_wide) x1 x2 x3 x4 x5 x6 x7 x8
1 704.541 569.687 647.678 672.170 671.836 770.257 629.302 635.377
36 407.067 516.066 476.785 481.392 487.458 463.513 297.027 525.794
70 394.599 377.281 320.707 596.066 550.053 503.949 549.370 401.773
98 481.432 633.283 606.886 465.688 540.154 475.517 482.591 522.945
131 417.018 463.160 484.525 557.468 361.538 434.686 325.217 473.500
162 656.984 658.027 558.086 541.708 600.806 648.765 699.864 583.038
x9 x10 x11 x12 x13 x14 x15 x16
1 569.792 629.565 558.669 710.876 678.167 572.808 555.934 630.040
36 472.075 525.836 562.182 413.959 525.294 486.594 523.139 520.569
70 433.376 435.975 584.493 524.617 284.713 511.741 466.476 419.863
98 615.102 397.207 517.198 559.928 402.294 421.546 367.346 579.669
131 341.105 402.302 388.488 449.652 120.788 563.629 391.874 452.526
162 599.655 682.270 668.412 592.554 565.286 612.133 597.207 531.676
x17 x18 x19 x20 x21 x22 x23 x24
1 554.016 623.540 560.076 567.106 687.581 685.917 674.400 566.263
36 526.796 559.321 445.163 471.139 425.071 384.130 424.149 402.880
70 607.630 417.726 374.933 428.235 392.184 601.386 535.630 531.243
98 425.272 541.008 546.868 471.983 469.782 454.392 611.397 454.496
131 432.385 241.960 356.772 542.058 338.747 465.785 441.305 345.869
162 579.109 651.421 532.560 724.961 552.878 551.477 715.887 675.034
x25 x26 x27 x28 x29 x30 x31 x32
1 692.116 530.061 642.351 664.494 510.211 657.856 722.404 524.830
36 399.164 400.898 388.972 535.431 499.609 620.378 582.890 392.931
70 452.884 552.959 389.370 284.715 NA NA NA NA
98 601.194 558.166 536.509 575.462 596.815 418.474 465.308 446.476
131 536.040 376.222 386.487 383.930 390.537 358.121 439.226 NA
162 638.978 605.978 601.015 654.758 621.334 449.931 614.251 639.797
x33 x34 x35
1 525.987 484.467 663.052
36 449.216 485.054 NA
70 NA NA NA
98 446.658 NA NA
131 NA NA NA
162 587.172 NA NA出来上がったデータフレームは,各行が異なる学校(school_id)を表しています。 そして列数が「最も人数の多い集団\(g\)の数」に一致し,それよりも人数が少ない集団については残りがNAで埋められた形になっています。
ave()関数は,指定したグループごとに同じ関数を適用できる関数です。 例えば,以下のように書くと,read_scoreの学校ごとの分散を計算してくれます。
ave] グループごとに同じ関数を適用する
[1] 4897.726 4897.726 4897.726 4897.726 4897.726 4897.726 4897.726
[8] 4897.726 4897.726 4897.726 4897.726 4897.726 4897.726 4897.726
[15] 4897.726 4897.726 4897.726 4897.726 4897.726 4897.726 4897.726
[22] 4897.726 4897.726 4897.726 4897.726 4897.726 4897.726 4897.726
[29] 4897.726 4897.726 4897.726 4897.726 4897.726 4897.726 4897.726
[36] 4670.416 4670.416 4670.416 4670.416 4670.416 4670.416 4670.416
[43] 4670.416 4670.416 4670.416 4670.416 4670.416 4670.416 4670.416
[50] 4670.416 4670.416 4670.416 4670.416 4670.416 4670.416 4670.416
[57] 4670.416 4670.416 4670.416 4670.416 4670.416 4670.416 4670.416
[64] 4670.416 4670.416 4670.416 4670.416 4670.416 4670.416 8815.489
[71] 8815.489 8815.489 8815.489 8815.489 8815.489 8815.489 8815.489
[78] 8815.489 8815.489 8815.489 8815.489 8815.489 8815.489 8815.489
[85] 8815.489 8815.489 8815.489 8815.489 8815.489 8815.489 8815.489
[92] 8815.489 8815.489 8815.489 8815.489 8815.489 8815.489 5353.813
[99] 5353.813 5353.813
[ reached 'max' / getOption("max.print") -- omitted 5666 entries ]ave()関数のポイントは,出力がもとのベクトルと同じ長さになるという点です。 つまり,上のコードを実行すると,dat$school_id == "001"のところには,全員分同じ値(read_scoreの分散)が返ってくることになります。
そして,seq_along()関数は,与えた引数の長さと同じ長さの整数の配列を返してくれます。
seq_along] 同じ長さの整数の配列を返す
ということで,以上を組み合わせると,school_idごとに通し番号を振ることができるのです。
aveとseq_alongを組み合わせる
[1] "1" "2" "3" "4" "5" "6" "7" "8" "9" "10" "11" "12" "13" "14"
[15] "15" "16" "17" "18" "19" "20" "21" "22" "23" "24" "25" "26" "27" "28"
[29] "29" "30" "31" "32" "33" "34" "35" "1" "2" "3" "4" "5" "6" "7"
[43] "8" "9" "10" "11" "12" "13" "14" "15" "16" "17" "18" "19" "20" "21"
[57] "22" "23" "24" "25" "26" "27" "28" "29" "30" "31" "32" "33" "34" "1"
[71] "2" "3" "4" "5" "6" "7" "8" "9" "10" "11" "12" "13" "14" "15"
[85] "16" "17" "18" "19" "20" "21" "22" "23" "24" "25" "26" "27" "28" "1"
[99] "2" "3"
[ reached 'max' / getOption("max.print") -- omitted 5666 entries ]続いてgrep()は,character型ベクトルの中から,特定の文字列を含んでいる要素の番号を探してくれます。
grep] 文字列が一致する要素の場所を教える
したがって,grep("read_score",colnames(dat_wide))という指示は,「dat_wideの中で列名にread_scoreが入っている列番号を教えて」という意味になり,これを列番号に指定することでread_scoreの部分だけが残ったデータフレームが作れるのです。
あとはlavaanのモデル式を書くだけです。 が,制約(因子負荷はすべて1,独自因子の分散はすべて共通,独自因子の平均値はすべて0)を満たすように書くのがかなり大変です。
最終的に,出来上がったコードは以下のようになります。
model <- "
# 共通因子(ランダム切片)の部分
beta_0g =~ 1*x1 + 1*x2 + 1*x3 + 1*x4 + 1*x5 + 1*x6 +
1*x7 + 1*x8 + 1*x9 + 1*x10 + 1*x11 + 1*x12 +
1*x13 + 1*x14 + 1*x15 + 1*x16 + 1*x17 + 1*x18 +
1*x19 + 1*x20 + 1*x21 + 1*x22 + 1*x23 + 1*x24 +
1*x25 + 1*x26 + 1*x27 + 1*x28 + 1*x29 + 1*x30 +
1*x31 + 1*x32 + 1*x33 + 1*x34 + 1*x35
# 独自因子(個人レベル変量効果)の部分
x1 ~~ u*x1; x2 ~~ u*x2; x3 ~~ u*x3; x4 ~~ u*x4; x5 ~~ u*x5;
x6 ~~ u*x6; x7 ~~ u*x7; x8 ~~ u*x8; x9 ~~ u*x9; x10 ~~ u*x10;
x11 ~~ u*x11; x12 ~~ u*x12; x13 ~~ u*x13; x14 ~~ u*x14; x15 ~~ u*x15;
x16 ~~ u*x16; x17 ~~ u*x17; x18 ~~ u*x18; x19 ~~ u*x19; x20 ~~ u*x20;
x21 ~~ u*x21; x22 ~~ u*x22; x23 ~~ u*x23; x24 ~~ u*x24; x25 ~~ u*x25;
x26 ~~ u*x26; x27 ~~ u*x27; x28 ~~ u*x28; x29 ~~ u*x29; x30 ~~ u*x30;
x31 ~~ u*x31; x32 ~~ u*x32; x33 ~~ u*x33; x34 ~~ u*x34; x35 ~~ u*x35
# beta_0gの平均と分散を推定してもらう
beta_0g ~~ beta_0g
beta_0g ~ 1
"モデル式をすべて手書きで行うのはどう考えても面倒かつミスが起こりやすいので,paste0()などの関数を使ってラクをしましょう。 これまでも複数の列名を指定するときに使用してきたように,paste0()の引数にベクトルを与えると,そのベクトルを展開して文字列ベクトルを作ってくれます。
ここで便利なのが,引数collapseです。 これを指定すると,collapseで指定した文字列を間に挟みながら,全体を一つの文字列として返してくれるようになります。
ということで,以下のようにしてモデル式の一部を作成し,これをコピペすると,多少は楽になるかと思います。
lavaanのモデル式の一部を自動的に作成
[1] "1*x1 + 1*x2 + 1*x3 + 1*x4 + 1*x5 + 1*x6 + 1*x7 + 1*x8 + 1*x9 + 1*x10 + 1*x11 + 1*x12 + 1*x13 + 1*x14 + 1*x15 + 1*x16 + 1*x17 + 1*x18 + 1*x19 + 1*x20 + 1*x21 + 1*x22 + 1*x23 + 1*x24 + 1*x25 + 1*x26 + 1*x27 + 1*x28 + 1*x29 + 1*x30 + 1*x31 + 1*x32 + 1*x33 + 1*x34 + 1*x35"
[1] "x1 ~~ u*x1; x2 ~~ u*x2; x3 ~~ u*x3; x4 ~~ u*x4; x5 ~~ u*x5; x6 ~~ u*x6; x7 ~~ u*x7; x8 ~~ u*x8; x9 ~~ u*x9; x10 ~~ u*x10; x11 ~~ u*x11; x12 ~~ u*x12; x13 ~~ u*x13; x14 ~~ u*x14; x15 ~~ u*x15; x16 ~~ u*x16; x17 ~~ u*x17; x18 ~~ u*x18; x19 ~~ u*x19; x20 ~~ u*x20; x21 ~~ u*x21; x22 ~~ u*x22; x23 ~~ u*x23; x24 ~~ u*x24; x25 ~~ u*x25; x26 ~~ u*x26; x27 ~~ u*x27; x28 ~~ u*x28; x29 ~~ u*x29; x30 ~~ u*x30; x31 ~~ u*x31; x32 ~~ u*x32; x33 ~~ u*x33; x34 ~~ u*x34; x35 ~~ u*x35"そして,こういったラクをするためにも,データを作成する際には変数名には明確なルールを設けて体系的に管理するのがおすすめです。
コードが書けたら,あとは推定を実行するだけです。 lavaanは,デフォルトでは欠測がある行はリストワイズ削除する仕様になっています。 欠測を無視して先ほど紹介したFIMLを実行してもらうためには,missing="fiml"を指定する必要があります。
lavaan 0.6-19 ended normally after 73 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 37
Number of equality constraints 34
Number of observations 183
Number of missing patterns 17
(中略)
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
beta_0g =~
x1 1.000 60.161 0.629
x2 1.000 60.161 0.629
(中略)
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
beta_0g 503.699 4.562 110.401 0.000 8.367 8.367
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.x1 (u) 5579.473 105.605 52.833 0.000 5579.473 0.606
.x2 (u) 5579.473 105.605 52.833 0.000 5579.473 0.606
(中略)
.x35 (u) 5579.473 105.605 52.833 0.000 5579.473 0.606
beta_0g 3624.390 398.532 9.094 0.000 1.000 1.000正しく因子負荷を1に固定できていれば,Latent Variables:の推定値はすべて1になっているはずです。 そしてIntercepts:のbeta_0gの推定値(503.699)が,切片の全体平均\(\mu\)に相当します。 また,Variances:はそれぞれの分散成分を表しており,すべての観測変数に共通のuの値(5579.473)が個人レベルの分散を,またbeta_0gの値(3624.390)が,集団レベルの分散を表しています。 これらの値は,すべて説明変数のないランダム切片モデルをglmmTMB()で推定したとき(summary(model0)の出力)と全く同じ値になっており,確かに同一のモデルをマルチレベルSEMの枠組みで表せることが分かります。
ランダム傾きモデル
続いては,集団ごとに傾きも異なるモデルを考えてみます。 本当は説明変数が連続変数の場合も簡単に実装できるとよいのですが,現状のlavaanでは相当難しいと思われるので,ここでは二値の説明変数に対するランダム傾きモデルを考えていきます。 ということで,説明変数を「escsが全体平均以上か」とし,被説明変数は変わらずread_scoreとします。 これは,「ESCSが高い生徒ほど読解力が高いのか」を検証するモデルをかなり簡略化したものになります(本当は集団レベルの効果を分離する必要があるのですが……)。
このとき,回帰式は(9.70)式にあったように \[ \begin{alignedat}{2} \text{(レベル1)} \quad & y_{pg} & & = \beta_{0g} +\beta_{1g}x_{pg}+ u_{pg} \\ \text{(レベル2)} \quad & \beta_{0g} & & = \mu + u_{0g}\\ \text{(レベル2)} \quad & \beta_{1g} & & = \beta_1 + u_{1g} \end{alignedat} \tag{9.70}\] と設定されていました。 ここでのポイントは,説明変数\(x_{pg}\)が二値(0または1)であるならば,レベル1の回帰式は\(x_{pg}\)の値によって場合分けして書ける,という点です。 具体的には, \[ y_{pg} =\begin{cases} \beta_{0g} + u_{pg} & (x_{pg}=0) \\ \beta_{0g} +\beta_{1g}+ u_{pg} & (x_{pg}=1) \end{cases} \tag{9.71}\] となります。 すなわち,傾き\(\beta_{1g}\)は,「\(x_{pg}=1\)の人にだけ共通で同じ値が追加される」という働きをしているのです。
そして変量効果は(9.38)式によって \[ \begin{alignedat}{2} \text{(レベル1)} &u_{pg} &&\sim N(0, \sigma^2_{pg}) \\ \text{(レベル2)} &\left[\begin{array}{c} u_{0g} \\ u_{1g} \end{array}\right] &&\sim MVN\left( \left[\begin{array}{c} 0 \\ 0 \end{array}\right], \left[\begin{array}{cc} \sigma_{0g}^2 & \sigma_{(0g)(1g)} \\ \sigma_{(0g)(1g)} & \sigma_{1g}^2 \end{array}\right]\right) \end{alignedat} \tag{9.72}\] と設定されていました。 以上のモデルを,再び無理やり因子分析の形で表すとしたら,「\(x_{pg}=1\)のひとにだけ切片項が追加される」と考えたら良いので, 図 9.37 のように表すことができます。
(かなり強引に見えるかもしれませんが)このモデルでは,すべての人に対して「\(x_{pg}=0\)のとき」と「\(x_{pg}=1\)のとき」を並列させて表しています。 すなわち,\(y_{pg}\)のとある人がいたときに,この人が\(x_{pg}=0\)であるならば\(y_{pg}^{(0)}=y_{pg}\)とし,\(y_{pg}^{(1)}\)は欠測とします。 SEMでは,欠測があってもFIMLによって無視することができたので,これによって共通因子の推定が可能になるのです。 ということで,二値の説明変数に対するランダム傾きモデルを実行するには,まずデータを横に2倍にする必要があります。 ということで,ここからは以下の手順でデータを再度整形します。
dat_wideと同じサイズで,escs_binもwide型に変換するdat_wideを2つ複製する
escs_bin == 1の要素に対応するdat_wideの要素をNAに置き換えたものescs_bin == 0の要素に対応するdat_wideの要素をNAに置き換えたもの
- で作った2つのデータフレームを横にくっつける
escs_binをwide型にする
# read_scoreにやったのと同じ手順で
dat_wide_escs <- reshape(dat,
idvar = "school_id", # wide型にしたときの行
timevar = "id_in_group", # wide型にしたときの列
v.names = "escs_bin", # wide型にしたときの値
direction = "wide" # wide型に変換する,という宣言
)
# 使う行だけ残す
col_e <- grep("escs_bin", colnames(dat_wide_escs))
dat_wide_escs <- dat_wide_escs[, col_e]
# 列名の変更
colnames(dat_wide_escs) <- paste0("b", seq_along(col_e))
head(dat_wide_escs) b1 b2 b3 b4 b5 b6 b7 b8 b9 b10 b11 b12 b13 b14 b15 b16 b17 b18 b19 b20
1 1 1 0 1 0 1 0 1 1 1 1 1 1 1 1 1 1 0 0 0
36 0 0 0 0 0 0 1 0 1 1 0 1 1 0 0 1 1 1 0 0
70 0 0 0 1 1 1 1 1 1 0 0 1 0 0 1 0 1 1 0 0
98 1 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 1 1 0 0
131 1 0 0 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0
162 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 0 1 1 0 1
b21 b22 b23 b24 b25 b26 b27 b28 b29 b30 b31 b32 b33 b34 b35
1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1
36 1 0 0 0 0 1 0 0 0 0 0 1 0 0 NA
70 1 1 0 1 0 1 0 0 NA NA NA NA NA NA NA
98 0 1 1 1 1 1 1 0 0 1 0 0 0 NA NA
131 1 0 0 0 0 1 0 0 1 0 0 NA NA NA NA
162 0 1 1 0 1 1 1 1 1 1 0 0 1 NA NA x1 x2 x3 x4 x5 x6 x7 x8 x9 x10
1 NA NA 647.678 NA 671.836 NA 629.302 NA NA NA
36 407.067 516.066 476.785 481.392 487.458 463.513 NA 525.794 NA NA
x11 x12 x13 x14 x15 x16 x17 x18 x19 x20 x21
1 NA NA NA NA NA NA NA 623.54 560.076 567.106 NA
36 562.182 NA NA 486.594 523.139 NA NA NA 445.163 471.139 NA
x22 x23 x24 x25 x26 x27 x28 x29 x30
1 NA NA NA NA NA NA NA NA NA
36 384.13 424.149 402.88 399.164 NA 388.972 535.431 499.609 620.378
x31 x32 x33 x34 x35
1 NA NA NA 484.467 NA
36 582.89 NA 449.216 485.054 NA
[ reached 'max' / getOption("max.print") -- omitted 4 rows ]
x36 x37 x38 x39 x40 x41 x42 x43 x44 x45
1 704.541 569.687 NA 672.17 NA 770.257 NA 635.377 569.792 629.565
36 NA NA NA NA NA NA 297.027 NA 472.075 525.836
x46 x47 x48 x49 x50 x51 x52 x53 x54 x55
1 558.669 710.876 678.167 572.808 555.934 630.040 554.016 NA NA NA
36 NA 413.959 525.294 NA NA 520.569 526.796 559.321 NA NA
x56 x57 x58 x59 x60 x61 x62 x63 x64
1 687.581 685.917 674.4 566.263 692.116 530.061 642.351 664.494 510.211
36 425.071 NA NA NA NA 400.898 NA NA NA
x65 x66 x67 x68 x69 x70
1 657.856 722.404 524.830 525.987 NA 663.052
36 NA NA 392.931 NA NA NA
[ reached 'max' / getOption("max.print") -- omitted 4 rows ]出来上がったdat_wide2を見ると,確かに対応するx1-x36,x2-x37,x3-x38,…はいずれも,どちら一方にのみ値が入っていることが分かります。 ということで,あとはlavaanのモデル式を書くだけです。 もちろん書かなければ行けない量は単純計算でも2倍になります。
model <- "
# 切片の共通因子(ランダム切片)の部分
beta_0g =~ 1*x1 + 1*x2 + 1*x3 + 1*x4 + 1*x5 +
1*x6 + 1*x7 + 1*x8 + 1*x9 + 1*x10 + 1*x11 +
1*x12 + 1*x13 + 1*x14 + 1*x15 + 1*x16 + 1*x17 + 1*x18 +
1*x19 + 1*x20 + 1*x21 + 1*x22 + 1*x23 + 1*x24 + 1*x25 +
1*x26 + 1*x27 + 1*x28 + 1*x29 + 1*x30 + 1*x31 + 1*x32 +
1*x33 + 1*x34 + 1*x35 + 1*x36 + 1*x37 + 1*x38 + 1*x39 +
1*x40 + 1*x41 + 1*x42 + 1*x43 + 1*x44 + 1*x45 + 1*x46 +
1*x47 + 1*x48 + 1*x49 + 1*x50 + 1*x51 + 1*x52 + 1*x53 +
1*x54 + 1*x55 + 1*x56 + 1*x57 + 1*x58 + 1*x59 + 1*x60 +
1*x61 + 1*x62 + 1*x63 + 1*x64 + 1*x65 + 1*x66 + 1*x67 +
1*x68 + 1*x69 + 1*x70
# 傾きの共通因子(ランダム傾き)の部分
# x_pg==1の部分(後半だけ)にかかる
beta_1g =~ 1*x36 + 1*x37 + 1*x38 + 1*x39 + 1*x40 +
1*x41 + 1*x42 + 1*x43 + 1*x44 + 1*x45 + 1*x46 +
1*x47 + 1*x48 + 1*x49 + 1*x50 + 1*x51 + 1*x52 +
1*x53 + 1*x54 + 1*x55 + 1*x56 + 1*x57 + 1*x58 +
1*x59 + 1*x60 + 1*x61 + 1*x62 + 1*x63 + 1*x64 +
1*x65 + 1*x66 + 1*x67 + 1*x68 + 1*x69 + 1*x70
# 独自因子(個人レベル変量効果)の部分
x1 ~~ u*x1; x2 ~~ u*x2; x3 ~~ u*x3; x4 ~~ u*x4; x5 ~~ u*x5;
x6 ~~ u*x6; x7 ~~ u*x7; x8 ~~ u*x8; x9 ~~ u*x9; x10 ~~ u*x10;
x11 ~~ u*x11; x12 ~~ u*x12; x13 ~~ u*x13; x14 ~~ u*x14; x15 ~~ u*x15;
x16 ~~ u*x16; x17 ~~ u*x17; x18 ~~ u*x18; x19 ~~ u*x19; x20 ~~ u*x20;
x21 ~~ u*x21; x22 ~~ u*x22; x23 ~~ u*x23; x24 ~~ u*x24; x25 ~~ u*x25;
x26 ~~ u*x26; x27 ~~ u*x27; x28 ~~ u*x28; x29 ~~ u*x29; x30 ~~ u*x30;
x31 ~~ u*x31; x32 ~~ u*x32; x33 ~~ u*x33; x34 ~~ u*x34; x35 ~~ u*x35;
x36 ~~ u*x36; x37 ~~ u*x37; x38 ~~ u*x38; x39 ~~ u*x39; x40 ~~ u*x40;
x41 ~~ u*x41; x42 ~~ u*x42; x43 ~~ u*x43; x44 ~~ u*x44; x45 ~~ u*x45;
x46 ~~ u*x46; x47 ~~ u*x47; x48 ~~ u*x48; x49 ~~ u*x49; x50 ~~ u*x50;
x51 ~~ u*x51; x52 ~~ u*x52; x53 ~~ u*x53; x54 ~~ u*x54; x55 ~~ u*x55;
x56 ~~ u*x56; x57 ~~ u*x57; x58 ~~ u*x58; x59 ~~ u*x59; x60 ~~ u*x60;
x61 ~~ u*x61; x62 ~~ u*x62; x63 ~~ u*x63; x64 ~~ u*x64; x65 ~~ u*x65;
x66 ~~ u*x66; x67 ~~ u*x67; x68 ~~ u*x68; x69 ~~ u*x69; x70 ~~ u*x70
# beta_0gの平均と分散を推定してもらう
beta_0g ~~ beta_0g
beta_0g ~ 1
# beta_1gの平均と分散を推定してもらう
beta_1g ~~ beta_1g
beta_1g ~ 1
# 2つの変量効果の共分散も
beta_0g ~~ beta_1g
"あとは推定するだけです。
lavaan 0.6-19 ended normally after 84 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 75
Number of equality constraints 69
Number of observations 183
Number of missing patterns 183
(中略)
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
beta_0g =~
x1 1.000 58.417 0.619
x2 1.000 58.417 0.619
(中略)
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
beta_0g ~~
beta_1g -286.049 193.804 -1.476 0.140 -0.235 -0.235
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
beta_0g 498.215 4.599 108.341 0.000 8.529 8.529
beta_1g 10.791 2.694 4.005 0.000 0.518 0.518
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.x1 (u) 5498.249 105.593 52.070 0.000 5498.249 0.617
.x2 (u) 5498.249 105.593 52.070 0.000 5498.249 0.617
(中略)
.x70 (u) 5498.249 105.593 52.070 0.000 5498.249 0.627
beta_0g 3412.513 404.971 8.427 0.000 1.000 1.000
beta_1g 434.654 162.727 2.671 0.008 1.000 1.000そしてこの結果も,やはりglmmTMB()で推定した場合とだいたい同じ値になります。
glmmTMB()で推定
Warning in finalizeTMB(TMBStruc, obj, fit, h, data.tmb.old): Model
convergence problem; non-positive-definite Hessian matrix. See
vignette('troubleshooting') Family: gaussian ( identity )
Formula: read_score ~ escs_bin + (escs_bin | school_id)
Data: dat
AIC BIC logLik -2*log(L) df.resid
NA NA NA NA 5760
Random effects:
Conditional model:
Groups Name Variance Std.Dev. Corr
school_id (Intercept) 3476.285 58.9600
escs_bin 0.634 0.7963 -0.95
Residual 5567.444 74.6153
Number of obs: 5766, groups: school_id, 183
Dispersion estimate for gaussian family (sigma^2): 5.57e+03
Conditional model:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 498.621 4.626 107.79 < 2e-16 ***
escs_bin 10.148 2.191 4.63 3.62e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1説明変数の数が増えた場合も,理論上は同じ要領で対応可能です。 例えば二値の説明変数が2つある場合には,「\((x_1,x_2)=(0,0)\)のとき」「\((x_1,x_2)=(0,1)\)のとき」「\((x_1,x_2)=(1,0)\)のとき」「\((x_1,x_2)=(1,1)\)のとき」という4つの状態を用意して,それぞれ対応するところにだけ傾き因子を因子負荷1で与えたら良いのです。 同様に,説明変数が多値の場合(リッカート尺度など)であっても,「\(x_{pg}=0\)のとき」「\(x_{pg}=1\)のとき」「\(x_{pg}=2\)のとき」……という形で,カテゴリ数と同じ数の状態を用意してあげると,理論上は対応可能です。 実際にやるとなると,コードを書くのが非常に大変になったり,推定もうまく行かなくなってくるかもしれません。
ただ,それだけ頑張ったとしても,得られる結果は基本的にglmmTMB()(やlmer())でも推定可能なものです。 ということで,もうお分かりかと思いますが,この考え方でマルチレベルSEMを実行する場合,lavaanでできる範囲のことはglmmTMB()でほとんど事足りてしまいます。 現時点では,lavaanでマルチレベルSEMを行う場合は,本節の前半で紹介した「共分散行列を分解する」考え方に則って,level:を使って行うのがおすすめと言えるかもしれません。 そして,もっとしっかりと分析したければ,Mplusに手を出しましょう。
9.6 マルチレベル項目反応理論(未完成)
(sirtパッケージのmcmc.2pno.ml()を使うと良さそう,ただMCMCの理解が必要そう)
ただ,この資料で扱っている範囲の内容であれば
lme4パッケージでもほとんど同じ結果が得られます。そのため,使用している関数名を読み替えてしまえば,lme4パッケージの結果として読み進めてもなんの問題もありません。↩︎他に使用されることが多い(増えてきた)パッケージとしては,
brmsなどもあります。ただしbrmsパッケージはベイズ統計に基づく方法なので,結果を正しく理解するためにはまずはベイズ統計の勉強が必要となります。本Chapterでは説明していませんが,実は階層線形モデルはベイズ統計の事前分布の考え方と非常に相性が良いので,マルチレベルモデルを多用する場合には,こちらを検討しても良いかもしれません。↩︎厳密に言えば,ある生徒はある学校の中のあるクラスに所属しているので,データには3つの階層があると言えます。ただしPISAの場合,基本的に1つの学校からは1クラスだけが抽出されているようなので,2階層と考えてOKです。↩︎
詳細には,左は\(N(570, 70^2)\),右は\(N(430, 70^2)\)と設定しています。↩︎
具体的には,標本分布を使用して行う区間推定の幅を過度に小さく見積もってしまったり,統計的仮説検定において第一種の過誤の確率が有意水準\(\alpha\)よりも大きくなってしまいます。↩︎
一般的には,階層データに対する添字は\(i, j\)が使われるのですが,本資料では前のChapterとの一貫性から\(p(, g)\)を使用します。↩︎
要因数が複数であったり,混合計画(被験者間要因と被験者内要因が両方ある場合)では,
aov()関数は非対応とされています。このような場合,Rならばafexやrstatixといったパッケージを使うと良いでしょう。↩︎実際にやるとしたら,まず回帰分析によって\(\beta_{0g}\)を推定し,得られた集団レベルの推定値を被説明変数とした回帰分析を改めて実行する,という感じになると思います。ただこの場合,\(\beta_{0g}\)の推定の精度(サンプルサイズに基づく誤差)が無視されてしまうことが問題となります。↩︎
別にどのように表記しても良いのですが,一般的なマルチレベルの文献に少しでも近い表現にしておきます。気持ちの問題ですが。↩︎
もちろん,「家庭での運動を推奨する」程度などが学校レベルの施策として規定されるならば,「運動の頻度」を対象とした分析であってもマルチレベルモデルが必要になる可能性はあります。↩︎
ただし実際には\(\beta_{0g}\)の具体的な値を求める必要はないので,この式を変量効果パラメータ\(\beta_{0g}\)について積分(周辺化)したものを最大化することになります。↩︎
ちなみにここでは,恣意的に「
school_id == "001"の中でread_scoreが最も高かった3人」を選んでいます。↩︎必ず回帰係数が大きくなるとも限らないのですが,そうなることが多いと考えられます。その理由は,例えば文脈効果(もともと優秀な人が同じ学校に集まり,更にその学校で成長していく)や,相関の希薄化(平均値レベルでは,個人の測定値に含まれる誤差が相殺されるようになる)などが考えられます。↩︎
\(\sigma_{(0g)(\mathrm{ESCS},g)} = \rho_{(0g)(\mathrm{ESCS},g)}\sigma_{0g}\sigma_{\mathrm{ESCS},g}\)で求められます。↩︎
他にも,
interactionsパッケージなどは使いやすいパッケージなのですが,glmmTMB()関数の出力に一部非対応なため,modelbasedパッケージをメインに紹介します。↩︎sch_escs_meanがさらに大きくなると,傾きがほとんど変わらないどころか徐々に大きくなるにもかかわらず有意でなくなってしまいます。その理由は,そこまでsch_escs_meanが大きい学校が無いために,傾きの推定値の標準誤差(塗りつぶされている部分の幅)が大きくなっていくためです。↩︎ただ,
lmer()関数で推定すると問題ない推定値が得られます。したがって,推定のアルゴリズムの細かい違いによって結果がかなり変動してしまうほど推定が難しい(不安定)のかもしれません。glmmTMB()関数でうまく推定できたら教えて下さい。↩︎ここで正確な尤度を用いるので,
lme4::lmer()関数の場合にはREML = FALSEでモデルを実行しておく必要があったのです。↩︎model1はmodel3にネストしているとは言えません。またmodel4およびmodel7は別の変数s_t_ratioを使用しているため,ネストの関係にはありません。model5はmodel6にはネストしているものの,model3を内包していないため,ここでは除外します。↩︎どうやら
glmmTMB()の出力に対しては,そもそもネストの関係にないモデルを入れるとエラーが出てしまうようです。↩︎GLMに混合効果(mixed effects)モデルが組み合わさっていることから,GLMM (generalized linear mixed model)という略称も広く知られています。↩︎
ポアソン回帰の場合には,\(y_{pg}\)の分布はポアソン分布であり,平均と分散が等しいことから,レベル1の変量効果を考えることができません。↩︎
それでも,50%区間は\([0.612, 0.920]\)と,けっこう広い範囲になってしまいます。進学希望率はそれくらいピンキリということなのでしょう。↩︎
もちろん,この仮定はあくまでも「ロジスティック回帰分析においては」成り立つものです。同様にプロビット回帰の場合には,背後の連続量に標準正規分布を仮定するため,レベル1変量効果の分散は1と考えられます。↩︎
もしもっと複雑なモデリングができるならば,例えばまず「\(y_{pg}\)が全員0」「\(y_{pg}\)が全員1」「それ以外」の3つのグループに分けて,それぞれに対して別々のモデルを当てはめたり,どのグループに含まれるかを別の説明変数で回帰する,という方法も考えられるかもしれません。↩︎
別の対策としては,ベイズ推定を用いて,事前分布を設定するというやり方もあります。これは,
brmsなどのパッケージを用いると実行可能ですが,まずベイズ統計を勉強しないといけないのでここでは省略します。↩︎自分では何も思いつかなかったのでGeminiに聞いてみたところ,「 同じくらいの平均ESCSを持つ学校でも、一方は『全ての生徒に高い学力を要求し、進学を強く推奨する』という指導文化が教師陣全体で共有されているかもしれません。このような『高い期待をかける文化』という観測されていない要因は、生徒全体の進学意識を底上げします(切片を高くする)。しかし同時に、その高い要求に応えるための準備(学習習慣、文化資本)ができている高ESCSの生徒がより有利になり、結果として校内格差を広げてしまう(傾きを急にする)可能性があります。」といった可能性が考えられるそうです。信じるか信じないかはあなた次第です。↩︎
もちろん回帰係数は相関係数だけで決まるわけではないので,必ず「相関係数が高いほうが傾きも大きい」とは限らないのですが,もとが同じ変数(
escs)である以上,多くの場合にはこの傾向が言えるのではないかと思います。↩︎両レベルをまとめて推定した場合と,パラメータの推定値が若干ずれているので,もしかしたらレベルごとの適合度もあくまで近似的なものになっている可能性があります(未確認)。↩︎
group列は,多母集団同時分析での各集団の番号を表す列です。ちなみに,多母集団同時分析とマルチレベルSEMは,集団の違いを固定効果とみなすか変量効果とみなすか,が違うだけで位置づけとしては近い手法です。そのため,マルチレベル多母集団同時分析なんて方法(e.g., 学校×性別による違いの分析)も可能です。block列は,groupとlevelの両方を同時に区別するための列なので,マルチレベルSEMの場合にはlevelと同じ値に,多母集団同時分析の場合にはgroupと同じ値になります。マルチレベル多母集団同時分析になるとgroup数×level数の値が入ることになるようです。↩︎これも
lavaanの開発計画には”two-level SEM with random slopes”とあるので,いつかは実装されるのかもしれません。↩︎この考え方は,実は本節の前半で紹介したものとも共通しています。共通因子\(\beta_{0g}\)の分散が「(個人レベルの要素を完全に排除した)集団レベルの分散」に相当し,\(u_{pg}\)の分散が「個人レベルの分散」となるのです。↩︎
tidyverseな方法で言えばpivot_wider()などを使うのが良いかもしれませんが,本資料ではあえてtidyverseに頼らないことにしています。↩︎