研究テーマ3.
テラヘルツ電磁波による凝縮相の低振動スペクトル
分子性結晶のテラヘルツスペクトルとその同定
分子性結晶の中で、ナフタレンやアントラセンなどの結晶は、水素結合など分子間相互作用の中でも比較的強い相互作用で結晶を構成しているわけではない。テラヘルツスペクトルには、分子内振動の大振幅振動であるバタフライ運動が非常に大きな赤外強度を持って観測される。この振動モードが分子内のモードとしては、最低振動数のものである。さらにその低波数側に格子振動と思われる弱いバンドが観測される。このような分子性結晶ではモードの同定はそれほど困難ではない。しかし、水素結合性の分子になると、一般には200 cm-1に複数の振動バンドが観測される[1]。それらのバンドに対して近年分子軌道法を用いた計算や単位格子を考慮した計算などが行なわれているが、振動モードの同定は決して十分レベルにあるとはいえない。我々はこの水素結合性分子のテラヘルツ帯のバンドに対する同定に関して、以下のアプローチにより研究を進めている。
1) 測定は5 Kなど、極低温で行なう。常温298 Kは波数で207 cm-1に相当するため、低振動モードを常温で測定すると、v=0→v=1の遷移以外に、v=1→v=2, v=2→v=3等のホットバンドが重なる。試料の温度を低温に下げると、一般にはバンドが狭線化し、高振動数側へピーク位置がシフトする。これは温度変化による結晶構造の変化も寄与しているが、主には振動モードの非調和性から生じていると考えることができる。そのため、測定は極低温で行い、v=0→v=1の遷移だけを観測するようにする。
2) 同位体を合成し、同位体シフトを観測する。これは中赤外領域の赤外分光やラマン散乱分光にて振動モードの同定で行なわれてきた手法であり、通常、HをD、16Oを18O、14Nを15Nなどに置換し、換算質量の変化による振動バンドのシフトを観測する。本研究では、カルボキシル基のHをDに置換して同位体シフトを観測した。
3) 結晶構造の周期性を取り入れた分子軌道法を用いて、同位体置換された分子と通常の分子(H体)について構造最適化と基準振動解析を行ない、振動モードの振動数を求め同位体シフトを評価する。構造最適化を行なう際、結晶構造が必要であるが、X線回折実験から求まった構造を入力し、構造最適化を行なう。その結果、最終的な構造が最初に入力したものとそれほど異ならないことを確認する。計算にはCRYSTAL06コードを用いた。この手法では、ガウス型の原子軌道を扱い、孤立分子の分子軌道計算に一般に使われているGAUSSIAN06の分子性結晶への拡張版である。これに対して、平面波の線形結合を基底関数として用いる方法があり、VASPなどのプログラムがテラヘルツ帯のスペクトルの解析に用いられている[2,3]。文献4が平面波とガウス型の軌道を使う手法に関する比較について詳しく述べている。
4) 以上、実験的、理論的にバンドの振動数と同位体シフトを求め、それらを比較することにより振動モードの同定を行なう。上でも述べたが、この方法は中赤外領域の振動分光で通常行なわれているバンドの同定方法と同じものである。
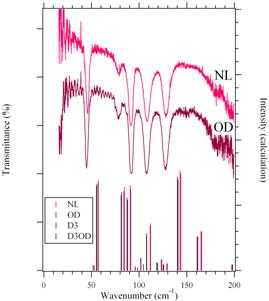 |
| 図1.2-フランカルボン酸のテラヘルツスペクトルの測定結果(上)と計算結果(下) |
図1に2?フランカルボン酸の透過スペクトルの結果を示す。測定は5 Kで行い、時間領域法ではなく、単色コヒーレント光を用いた手法で行なっている。NLがH体、ODがカルボキシル基の水素を重水素化したものである。表1に各バンドの振動数と同位体シフトをまとめる。S/N比は十分でないが、180 cm-1付近にH体、OD体、ともにバンドが存在することがわかる。図中の棒グラフはCRYSTAL06で計算した結果であり、基底関数として6-31++G(d,p)を、B3LYP複合型汎関数を用いている。計算はH体とOD体以外に、五員環の3つの水素原子を重水素化したD3と全ての水素原子を重水素化したD3ODの計算結果も載せてある。H体とOD体の振動数と同位体シフトの計算結果を表2にまとめる。H体の赤外強度もあわせて示す。ここでは赤外強度が比較的大きい6つのバンドを選んだ。スペクトル測定では、バンド3が負の同位体シフトを示すが、これは実験誤差であると思われる。計算で求めた振動数は実験値を大まかには再現していると思われる。同位体シフトの大きさも実験、計算ともに1cm-1以下であり、オーダー的には一致している。しかし、実験では、最低振動数のバンド1がもっとも大きな同位体シフトを示したのに対して、計算では最低振動数のバンド1がもっとも同位体シフトが小さい。実験と計算の違いの原因としては、(1)計算ではポテンシャルを調和振動子と近似して、振動数を求めているが、低振動モードは一般的には非調和性が強く、調和振動子と近似することは無理があるかもしれない。振動モードの非調和性を調べるためには、テラヘルツスペクトル測定とX線回折測定による結晶構造解析の温度変化を調べ、それぞれの温度でCRYSTAL06による計算を行なうことが一つの可能性である。(2)計算手法それ自身の問題をあげることができる。分子間相互作用のように非常に弱い相互作用を正確に取り入れていくことは今後の理論計算の大きな課題であり、例えば、分散力のような相互作用をどのような形で取り入れていくか、検討が必要である。
以上のように、現状ではまだバンドの振動数だけでなく、その同位体シフトを、完全に再現することはできていない。我々の測定結果が、理論計算の一つの標準となり、今後、水素結合や分子間相互作用の理論計算が向上することが期待される。
本研究は、神原大博士(神戸大)、西澤潤一教授(上智大)、佐々木哲朗准教授(上智大)、Hong-Wei Wang博士(台湾国立大)、林倫年教授(台湾国立大)との共同研究である。
| バンドの番号 | n(NL)/ cm-1 | n(OD)/ cm-1 | n(NL)-n(OD)/ cm-1 |
|---|---|---|---|
| 1 | 45.8 | 45.1 | 0.7 |
| 2 | 78.8 | 78.6 | 0.2 |
| 3 | 91.3 | 91.7 | -0.4 |
| 4 | 108.4 | 108.0 | 0.4 |
| 5 | 128.2 | 127.8 | 0.4 |
| バンドの番号 | n(NL)/ cm-1 | 赤外強度/ km/mol | n(OD)/ cm-1 | n(NL)-n(OD)/ cm-1 |
|---|---|---|---|---|
| 1 | 57.22 | 6.91 | 56.89 | 0.33 |
| 2 | 84.46 | 6.39 | 83.93 | 0.53 |
| 3 | 91.20 | 6.21 | 90.62 | 0.58 |
| 4 | 112.03 | 3.60 | 111.61 | 0.42 |
| 5 | 143.67 | 7.39 | 142.89 | 0.78 |
| 6 | 165.60 | 2.97 | 164.89 | 0.71 |
参考文献
- K. Yamamoto, Md. H. Kabir, and K. Tominaga, J. Opt. Soc. Am. B 22, 2417 (2005).
- S. Saito, T. M. Inerbaev, H. Mizuseki, N. Igarashi, R. Note, and Y. Kawazoe, Chem. Phys. Lett. 432, 157 (2006).
- P. Uhd Jepsen and S. J. Clark, Chem. Phys. Lett. 442, 275 (2007).
- S. Tosoni, C. Tuma, and P. Ugliengo, J. Chem. Phys. 127, 154102 (2007).

