研究テーマ1.
赤外非線形分光(3-パルスフォトンエコー法)による振動状態の揺らぎの観測
赤外非線形分光法による水溶液中での溶質の振動ダイナミクスの温度変化
石原 茜衣,田山 純平,伴野 元洋,太田 薫,富永 圭介
[第3回分子科学討論会にて発表。その予稿を改編]
【序】
溶液中において溶質分子は周囲の溶媒分子から揺動を受けており,溶質の電子遷移や振動遷移の遷移振動数は時々刻々変化している.特に水中では水素結合の生成と解離による特異なダイナミクスが存在し,溶質の振動数の揺らぎが水溶液中における化学反応やタンパク質の機能発現にも重要な役割を果たしていると考えられる.3次の光学非線形分光法である赤外3パルスフォトンエコー法を用いると分子振動の振動数揺らぎについての詳細な情報を得ることができる.本研究では比較的単純な構造をもつイオンであるアジドを溶質に選び,重水中におけるアジドの反対称伸縮振動の振動数揺らぎを赤外3パルスフォトンエコー法により調べた.3パルスフォトンエコー信号の詳細な解析には分布緩和や回転緩和に関する情報が必要であり,それらを偏光分解赤外ポンプ‐プローブ分光法により求めた.特に振動数揺らぎを支配している溶質‐溶媒相互作用や溶媒のダイナミクス等を理解するために,揺らぎの時間相関関数の温度依存性を調べてその機構について検討した.
【実験】
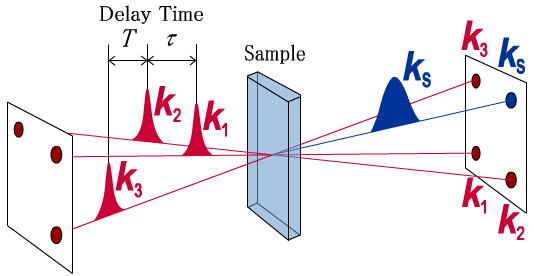 |
| 図1 パルス配置とシグナルの検出位置,および遅延時間T,τの定義 |
赤外3パルスフォトンエコー法および偏光分解赤外ポンプ‐プローブ分光法では,自作の光パラメトリック増幅器により発生させた二色の近赤外光の差周波をとることにより得られた中赤外パルスを用いた.赤外3パルスフォトンエコー法では図1に示すように3つの赤外パルスを異なる方向から試料に入射し,位相整合条件(ks = - k1 + k2 + k3)を満足する方向にフォトンエコー信号を得た.ここで,第2パルスの第1パルスからの遅延時間をτ,第3パルスの第2パルスからの遅延時間をTと定義し,測定ではτとTをそれぞれ変化させながらフォトンエコー信号を観測した.偏光分解赤外ポンプ‐プローブ分光法では,赤外パルスを2つに分けてポンプ光およびプローブ光として用いた.
【結果と考察】
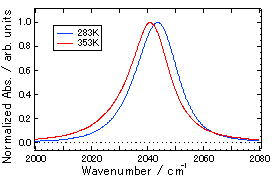 |
| 図2 重水中におけるN3-の反対称伸縮振動モードの赤外吸収スペクトルの温度変化 |
重水中のアジドの反対称伸縮振動バンドは2040 cm-1付近にピークを持つ.図2に示すように,温度が上昇するに伴ってピーク位置は低波数側へシフトした.一般に,アジドの反対称伸縮振動のピーク位置は非水素結合性溶媒中では水素結合性溶媒中よりも低波数側に現れる.観測された低波数シフトは温度上昇に伴い,溶媒分子の運動が激しくなり平均的にみて水素結合が弱くなったと考えられる.
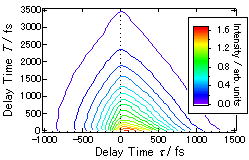
図3に重水中でのアジドの赤外3パルスフォトンエコー信号を示す.T = 0でのフォトンエコー信号のピークはτ = 0からずれており,これは遷移振動数の分布に過渡的な不均一性が存在することを示している.これを定量的に評価するため,各Tでの一次モーメントを求め,Tに対してプロットした(図4). この一次モーメントのT依存性は近似的に遷移振動数揺らぎの時間相関関数に比例することが知られている.これを単一指数関数でフィットすると,減衰の時定数は293, 313, 333, 353 Kでそれぞれ1.6, 1.3, 1.2, 1.1 psと求められ,温度が上昇するに伴って減衰が速くなることが分かった.
 |
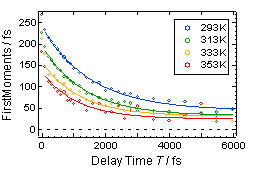 |
| 図3 重水中のN3-のフォトンエコー信号 | 図4 フォトンエコー信号の一次モーメントの温度変化 |
続いて偏光分解赤外ポンプ‐プローブ信号の解析から得られた回転緩和および分布緩和の時定数を用い,フォトンエコー信号および赤外吸収スペクトルの数値シミュレーションを行った.遷移振動数揺らぎの時間相関関数には式(1)のような二つの指数関数と定数項の線形結合を仮定し,含まれるパラメータを最適化した.
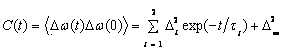
各温度における相関関数のパラメータを表1に示す.温度上昇に伴って時定数は小さくなり,遅い成分の相対的な強度が小さくなった.揺らぎの時定数は溶質の周辺環境の時間変化,つまり溶媒和ダイナミクスのタイムスケールに相当することから,温度上昇に伴い系の溶媒和ダイナミクスが速くなったと考えられる.それぞれの揺らぎ成分が溶液中のどのようなダイナミクスに由来するものかを考察するため,水の動的性質を表す物理量の温度依存性と比較した.例えば, ここで得られた時定数の温度依存性と重水のデバイ緩和時間の温度依存性1とを比較すると明らかに異なっていることから,この振動数揺らぎはピコ秒の時定数を持つ誘電緩和の成分によるものではないと考えられる.
| 温度/K | Δ1/ps-1 | τ1/ps | Δ2/ps-1 | τ2/ps | Δ∞/ps-1 |
|---|---|---|---|---|---|
| 283 | 2.5 | 0.11 | 1.2 | 1.4 | 0.3 |
| 293 | 2.6 | 0.10 | 1.1 | 1.3 | 0.4 |
| 313 | 2.8 | 0.10 | 1.0 | 1.3 | 0.4 |
| 333 | 2.8 | 0.08 | 1.0 | 1.2 | 0.4 |
| 353 | 3.0 | 0.08 | 0.9 | 1.1 | 0.4 |

