Estimation of Hydraulic Conductivity of a Leaky Aquifer System from Observed Drawdowns
Masahiko Saito 1 , Takeshi Kawatani 2
ABSTRACT
It is important to evaluate the hydraulic conductivity of a semiconfining stratum of leaky aquifer system. In the case where the confining layer is semipervious, the deep well operation for a large-scale excavation may fail to achieve the expected result and affects the flow and transport process not only in the pumped aquifer but also in neighboring aquifers. However, the field measurement method such as a pumping test is not applicable directly to a semipervious layer because of its low permeability.
The objective of this study is to develop the method of inverse analysis for identification of the regional hydraulic conductivity of semiconfining layer as well as the conductivity of aquifers in a leaky aquifer system. The inverse analysis in this study is based on a finite element method and a constrained simplex method. The finite element formulation is carried out based on the governing equations for quasi-3D flow in which the flow in the aquifers is horizontal and that in the semiconfining layer is vertical.
The inverse analysis is performed employing the drawdown data obtained in the large excavation site (400m x 100m). A set of drawdown data was obtained by pumping test prior to the excavation and the other set was observed in 11 observation wells during the deep well operation. The former set was used to identify the conductivity of a semicofining layer and two aquifers by the analysis of axisymmetric flow. The latter was employed both for the quasi-3D analysis and for the horizontal 2D analysis of the flow in the lower aquifer whose confining layer was assumed to be impervious.
The quasi-3D analysis resulted in the best matching of observed and calculated drawdowns. This indicates that the quasi-3D analysis is useful to identify the hydraulic conductivity of not only the aquifers but the semipervious confining layer from the observed drawdowns. This method is also suitable to find out the heterogeneity in aquifers. It is concluded that the method proposed in this study is useful tool for identifying regional hydraulic characteristics of leaky aquifer system and for obtaining its more realistic view.
1 Introduction
The deep well operation is often carried out to prevent the heaving of the layer of low permeability in large-scale excavation site. At the stage of designing the operation, it is common to assume that the layer subject to the heaving is an impervious confining layer. However, since in reality the layer is more or less pervious, the pumping from the underlying aquifer induces the leakage from the neighboring aquifers through the semipervious layer. Thus, the deep well operation may fail to achieve the drawdown of piezometric head intended in the design and affects the flow and transport process not only in the pumped aquifer but also in the neighboring aquifers. Therefore, it is necessary to know the regional hydraulic conductivity of the semiconfining layer for reliable design of the operation and proper management of ground water during the excavation work. However, the direct measurement of the hydraulic conductivity of the semiconfining layer by a pump test is practically impossible because the conductivity is too low.
This study aims at developing the method of inverse analysis to evaluate the regional hydraulic conductivity of the semiconfining layer as well as the conductivity of aquifers in a leaky aquifer system. In order to investigate the applicability of this method, the inverse analysis is performed employing the drawdown data obtained in the large excavation site of 400m x 100m.
2 Methodology
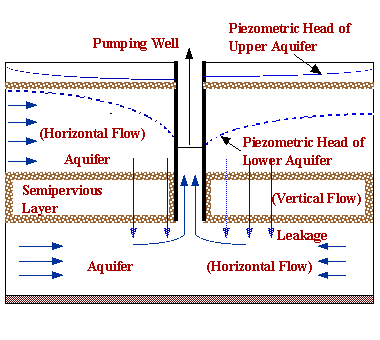
Figure 1 Leaky Aquifer System
Figure 1 illustrates the leaky aquifer system simulated herein. A semipervious confining layer lies between two aquifers. The upper aquifer may be confined or unconfined. When the difference in piezometric head is created across the semipervious layer by pumping from the lower aquifer, the leakage from the upper aquifer to the lower occurs.
The inverse analysis in this study consists of the finite element analysis of flow and the constrained simplex method for parameter identification. For the analysis of the flow, both axisymmetric and quasi-three dimensional simulation models were employed. Of course the former is applicable only to axisymmetric flow field including the boundary condition. Hence, the inverse analysis based on the axisymmetric model was applied when employing the data obtained by the pump test prior to the excavation work. On the other hand, the quasi-3D model [1], [2] in which the flow is presumed to be horizontal in the aquifers and vertical in the semipervious layer can deal with the heterogeneity of both boundary conditions and conductivity. Thus, the quasi-3D simulation was applied to the inverse analysis when the data measured during the excavation work were utilized.
The constrained simplex method [3], [4] is used to determine the most probable values of hydraulic conductivity and specific storativity from the field observation data of piezometric head. The objective function defined in this analysis is
![]()
Where ho(n) and hc(n) denote the observed and calculated piezometric heads in the n-th observation well, respectively, and m is the number of the observation wells. The convergence of the apexes of simplex to the optimum point is achieved when the standard deviation of the objective functions calculated at all apexes becomes less than a certain criterion. Then, the average of the coordinates of apex provides the most probable parameters.
3 Study Area and Field Data
Figure 2 illustrates the excavation site of 400m x 100m and the locations of the pumping and observation wells. The three of the observation wells are located inside the excavation area. Figure 3 shows the formation at the excavation site which is divided into five strata. The first, third and fifth strata from the top are aquifers while the second and fourth strata are aquitard or aquiclude which is semipervious. The excavation area is surrounded by a soil-cement mixing wall (SMW) which is impervious and reaches down to the top of the fifth stratum, i.e., the pumped aquifer. The initial piezometric heads in the three aquifers are nearly the same. The bottom three strata are the object of this inverse analysis.
Figure 2 The Excavation Site
Figure 3 Formation at the Excavation Site
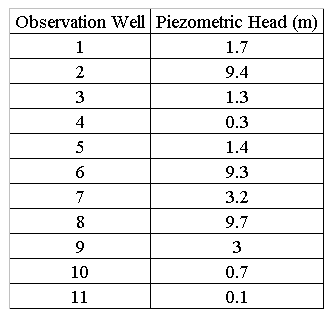
Two sets of data of the piezometric head in the bottom aquifer, i.e., the fifth stratum are available for the inverse analysis. One set was obtained at three observation wells by performing the pump test at the rate of 0.25 m3/min prior to the deep well operation. The distances between the pumping well and the three observation wells are 5 m, 20 m and 50 m, respectively. Figure 4 presents the results of the pump test. The other set was measured at eleven observation wells three months later after the deep well operation started. The operation was conducted at four wells located in the northern part of the site. The pump-up rate of each well was about 0.7 m3/min. The observed piezometric heads are given in Table 1.
Figure 4 Pump Test
Table 1 Observed Piezometric Heads
4 Inverse Analysis by Axisymmetric Simulation
In this analysis, the specific storativity was estimated besides the conductivity because the pump test provided the temporal changes of piezometric head. However, it was assumed that the storativity of both aquifers was the same. To examine whether or not the initial values of the parameters affected the results, five realizations were performed producing the initial values by a random generator.
The results are given in Table 2 where k3 and k5 are the conductivity of the upper and lower aquifers, respectively, k4 is the conductivity of the semipervious layer, S3 and S5 are the storativity of the upper and lower aquifers, respectively, S4 is the storativity of the semipervious layer. The conductivity of the lower aquifer is about 9x10-3 cm/s in all realizations. Meanwhile, the conductivity of the upper aquifer ranges approximately from 5x10-4 to 2x10-1 cm/s. The uncertainty of the k3 estimation might be resulted from the fact that the period of the pump test was too short for the leakage to develop and affect the piezometric head of the lower aquifer. The values of the objective function are nearly the same in all runs. These results indicate that the accuracy of the estimation depends mainly on the conductivity k5 but little on the conductivity k3. The conductivity of the semipervious layer is estimated at about 7x10-6 cm/s though it ranges from 3x10-6 cm/s to 1.4x10-5 cm/s. The estimated storativity of the aquifer and that of the semipervious layer seem to be acceptable because they lie within the range of storativity for sandy stratum and clayey layer, respectively.
5 Inverse Analysis by Quasi-3D Simulation
In this analysis, the flow was assumed to be steady when the piezometric heads were measured because the pump test was implemented three months later after the deep well operation started. Hence, the conductivity was estimated but not the storativity. It was also assumed that the conductivity of the northern half of the lower aquifer (k5n) was different from that of the southern half (k5s). The constraint was that the lower bound of the conductivity was 1.67x10-4 cm/s in the aquifers and 1.67x10-8 cm/s in the semipervious layer. In addition to the quasi-3D simulation, a plane 2D simulation in which no leakage was assumed was carried out to estimate only the conductivity of the lower aquifer.
The estimated conductivity is presented in Table 3. In the case of the quasi-3D simulation, the estimated k5n of 7.46 cm/s is almost the same as the value estimated in the axisymmetric simulation. Meanwhile, the estimated value of k5s turned out to be the lower bound of the aquifer conductivity. This suggests that the conductivity is quite low in the southern half of the lower aquifer. The value of k4 is about six times larger than the value obtained by the axisymmetric simulation. Although it is hard to tell which result is more reliable, it is noted that the quasi-3D analysis takes account of both the heterogeneity and the impervious SMW surrounding the excavation site. The value of k5n estimated by 2D analysis is nearly four times larger than the value identified by the quasi-3D analysis. This is accounted for as follows. Since no water flows into the lower aquifer through the overlying confining layer in the 2D analysis, the conductivity needs to be large to supply the amount of water pumped up from the deep wells for the sake of satisfying the continuity equation. The k3 estimated by the quasi-3D analysis is approximately 10-1 cm/s. This relatively high conductivity indicates that the large amount of water leaks out of the upper aquifer into the lower aquifer.
Table 3 Estimated Conductivity
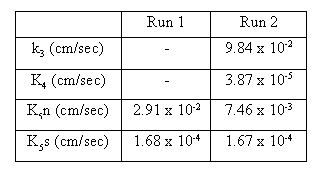
Figure 5 Differences Between Observed and Calculated Head
Figure 6 Distributions of Calculated Piezometric Head
6 Conclusions
A quasi-3D simulation in which the flow was assumed to be horizontal in aquifers and vertical in a semipervious layer has been performed to estimate not only the hydraulic conductivity of aquifers but also that of the smipervious layer in a leaky aquifer system. The inverse analysis based on the quasi-3D model was applied to a large-scale excavation site where deep well operation was conducted. This method could take into account the effect of the impervious wall surrounding the site on the flow. The analysis resulted in good matching of observed and calculated drawdowns and provided good estimation of the hydraulic conductivity of the semipervious layer. It is concluded from these results that the method of inverse analysis described in this paper is useful tool for estimating regional hydraulic characteristics of leaky aquifer system and for obtaining its more realistic view.
References
[1] Chorley, D. W. ; Frind, E. O.
An iterative quasi-three dimensional finite element model for heterogeneous multiaquifer systems, Water Resources Research, 14(5), 943-952, 1978
[2] Kawatani, T. ; Saito, M. ; Tsuchiyama, J.
Inverse analysis of estimating permeability of semipervious confining layer, Proceedings of the 27th Congress of IAHR: Groundwater, 45-50, 1997
[3] Box, M. J.
A new method of constrained optimization and a comparison with other methods, Computer. J., 8, 452, 1965
[4] Reklaitis, G. V.
Engineering Optimization, Methods, and Applications, John Wiley, p.684, 1983
1. Research Associate, Department of Architecture and Civil Engineering,
Kobe University, Nada, Kobe 657-8501, Japan
2. Professor, Research Center for Urban Safety and Security,
Kobe University, Nada, Kobe 657-8501, Japan